帶單個(gè)變點(diǎn)AR(1)模型的統(tǒng)計(jì)推斷
楊 磊, 楊蘭軍,, 吳劉倉
(1.昆明理工大學(xué)理學(xué)院,昆明 650500; 2.昆明理工大學(xué)應(yīng)用統(tǒng)計(jì)學(xué)研究中心,昆明 650500)
0 引言
為方便討論,本文常用記號規(guī)定如下:對于方陣A,tr(A)、AT、(A)i和rank(A)分別表示A的跡、A的轉(zhuǎn)置、A的第i個(gè)主對角元素和A的秩;A-代表A的廣義逆,即滿足AA-1A=A;In表示n階單位陣,1n表示元素都是1 的n維列向量,en(i)為第i個(gè)元素為1 其他元素為0 的n維列向量;a= arga∈Λ{F}表示a取集合Λ內(nèi)滿足屬性F的值;Eθ0(·)和Dθ0(·)分別表示在模型參數(shù)取θ0條件下求期望與方差;o(1)和O(1)分別表示無窮小量和一致有界量;oP(1)和OP(1)分別表示依概率收斂到0 和依概率一致有界;P-→和d-→分別表示依概率收斂和依分布收斂。
時(shí)間序列模型一直都是統(tǒng)計(jì)學(xué)家研究的焦點(diǎn)和重點(diǎn),但由于問題的復(fù)雜性,簡單的時(shí)間序列模型往往不足以解決現(xiàn)實(shí)問題。當(dāng)模型結(jié)構(gòu)發(fā)生變化時(shí),變點(diǎn)時(shí)間序列往往成為關(guān)注點(diǎn)之一。變點(diǎn)問題的處理方法在不斷發(fā)展,在經(jīng)典方法中,Hinkley[1]通過累積和(Cumulative Sum,CUSUM)方法研究了正態(tài)分布的均值結(jié)構(gòu)變點(diǎn)問題;Brown 等[2]提出了累計(jì)平方和方法研究時(shí)間序列的方差變點(diǎn)問題;Incl′an 和Tiao[3]在Brown 等的基礎(chǔ)上提出了迭代累積平方和方法用于檢測獨(dú)立隨機(jī)序列的變點(diǎn)問題;Horv′ath[4]通過極限理論研究了自回歸模型中變點(diǎn)的極大似然估計(jì)問題;Bai[5]基于最小二乘方法研究了線性過程的均值變點(diǎn)問題,得到了變點(diǎn)估計(jì)量的漸近分布;Galeano 和Pe?na[6]通過CUSUM 方法研究了向量ARMA 模型在小樣本下的方差變點(diǎn)檢測問題;Liu 等[7]通過經(jīng)驗(yàn)似然比方法研究了線性回歸模型中的結(jié)構(gòu)變點(diǎn)問題;Xia 等[8]通過加權(quán)殘差的累計(jì)和方法以及移動和方法對廣義線性模型進(jìn)行了變點(diǎn)檢測,考慮了檢驗(yàn)統(tǒng)計(jì)量的漸近分布問題;Berkes 等[9]通過似然比檢驗(yàn)研究了門限AR(1)模型的結(jié)構(gòu)變點(diǎn)問題;Pang 等[10]研究了平穩(wěn)和近似平穩(wěn)情形下帶有變點(diǎn)的AR(1)模型的漸近理論;Xia 和Qiu[11]提出了一種跳躍信息準(zhǔn)則用于估計(jì)帶有未知跳躍點(diǎn)的非連續(xù)曲線;譚智平和繆柏其[12]通過Kolmogorow 型統(tǒng)計(jì)量對連續(xù)隨機(jī)變量的變點(diǎn)位置進(jìn)行了檢測;李訂芳等[13]通過基于小波包的探測算法研究了時(shí)間序列變點(diǎn)問題;趙文芝和夏志明[14]基于加權(quán)殘差的CUSUM 方法研究了線性模型漸變變點(diǎn)的檢驗(yàn)問題。基于貝葉斯思想來研究時(shí)間序列變點(diǎn)問題的方法也得到了發(fā)展,McCulloch 和Tsay[15]利用Gibbs 抽樣理論研究了均值和方差變點(diǎn)的自回歸模型的統(tǒng)計(jì)推斷問題;Chen 等[16]在貝葉斯框架下提出一種對雙線性時(shí)序模型的變點(diǎn)檢測算法;Slama 和Saggou[17]通過貝葉斯顯著性檢驗(yàn)研究了自回歸模型的方差突變問題;熊立華等[18]通過貝葉斯方法,結(jié)合MCMC 抽樣理論對水文時(shí)間序列的均值突變進(jìn)行了研究。
目前大量的文獻(xiàn)主要集中在對時(shí)間序列均值或方差變點(diǎn)問題的研究,對于回歸函數(shù)參數(shù)變點(diǎn)問題的研究則相對較少,其中Chong[19]的研究特別值得關(guān)注。該文獻(xiàn)就帶有單個(gè)變點(diǎn)的AR(1)模型,基于最小二乘估計(jì)討論了自相關(guān)系數(shù)估計(jì)量的相合性和極限分布。不同的背景和不同的研究方法可能得到不同的研究結(jié)果。本文主要考慮帶單個(gè)變點(diǎn)AR(1)模型基于極大似然估計(jì)(Maximum Likelihood Estimate, MLE)或擬似然估計(jì)(Quasi-Maximum Likelihood Estimate, QMLE)的統(tǒng)計(jì)特征,主要包括三個(gè)方面:
1) 討論了模型參數(shù)的MLE(或QMLE)及估計(jì)的存在性問題;
2) 討論了自相關(guān)系數(shù)的MLE(或QMLE)的大樣本特征;
3) 討論了存在單個(gè)變點(diǎn)的自相關(guān)系數(shù)簡單假設(shè)檢驗(yàn)問題。
本文安排如下:第1 節(jié)討論帶單個(gè)變點(diǎn)AR(1)模型參數(shù)MLE(或QMLE)的表達(dá)形式及其存在性問題,給出了自相關(guān)系數(shù)MLE(或QMLE)的一致性和漸近正態(tài)分布結(jié)果,對關(guān)于變點(diǎn)前后的自相關(guān)系數(shù)ρ1、ρ2的假設(shè)H0:ρ2-ρ1=λ0的檢驗(yàn)問題進(jìn)行了討論;第2 節(jié)通過數(shù)值模擬論證了自相關(guān)系數(shù)的一致收斂性質(zhì),通過上證綜合指數(shù)日成交量數(shù)據(jù),論證了模型是否存在單變點(diǎn)情況的假設(shè)(H0:ρ2-ρ1= 0)檢驗(yàn)及自相關(guān)系數(shù)變化增量假設(shè)(H0:ρ2-ρ1=λ0)檢驗(yàn)的有效性與合理性;第3 節(jié)是本文的總結(jié)部分。
1 主要內(nèi)容
1.1 模型參數(shù)的極大似然(或擬似然)估計(jì)
本文考慮帶有單個(gè)變點(diǎn)的一階自回歸(First-order Autoregressive, 簡記AR(1))模型
其中E(X1) =μ/(1-ρ1), D(X1) =σ2/(1-ρ21),X1,ε1,···,εn-1為獨(dú)立隨機(jī)變量且存在常數(shù)γ>0,使得

從而,樣本的對數(shù)似然(或擬似然)函數(shù)為

由于ρ1∈(-1,1)時(shí),總有rank[B1(ρ1)]=n-q ≥1 且B1(ρ1)≥0,因而有P(XTB1(ρ1)·X>0)=1,即當(dāng)?ρ1存在且?ρ1∈(-1,1)時(shí),參數(shù)ρ2的估計(jì)為~ρ2(?ρ1)且以概率1 存在。將~ρ2(ρ1)代入~L(ρ1,ρ2),得到關(guān)于參數(shù)ρ1的中心化對數(shù)似然(或擬似然)函數(shù)為
由(3)式、(5)式和(6)式知,模型參數(shù)μ?、σ2、ρ2的極大似然(或擬似然)估計(jì)都與自相關(guān)系數(shù)ρ1密切相關(guān),ρ1的估計(jì)成為得到模型參數(shù)極大似然(或擬似然)估計(jì)的關(guān)鍵且該參數(shù)的估計(jì)可以通過極大化L(ρ1)得到。由于L(ρ1)比較復(fù)雜,關(guān)于ρ1的顯式解不易于獲取,因此自相關(guān)系數(shù)ρ1極大似然(或擬似然)估計(jì)的存在性和一致性等性質(zhì)的探討具有重要意義。
由于

引理1 當(dāng)q ≥1,n-q ≥1 且n ≥3 時(shí),我們有:
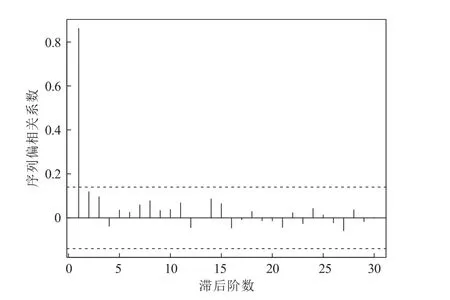
(i) 0 (ii) 0 證明 假定q ≥2,n-q ≥1,由于 類似地,記 則P(-∞ 因而,當(dāng)n ≥3 時(shí),有 類似地,可證當(dāng)q ≥1,n-q ≥1 且n ≥3 時(shí),以下結(jié)論成立。 引理2 當(dāng)q ≥1,n-q ≥1 且n ≥3 時(shí),我們有: (i)f(ρ1)關(guān)于ρ1在(-1,1)連續(xù); (ii) limρ1→1-f(ρ1)=∞, limρ1→-1+f(ρ1)=-∞幾乎處處成立。 證明 假定q ≥2,n-q ≥1,由于 以概率1 成立。 由引理1 及(9)式,可得f(ρ1),ρ1∈(-1,1)連續(xù),且limρ1→1-f(ρ1)=∞, limρ1→-1+f(ρ1)=-∞幾乎處處成立。 類似地,可證當(dāng)q ≥1,n-q ≥1 且n ≥3 時(shí),結(jié)論成立。 定理1 在模型(1)中,當(dāng)q ≥1,n-q ≥1 且n ≥3 時(shí),參數(shù)ρ1的極大似然(或擬似然)估計(jì)?ρ1以概率1 存在,且參數(shù)ρ1的極大似然(或擬似然)估計(jì)?ρ1為f(ρ1) = 0,ρ1∈(-1,1)的零點(diǎn)。 類似地,可證當(dāng)q ≥1,n-q ≥1 且n ≥3 時(shí),結(jié)論成立。 在模型(1)中,對于模型參數(shù)μ?、σ2、ρ1和ρ2的極大似然(或擬似然)估計(jì),有以下結(jié)論成立。 定理2 對于模型(1),參數(shù)μ?、σ2、ρ1和ρ2的極大似然(或擬似然)估計(jì)以概率1 存在的充分必要條件為q ≥1,n-q ≥1 且n ≥3,且模型參數(shù)的極大似然(或擬似然)估計(jì)?μ?、?σ2、?ρ1和?ρ2有如下表達(dá)形式 證明 由定理1 可知,若ρ1的極大似然(或擬似然)估計(jì)?ρ1存在且為f(ρ1) = 0,ρ1∈(-1,1)的零點(diǎn),則有引理1 和引理2 成立。又由引理1 可知,當(dāng)q ≥2,n-q ≥1 時(shí),有 故若引理1 成立,則有q ≥2,n-q ≥1 且n ≥3 成立。結(jié)合定理1,即有ρ1的極大似然(或擬似然)估計(jì)?ρ1存在的充分必要條件為q ≥2,n-q ≥1 且n ≥3。由于在此條件下,有P[~σ2(ρ1,~ρ2(ρ1))>0]=1,因此參數(shù)ρ1的極大似然(或擬似然)估計(jì)?ρ1以概率1 存在時(shí),模型參數(shù)μ?、σ2和ρ2的估計(jì)也以條件概率1 存在。 綜上,即有模型參數(shù)(μ?,σ2,ρ1,ρ2)極大似然(或擬似然)估計(jì)以概率1 存在的充分必要條件為q ≥2,n-q ≥1 且n ≥3。 在模型參數(shù)的估計(jì)中,(5)式表明?ρ2與參數(shù)ρ2的真實(shí)值ρ20有關(guān)。當(dāng)|ρ20|≥1 時(shí),并不能確保序列平穩(wěn),同時(shí)即使|ρ20|< 1,也不一定有|?ρ2|< 1。因此,當(dāng)|ρ20|<1 時(shí),?ρ2的一致收斂特征特別值得關(guān)注。 一致性研究是變點(diǎn)模型參數(shù)估計(jì)的一個(gè)重要部分。在|ρ2|< 1 和|ρ1|< 1 的條件下,下面討論參數(shù)ρ1、ρ2極大似然(或擬似然)估計(jì)的一致性問題。為方便討論,記p=n-q,模型參數(shù)θ的真實(shí)值θ0=(μ?0,σ20,ρ10,ρ20),以及函數(shù) 則關(guān)于參數(shù)ρ1、ρ2極大似然(或擬似然)估計(jì)的一致性有如下重要結(jié)論。 上面論述表明(13)式成立。類似地,可以證明當(dāng)q=1 且p →∞時(shí),結(jié)論成立。 綜上所述,結(jié)論成立[20]。 對于帶單個(gè)變點(diǎn)的時(shí)間序列模型,單個(gè)自相關(guān)系數(shù)估計(jì)的大樣本性質(zhì)值得關(guān)注,但是是否存在變點(diǎn)更值得關(guān)注。在自相關(guān)系數(shù)估計(jì)一致性條件下,下面重點(diǎn)考慮參數(shù)λ=ρ2-ρ1極大似然(或擬似然)估計(jì)的漸近分布。 假設(shè)模型參數(shù)真值ρ10∈(-1,1),ρ20∈(-1,1),則有以下的定理5。 證明 假定q ≥2,n-q ≥1,作參數(shù)變換λ=ρ2-ρ1,則關(guān)于參數(shù)ρ1和λ的中心化對數(shù)似然(或擬似然)函數(shù)(ρ1,λ),ρ1∈(-1,1),λ ∈(-2,2)為 則由定理5,有 其中 類似地,可以證明當(dāng)q=1 且p →∞時(shí),結(jié)論成立。 在定理5 和定理6 中,它們的漸近分布都只和自相關(guān)系數(shù)真值有關(guān)。特別值得注意的是,定理6 的實(shí)際意義在于它可用于對模型單個(gè)變點(diǎn)的假設(shè)H0:ρ2-ρ1=λ0進(jìn)行檢驗(yàn),其中λ0不一定為0。當(dāng)λ0= 0 時(shí),假設(shè)H0:ρ2-ρ1=λ0的檢驗(yàn)等價(jià)于假設(shè)H0:ρ2=ρ1的檢驗(yàn),即檢驗(yàn)是否存在變點(diǎn)。下面討論更一般的簡單假設(shè)檢驗(yàn)H0:ρ2-ρ1=λ0。 本小節(jié)主要通過模擬數(shù)據(jù)對第1 節(jié)中所提的方法及相關(guān)結(jié)論進(jìn)行檢驗(yàn)。假定數(shù)據(jù)生成模型為 下面模擬不同參數(shù)取值下模型自相關(guān)系數(shù)極大似然(或擬似然)估計(jì)?ρ1、?ρ2在q=o(p),p →∞時(shí)的收斂情況。模擬實(shí)驗(yàn)重復(fù)進(jìn)行10 000 次,其中q= 80,25,6 對應(yīng)的p=20,275,994,此時(shí)q/p逐步增大。記錄自相關(guān)系數(shù)極大似然(或擬似然)估計(jì)值的均方誤差,得到結(jié)果見表1。 表1 隨機(jī)模擬結(jié)果 從表1 可以看出,隨著p的增大,自相關(guān)系數(shù)極大似然(或擬似然)估計(jì)?ρ1、?ρ2的均方誤差都有趨于零的特征,表明自相關(guān)系數(shù)極大似然(或擬似然)估計(jì)值收斂到真值,自相關(guān)系數(shù)極大似然(或擬似然)估計(jì)分別是對應(yīng)參數(shù)真值的一致估計(jì)。 下面將帶有變點(diǎn)的模型(1)應(yīng)用于實(shí)證研究,主要分析上證綜合指數(shù)日成交量從1998 年1 月5 日至2003 年1 月29 日的1 221 個(gè)數(shù)據(jù)的變點(diǎn)檢驗(yàn)問題,其時(shí)間序列圖見圖1。 圖1 上證綜合指數(shù)日成交量時(shí)序圖 對于上證綜合指數(shù)日成交量序列的樣本自相關(guān)和偏自相關(guān)系數(shù),如圖2 和圖3 所示,其中樣本的自相關(guān)系數(shù)呈指數(shù)遞減趨勢,表現(xiàn)為拖尾性;偏自相關(guān)系數(shù)表現(xiàn)為1 階截尾性質(zhì),初步選擇AR(1)模型刻畫該序列。 圖2 上證綜合指數(shù)日成交量序列的自相關(guān)系數(shù) 圖3 上證綜合指數(shù)日成交量序列的偏自相關(guān)系數(shù) 對該時(shí)間序列,需要找出其變點(diǎn)位置。通過對不同q值做假設(shè)檢驗(yàn)H0:ρ2-ρ1=0 得到變點(diǎn)位置,與劉琴[21]通過極大似然比方法得到的變點(diǎn)位置一致。本文基于此變點(diǎn)位置主要研究H0:ρ2-ρ1=λ0的檢驗(yàn)問題。由于模型參數(shù)的極大似然(或擬似然)估計(jì)值如表2 所示,則可構(gòu)建假設(shè)H0:ρ2-ρ1=-0.270 4 進(jìn)行檢驗(yàn),以確定該序列在此位置存在變點(diǎn)且自相關(guān)系數(shù)增量為-0.270 4。在原假設(shè)成立條件下,由定理6,有,從而可得到?λ在1-α=0.95 的顯著性水平下的臨界點(diǎn)u1=-0.318 3,u2=-0.222 5,故在95%的顯著性水平下可考慮接受原假設(shè),即可以認(rèn)為該序列在t=80 時(shí)刻存在持久性變點(diǎn)且ρ20=ρ10-0.270 4。該實(shí)證研究表明本文所提出的方法是方便且有效的。 表2 極大似然(或擬似然)的估計(jì)結(jié)果 本文主要研究了帶單個(gè)變點(diǎn)AR(1)模型的統(tǒng)計(jì)推斷問題。基于極大似然(或擬似然)方法,本文給出了模型參數(shù)極大似然(或擬似然)估計(jì)的一種表達(dá)形式,得到了一般條件下自相關(guān)系數(shù)極大似然(或擬似然)估計(jì)一致收斂到參數(shù)真值的特征,并給出了其漸近分布,同時(shí)通過該分布,解決了對變點(diǎn)是否存在的簡單假設(shè)的檢驗(yàn)問題。數(shù)值模擬驗(yàn)證了自相關(guān)系數(shù)極大似然(或擬似然)估計(jì)一致性;實(shí)證分析的結(jié)果表明了變點(diǎn)存在問題的檢驗(yàn)方法的有效性,該檢驗(yàn)方法具有一定的實(shí)際意義。
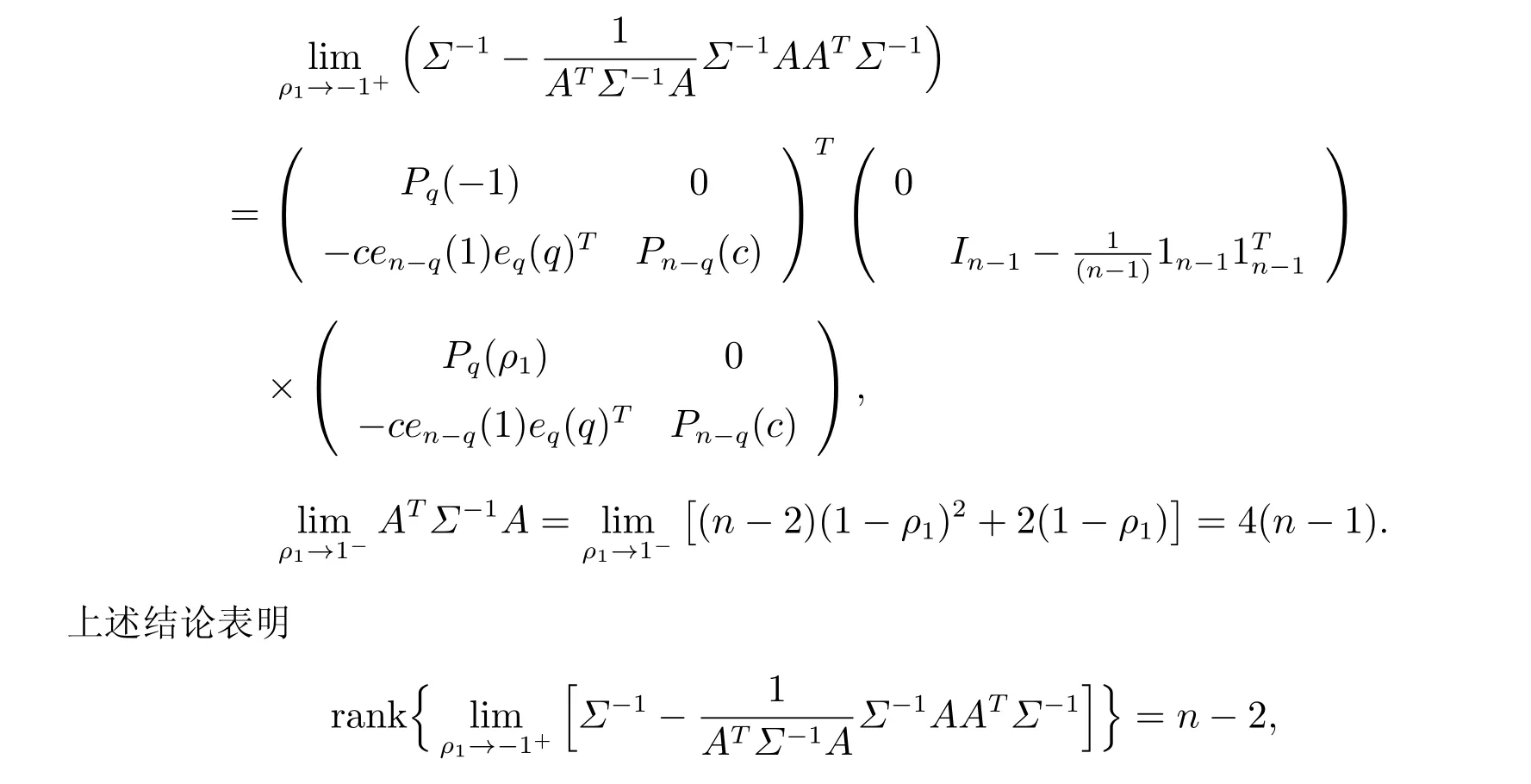



1.2 自相關(guān)系數(shù)估計(jì)的一致性
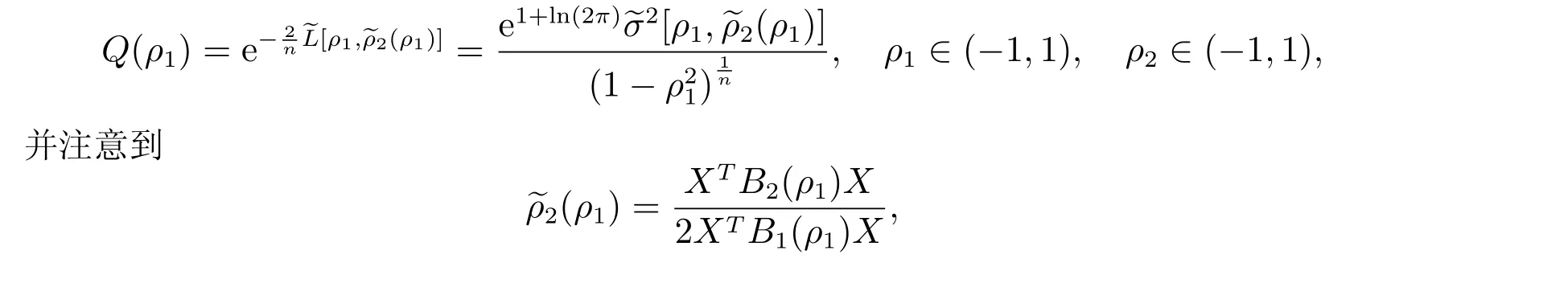

1.3 估計(jì)的漸近分布



2 模擬研究和實(shí)證分析
2.1 自相關(guān)系數(shù)估計(jì)一致性的數(shù)值模擬

2.2 實(shí)證分析



3 總結(jié)

