半二面體群上的三度連通邊傳遞雙凱萊圖分類(lèi)

曹建基, 王俊新,, 張咪咪

(1.山西財(cái)經(jīng)大學(xué)應(yīng)用數(shù)學(xué)學(xué)院，太原 030006; 2.河北師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，石家莊 050024)

0 引言

圖的對(duì)稱(chēng)性研究是代數(shù)圖論領(lǐng)域的重要研究課題之一，在編碼、密碼、計(jì)算機(jī)網(wǎng)絡(luò)設(shè)計(jì)等領(lǐng)域有著廣泛的應(yīng)用。本文將討論一類(lèi)三度邊傳遞雙凱萊圖，考慮其分類(lèi)。

本文所考慮的群都為有限群，所有的圖都為有限、連通、簡(jiǎn)單無(wú)向圖。設(shè)Γ=(V,E)為一個(gè)圖，其中頂點(diǎn)集為V，邊集為E。Aut(Γ)表示圖Γ的全自同構(gòu)群。若Aut(Γ)作用在集合V(Γ)、E(Γ)和A(Γ)上傳遞，那么分別稱(chēng)圖Γ為點(diǎn)傳遞圖、邊傳遞圖和弧傳遞圖。設(shè)G為集合?上的置換群，且設(shè)α ∈?。記Gα為α在G中的點(diǎn)穩(wěn)定化子，即群G中保持α不變的元素生成的子群。稱(chēng)G在集合?上作用半正則，如果對(duì)任意的α ∈?，都有Gα= 1。如果G在集合?上作用傳遞且半正則，那么稱(chēng)G作用正則。眾所周知，Γ為凱萊圖當(dāng)且僅當(dāng)它存在一個(gè)自同構(gòu)群作用在Γ的點(diǎn)集上正則[1]。如果圖Γ有一個(gè)半正則自同構(gòu)群H，其作用在圖Γ的點(diǎn)集上有兩個(gè)相同長(zhǎng)度的軌道，那么稱(chēng)Γ為群H上的雙凱萊圖。凱萊圖通常如下定義：給定一個(gè)群G和一個(gè)非空子集S，滿(mǎn)足S ?G{1}且S-1=S。定義群G上的關(guān)于S的凱萊圖為Cay(G,S)，頂點(diǎn)集為G，邊集為{{g,s}|g ∈G,s ∈S}。類(lèi)似地，雙凱萊圖如下定義：設(shè)H為群。R、L和S為H的子集，滿(mǎn)足R-1=R,L-1=L且R ∪L不包含H的單位元。H上的關(guān)于三元集合(R,L,S)的雙凱萊圖記作BiCay(H,R,L,S)，頂點(diǎn)集為H0∪H1，其中H0={h0|h ∈H},H1={h1|h ∈H}，邊集為{{h0,g0}|gh-1∈R},{{h1,g1}|gh-1∈L}和{{h0,g1}|gh-1∈S}三者的并集。設(shè)Γ=BiCay(H,R,L,S)，對(duì)g ∈H，定義Γ的點(diǎn)集上的一個(gè)置換R(g)：

則R(H)={R(g)|g ∈H}為Aut(Γ)的一個(gè)同構(gòu)于H的半正則子群，作用在Γ的點(diǎn)集上有兩個(gè)軌道H0和H1。若R(H)為Aut(Γ)的正規(guī)子群，則雙凱萊圖Γ= BiCay(H,R,L,S)為H上的正規(guī)雙凱萊圖[2]。另外，若|R| =|L| =s，則BiCay(H,R,L,S)被稱(chēng)為s-型雙凱萊圖。特別地，當(dāng)|S| = 1 時(shí)，雙凱萊圖Γ= BiCay(H,R,L,S)也被稱(chēng)作H上的1-匹配雙凱萊圖。群論和圖論中未提及的符號(hào)和術(shù)語(yǔ)，參見(jiàn)文獻(xiàn)[3–4]。

在雙凱萊圖的研究中，相當(dāng)多的研究者關(guān)注下面的一個(gè)很自然的問(wèn)題：對(duì)給定的群H，分類(lèi)H上具有特殊對(duì)稱(chēng)性的雙凱萊圖。例如，循環(huán)群上的三度點(diǎn)傳遞(邊傳遞)雙凱萊圖，在文獻(xiàn)[5–6]中給出了完全分類(lèi)。循環(huán)群上的所有四度邊傳遞雙凱萊圖也在文獻(xiàn)[7]中給出了刻畫(huà)，在文獻(xiàn)[8]中給出了內(nèi)交換p-群上的三度邊傳遞雙凱萊圖的分類(lèi)。交換群上的三度點(diǎn)傳遞雙凱萊圖的完全分類(lèi)也在文獻(xiàn)[9]中被給出。

受上面結(jié)論的啟發(fā)，在本文中，我們將研究半二面體群上的三度邊傳遞雙凱萊圖。對(duì)任意偶數(shù)n ≥2，4n階半二面體群如下定義

注意到交換群上的三度雙凱萊圖已經(jīng)在文獻(xiàn)[9]中給出了完全分類(lèi)，下面設(shè)n ≥4。本文中，我們將給出半二面體群上的三度連通邊傳遞雙凱萊圖的完全分類(lèi)。

1 預(yù)備知識(shí)

1.1 雙凱萊圖的基本性質(zhì)

在這一部分中，我們?cè)O(shè)Γ=BiCay(H,R,L,S)為群H上的雙凱萊圖。下面將給出Γ的一些基本性質(zhì)。

引理1[2]設(shè)Γ=BiCay(H,R,L,S)為群H上的雙凱萊圖，則下面結(jié)論成立：

1)H可由R ∪L ∪S生成；

2) 在圖同構(gòu)的意義下，S可以包含H的單位元1；

3) 對(duì)H的任意自同構(gòu)α，都有BiCay(H,R,L,S)?BiCay(H,Rα,Lα,Sα)；

4) BiCay(H,R,L,S)?BiCay(H,L,R,S-1)。

若群H的三個(gè)子集R、L、S滿(mǎn)足R=R-1,L=L-1且1∈S，則稱(chēng)三元有序組(R,L,S)為群H上的雙凱萊圖三元組。設(shè)(R,L,S)和(R′,L′,S′)為兩個(gè)群H上的雙凱萊三元組。如果存在H的自同構(gòu)α滿(mǎn)足(R′,L′,S′) = (R,L,S)α或(R′,L′,S′) =(L,R,S-1)α，那么稱(chēng)(R,L,S)和(R′,L′,S′)等價(jià)，記為(R,L,S)≡(R′,L′,S′)。由引理1 中的3)和4)，可得同一群H上的兩個(gè)等價(jià)的雙凱萊三元組決定的雙凱萊圖定同構(gòu)。

下面給出幾個(gè)和雙凱萊圖的自同構(gòu)相關(guān)的結(jié)果。設(shè)α是H的一個(gè)自同構(gòu)，x,y,g ∈H，定義V(Γ)=H0∪H1的兩個(gè)置換

令

引理2[2]設(shè)Γ= BiCay(H,R,L,S)是H上的一個(gè)連通雙凱萊圖，那么當(dāng)I=?時(shí)，NAut(Γ)(R(H))=R(H)?F；當(dāng)I ?=?時(shí)，NAut(Γ)(R(H))=R(H)〈F,δα,x,y〉，其中δα,x,y ∈I。進(jìn)一步，對(duì)任意δα,x,y ∈I，下面結(jié)果成立：

1)〈R(H),δα,x,y〉在V(Γ)上作用傳遞；

2) 如果α是二階元且x=y= 1，那么Γ同構(gòu)于Cay(ˉH,R ∪αS)，其中ˉH=H?〈α〉。

引理3[9]設(shè)Γ= BiCay(H,R,L,{1})為群H上的1-匹配雙凱萊圖，則Aut(Γ)中存在包含R(H)的正則子群的充要條件是存在H的階至多是2 的自同構(gòu)α，滿(mǎn)足Rα=L。

引理4[10]設(shè)Γ=BiCay(H,R,L,S)為群H上的雙凱萊圖，如果R ∩L ?=?或S包含二階元，那么Γ的圍長(zhǎng)至多是4。

引理5[10]設(shè)Γ=BiCay(H,R,L,S)為群H上的雙凱萊圖，如果Γ為邊傳遞但不點(diǎn)傳遞，那么Γ為0-型圖。

1.2 三維立方體Q3 的循環(huán)覆蓋

下面我們介紹圖CQ(t,m)。設(shè)Q3= F008A 為立方體，如圖1 所示。設(shè)T為Q3的由邊集{ax,ay,az,bw,bz,cz,dy}得到的生成樹(shù)。

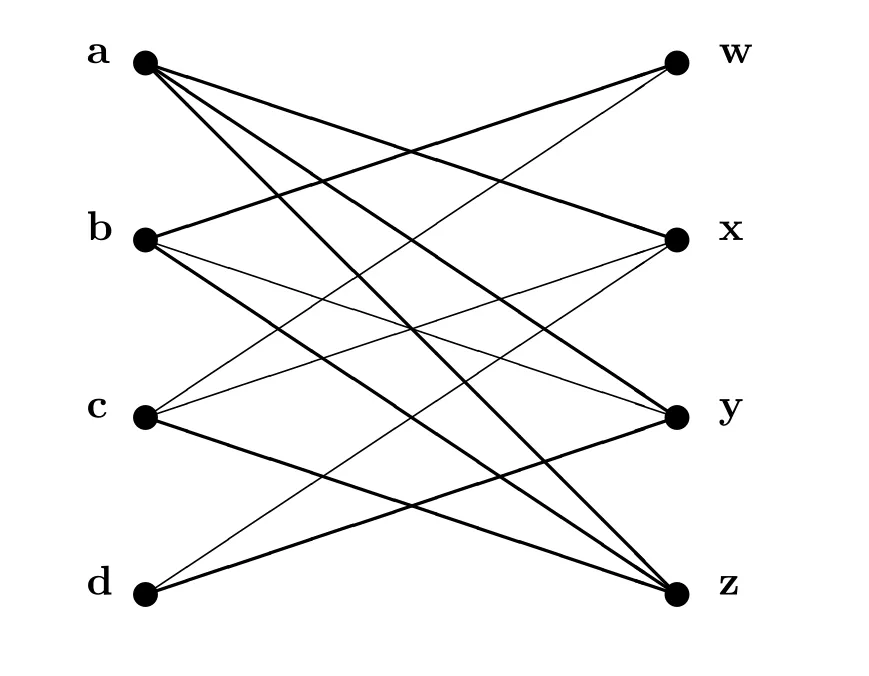
圖1 立方體圖

設(shè)m、t為兩個(gè)整數(shù)，滿(mǎn)足1≤t ≤m-1 且(t,m)=1，可得t ∈Z?m。記t-1為t在Z?m中的逆元，則圖CQ(t,m)有點(diǎn)集V(CQ(t,m))=V(Q3)×Zm和邊集

圖Γ的s-弧是指Γ的s+1 個(gè)頂點(diǎn)構(gòu)成的有序序列(v0,v1,···,vs-1,vs)，滿(mǎn)足{vi-1,vi}∈E(Γ)，其中1≤i ≤s，且vi-1?=vi+1對(duì)1≤i ≤s-1 都成立。特別地，1-弧通常叫作弧。設(shè)G為Aut(Γ)的子群，如果對(duì)Γ的任意兩個(gè)s-弧，存在唯一的元素g ∈G，把一個(gè)s-弧映射到另一個(gè)s-弧，那么群G稱(chēng)為s-弧正則。如果Aut(Γ)為s-弧正則，圖Γ被稱(chēng)作s-弧正則。

下面引理給出了立方體Q3的循環(huán)覆蓋。

1.3 半二面體群的性質(zhì)

下面給出半二面體群的一些簡(jiǎn)單性質(zhì)。

引理7 設(shè)SD4n為4n階半二面體群，則下面結(jié)論成立：

1)SD4n=〈a〉∪b〈a〉，其中b〈a〉={ba2i}∪{ba2i+1}, 0≤i ≤n-1。進(jìn)一步有，集合{ba2i}中每個(gè)元素階均為2，集合{ba2i+1}的每個(gè)元素階均為4；

2) Aut(SD4n)作用在集合{ba2i}和{ba2i+1}均傳遞，其中0≤i ≤n-1；

3) 如果SD4n=〈x,y〉，那么存在α ∈Aut(SD4n)，把集合{x,y}映射到集合{a,b}、{ba,b}、{ba,a}之一。

證明 由半二面體群的定義容易得到SD4n=〈a〉∪b〈a〉。取bak ∈b〈a〉，其中i ∈Z2n，則有

因?yàn)閍的階為2n，所以結(jié)論1)成立。

對(duì)于結(jié)論2)，由直接計(jì)算可得

所以存在α ∈Aut(SD4n)，滿(mǎn)足α把集合{a,ba2i}映射到集合{a,b}。

類(lèi)似地，由直接計(jì)算可得

存在β ∈Aut(SD4n)，滿(mǎn)足β把集合{a,ba2i+1}映射到集合{a,ba}，所以結(jié)論2)成立。

對(duì)于結(jié)論3)，令SD4n=〈x,y〉，由半二面體群的結(jié)構(gòu)得x和y至少有一個(gè)元素不在〈a〉中。不失一般性，我們?cè)O(shè)y/∈〈a〉，如果y的階為2，那么由結(jié)論2)可得，存在α1∈Aut(SD4n)，滿(mǎn)足yα1=b。因?yàn)椤磝α1,b〉 =SD4n，所以xα1=ai或bai，其中i與2n互素。ai、b能生成SD4n，且ai、b和a、b滿(mǎn)足相同的定義關(guān)系，故一定存在α2∈Aut(SD4n)，滿(mǎn)足(ai)α2=a且bα2=b。因此，{x,y}α1α2={a,b}或者{ba,b}。

如果y的階為4，那么由結(jié)論2)得，存在β1∈Aut(SD4n)，滿(mǎn)足yβ1=ba。因?yàn)椤磝β1,ba〉=SD4n，所以可得xβ1=ai或baai，其中i與2n互素。ai、ba可以生成SD4n，且ai、ba和a、ba滿(mǎn)足相同的定義關(guān)系，故一定存在β2∈Aut(SD4n)，使得(ai)β2=a且(ba)β2=ba，故{x,y}β1β2={a,ba}或{ba2,ba}。容易驗(yàn)證映射c:ba2能誘導(dǎo)出一個(gè)SD4n的自同構(gòu)滿(mǎn)足{b,ba}c={ba2,ba}，故結(jié)論3)成立。

1.4 三度邊傳遞圖的性質(zhì)

設(shè)Γ為圖，且設(shè)G ≤Aut(Γ)。如果G作用在圖Γ的弧集(邊集)上傳遞，那么Γ被稱(chēng)作G-弧傳遞(G-邊傳遞)。設(shè)Γ為一個(gè)G-邊傳遞圖，且設(shè)N為群G的正規(guī)子群。

圖Γ的關(guān)于子群N的商圖ΓN如下定義。點(diǎn)集為N作用在點(diǎn)集V(Γ)上軌道的集合，若存在一條圖Γ的邊，滿(mǎn)足兩個(gè)頂點(diǎn)分別屬于兩個(gè)不同的軌道，則稱(chēng)這兩個(gè)軌道相鄰(連邊)。如果Γ和ΓN度數(shù)相同，那么圖Γ恰好是ΓN的一個(gè)N-覆蓋。下面介紹一個(gè)引理。

引理8[12]設(shè)Γ為三度G-弧傳遞圖，如果NG作用在V(Γ)上至少有兩個(gè)軌道，那么N作用在V(Γ)上半正則。ΓN為三度弧傳遞圖且G/N是ΓN的一個(gè)弧傳遞子群，Γ是ΓN的正則N-覆蓋。

2 主要結(jié)論

在此節(jié)中，設(shè)Γ= BiCay(H,R,L,S)為群H ?SD4n上的三度連通雙凱萊圖，其中n ≥4。

引理9 如果Γ為0-型圖，那么Γ為凱萊圖。

證明 因?yàn)棣?-型，我們可得R=L=?。由引理1 的結(jié)論1)和結(jié)論2)，可設(shè)S={1,x,y}且SD4n=〈x,y〉。由引理7 的結(jié)論3)，可得S為子集{1,a,b}、{1,ba,b}、{1,a,ba}之一。

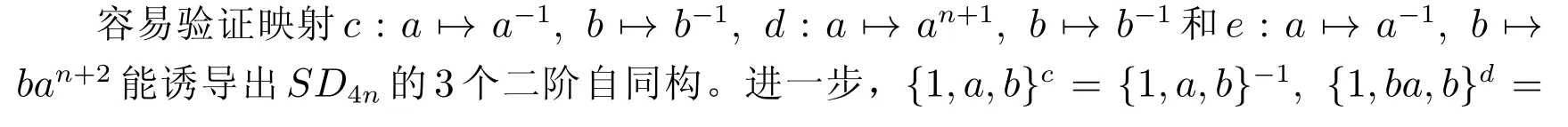
結(jié)論得證。

若一個(gè)圖的自同構(gòu)群包含一個(gè)循環(huán)半正則子群作用在圖的頂點(diǎn)集上有四個(gè)軌道，則此圖被稱(chēng)為四循環(huán)圖。所有的三度弧傳遞四循環(huán)圖在文獻(xiàn)[13]中給出了分類(lèi)，結(jié)論如下。

引理10[13]三度四循環(huán)圖弧傳遞，當(dāng)且僅當(dāng)它同構(gòu)于下面圖之一：

1) F008A、F020A、F020B、F024A、F028A、F032A、F040A；2) F016A、F048A、F056C、F060A、F080A、F096A、F112B、F120B、F224C、F240C；

3) CQ(t,m)，其中2≤t ≤m-3 且m|(t2+t+1)；

4) CQ(2t-1,2m)，其中2≤t ≤m-1 且m|(4t2-2t+1)。

引理11 設(shè)R={b},L={ba2t},S={1,a}，其中t為奇數(shù)，3≤t ≤n-3 且n| 2(t2+t+1)，則Γ為立方體F008A 的1-弧正則Zn-覆蓋。

顯然，K可以由a-1cb、c和ca生成。下面證明a-1cb、c、ca和元素a、b、c滿(mǎn)足相同的定義關(guān)系。首先，c和ca都為二階元，直接計(jì)算可得

注意到

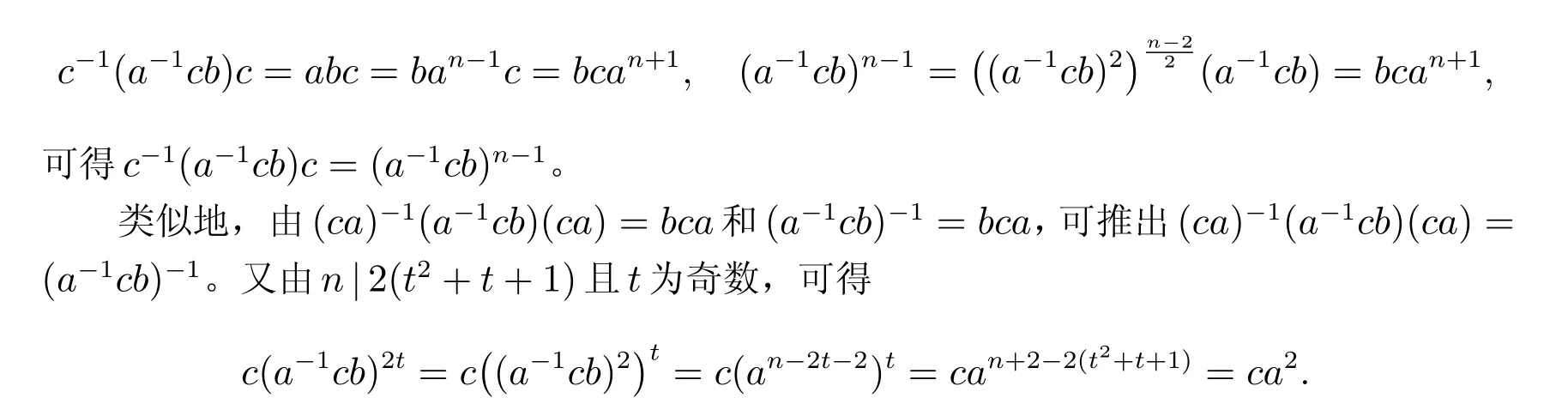
另一方面，(ca)-1c(ca)=a-1ca=c-1a2=ca2，因此(ca)-1c(ca)=c(a-1cb)2t。

因?yàn)閍-1cb、c、ca與元素a、b、c有相同的定義關(guān)系，所以由映射-1cb,,可誘導(dǎo)K的一個(gè)自同構(gòu)β，并且滿(mǎn)足bβ=c,cβ=ca, (ca)β=(ca)a-1cb=b，即β為集合{b,c,ca}中元素的循環(huán)置換，故β ∈Aut(K,{b,c,ca})，Σ為弧傳遞。注意到(a2)β=(a-1cb)2=an-2t-2∈〈a2〉，β正規(guī)化N=〈R(a2)〉。顯然，N ?Zn在R(K)中正規(guī)。因此，NR(K)?Aut(K,{b,c,ca})。由引理8 可得商圖ΣN同構(gòu)于立方體F008A，且Σ為F008A 的一個(gè)N-覆蓋。注意到N ?Zn，Σ同構(gòu)于引理6 中結(jié)論1)和結(jié)論2)中的一個(gè)圖，容易得到n= 14,t= 9 或t= 11，滿(mǎn)足n|2(t2+t+1)且3≤t ≤n-3。另外，n= 14 為滿(mǎn)足條件n|2(t2+t+1)且3≤t ≤n-3 的最小值，故Γ至少有112 個(gè)頂點(diǎn)。進(jìn)一步，可得Σ同構(gòu)于引理6 結(jié)論1)中的一個(gè)圖，故Σ為1-弧正則，引理得證。

引理12 設(shè)Γ= BiCay(H,R,L,S)為立方體的N-覆蓋，且N ?Zn對(duì)某個(gè)n>1，且設(shè)圖Γ的保簇自同構(gòu)群作用在Γ上弧傳遞。如果Γ為1-弧正則，那么NA=Aut(Γ),A/N ?A4×Z2且N ≤R(H)。進(jìn)一步有，A中存在包含R(H)的正規(guī)正則子群G。

證明 如果Γ為1-弧正則，那么A恰好為Γ的保簇自同構(gòu)群。由文獻(xiàn)[11]，可得A/N?A4×Z2。設(shè)G/N為A/N的Sylow 2-子群，因?yàn)锳/N ?A4×Z2，故G/N ?Z2×Z2×Z2，且G/N為A/N的正規(guī)正則子群。因此，G也在V(Γ)上正則。若R(H)N/N不是2-群，則由R(H)∩N為R(H)的循環(huán)正規(guī)子群，得R(H)∩N ≤〈R(a)〉，故

注意到|〈ai〉|被3 整除，可得R(H)/(R(H)∩N)定包含子群同構(gòu)于Z3?Z2。另一方面，A/N?((Z2×Z2)?Z3)×Z2中沒(méi)有子群同構(gòu)于Z3?Z2，矛盾。因此，R(H)/N為2-群。進(jìn)一步，R(H)/N ≤G/N隱含著R(H)≤G。因?yàn)镽(H)?SD4n，R(H)的每個(gè)Sylow 2-子群同構(gòu)于〈ai〉?〈b〉，其中〈ai〉為〈a〉的Sylow 2-子群，故R(H)/N ?Z2×Z2。因此，|R(H):R(H)∩N|=4 且|R(H)∩N|=|N|=n。最后，可得N ≤R(H)。

定理1Γ為三度連通邊傳遞圖當(dāng)且僅當(dāng)雙凱萊圖的三元有序組(R,L,S)等價(jià)于下面情形之一。進(jìn)一步，可得所有的圖均為弧傳遞。

1)n=4, (R,L,S)≡({b},{ba4},{1,a})且Γ同構(gòu)于F032A。

2)n=6, (R,L,S)≡({b},{ba2},{1,a})且Γ同構(gòu)于F048A。

3) (R,L,S)≡({b},{ba2t},{1,a})，其中t為奇數(shù)，3≤t ≤n-3 且n|2(t2+t+1)，Γ同構(gòu)于CQ(t,n)。

4)n=4, (R,L,S)≡({b,ba2},{a,a-1},{1})且Γ同構(gòu)于F032A。

5)n=10, (R,L,S)≡({b,ba6},{a,a-1},{1})且Γ同構(gòu)于F080A。

6)n=12, (R,L,S)≡({b,ba2},{a,a-1},{1})且Γ同構(gòu)于F096A。

證明 由引理11 可得到定理1 的情形3)中圖的弧傳遞性。由文獻(xiàn)[14]，我們可以證明定理1 的情形1)～6)中其余圖的弧傳遞性。

為完成定理證明，只需要證明必要性。容易得到〈R(a)〉為循環(huán)半正則子群，且作用在V(Γ)上有四個(gè)軌道，故Γ為一個(gè)四循環(huán)圖。由引理5 和引理9，Γ為弧傳遞，故Γ為引理10 中的一個(gè)圖。

因?yàn)閚 ≥4，Γ至少有32 個(gè)頂點(diǎn)。由文獻(xiàn)[15]中主要結(jié)論得引理10 中1)和2)中的圖除去F008A 外，圍長(zhǎng)均大于4。如果Γ為引理10 中3)和4)中的圖，那么Γ為立方體的1-弧正則覆蓋。由文獻(xiàn)[11]中主要結(jié)論，可得Γ圍長(zhǎng)至少為6，故Γ圍長(zhǎng)大于4。

若Γ為0-型圖，則R=L=?。由Γ的連通性得H=〈S〉。因?yàn)镠 ?SD4n，由引理7 的結(jié)論3)，可得S為子集{1,a,b}、{1,ba,b}、{1,a,ba}之一。如果S ?={1,a,ba}，那么S包含二階元。由引理4，Γ圍長(zhǎng)為4，矛盾。設(shè)S={1,a,ba}，則Γ中可找到4-圈(10,a1,(ban+2)0,(ba)1)，矛盾。

我們僅需考慮下面兩種情形。

情形1Γ為1-型圖。

設(shè)R={u},L={v}且S={1,w}。因?yàn)镽=R-1,L=L-1，所以u(píng)和v均為二階元。Γ圍長(zhǎng)至少為5，由引理4 得u ?=v且w不是二階元。令H=〈u,v,w〉，由引理7 中結(jié)論2)得，可設(shè)u=b,v=an或baj,w=ai或bai，其中j為偶數(shù)，i為奇數(shù)。如果Γ同構(gòu)于引理10 中1)和2)中的圖，那么n ≤30。由文獻(xiàn)[14]得n= 4 且(R,L,S)≡({b},{ba4},{1,a})或者n=6 且(R,L,S)≡({b},{ba2},{1,a})，故Γ同構(gòu)于定理1 的情形1)和情形2)中的圖之一。

如果Γ同構(gòu)于引理10 中3)和4)中的圖，那么Γ為立方體Q3上的1-弧正則N-覆蓋，其中N ?Zn對(duì)某個(gè)整數(shù)n。令A(yù)= Aut(Γ)，由引理12，A/N ?A4×Z2。進(jìn)一步，A中存在包含R(H)的正規(guī)正則子群G，故存在g ∈G，滿(mǎn)足1g0= 11。因?yàn)镽(H)G，由引理2，g=δα,x,y對(duì)某個(gè)α ∈Aut(H)且x,y ∈H，則

故x= 1。由δα,x,y的定義可得Rα=L,Lα=y-1Ry且Sα=y-1S-1，故uα=v,v=baj對(duì)某個(gè)偶數(shù)j ∈Zn。因此，(R,L,S)≡({b},{baj},{1,ai})或者(R,L,S)≡({b},{baj},{1,bai})。下面，再分兩種子情況討論。

情形1.1S={1,ai}。

由引理12 可知N ≤R(H)。設(shè)c為群H的由映射誘導(dǎo)的自同構(gòu)，易得c為二階元且滿(mǎn)足Rc=L,Lc=R且Sc=S-1。進(jìn)而，可得δc,1,1為Γ的二階自同構(gòu)且K=〈R(H),δc,1,1〉作用在V(Γ)上傳遞。由N ≤R(H)，得K/N ?Z32。又因?yàn)锳/N?A4×Z2，我們有K/NA/N，即KA，故Γ能看作群K上的正規(guī)凱萊圖。令

故a2t2=a(n-2-2t)且2t2≡n-2-2t(mod 2n)，所以n|2(t2+t+1)。注意到|Γ| =8n且n為偶數(shù)，我們可得Γ同構(gòu)于引理10 中4)型圖。所以Γ ～= CQ(t,n)，其中t為奇數(shù)，且3≤t ≤n-3，故Γ同構(gòu)于定理1 中情形3)型圖。

情形1.2S={1,bai}。

設(shè)Γ ?BiCay(H,{b},{baj},{1,bai})。下面我們?cè)俜謨煞N子情形考慮。

情形1.2.1 (i,2n)?=1。

由(i,2n)?=1，可得i為奇數(shù)且(i,n)?=1。另外，由Γ的連通性，可得〈a〉=〈ai,aj〉。進(jìn)一步，可得(i,j)=1，故j ?=n。我們考慮Γ的距離點(diǎn)11為4 的子圖，可得

情形1.2.2 (i,2n)=1。

在此情形下，由映射d:ai a,可誘導(dǎo)出Γ的自同構(gòu)。Γd ?BiCay(H,{b},{bak},{1,ba})，其中k為偶數(shù)。我們考慮Γ的距離點(diǎn)10為4 的子圖，可得

分析Γ4(10)內(nèi)的點(diǎn)的重合情況，我們得到，如果k ?≡2,n,n+2(mod 2n)，那么過(guò)邊{10,11}和{10,(ba)1}有唯一的8-圈(10,11,(ban+1)0,(ban+1)1,(an)0,(an)1,(ba)0,(ba)1)。另一方面，不存在過(guò)邊{10,b0}的8-圈，與圖Γ的邊傳遞性矛盾。下面只需要考慮k ≡2,n,n+2(mod 2n)的情形。

如果k ≡2(mod 2n)，那么Γ ?BiCay(H,{b},{ba2},{1,ba})。考慮Γ的距離點(diǎn)10為4 的子圖，我們可得過(guò)邊{10,11}和{10,(ba)1}有3 個(gè)8-圈(10,11,(ban+1)0,(ban+1)1,(an)0,(an)1, (ba)0,(ba)1), (10, 11, (ban+1)0, (ban+1)1, (an)0, (ban)0, (a-1)1, (ba)1)以及(10, 11,(ban+1)0,(an+1)0,(ban+2)1,(an)1,(ba)0,(ba)1)。另一方面，不存在過(guò)邊{10,b0}的8-圈，這與圖Γ的邊傳遞性矛盾。

如果k ≡n(mod 2n)，那么Γ ?BiCay(H,{b},{ban},{1,ba})。類(lèi)似地，考慮Γ的距離點(diǎn)10為4 的子圖，可得過(guò)邊{10,11}和{10,b0}有3 個(gè)8-圈(10,11,(ban+1)0,(ban+1)1,(an)0, (an)1,b1,b0), (10, 11, (ban)1, (ban)0, (an)0, (an)1,b1,b0)和(10, 11, (ban)1, (ban)0,(a-1)1,(a-1)0,b1,b0)。另一方面，不存在過(guò)邊{10,(ba)1}的8-圈，與圖Γ的邊傳遞性矛盾。

如果k ≡n+2(mod 2n)，那么Γ ?BiCay(H,{b},{ban+2},{1,ba})。容易得到Γ的部分圖中存在4-圈(10,(ba)1,(an-1)1,b0)，這與Γ的圍長(zhǎng)大于4 矛盾。

情形2Γ為2-型。

設(shè)R={u,v},L={x,y},S={1}，其中u,v,x,y ∈H。注意到，Γ圈長(zhǎng)大于4。由引理4，R ∩L=?。若u、v均為二階元，則uv ?=vu。類(lèi)似地，若x、y均為二階元，則xy ?=yx。

由引理7，設(shè)R={b,ba2i},L={al,a-l}，其中1≤i,l ≤n- 1。先設(shè)Γ為引理10 的1)和2)中的圖之一，則n ≤30。由文獻(xiàn)[14]可知，n= 4 且(R,L,S)≡({b,ba2},{a,a-1},{1})，或者n= 10 且(R,L,S)≡({b,ba6},{a,a-1},{1})，或者n=12 且(R,L,S)≡({b,ba2},{a,a-1},{1})，故Γ同構(gòu)于定理1 中情形4)～6)型圖。由引理10，設(shè)Γ為立方體F008A 上的1-弧正則N-覆蓋，其中N ?Zn對(duì)某個(gè)整數(shù)n。令A(yù)= Aut(Γ)，由引理12 可得A/N ?A4×Z2。進(jìn)一步，得N ≤R(H)且A中存在正規(guī)正則子群G滿(mǎn)足R(H)≤G。因?yàn)棣?-型圖，由引理3，群H有一個(gè)階至多是2 的自同構(gòu)c滿(mǎn)足Rc=L，故R和L由二階元組成。注意到〈R,L〉?=H，與群H的結(jié)構(gòu)矛盾。

綜合以上幾種情形，定理得證。