談初中數學建模的基本類型和應用

林沁瑤

數學建模是指根據實際建立數學模型，對數學模型進行分析和求解，以解決實際問題。數學建模是全面提升數學核心素養、推進中學數學素質教育的重要組成部分。提高學生的數學建模能力是落實數學核心素養的根本途徑和要求。教師應從引導學生建立數學模型解決實際問題出發，培養學生數學建模思想，讓學生深入認識數學學科的特點，真正意識到數學來源于生活又應用于生活。

一、建立二次函數模型解決實際問題

新課標要求會用適當的函數表示和刻畫一些實際問題中變量與變量之間的關系，初步預測變量的變化規律，從而用函數來解決簡單的實際問題。學生在初中階段學習了一次函數、反比例函數和二次函數后，意識中有了這些基本函數的模型。因此，面對一些實際問題就可以引導學生嘗試通過建立函數模型來解決。

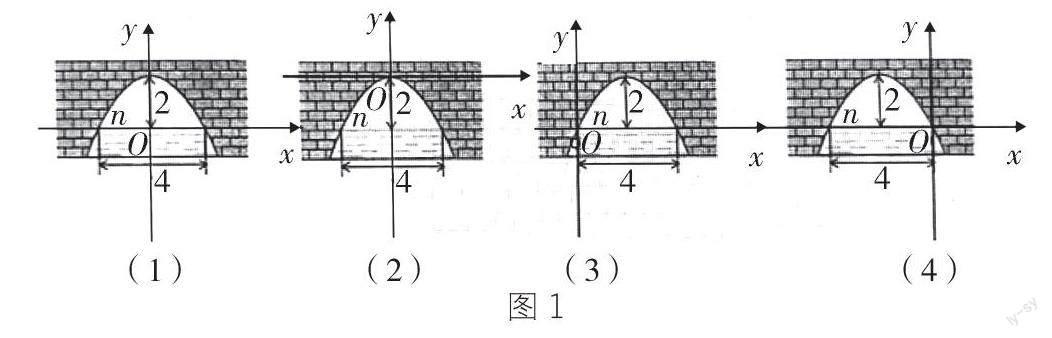
例：潮州西湖里有一條形如拋物線的小拱橋，如圖1，當湖面在如圖所示的n位置時，拱橋頂（弧的中點）離湖面為2 m ，湖面寬 4 m；當湖面比原來下降 1 m時，問此時水面寬度為多少？水面寬度增加多少 ？

本題是考查以函數為背景的函數型數學模型的問題，學生要解決此問題，首先就要建立函數模型把實際問題轉化為函數問題。難點在于如何分析判斷這是學過的哪種基本函數模型。從題目中的“拋物線”不難聯想到二次函數圖像的形狀，因此，可以利用二次函數相關的知識解決此問題。由于圖像是建立在坐標系中研究的，所以建立適當的平面直角坐標系是解答本題的關鍵（圖1展示了四種不同的建立坐標系模型），再根據函數圖像的特征設函數的解析式，并求出相應的二次函數的解析式，進而解決問題。

二、建立幾何模型解決實際問題

初中幾何圖形的學習有很多是三角形、四邊形和圓等幾何圖形的推理證明。幾何中的數學建模就是根據幾何的基本圖形構造模型，需要較強的圖形構造能力和空間想象能力。

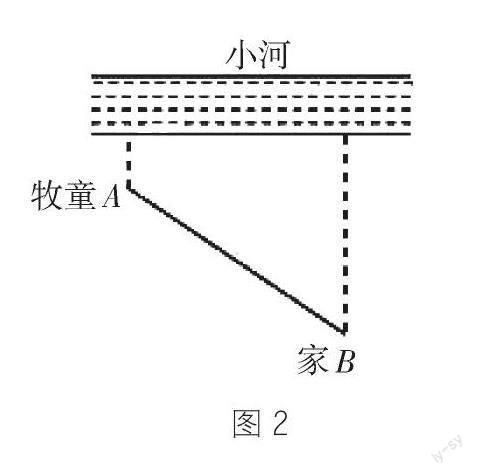
例：如圖2，一個牧童在距小河邊1千米的點A處放牛，河邊同側且距河邊7千米的點B處為牧童的家。已知點A與點B的直線距離是10千米，牧童想先把牛牽到河邊去飲水，然后再回家，求牧童要完成這件事情所走的最短路程是多少。

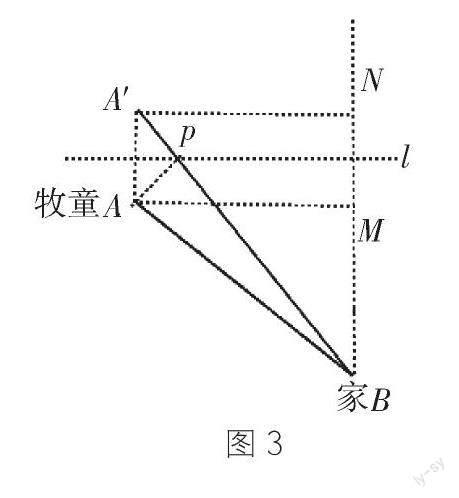
如果“河邊”用一條直線l表示，“牧童”用點A表示，“家”用點B表示，那么問題就轉化為學生熟悉的幾何模型——在直線l上找一個點P，使線段AP與PB之和為最小的數學問題。因此，利用兩點關于某條直線對稱的性質和勾股定理的知識可以解決。

本題以實際應用問題為背景，從“最短路程”問題中挖掘隱藏著的距離和最值的問題。學生必須以兩點關于直線對稱的性質為載體，將實際問題轉化為距離和最小模型，即兩邊之和的最小值問題。因三角形A′BA不是直角三角形（如圖3），可以進一步構造直角三角形，將問題轉化為已知直角三角形兩邊的長求第三邊的基本類型題。把實際問題轉化成若干個數學問題就是建模的思想，有利于培養學生的轉化思想，從而使思維更具靈活性、創造性。

三、建立概率與統計模型解決實際問題

為滿足時代的發展，概率與統計在日常生活中的應用越來越廣泛。數學教學應該服務于生活，應注重引導學生將所學概率與統計的知識應用于日常生活等方面，使新課標中提到的“用樣本估計總體”數學模型得到更充分地體現。

例：為了估計某一池塘的螃蟹數量，經常采用“抓、放、抓”的方法，即先抓上來n只螃蟹，分別打上標記，再放回去；如果在多次捕獲的螃蟹中，每a只中有b只有標記，則嘗試估算該池塘的螃蟹數量（用包含b、n、a的代數式表示）。

平時用樣本估計總體的試驗中，更多的是利用摸球的方式進行試驗。對于此種實際問題，學生較為生疏。教學中，教師可以通過平時學生最為熟悉的“摸球問題”進行類比，從而建立數學模型。

１.先從池塘中捉n只螃蟹，做好標記后，重新放回池塘，存在有標記和無標記兩種螃蟹——相當于在袋子中放有紅和白兩種球。

２.讓帶有標記的螃蟹完全混合于池塘——相當于把兩種球攪拌均勻。

３.再捕上來a只螃蟹——相當于在袋子中取出若干球作為樣本。

4.發現帶有標記的螃蟹只有b只——相當于取出樣本中紅色球的數目。

5. 樣本中有記號的螃蟹的百分比——相當于樣本中紅色球的百分比。

6. 估計池塘中有記號的螃蟹的百分比——相當于估計總體紅色球的百分比。

因此，此題可解答為：設該池塘中有螃蟹x只，則＝，解得x＝。

本題用生活中可能碰到的實際問題，提出了如何估計池塘中螃蟹的數量，激發了學生解決問題的欲望和學習的興趣。在解決此問題時，重在指導學生類比熟悉的模型，把未知關系轉為已知的關系，還可以先用數字表示，再到用字母代替數字，讓學生獲得對數學知識的理解與認同并掌握用樣本估計總體的數學模建，為以后解決新的問題打好基礎。

四、建立方程（組）模型解決實際問題

方程模型的題型有工程、增長率、利息和稅率、面積、分配等問題。解決此類型題，通常從分析問題的數量關系入手，設定未知數，運用定義、性質、定理、公式和已知條件、隱含條件，把實際問題中已知量和未知量之間的數量關系，轉化為方程（組）的數學模型，從而使問題得到解決，有利于提高學生創造性的思維能力。

例：某種病毒具有人傳人的特性，若一人攜帶相關病毒，若未實行有效隔離，經過研究，兩輪傳染后共有144人患上該種病毒（假設每輪傳染的人數基本相同）。問每輪傳染中平均每個人對應傳染了幾個人？

本題考查的是傳播問題，可以通過建立一元二次方程的數學模型解決問題。

五、建立不等式模型解決實際問題

在現實問題中，有許多問題很難確定具體的數值，這時教師可以通過問題中的等量和不等量關系列出不等式，可以求出或確定這一問題中某個量的變化范圍，從而對所有研究的實際問題有一個比較清楚的認識。這就是不等式模型。不等式建模題型有最佳方案、交通運輸、生產規劃、方案設計等。

數學建模可以從不同的角度分成很多不同的類型，想要更好地提高學生的數學建模意識，應該從日常生活中學生熟悉的問題入手，幫助歸納不同情況下的不同的模型和方法，讓學生在頭腦中形成一個數學建模的框架，從而提升學生的數學核心素養。

責任編輯 羅 峰