基于精細化建模的換熱管渦激振動數值研究
孫軍帥, 李旭鵬, 孫汝雷, 溫濟銘, 李小暢, 田瑞峰
(1.哈爾濱工程大學 核科學與技術學院, 黑龍江 哈爾濱 150001; 2.中國船舶及海洋工程設計研究院, 上海 200011; 3.哈爾濱工程大學 航天與建筑工程學院, 黑龍江 哈爾濱 150001)
核電站蒸汽發生器作為核電站關鍵設備,其安全性關乎核電站的安全運行。在長期運行中,蒸汽發生器換熱管極容易受流體作用而發生振動,當振動劇烈時,換熱管會與相鄰管束、支承結構等發生碰撞或摩擦,導致管束失效,造成巨大經濟損失[1],有必要對換熱管的流致振動現象進行深入研究。
大渦模擬方法(large eddy simulation, LES)在湍流計算方面具有優勢,隨著計算機技術的迅猛發展,具有較好的使用前景[2]。Lourenco等[3]較早地采用了粒子圖像測速法(particle image velocimetry, PIV)技術展開了Re=3 900的圓柱繞流研究。文獻[4-5]采用PIV技術對尾流區流場以及剪切層不穩定性等進行了研究。由于流場的湍流特性受實驗條件影響較大,且通過實驗研究能夠捕獲的流場信息極為有限,因此大量學者通過數值手段展開相關研究。Beaudan等[6]較早地采用LES方法對Re=3 900的圓柱繞流問題進行了數值模擬。Kravchenko等[7]基于B樣條方法的高精度LES方法,研究了Re=3 900圓柱繞流問題,通過與實驗結果[3]對比發現,實驗可能存在環境干擾從而導致了剪切層較早轉捩。Parnaudeau等[5]除了進行了實驗研究外,同樣采用LES方法展開了數值研究。戰慶亮等[8]、端木玉等[9]采用LES方法研究了Re=3 900時圓柱繞流流場特性,通過對比研究驗證了計算程序在湍流場計算的準確性。一些關鍵流場參數方面仍存在一定的爭議,這可能是由于實驗技術差異以及數值計算模型不同導致的。
單根換熱管流致振動從流致振動機理來說,本質上屬于單圓柱渦激振動的范疇。文獻[10-13]對圓柱渦激振動進行了系統性的實驗研究。文獻[14-15]在研究低質量阻尼參數的雙自由度圓柱渦激振動時發現:當質量比m*=2.6時,橫向振動響應幅值會產生“超級上端分支”,并出現了“2 T”形態的尾跡模式。Kang等[16]、Li等[17]基于RANS法建立了雙自由度圓柱渦激振動問題的二維計算模型,但由于二維模型忽視了流場在高雷諾數時具有高度三維化渦體結構,導致得到的最大橫向振幅和“超級上端分支”的范圍與實驗結果存在一定的偏差。Gsell等[18]和Li等[17]分別采用直接數值模擬(direct numerical simulation,DNS)方法和LES方法建立了雙自由度圓柱渦激振動問題的三維計算模型以模擬“超級上端分支”,但結果還是均低于實驗值;同時,由于計算工況較少,無法對該問題進行較好描述。
綜上所述,在單圓柱渦激振動問題上,主要存在以下問題:1)在流場計算方面,CFD模型存在差異,導致關鍵流場參數存在著一定爭議;2)在振動響應計算方面,不論建立的計算模型是二維還是三維的,計算結果均與Jauvtis &Williamson[15]的實驗值存在較大差異,體現在超級上端分支范圍、最大橫向振幅、運動軌跡等方面。
本文基于LES方法建立了精細化流場計算模型,以雷諾數為3 900的固定圓柱繞流為例,進行了網格敏感性分析,而后通過不同求解方法的對比研究選取HHT-α方法求解結構動力學方程,最終結合局部動網格變形技術,建立了換熱管渦激振動流固耦合計算模型,并對Jauvtis &Williamson[15](簡稱為J-W)的經典渦激振動實驗的振動響應進行了預測。
1 流固耦合計算模型
1.1 大渦模擬控制方程
LES方法最早是由氣象學家Smagorinsky[19]提出的,其主要思路是對N-S方程進行濾波處理,將湍流中渦分為大尺度渦和小尺度渦2種,對大渦直接計算,對小渦進行模擬。對于不可壓縮流動,濾波后的N-S方程為:
(1)
(2)
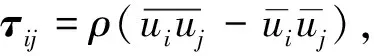
亞格子應力模型有很多形式[19-21],本文采用了WALE模型[21],該模型通過考慮湍流壁面及動量傳遞效應等,保證了對近壁面流域模擬的準確性。同時,采用SIMPLEC方法求解壓力速度耦合方程,采用二階隱式方法對時間項進行離散求解。
1.2 結構動力學模型
將單根換熱管簡化為剛性圓柱,并采用雙自由度的質量-阻尼-彈簧模型對換熱管渦激振動力學模型進行描述,則流向和橫向的控制方程分別為:
(3)
(4)

對上述方程采用HHT-α方法[22]進行求解,該方法比傳統的Runge-Kutta方法和Newmark-β方法具有更優的算法穩定性和數值耗散性能等。以式(4)為例,進行方程推導:
(1-η)kyt+Δt+ηkyt=(1-η)Fdt+Δt+ηFdt
(5)
(6)
(7)

最終得到關于yt+Δt的方程:
(8)
其中:

(9)
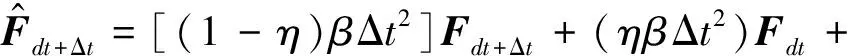
(10)
由式(8)可得:
(11)
將式(6)~(11)編寫成C語言程序,以實現單根換熱管渦激振動計算中對結構動力學部分的求解。
1.3 幾何模型
在固定圓柱繞流計算和單根換熱管渦激振動計算中,坐標原點位于換熱管中心,流向為x坐標,橫向為y坐標,展向為z坐標。二者計算域的相對大小相同,但直徑D不同。換熱管渦激振動計算的計算域如圖1所示,寬為20D,長為30D。基于文獻[4,7,9,23]對不同展向長度的圓柱繞流問題進行的研究,選取展向長度為πD。圓柱距離入口10D,距離上下邊界10D。入口為均勻速度入口條件,上下邊界以及展向的前后邊界均為對稱邊界,出口為壓力出口,圓柱表面為無滑移壁面。
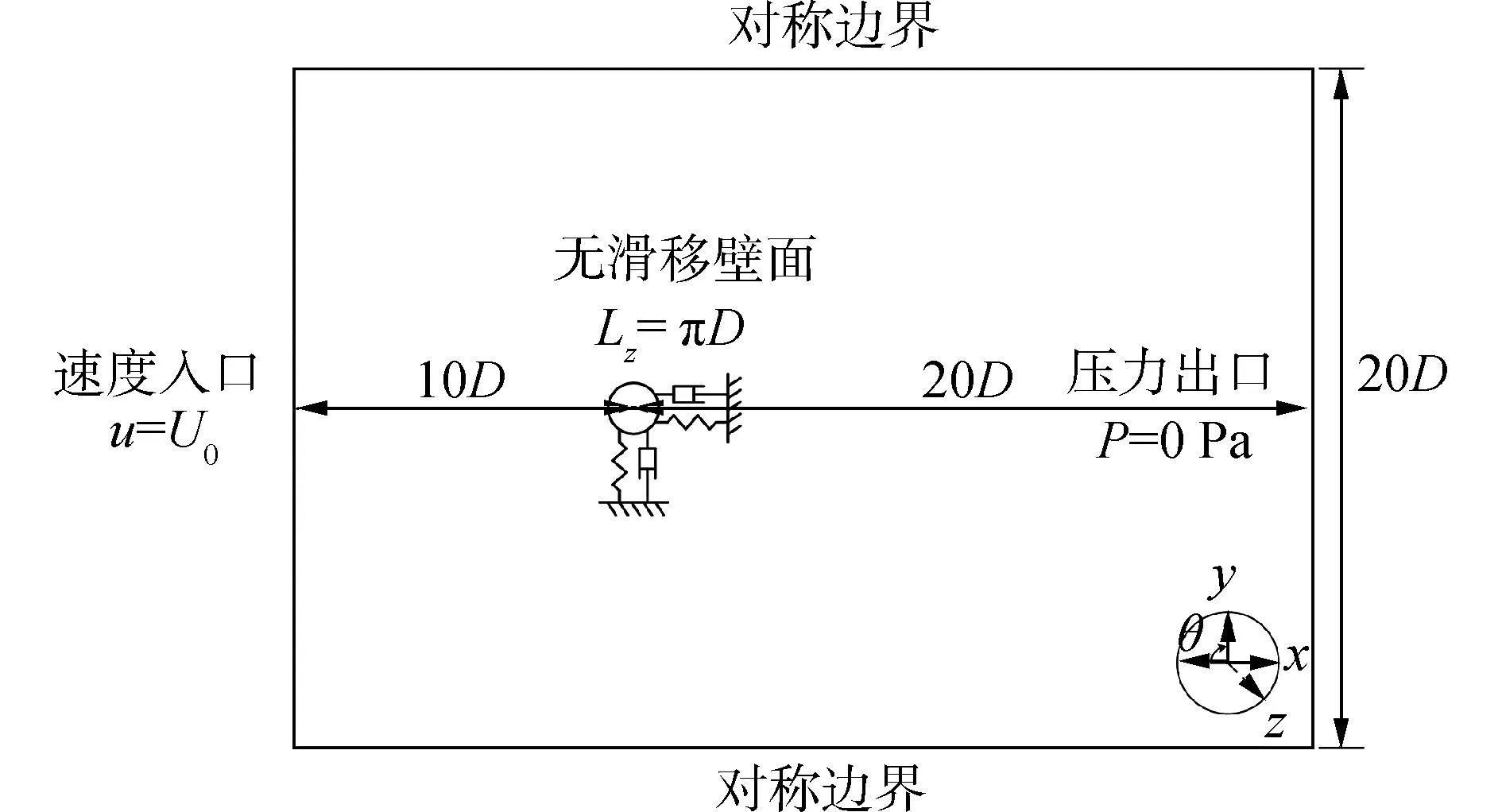
圖1 渦激振動計算的計算域示意Fig.1 Schematic diagram of the computational domain for vortex-induced vibration calculation
2 網格敏感性分析

表1 敏感性分析的網格模型設置參數

圖2 G3網格模型xoy截面示意Fig.2 Schematic diagram of the xoy section of G3 model
為了得到圓柱繞流問題的合理統計數據,根據Franke等[24]的研究,統計時間應大于40個漩渦脫落周期,因此本文的總計算時間約為100個漩渦脫落周期,選取穩定后的70個漩渦脫落周期數據作為有效數據進行統計。
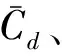
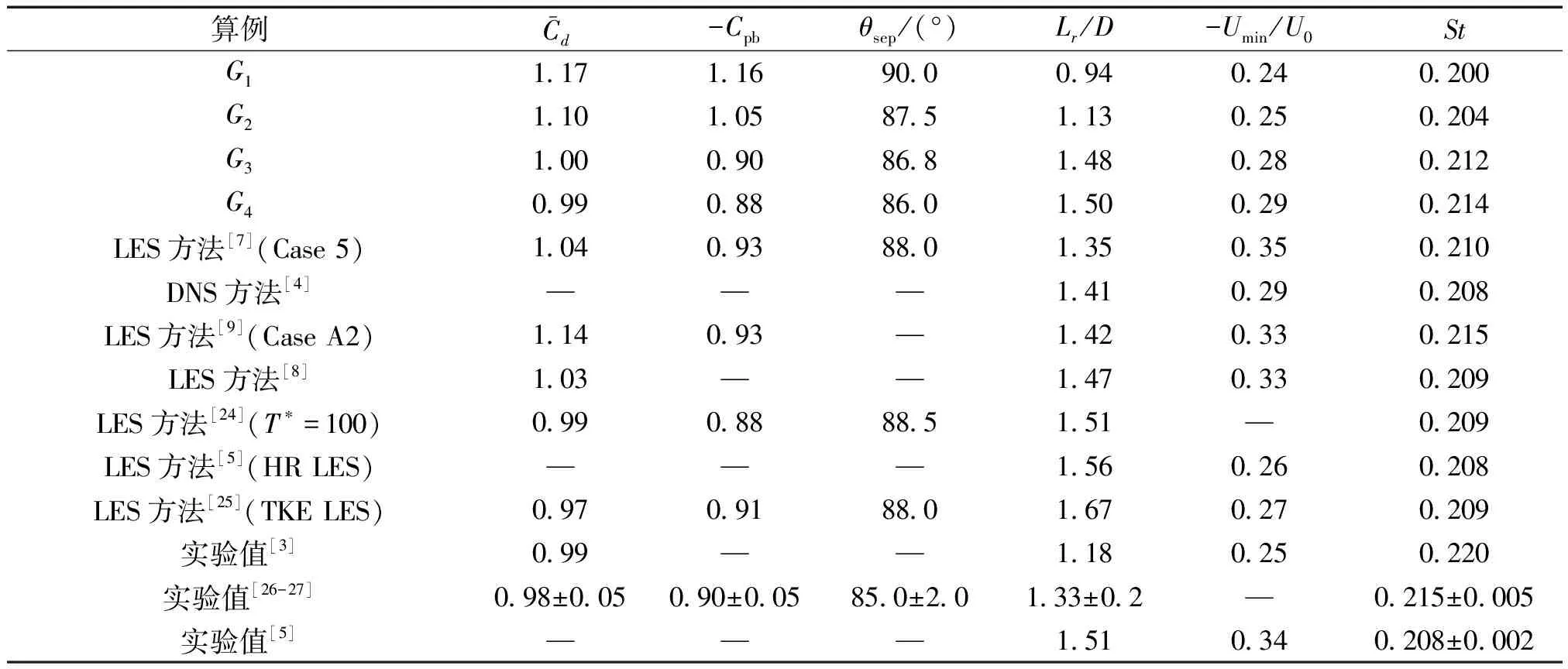
表2 網格敏感性分析結果對比Table 2 Comparison of grid sensitivity analysis results
4套網格的圓柱表面時均壁面速度梯度系數與實驗數據[28]的對比如圖3所示。壁面速度梯度系數VG定義為VG=|ζ|/Re0.5,|ζ|為無量綱速度梯度的絕對值。可以看出,4套網格的時均壁面速度梯度系數變化均呈現先增后減的趨勢,并在θ約為50°處取得極大值,其中分離點為曲線與橫軸交點,隨著網格數量的增加,分離點逐漸收斂,曲線也逐漸收斂于實驗數據,參數θsep逐漸收斂。但需要注意的是,在θ為180°處,計算得到的時均壁面速度梯度系數約為0,明顯小于實驗數據[28]。由于圓柱繞流尾渦交替脫落,θ為180°處的瞬時壁面速度梯度系數應呈現周期性變化,作時均處理后其值應近似為0,驗證了計算的正確性以及數據統計處理的合理性。
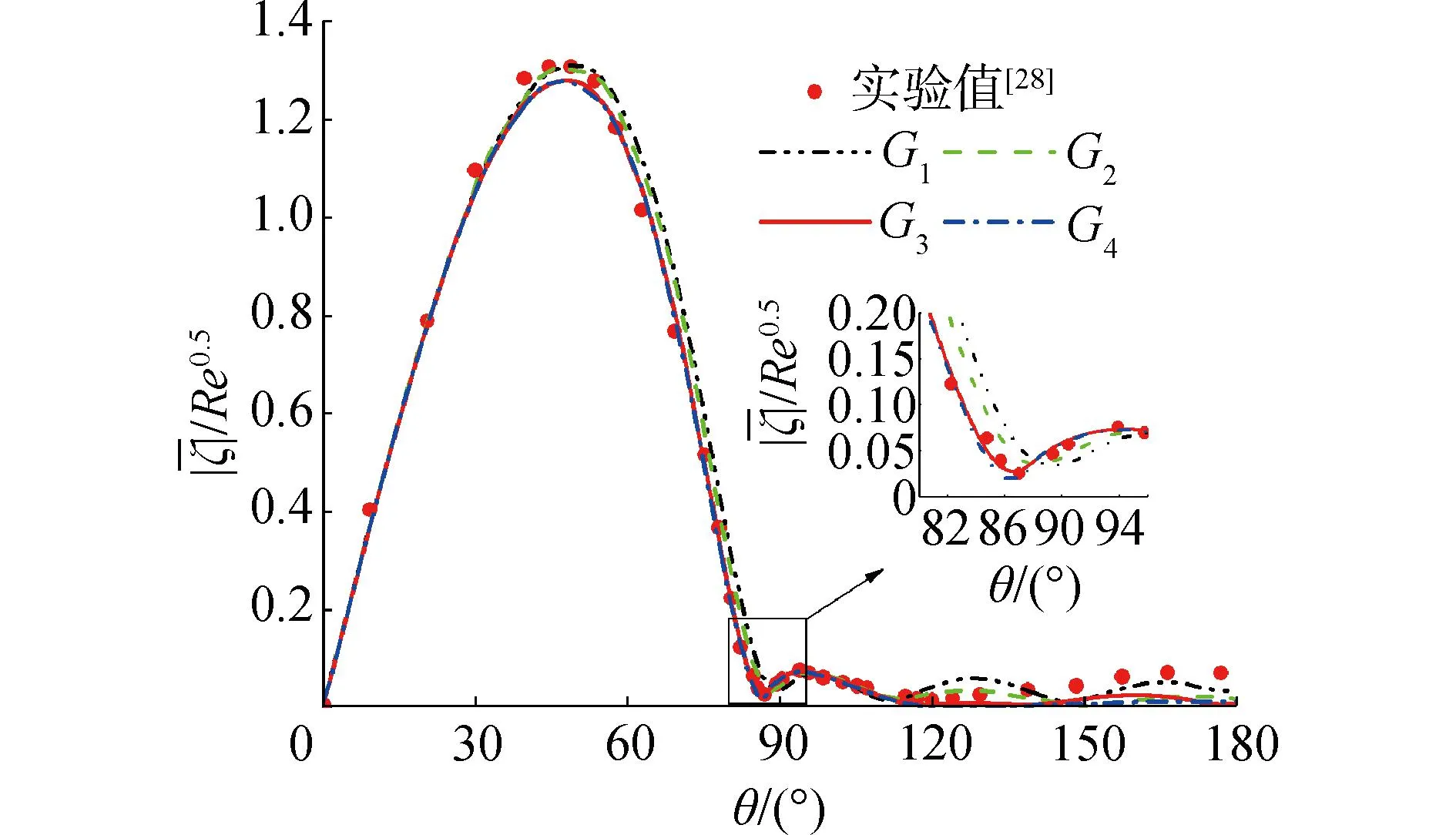
圖3 不同網格模型時均壁面速度梯度系數分布Fig.3 Time-averaged wall velocity gradient coefficient distributions for different grid models
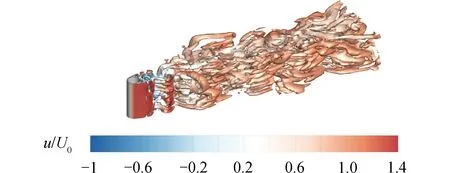
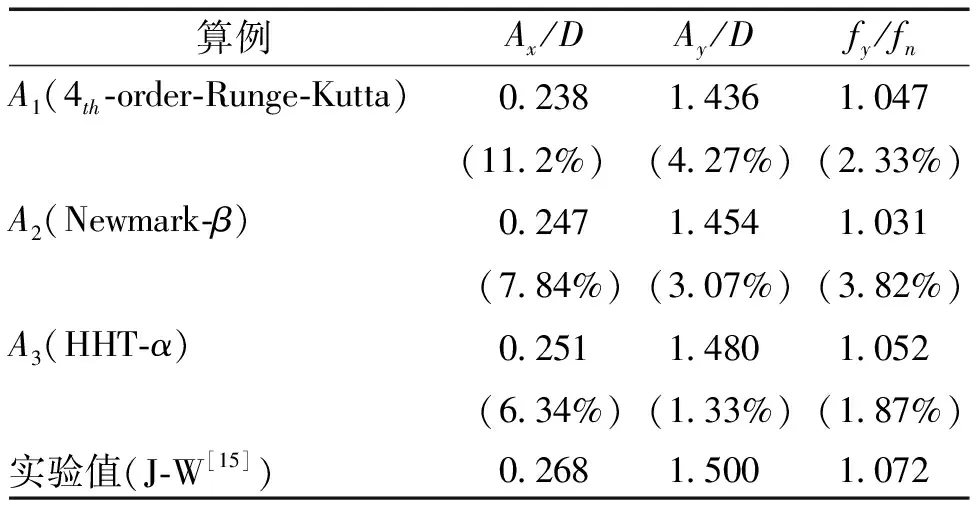
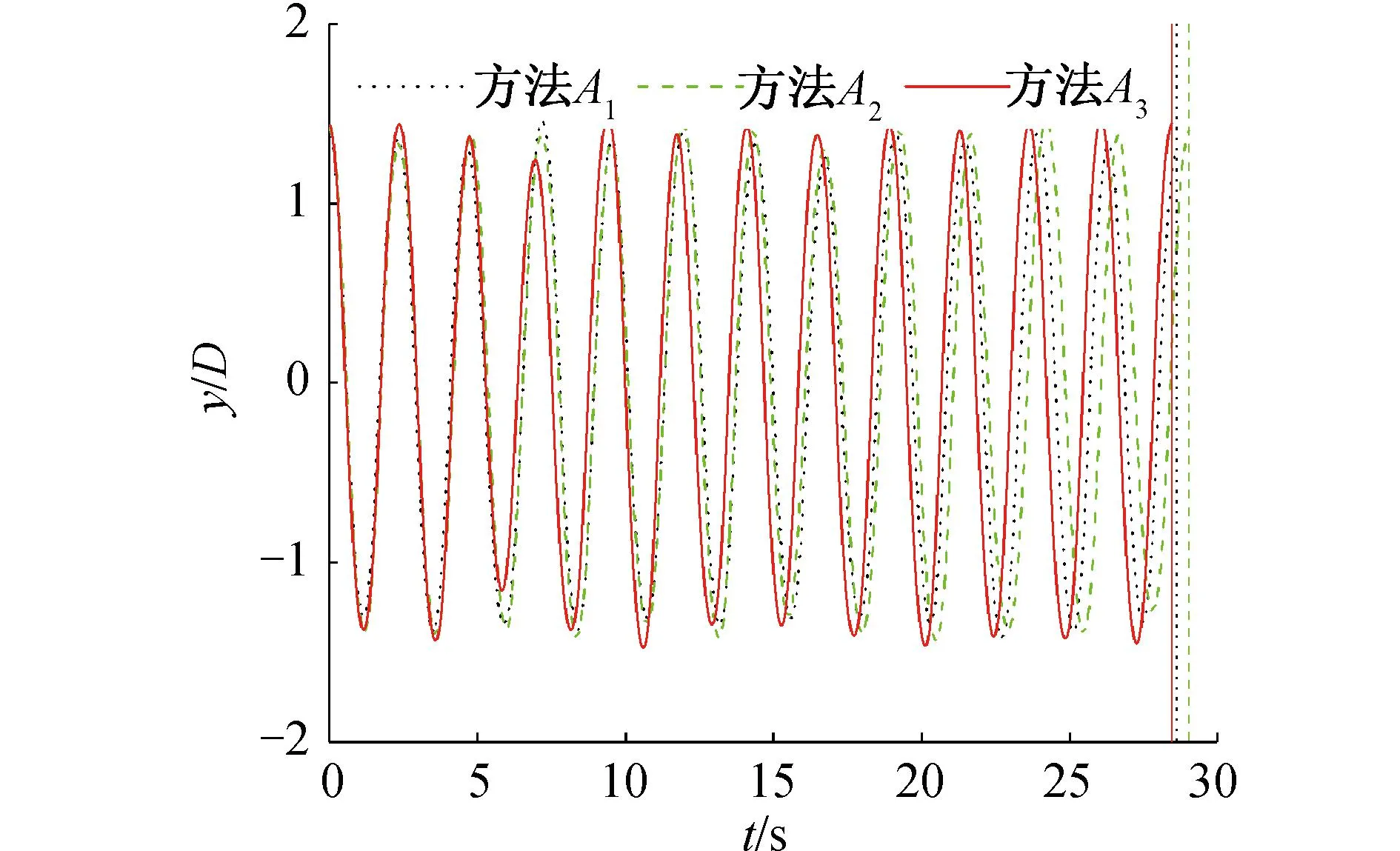
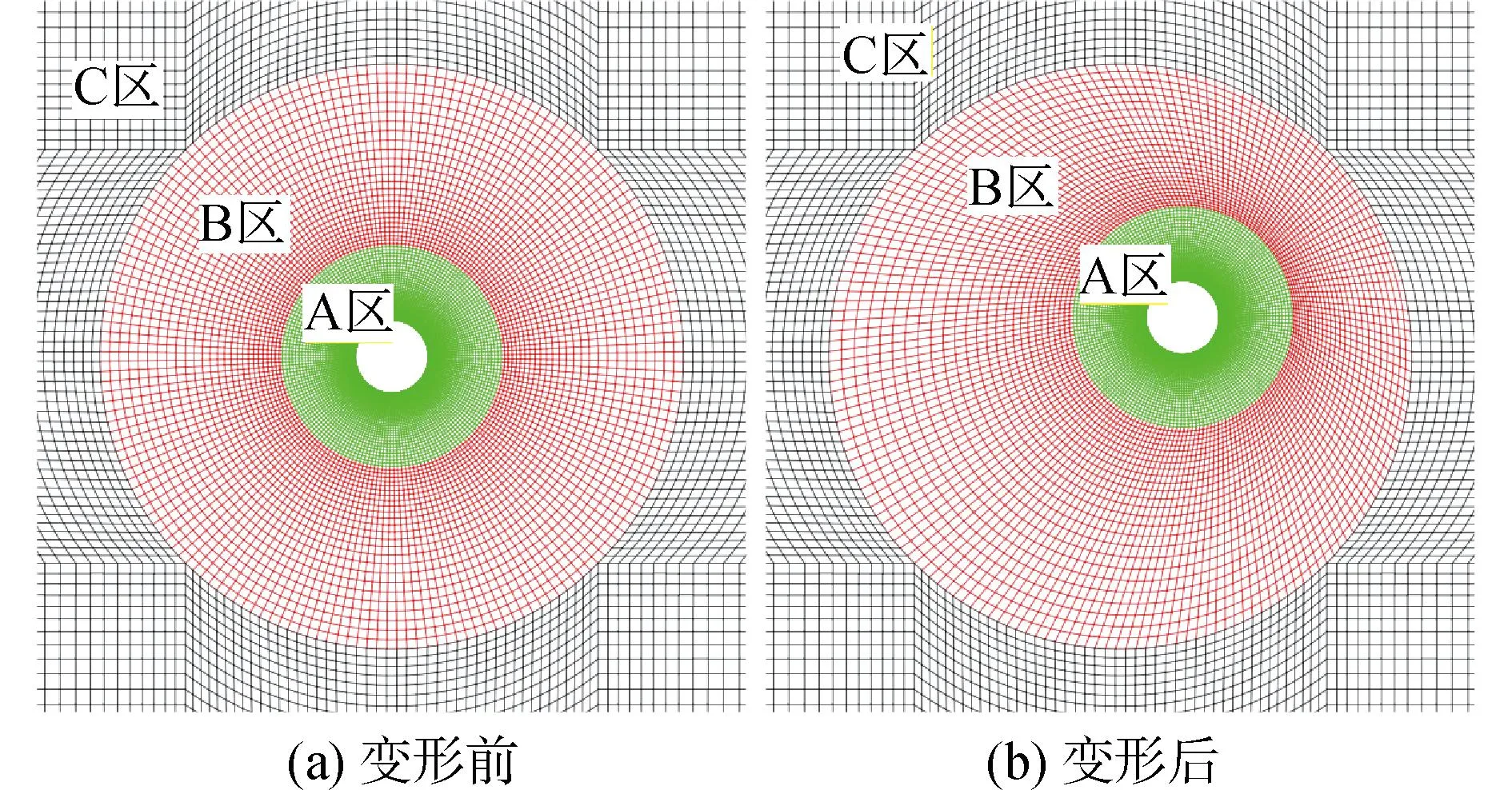
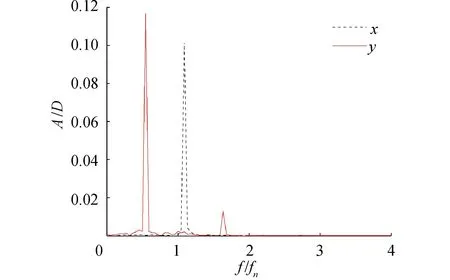
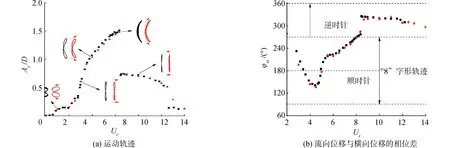
4套網格的圓柱尾流區不同截面時均流向速度分布與相關實驗數據[3,5,29]及數值結果[5]的對比如圖4所示。為了將不同截面時均流向速度分布進行對比,對各個截面的數據進行了偏移處理。可以看出,時均流向速度分布由近尾流區(x/D<3)的“U”型向遠尾流區(3 圖4 不同網格模型圓柱尾流區不同截面時均流向速度分布Fig.4 Time-averaged streamwise velocity distributions of the centerline beyond cylinder for different grid models 圖5給出了G3網格模型的圓柱繞流瞬時流場渦量,圖中的渦量等值面采用Q準則[30]表示,用無量綱流向速度u/U0進行染色。可以看出,Re=3 900的圓柱繞流問題具有豐富的流動結構,顯示出復雜的漩渦脫落現象。同時,附著在圓柱壁面的剪切層呈現二維結構,而分離區和尾流區呈現出高度三維化的渦體結構,具有明顯的湍流特征。 圖5 圓柱繞流瞬時三維渦量等值面圖(Q=10)Fig.5 Isosurface diagram of instantaneous 3D vorticity of flow around a cylinder (Q=10) 綜上所述,對圓柱繞流問題而言,近尾流區流動情況復雜,特別是回流區對網格的要求較高,粗網格會導致剪切層較早分離,回流區長度變短,速度型提前由“U”型轉變為“V”型;而遠尾流區對網格要求較低,不同網格的速度型與實驗值吻合較好,僅在峰值處存在誤差。也就是說,近尾流區流場對網格更敏感,因此需要對近尾流區的網格進行加密,才能準確地模擬圓柱繞流現象。因而,認為G3可以準確地模擬圓柱繞流現象,并且滿足網格無關性要求,則后續工作將基于G3網格模型開展。 表3 不同求解方法的對比Table 3 Comparison of different methods 振幅響應反映的是算法的耗散性能,即算法導致的能量衰減程度。Kane等[31]的研究表明,隨著計算時間的延長,Newmark-β類方法的能量衰減要明顯小于四階Runge-Kutta方法。本質上HHT-α方法是由Newmark-β方法衍生而來,具有更優的數值性能。這直接導致方法A3計算得到的振幅響應更接近實驗值,而方法A2次之,方法A1最次。 頻率響應反映的是算法的彌散性能,即算法導致的周期延長程度。選取了12個振動周期的橫向位移y/D的時程變化曲線,起始時刻相位相同,3種計算方法的對比如圖6所示。可以看出,隨著計算時間的延長,誤差逐漸積累導致方法A1和方法A2的振動周期延長,與方法A3相比,方法A1計算的振動周期延長了6.60%,方法A2計算的振動周期延長了23.2%。也就是說,在長時間進行計算時,方法A1和方法A2將會帶來較大的計算誤差,最終導致計算結果會偏離物理事實。因此,最終選取方法A3(HHT-α方法)對換熱管渦激振動計算中結構動力學部分進行求解。 圖6 不同計算方法的橫向位移y/D的時程變化曲線Fig.6 Time-history curves of transverse displacement y/D for different methods 基于建立的換熱管流致振動流固耦合計算模型對單根換熱管渦激振動問題進行計算,計算參數與J-W的實驗參數保持一致。圓柱直徑D=0.038 1 m,質量比m*=m/md=2.6,質量阻尼參數(m*+ca)ζ=0.013,水中固有頻率fn=0.4 Hz,工質為水,根據實驗數據推算出流體密度ρ=995.4 kg/m3,動力粘度μ=0.000 781 Pa·s。時間步長Δt取為0.005 s,保證每個結構固有周期包括大約500個時間步。計算工況為2 考慮到計算中圓柱周圍網格需要吸收圓柱邊界的運動,采用局部動網格變形技術處理網格變形。對圓柱周圍直徑為8D范圍內采用O形網格進行網格加密,將其內側直徑為3D范圍的網格設置為剛體網格區域(A區域),剩余部分的網格設置為變形網格區域(B區域);加密區以外的網格設置為靜止網格區域(C區域)。變形前后的網格如圖7所示,可以看出,采用局部動網格變形技術變形后的網格具有較好的網格拓撲結構,網格質量較高,不會出現“負體積”現象,可以保證計算的有效進行。同時,由于只有變形網格區域的網格參與變形計算,可以大大節省計算資源。 圖7 xoy截面變形前后的網格Fig.7 Grid of the xoy section before and after deformation 3.2.1 振動響應 將不同折算流速下渦激振動響應(橫向和流向振幅響應、橫向振動頻率響應)與J-W[15]的實驗數據以及Li[17]和Gsell[18]的計算結果進行對比,如圖8所示。可以看出,計算得到的橫向振幅和流向振幅與實驗數據吻合較好,并且計算結果要優于Li和Gsell的計算結果,計算可以成功捕捉到實驗中的初始分支、超級上端分支以及下端分支,各個分支的折算流速范圍與實驗吻合較好,其中超級上端分支最大橫向振幅為1.48D,略小于J-W的實驗值1.50D,對應的折算流速Ur為8.35,與實驗值更為接近。橫向振動頻率響應也存在著明顯的3個分支,分別與初始分支、超級上端分支和下端分支相對應,且與實驗數據吻合較好。3個分支間以“跳躍”的方式過渡,這種過渡方式與實驗變化趨勢相同。需要說明的是,在某些折算流速下,橫向振動可能存在多頻現象,這里只選取了橫向振動主頻。 圖8 不同折算流速下振動響應對比Fig.8 Comparison of vibration response at different reduced velocities 當折算流速較小時,流向振幅和橫向振幅相對較小,但在2 圖9 Ur=3時流向和橫向振幅頻譜圖Fig.9 Spectrogram of streamwise and transverse amplitude at Ur=3 隨著折算流速的增大,橫向振幅逐漸增大,但流向振幅逐漸減小。當Ur>4時,振動逐漸進入鎖定區間,流向振幅和橫向振幅逐漸增大,橫向振動頻率由漩渦脫落頻率逐漸趨近于圓柱水中固有頻率。在Ur=5時,橫向振幅明顯增大,振動進入超上端分支。在超上端分支區間5 當Ur>8.65時,橫向振幅和流向振幅迅速減小,振動進入下端分支,橫向振動頻率跳躍至第3頻率分支,該頻率分支的頻率與圓柱在空氣中固有頻率相近。在整個下端分支區間8.65 3.2.2 運動軌跡 本文對不同折算流速下渦激振動的運動軌跡進行研究,將計算得到的運動軌跡與實驗數據進行對比,如圖10所示。運動軌跡左為實驗值[15],右為本文計算值。對計算得到的運動軌跡進行縮放處理,但整體形狀不發生改變。可以看出,計算得到的運動軌跡形狀以及流向位移與橫向位移的相位差φxy與實驗數據吻合較好。 圖10 運動軌跡以及流向與橫向位移的相位差對比Fig.10 Comparison of motion trajectory and phase difference between streamwise and transverse displacement 當振動處于初始分支和超級上端分支時,運動軌跡為順時針方向;而當振動進入下端分支時,運動軌跡轉變為逆時針方向。在Ur=2時,運動軌跡類似于一條橫線,這是因為此時橫向位移較小而流向位移較大。隨著折算速度的增加,橫向振幅和流向振幅均逐漸增大,在Ur=3時,流向振動處于鎖定狀態,二者振幅相當,并且流向振動頻率約為橫向振幅的2倍,運動軌跡表現為標準“8”字形。當振動進入超級上端分支區間,橫向振幅和流向振幅繼續增大,但橫向振幅的漲幅明顯大于流向振幅,振動軌跡形狀逐漸由瘦長“8”字形向傾斜“8”字形轉變。當Ur=7.5時,流向振幅達到最大值,隨著折算流速的繼續增加,流向振幅開始逐漸減小,而橫向振幅卻繼續增大,振動軌跡形狀持續變化。當Ur=8.35時,運動軌跡轉變為新月形。當振動進入下端分支時,橫向振幅和流向振幅均驟減,但橫向振幅要大于流向振幅,運動軌跡又逐漸變為“8”字形,但此時運動軌跡為逆時針方向。 3.2.3 尾跡模式 選取xoy截面(z=0),對渦激振動尾跡模式進行研究,圖11給出了不同折算流速下的尾跡模式,其中Ωz為z方向渦量,定義為Ωz=?v/?x-?u/?y。 圖11 不同折算速度下尾跡模式對比Fig.11 Comparison of wake mode at different reduced velocities 可以看出,渦激振動尾跡模式分為“SS”模式、“2S”模式、“2T”模式和“2P”模式。當Ur=2時,由于橫向振幅較小,而流向振動占主導地位,振動處于“SS”分支,每個振動周期內圓柱后側脫落一對對稱的反向漩渦,與Jauvtis等[14]進行的可視化實驗結果相同。隨著折算流速的增加,尾跡模式發生轉變,當Ur=3時,每個振動周期內圓柱兩側交替脫落方向相反的2個漩渦,該泄渦模式被稱為“2S”模式。 當折算流速繼續增大時,振動逐漸進入超級上端分支,在這過渡區間上,尾跡模式由“2S”模式向一種新的泄渦模式“2T”模式轉變,即每半個振動周期內圓柱一側脫落3個漩渦,其中一個漩渦的強度遠小于另外2個漩渦的強度,且2個強度較大的漩渦方向相同,如圖11(c)所示。當振動完全處于超級上端分支時,尾跡模式完全轉變為“2T”模式,如圖11(d)和(e)所示。當振動進入下端分支時,尾跡模式發生轉變,在每半個振動周期內圓柱一側脫落一對方向相反強度相近的漩渦,稱為“2P”模式。 1)在進行固定圓柱繞流問題計算時,圓柱近尾流區(x/D<3)流動參數對網格較為敏感,粗網格會使剪切層提前轉捩,導致回流區長度變短,而圓柱遠尾流區(3 2)與傳統的Runge-Kutta方法和Newmark-β方法相比,本文采用的HHT-α方法在求解結構動力學方程上更具優勢,體現在較低的數值耗散、較小的數值彌散以及較高的數值精度,使得計算得到的振幅和振動周期更貼近實驗數據。 3)在渦激振動計算中,與其他學者的結果相比,本文建立的渦激振動計算模型可以準確預測雙自由度圓柱渦激振動行為,計算可以成功捕捉到初始分支、超級上端分支和下端分支,以及相應的“SS”、“2S”、“2T”以及“2P”尾跡模式,超級上端分支范圍和最大橫向振幅以及不同分支間的過渡方式與實驗數據一致。 由于換熱管主要以管束的形式存在于蒸汽發生器中,在今后的工作中,可以將本文建立的精細化換熱管渦激振動流固耦合模型應用于管束結構流致振動計算中,以支持蒸汽發生器管束結構的設計與優化工作等。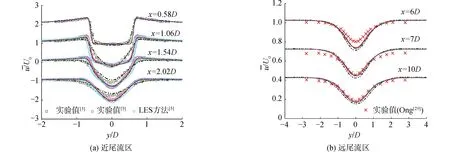
3 換熱管渦激振動計算
3.1 結構動力學方程求解方法對比研究
3.2 單根換熱管渦激振動計算


4 結論

