基于中子均方位移守恒的平均散射角余弦計算

秦帥, 李云召, 賀清明, 曹良志, 吳宏春

(西安交通大學 核科學與技術學院,陜西 西安 710049)

兩步法[1]是核反應堆物理工程計算中常用的計算方法,其計算精度取決于輸運計算產生的均勻化群常數是否可靠。根據均勻化理論[2],均勻化前后應保證積分反應率守恒和泄漏率守恒,其中,考慮均勻化區域的各向異性散射是實現泄漏率守恒的關鍵條件。目前的兩步法計算中,一般使用2類方法:1)產生均勻化區域的高階散射截面,并用于堆芯輸運計算中;2)產生均勻化區域的擴散系數,并用于堆芯擴散計算中。其中,擴散系數的精確計算一般需要用到高階散射截面[3]。因此,產生精確的高階散射截面是考慮均勻化區域各向異性散射的基礎。

蒙特卡羅輸運計算方法[4]幾何處理能力強,基于連續能量模擬,可以直接考慮共振效應,計算精度很高,已在均勻化群常數的產生中得到了一定應用[5-8]。但是,蒙特卡羅方法在計算高階中子通量矩時統計漲落很大,一般以中子標通量為權重計算平均散射角余弦,帶來計算誤差[6]。使用蒙特卡羅方法計算的高階散射矩陣,在快中子反應堆問題中引起的有效增殖因子計算偏差達到500×10-5～600×10-5[9]。

本文提出一種基于中子均方位移守恒的平均散射角余弦計算方法,稱為中子均方位移守恒法。因為計算平均散射角余弦的主要目的是保證均勻化區域泄漏率守恒,而中子的泄漏直接取決于中子在均勻化區域內的均方位移。該方法在蒙特卡羅輸運計算過程中對中子均方位移進行統計,在得到中子均方位移后,計算得到使其守恒的平均散射角余弦。基于西安交通大學核工程計算物理實驗室自主開發的蒙特卡羅粒子輸運計算程序NECP-MCX[10]對該方法進行了實現,并使用各向異性較強的快中子反應堆問題對該方法進行了數值測試,驗證了其計算精度。

1 中子均方位移守恒法理論模型

1.1 高階散射截面與平均散射角余弦

高階散射截面是將散射角的分布使用勒讓德函數進行展開的系數矩,其定義為:

(1)

式中:r為空間變量;μ為散射角余弦;g′為入射能群;g為出射能群;Σs, g′→g(r,μ)為空間r處,以散射角余弦為μ,由g′群散射至g群的散射截面;Σs,g′→g(r)為空間r處,由g′群散射至g群的散射截面;Σs,n,g′→g(r)為空間r處,由g′群散射至g群的n階散射截面;fn,g′→g(r)為對應能群下散射角余弦分布函數的n階矩;Pn(μ)為n階勒讓德函數;N為展開階數。

散射角余弦分布函數的n階矩為:

(2)

式中:E′和E分別為中子入射能量和出射能量;Eg′和Eg為能群g′和g的能量下界;φn(r,E′)為空間r處能量為E′的n階中子通量矩;fn(r,E′,E)為空間r處,能量由E′散射至E的散射角余弦分布函數n階矩,其計算公式為:

(3)

式中:f(r,E′,E,μ)為空間r處,中子以散射角余弦μ,能量由E′轉移至E的概率。

根據式(1)～(3),可以得到各階散射截面。對于大多數反應堆問題,一般取展開階數為1,一階散射截面可以寫為:

(4)

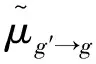
(5)

式中φ1(r,E′)為空間r處能量為E′的一階中子通量矩。

由式 (5)可以看出,精確的平均散射角余弦計算應以一階中子通量矩為權重,計算其分布函數的一階矩,但在蒙特卡羅輸運計算過程中,不同飛行方向的中子會發生相互抵消,導致一階中子通量矩的統計漲落很大。因此,在傳統計算中一般采取通量正比假設[11]:

φn(r,E′)=Cnφ(r,E′)

(6)

式中:φ(r,E′)為空間r處能量為E′的中子標通量;Cn為n階對應的常數。

根據式 (6),可以直接用中子標通量代替式 (5)中的一階中子通量矩,避免統計漲落過大的問題。但中子通量和一階中子通量矩并不滿足通量正比假設,從而引入了計算誤差。

1.2 中子均方位移與平均散射角余弦

計算高階散射截面和平均散射角余弦的主要目的是考慮中子的各向異性散射過程,最終影響中子在均勻化區域內的直線飛行距離。因此,可以根據中子均方位移守恒,計算中子的平均散射角余弦,從而避免一階中子通量矩的計算。

1.2.1 中子均方位移計算[12]

首先,考慮單能中子在無限大均勻介質內飛行的情況。將中子由當前位置移動到下個碰撞點的過程稱為中子的一次飛行,那么中子每次飛行長度l的概率分布函數p(l)滿足:

p(l)dl=Σte-Σtldl

(7)

式中Σt為均勻介質的總截面。

中子在若干次飛行后的均方位移可以表示為:

(8)

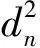
根據向量運算,式(8)為:

(9)

根據式 (7),式(9)中右端第1項可以寫為:

(10)

式中λ為平均自由程,λ=1/Σt。

式 (9)中右端第2項可以寫為[12]:

(11)

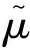
最終,中子在n次飛行后的均方位移可以表示為:

(12)

當飛行次數確定后,中子均方位移是平均散射角余弦的函數。一般情況下,該函數在[-1, 1]單調增長,即中子平均散射角余弦越大,中子在發生碰撞后越傾向于向前飛行,其均方位移就越大。

1.2.2 平均散射角余弦的計算

根據1.2.1節的推導,基于中子均方位移守恒,平均散射角余弦的計算方法為:

1)中子經由源抽樣或碰撞后進入能群g,記錄其當前位置為rg,s,設置ng=0,wg=0;

2) 模擬中子輸運至rg,c處發生碰撞,更新該中子在當前能群的碰撞次數ng=ng+1;

3) 為處理隱俘獲,更新該中子的碰撞權重wg+1=wg+wi(wi為碰撞前的中子權重);

4) 檢查中子的出射能群,若中子能群不發生改變,則回到步驟2),若中子能群發生改變或被殺死,則更新計數Ng(ng)=Ng(ng)+Wg/ng及均方位移計數Dg(ng)=Dg(ng)+|rg,c-rg,s|2·Wg/ng;

5) 若中子仍存活或已模擬中子數未達到設定值,回到步驟1),否則退出。

全部模擬結束后,不同碰撞次數下的中子均方位移為:

(13)

式中Nc為用戶設定的最大飛行次數。

得到中子均方位移后,即可根據式 (12)搜索得到均勻化區域的平均散射角余弦。

需要注意,式 (12)基于無限大介質得出的,但是,在兩步法計算中,經常需要計算有限幾何區域的均勻化群常數。針對這種情況,本文采取的修正方法為基于該有限幾何區域的材料布置建立無限大問題,然后使用通量正比假設和本文方法分別計算無限大問題的平均散射角余弦,并計算修正因子:

(14)

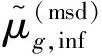
(15)

另外需要注意,本文計算的平均散射角余弦僅對各群自散射截面進行修正,這是因為中子發生各向異性散射時,其能量損失相對較少,更易發生在自散射中,因此僅對自散射截面進行修正即可有效改善計算精度。最終的一階自散射截面計算公式為(忽略空間項):

(16)

2 中子均方位移守恒法數值測試

為了驗證本文方法,基于蒙特卡羅粒子輸運計算程序NECP-MCX開發了相應的中子均方位移統計功能。NECP-MCX為西安交通大學核工程計算物理實驗室自主開發的蒙特卡羅粒子輸運計算程序,已具備均勻化計算功能并在“華龍一號”啟動物理試驗中進行了驗證[8]。

2.1 一維問題

首先基于文獻[9]中的一維問題對本文方法進行測試,該問題來自文獻[13]中設計的低濃鈾鈉冷快堆,為簡化問題,對燃料區和反射層進行了打混。問題幾何如圖1所示,燃料區和反射層的核素組成如文獻[9]所示。

圖1 一維問題布置圖Fig.1 Layout of one-dimensional problem

本文使用NECP-MCX連續能量模式計算參考解,并在求解過程中分別統計燃料區和反射層區的33群均勻化群常數(能群結構見表1),其中一階散射截面基于通量正比假設得到。計算時共投入1 050代,其中前50代為非活躍代,每代投入50萬個粒子。之后,使用中子均方位移守恒法分別計算了燃料和反射層的平均散射角余弦及修正因子,并對一階自散射截面進行修正。最后,分別使用修正和未修正的一階散射截面對該問題進行NECP-MCX多群計算。

實驗室利用Axis PTZ相機，通過圖像檢測Rovio的像素重心，然后由坐標變換函數轉化為攝像頭姿態(pan,tilt)。通過支持向量機算法間接實現(pan,tilt)和固定坐標系(x,y)的轉換。具體定位步驟如下：

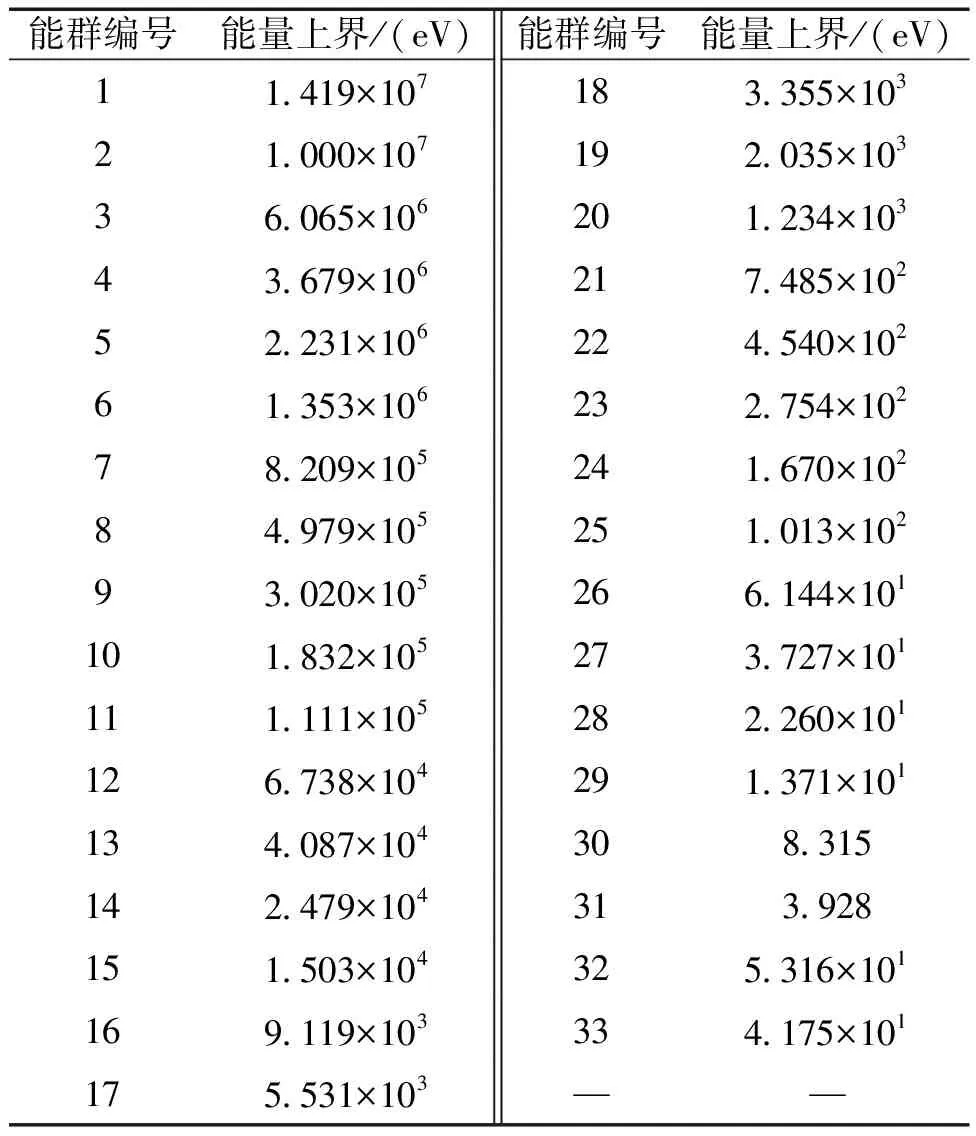
表1 33群能群結構Table 1 Structure for 33-group

表2中給出了一維問題有效增殖因子keff的計算結果,參考解為1.147 18±0.000 03。可以看出,使用通量正比假設時,由于低估了系統的各向異性,多群計算的keff較大,使用本文方法對一階散射截面修正后可以有效改善多群計算結果。

表2 一維問題有效增殖因子計算結果

圖2為一維問題的中子通量分布比較。由于低估了各向異性,通量正比假設計算的反射層區域通量較大,而使用修正截面的計算結果則與參考解符合較好。圖3中給出了一維問題的中子通量相對偏差分布,修正方法將通量的最大相對偏差由9%降低為4%。

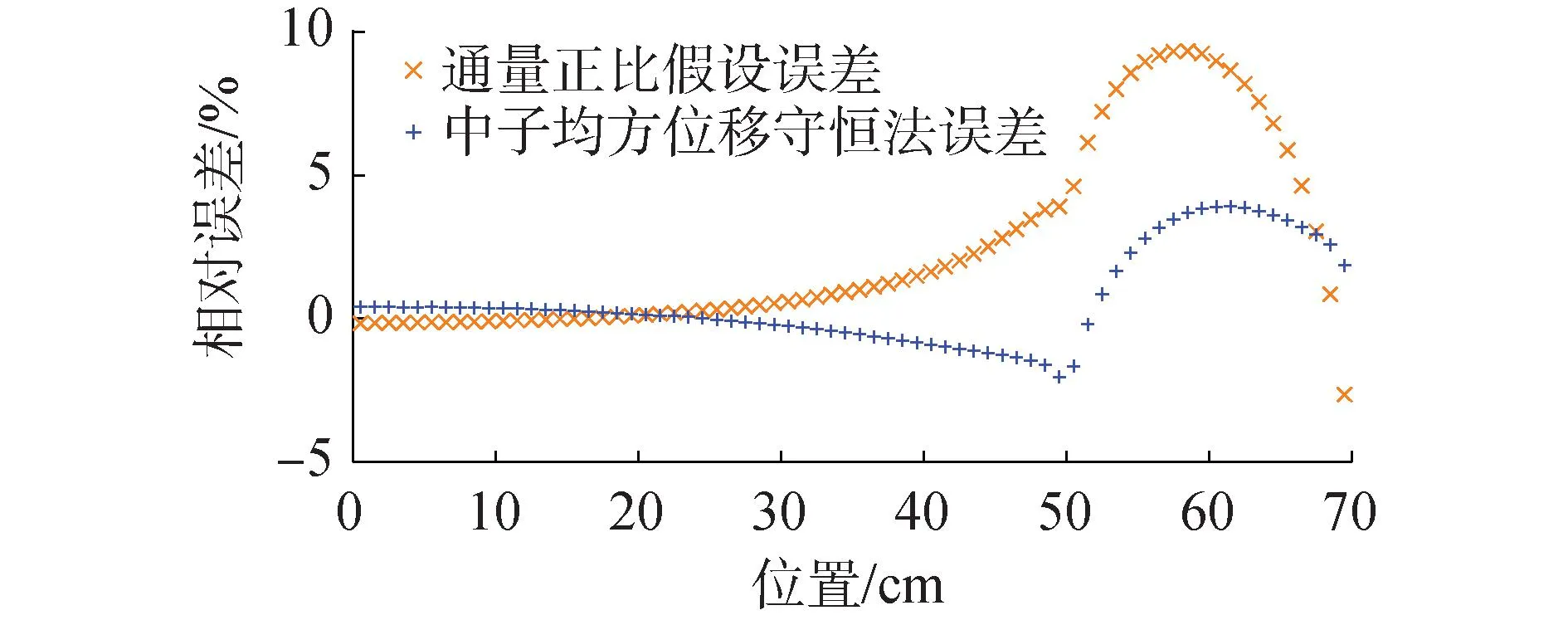
圖3 一維問題中子通量相對偏差分布Fig.3 Distribution of relative biases of neutron flux in one-dimensional problem

2.2 二維均勻堆芯問題

基于文獻[9]中的二維均勻堆芯問題對本文方法進行測試,為簡化問題,對燃料和反射層組件進行了打混,其核素組成與2.1小節相同。圖4中給出了本問題的堆芯布置,堆芯由5圈燃料組件和2圈反射層組件組成,其中組件對邊距為16.3 cm。

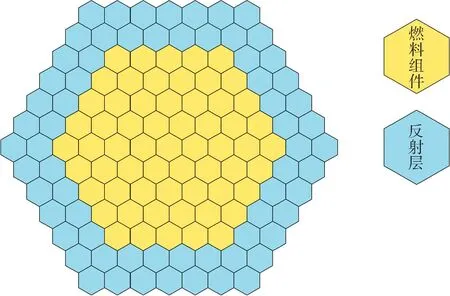
圖4 二維均勻堆芯問題布置圖Fig.4 Layout of two-dimensional homogeneous core problem

本文使用NECP-MCX連續能量模式計算參考解,并在求解過程中分別統計各位置處燃料組件和反射層組件的33群均勻化群常數,其中一階散射截面基于通量正比假設得到。計算時共投入1 300代,其中前300代為非活躍代,每代投入50萬個粒子。然后,使用中子均方位移守恒法分別計算了燃料和反射層的平均散射角余弦及修正因子,并對一階自散射截面進行修正。最后,分別使用修正和未修正的一階散射截面對該問題進行NECP-MCX多群計算。

表3中給出了本問題的keff計算結果,參考解為1.089 78±0.000 07。可以看出,使用修正截面可以將keff的偏差由0.007 96降低為-0.000 31。

表3 二維均勻堆芯問題有效增殖因子計算結果

圖5中給出了NECP-MCX計算得到的相對裂變反應率分布。圖6和圖7中分別給出了使用通量正比假設和修正截面計算得到的堆芯裂變反應率相對偏差分布。可以看出,使用修正截面后,最大相對偏差由3.754%下降到-0.990%,相對均方根偏差由1.864%下降到0.612%。

圖5 二維均勻堆芯相對裂變反應率分布Fig.5 Distribution of relative fission reaction rates in two-dimensional homogeneous core

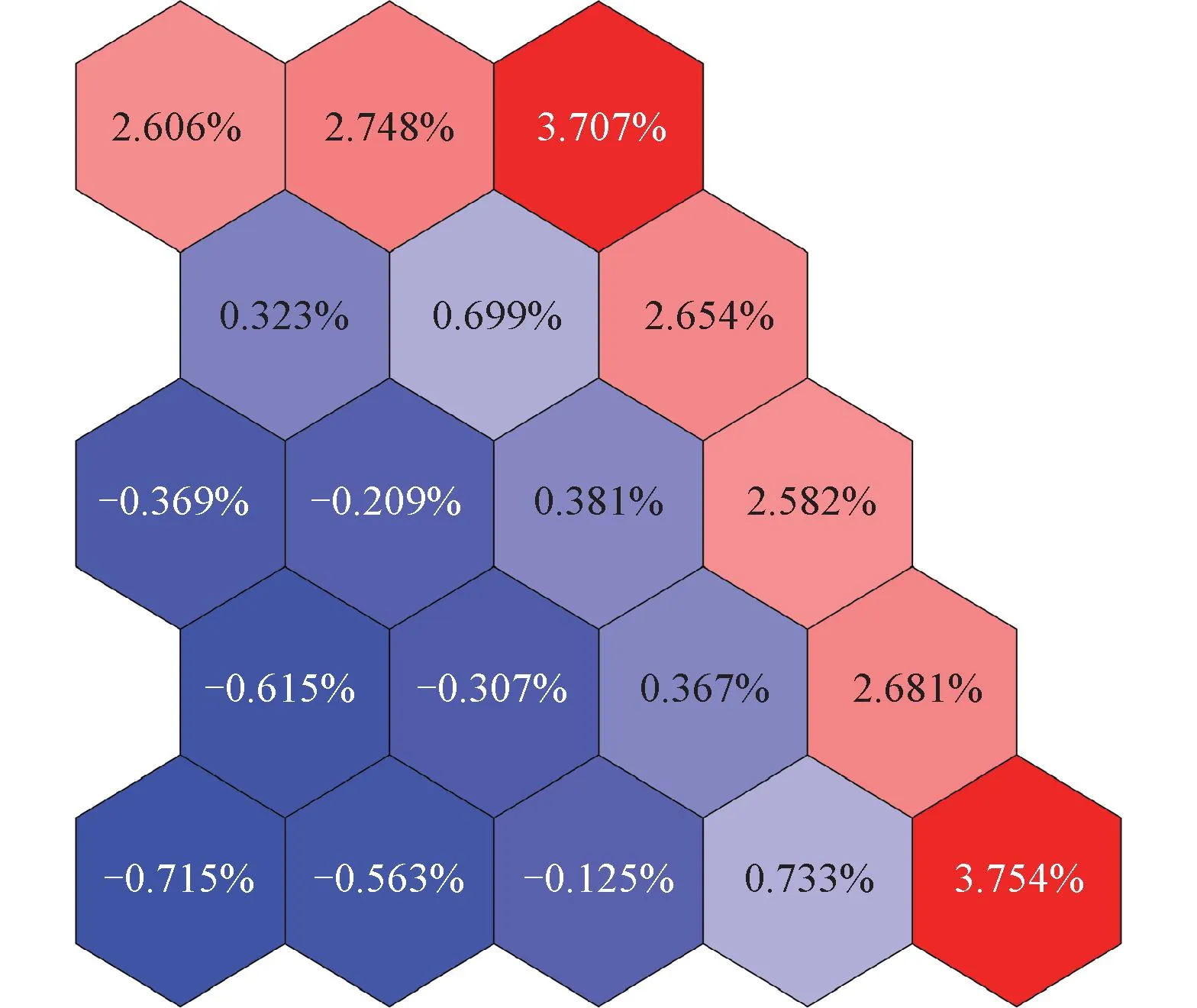
圖6 使用通量正比假設計算的二維均勻堆芯裂變反應率相對偏差分布Fig.6 Distribution of relative biases of fission reaction rates in two-dimensional homogeneous core calculated by using proportional flux assumption

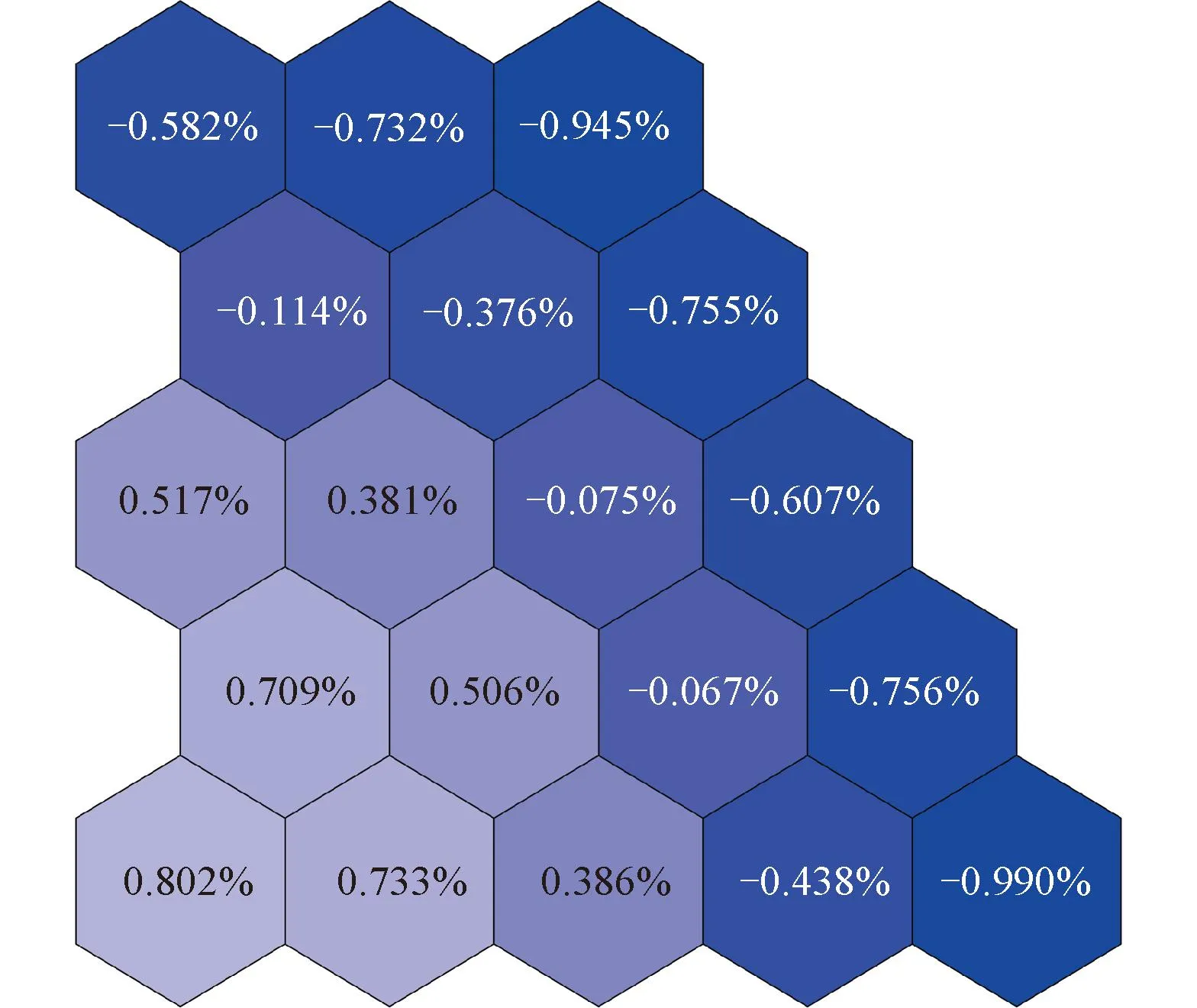
圖7 使用修正截面計算的二維均勻堆芯裂變反應率相對偏差分布Fig.7 Distribution of relative biases of fission reaction rates in two-dimensional homogeneous core calculated by using corrected cross-sections

2.3 二維非均勻堆芯問題

基于經合組織核能署(OECD/NEA)發布的鈉冷快堆基準題MET-1000問題[14],本文設計了二維非均勻堆芯問題。MET-1000為中等尺寸堆芯,堆芯內裝載金屬燃料,組件對邊距為16.247 cm。為簡化問題,各類型組件使用均勻模型,組件內不同材料核素組成及體積份額見文獻[14]。堆芯布置見圖8,堆芯內插入控制棒,增加了系統的各向異性。

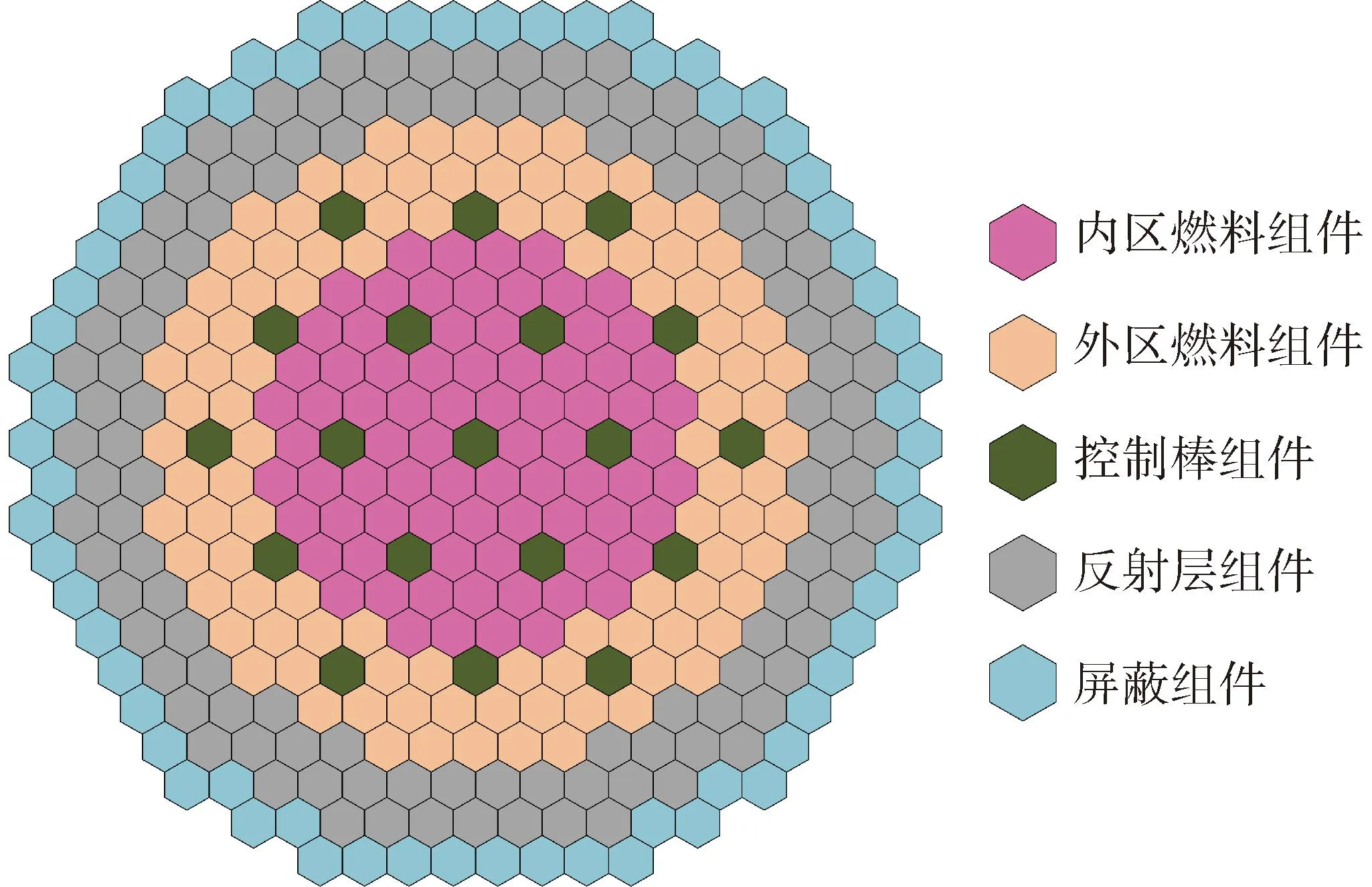
圖8 二維非均勻堆芯問題布置圖Fig.8 Layout of two-dimensional heterogeneous core problem

類似地,首先使用NECP-MCX連續能量模式計算參考解,并在求解過程中分別統計各位置處組件的24群均勻化群常數(能群結構見表4),其中一階散射截面基于通量正比假設得到。計算時共投入1 300代,其中前300代為非活躍代,每代投入100萬個粒子。然后,使用中子均方位移守恒法分別計算了5種組件的平均散射角余弦及修正因子,并對一階自散射截面進行修正。最后,分別使用修正和未修正的一階散射截面對該問題進行NECP-MCX多群計算。

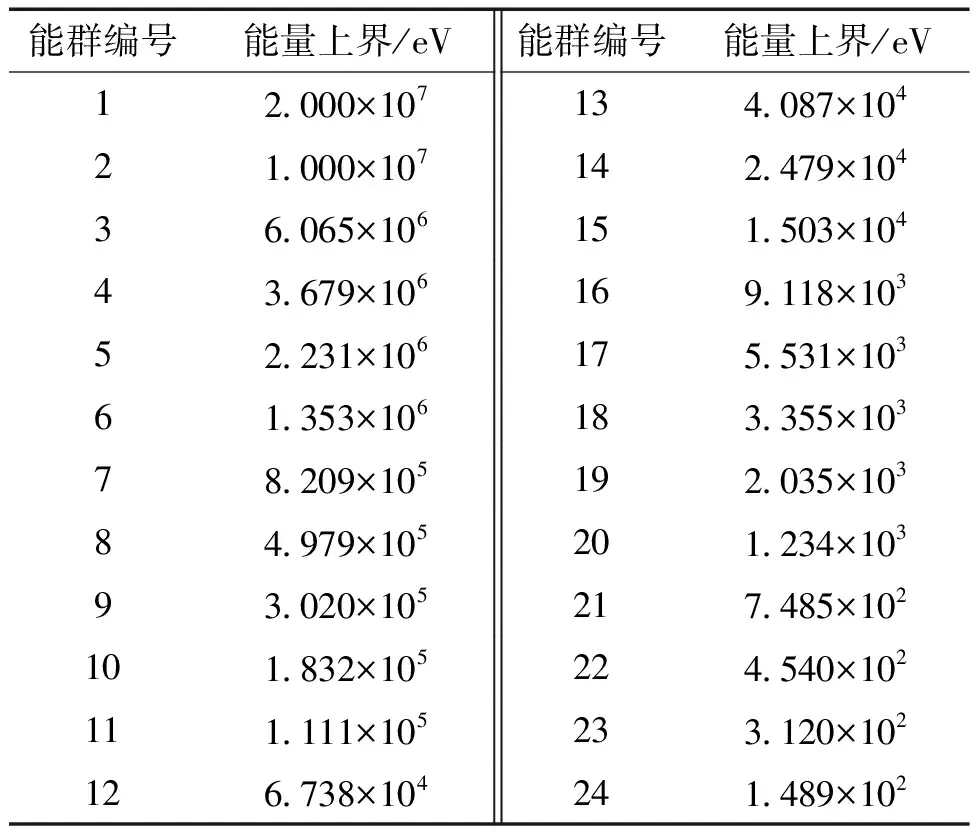
表4 24群能群結構Table 4 Structure of 24-group

表5中給出了本問題的keff計算結果,參考解為0.950 61±0.000 04。可以看出,使用修正截面可以將keff的偏差由0.007 17降低為0.002 66。

表5 二維非均勻堆芯問題有效增殖因子計算結果

圖9中給出了NECP-MCX計算得到的相對裂變反應率分布。

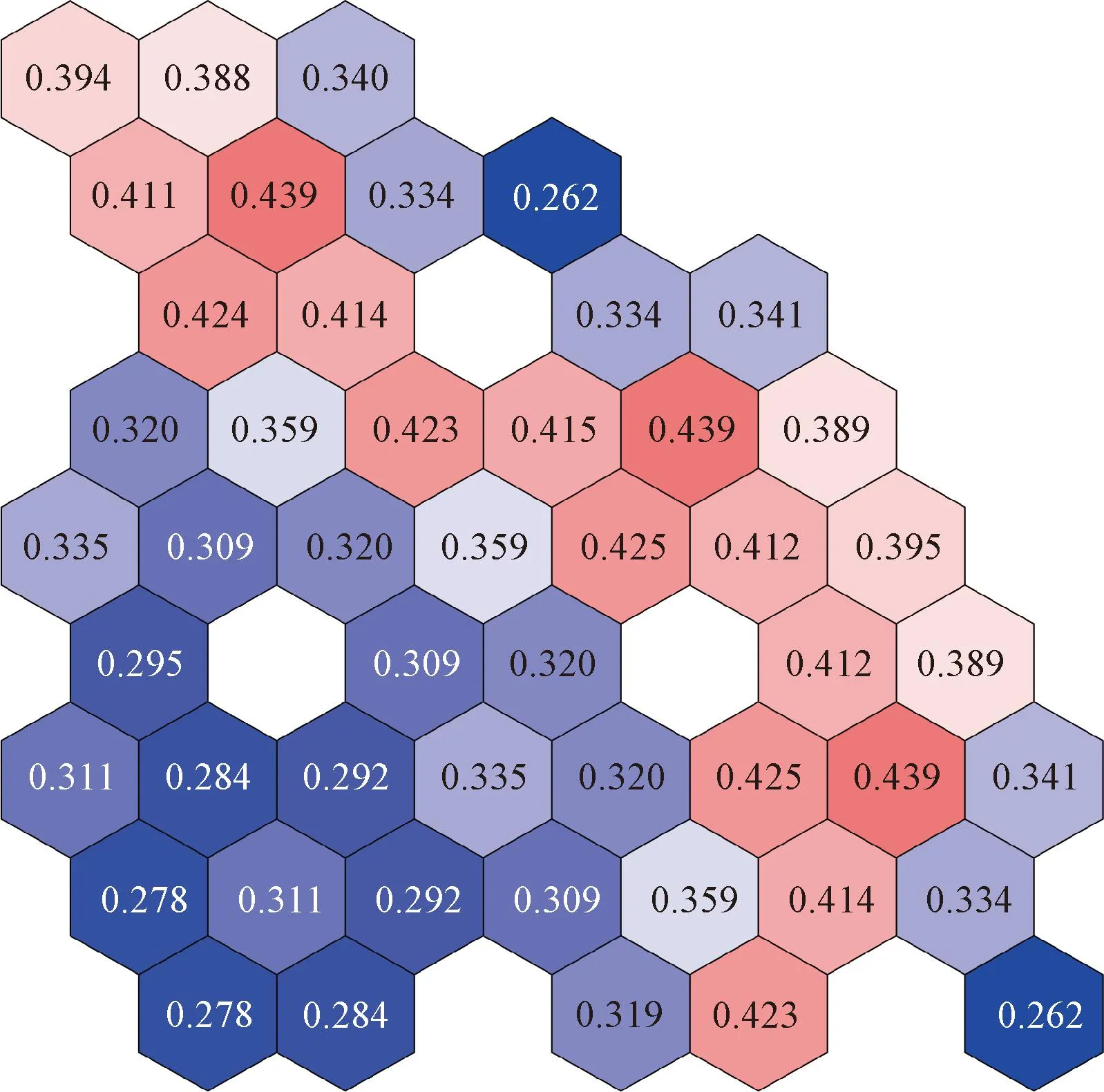
圖9 二維非均勻堆芯相對裂變反應率分布Fig.9 Distribution of relative fission reaction rates in two-dimensional heterogeneous core

圖10和圖11中分別給出了使用通量正比假設和修正截面計算得到的堆芯裂變反應率相對偏差分布。可以看出,使用修正截面后,最大相對偏差由4.675%下降到0.920%,相對均方根偏差由2.444%下降到0.569%。

圖10 使用通量正比假設計算的二維非均勻堆芯裂變反應率相對偏差分布Fig.10 Distribution of relative biases of fission reaction rates in two-dimensional heterogeneous core calculated by using proportional flux assumption

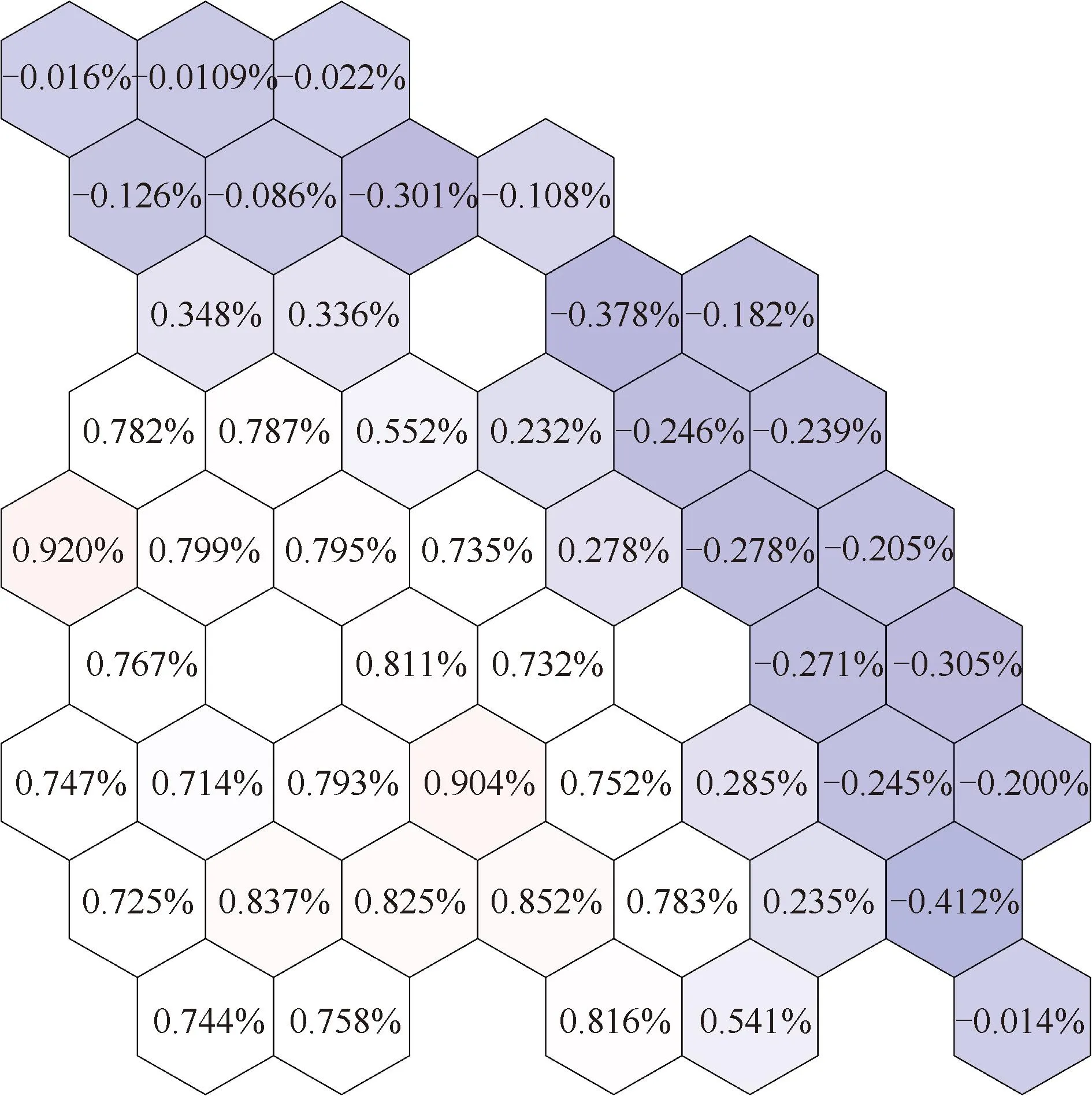
圖11 使用修正截面計算的二維非均勻堆芯裂變反應率相對偏差分布Fig.11 Distribution of relative biases of fission reaction rates in two-dimensional heterogeneous core calculated by using corrected cross-sections

2.4 擴散計算結果

本文對修正方法計算得到的高階散射矩陣進行數值測試,也對基于該方法產生的擴散系數進行數值測試。基于Inflow近似[3]和斐克定律,可得[8]:

(17)

式中:φg為中子通量;Σt,g為總截面;Dg為擴散系數。

當蒙特卡羅輸運計算結束后,式 (17)中除擴散系數外各項均已知,該式成為了關于擴散系數的線性方程組,求解該線性方程組即可得到擴散系數。分別使用通量正比假設方法和修正方法產生式 (17)中的一階散射矩陣,計算得到多群擴散系數,并基于該擴散系數對第2.3小節中的非均勻二維堆芯問題進行擴散計算,對基于本文方法產生的擴散系數進行數值測試。測試時計算條件設置與第2.3小節相同。

圖12和13為基于通量正比假設方法和修正方法的堆芯裂變反應率擴散計算相對偏差分布。

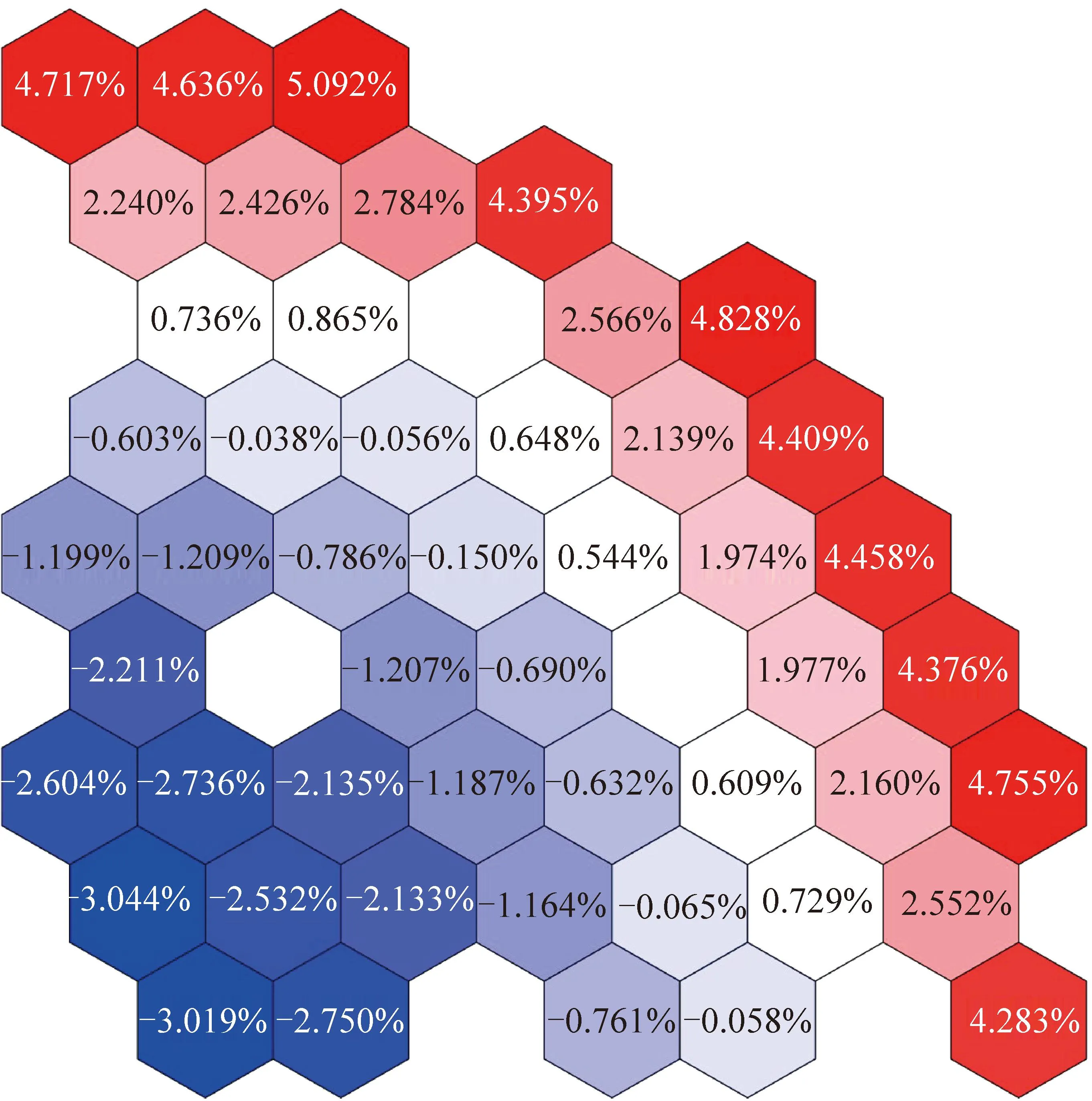
圖12 基于通量正比假設方法的堆芯裂變反應率擴散計算相對偏差分布Fig.12 Distribution of relative biases of fission reaction rates in core diffusion calculation based on proportional flux assumption

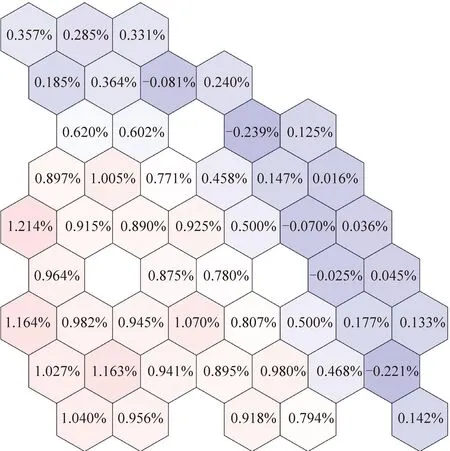
圖13 基于修正方法的堆芯裂變反應率擴散計算相對偏差分布Fig.13 Distribution of relative biases of fission reaction rates in core diffusion calculation based on correction method

可以看出,使用修正方法后,最大相對偏差由5.092%下降到1.214%,均方根偏差由2.609%下降到0.792%。可以看出,修正方法計算得到的擴散系數更為精確。

3 結論

本文提出的基于中子均方位移守恒的平均散射角余弦計算方法,算例對該方法進行了數值測試,驗證了本文的計算精度。與傳統方法相比,中子均方位移守恒法的計算精度更高,可以有效降低強各向異性問題的計算偏差。

本文僅對一階自散射截面進行了修正,下一步可對完整的高階散射矩陣修正展開研究。