找“周”測“長”?凸顯概念本質

黃海歐

【摘 要】“周長”是小學“圖形與幾何”領域的一個重要概念，對這一概念的不理解會影響后續有關實際問題的解決以及造成周長和面積概念的混淆。文章以“周長的認識”為切入點，著手研究幾何概念教學的改進模式，力求引導學生通過系列操作活動，經歷概念的發生、感知、形成和深化過程，把握“周長”的概念，發掘內在本質。

【關鍵詞】周長 概念本質 平面圖形

數學概念是數學知識的核心和數學思想方法的有效載體，正確理解和掌握概念是學生能力提升的保證?！爸荛L”是小學“圖形與幾何”領域的一個重要概念，它是平面圖形的本質屬性，是幾何知識的核心之一，也是培養學生空間意識的有效載體。然而，實際教學的成效卻往往不盡如人意，如在教學完周長概念后，學生在解決與周長有關的實際問題或是求不規則圖形的周長時感到困難；還有些學生到高年級后，將周長與后續學習的面積概念發生混淆等。這都是由于學生對周長表象建立不完善，對周長概念的理解不深、不透導致的，這也一直是幾何教學中的一個痛點。本文以“周長的認識”為切入點，著手研究幾何概念教學的改進模式，力求引導學生通過一系列操作活動，在經歷概念的發生、感知、形成和深化的過程中，把握“周長”的概念，發掘其內在本質。

一、教材分析，尋求本質點

人教版數學三年級上冊“周長”這一內容，是學生在學習了線段、長方形和正方形之后學習的，為今后學習多邊形的周長和圓的周長打下基礎。

筆者研讀了人教版、浙教版、西師大版、蘇教版、北師大版等教材，發現其內容都包含三個層面：首先是結合熟悉的實物或圖形去認識什么是周長；其次是掌握測量周長的方法；最后是應用周長概念解決問題。在這些版本的概念呈現環節中，人教版提供的素材是最多的，且只有人教版直接給出了周長的明確定義，從實物到圖形再到文字，實現了從具體到抽象的層層遞進。

二、學情分析，確定混淆點

為了進行學情分析，筆者設計前測題（如圖1）：

學生的前測數據如圖2：

可見，學生對“周長”的認知率是比較高的，但對本質概念的認識還存在一定的偏差。比如：部分學生根據已有線段測量的經驗，認為曲線圖形、不規則圖形用直尺不好測量，就沒有周長；學生在描一周時容易忽略周長的本質，把圖形內部的線條也看作周長的一部分。另外，由于周長和面積的表象都是借助封閉圖形表現出來的，學生對面積的感覺又遠比周長強烈，很容易將這兩者混淆，導致以“大小”來判斷周長的長短。所以，筆者將本節課的教學重點立足在準確把握“周長”的概念上，凸顯“周長”概念的本質。

三、實踐過程，落實關鍵點

【片段一】讓周長在“周”的基礎上生長

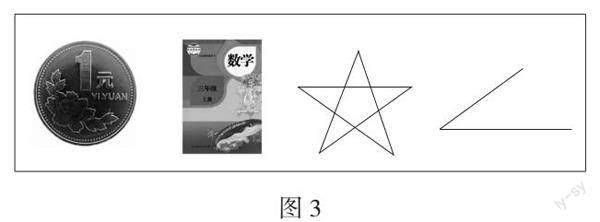
1.任務一：這些圖形有一周嗎？如果有，用水彩筆描出它一周的邊線。（如圖3）

2.匯報交流。

追問1：五角星里面為什么不描？

追問2：角呢？

小結：這是圓的一周、數學課本封面的一周、五角星的一周。角不是封閉圖形沒有一周。

3.變式。

問題：怎么變，它才會有一周，請描出來。（學習單上操作）

追問1：還可以怎么變？它們的一周在哪里？

追問2：只要怎么變，就會有一周？

小結：只有封閉圖形才有一周。

【設計意圖】在任務一的解決過程中，學生描出邊線后，同桌之間交流評價。讓學生學會從已有認知出發，自學教材內容，嘗試解決問題。所提供的素材有具體實物，也有抽象圖形，旨在用最精簡的素材，從行動表征到圖象表征，再到語言表征，幫助學生一步步建立起“一周”的表象，獲得鮮明形象的認識。重點辨析有內部線條的五角星和不封閉的角之后，讓學生想象角怎么變就會有一周，學生最先想到的是三角形，再針對前測中學生認為曲線圖形和不規則圖形沒有周長的學情，讓學生創作既有曲線又不規則的變式圖形，要求學生辨析是否有一周，得到“只要是封閉圖形就有一周”的結論。在培養學生空間想象力的同時，拓展了“周長”這一概念的外延，讓學生在不同外延中深刻感受“封閉邊線”的含義，為接下來的測量、計算打下了認知基礎。

【片段二】讓周長在“長”的基礎上延續

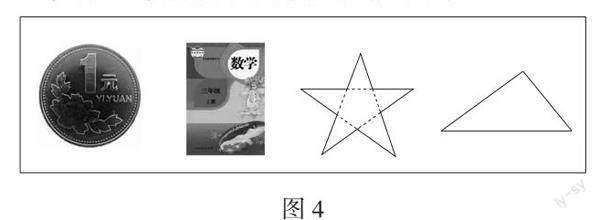
1.任務二：完成下面的填空。（如圖4）

我想測量的周長。

想一想：怎么測量。

選一選：我需要的工具是。

測一測：它的周長是厘米。（結果取整厘米）

2.匯報交流。

（1）三角形。

小結：測量了3次，這三條邊的長度和就是三角形的周長。

（2）長方形。

生1：測量了4次。

生2：測量了2次，長量1次，寬量1次就可以了。

小結：雖然生2測量了2次，但“×2”后，也是在求四條邊的長度和，這四條邊的長度和就是長方形的周長。

（3）五角星。

生1：把五角星的每一條邊都量了一遍，然后把所有的長度都加起來。

生2：只要量一條邊，再乘10就行。

小結：雖然生2測量了1次，但“×10”后，也是在求十條邊的長度和，就是五角星的周長。

（4）圓。

生1：用卷尺把它繞起來。

生2：用線把它繞一圈，再測量線的長度。

小結：不管是圍還是滾，都是數學上所講的“化曲為直”。求的是一圈的長度和，就是圓的周長。

演示總結：不管是圓的周長、三角形的周長、長方形的周長還是五角星的周長，都是一周的長度。（如圖5）

【設計意圖】認識了圖形的一周之后，學生自主完成任務二——測長。學生選擇自己想要測量的圖形，先思考如何測量，再選擇合適的工具進行測量，記錄過程，得出結論。從最簡單的三角形入手進行交流展示，由簡到繁，層層遞進；接著對比長方形的兩種測法，通過測量次數的減少，體現學生基于圖形直觀特征的算法優化；五角星的周長則幫助學生進一步感受“積段成數”；圓作為曲線圖形，它的測量更具有挑戰性。學生發現繞圓的繩子拉直后依舊能表示圓的周長，是因為長度沒有發生變化，“化曲為直”的數學思想得到自然滲透。在學生深刻體驗的基礎上，教師進行動畫演示，進一步讓學生感悟無論“一周”的形怎樣變化，周長都是邊線長度的總和，在形與線段的變換中逐步領悟周長的內涵，積累數學學習活動經驗，培養空間觀念。

【片段三】讓周長在操作中深刻

1.任務三：你能把這個長方形分成周長相等的兩部分嗎？（如圖6）

2.匯報交流。

問題：為什么這兩部分的周長相等？（如圖7）

3.任務四：剪掉一塊，剩下圖形的周長和原來長方形的周長相比，有什么變化？（如圖8）

4.追問：剪掉一塊，剩下圖形的周長不變，還有其他情況嗎？

【設計意圖】學生能否靈活應用概念，最合適的檢測方法就是在變化中思辨。因此，筆者設計了兩個習題。第一題基于形與量的思考，形狀上，從均分變為大小不一；數量上，從單個圖形到一分為二。這樣的思辨不僅是對周長理解的深入，還在一定程度上促使學生打破思維定式，排除面積的視覺干擾，重新回到“周長”概念的內涵上進行對比辨析。第二題旨在關注解決問題方法的多樣性與層次性。之前，學生求周長的方法只有量，這時可以利用所學知識進行抽象和推理，提升思維層次。筆者適時追問，要求學生進行思考，感受周長的三種變化情況——不變、變長、變短，在“變”與“不變”中，深入發掘周長的本質。

四、課后反思，呵護生長點

數學課的學習要解學生之困，那這節概念課，學生之困“困”在何處呢？

（一）周長在哪里

首先，學生的困難在于不會準確找到“周長在哪里”。所以，筆者在任務一中提供了“角”這樣的學習素材，先提問：“角怎么變，也有一周？”并不斷追問：“還可以怎么變？”通過這樣的變化，學生經歷多個層次的想象，先是基于經驗的想象連接出三角形，之后突破經驗的想象，得到多邊形和有曲線的不規則圖形的周長。這時，筆者繼續追問：“只要怎么樣都有一周？”通過問題引導學生總結。由此，學生對“一周”的理解真正得到了修正和內化。

（二）周長怎么測

其次，學生困在“周長怎么測”。在測量周長環節，筆者給學生提供了豐富的素材，如三角形、長方形、五角星等都可以通過測量直接得出周長，圓的周長則需要通過轉化再測量。得出數據之后，筆者不滿足于此，引導學生歸納提煉“不管怎么測、測幾次，都是求這個圖形一周的長度”，讓學生深刻體會“積段成數”“化曲為直”的方法。

（三）周長怎么比

我們知道，面積與周長是共存的，顯性的面積一直影響著隱性的周長。筆者沿用任務二中長方形這一素材，設置了任務三：“你能把這個長方形分成周長相等的兩部分嗎？”這一任務靈活多變，適合不同發展層次的學生。課堂上，思維層次低的學生，只能通過把長方形分成兩個形狀大小相同的圖形，借形判斷周長相同，而思維層次高的學生可以脫離形，通過推理從概念本質上去判斷，提升了靈活解決問題的能力，同時為后續周長和面積的辨析做好鋪墊。

總之，概念課的教學要基于學生的自主構建，關注概念本質，在思辨中發展學生思維。本節課，筆者引導學生通過一系列操作活動，在經歷概念的發生、感知、形成和深化的過程中，找“周”測“長”，凸顯了概念的本質，讓學生的深度學習真正發生。學生由此獲得的不僅是知識技能，更重要的是抽象思維、推理思維層次的提升。