基于狀態空間模型的加工中心功能銑頭實時壽命預測

劉麗娜，秦飛躍，2，宋欣鋼

(1.黃河交通學院機電工程學院，河南焦作 454950；2.河南理工大學機械與動力工程學院，河南焦作 454003)

0 前言

數控機床是目前最為熱門的加工設備，而銑頭是數控機床中最重要的設備之一。銑頭加工成本較高、生產周期較長，因此在有限的環境和運行數據下，建立銑頭的壽命預測模型具有重要的研究意義[1]。銑頭在運行過程中因關鍵零部件磨損、結構問題以及本身質量問題，導致加工精度下降，進而使得銑頭失效[2-3]。當銑頭出現一定的磨損之后，最直接的表現就是溫度不斷上升，因此可以通過測定運行過程中的溫升數據判斷銑頭的運行狀態[4]。彭衛文等[5]使用運行過程中的溫升數據，應用貝葉斯方法，結合故障機制構建加速性能退化實驗，建立了銑頭的可靠性評估預測模型。劉毅[6]分析了直角銑頭的常見故障，發現直角銑頭故障一般都是由臺階、螺旋傘齒輪齒面以及軸承磨損、殼體破壞等構成，故障的主要原因還是銑頭內部磨損。但是，目前有關銑頭的壽命預測模型研究相對較少，再者銑頭的壽命預測數據相對難以獲取，許多研究學者目前主要采用可靠性研究方法對數控機床及其關鍵零部件進行壽命預測[7-8]。

銑頭運行過程中的溫度升高是其內部磨損、性能退化的直接體現。實際生產過程中，銑頭的退化狀態不可直接測量，本文作者提出基于狀態空間模型對銑頭運行過程中的退化狀態進行描述，并使用貝葉斯狀態估計對建立的模型進行求解，計算銑頭的失效時間分布，實現對銑頭實時壽命的預測[9]。

1 模型建立

在設備或者系統運行過程中，會呈現出兩種狀態變量：一種是可以直接通過相應的傳感器測量到的數據，這種狀態變量稱為觀測量，也可稱為可觀測序列；另外一種是無法通過相應的傳感器測量，但是卻真實存在的變量，這種狀態變量稱為狀態向量。狀態向量能真實反映出設備或者系統運行的內在運行狀態，它由一個馬爾科夫鏈構成。狀態空間模型建立了可觀測量與狀態向量之間的關系，通過狀態空間模型，能將設備或者系統運行過程中的內在狀態呈現出來。

圖1描述了系統或者設備運行過程中可觀測量與狀態向量之間的關系，其中A0，A1，…，An，An+1指的是系統或者設備運行過程中的狀態向量，與之對應的B0，B1，…，Bn，Bn+1是系統或者設備的可觀測序列。

圖1 狀態向量與可觀測序列之間的關系Fig.1 Relationship between state vector and observable sequence

貝葉斯狀態估計與預測可以用來對狀態空間模型求解。每當傳感器觀測到一個數據時，可以得到一個先驗分布，通過貝葉斯公式計算得到一個后驗分布。當觀測到新數據時，之前產生的后驗分布可以作為先驗分布，繼續參與計算得到新的后驗分布，如此循環往復，每當觀測到新的數據，就可以及時更新模型參數，從而實現對設備或者系統的狀態估計。

銑頭作為一種復雜的精密機械設備，隨著運行時間的增加，會因為關鍵零部件磨損而使得加工精度降低，而關鍵的零部件磨損無法通過相應的傳感器測量出來，最終表現出來的是銑頭溫度增加，因此可以通過測量溫度，利用建立的狀態空間模型實現對銑頭的壽命預測。

銑頭性能退化及實時壽命的狀態空間模型可以通過式(1)來實現[10]：

(1)

其中：gθ(·)為狀態方程，描述銑頭退化狀態隨著運行時間的變化關系；fθ(·)為觀測方程，指銑頭在運行過程中溫度與其內部的關系；t為銑頭的運行時間；yt為銑頭運行到t時刻的可觀測序列，即溫度；xt為銑頭運行到t時刻的實際退化狀態；wt和vt分別為系統的過程噪聲和觀測噪聲。

已知t時刻的銑頭狀態后驗分布π(xt|y1，t)，根據貝葉斯公式，可得到任意t+k的狀態分布：

π(xt+k|y1,n)=

(2)

累積失效概率指設備或者系統運行期間內的失效概率。假設文中研究對象銑頭設定的溫度閾值為TR，當銑頭運行過程中溫度Tr超過設定的閾值時，即可判定銑頭失效。設F(t)為銑頭運行t時刻后的累積失效概率，累積失效概率計算公式[11]為

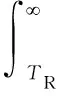
(3)

利用式(2)得到t+k時刻的狀態分布后，根據式(3)可以得到t+k時刻的銑頭累積失效概率為

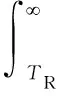
(4)

失效概率密度是對累積失效概率公式的微分，銑頭在t時刻的失效概率密度的表達式為

本次研究納入的4100例孕婦中共計有26例經產后或者引產證實為胎兒肢體缺陷。產前常規超聲檢出12例，聯合檢查檢出17例，連續順序追蹤超聲檢出25例。連續順序追蹤超聲檢出效果明顯優于其他超聲檢查，P＜0.05，差異具有統計學意義，見表1。

(5)

給定銑頭的溫度后，以動態線性增長模型作為狀態方程，描述銑頭的退化軌跡[12]，如式(6)所示：

(6)

使用R語言對建立的銑頭性能退化模型進行編程并求解[13]，可以得到任意時刻陶瓷銑頭的性能退化狀態、累積失效概率以及失效概率密度。

任何預測模型得出的結果與真實值都有一定的偏差，在預測過程中也有一定的不確定性，為了消除此種不確定性帶來的影響，在預測模型中引入置信區間來增加預測結果的可靠性，文中將置信區間設置為95%。

2 結果與分析

2.1 銑頭退化狀態估計與預測

由于壽命數據具有難以獲取、樣本小以及成本高等特點，因此文中使用的銑頭在運行過程中的溫度數據及其獲取方法見文獻[5]。圖2所示為銑頭運行過程中的溫升數據。

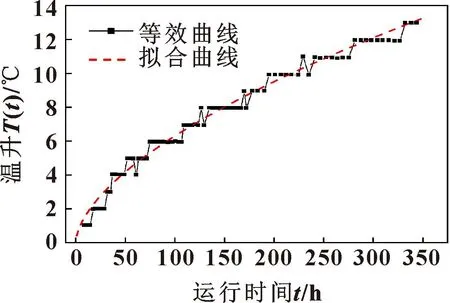
圖2 銑頭溫升數據Fig.2 Milling head temperature rise data

通過對銑頭溫升的數據進行最小二乘擬合，可以得到銑頭壽命公式如式(7)所示：

T(t)=0.408 8×t0.593 9

(7)

其中：t為銑頭實際運行時間，h；T(t)為銑頭溫升，℃。

假設當溫升達到13 ℃時，銑頭壽命結束。通過式(7)計算此時銑頭理論運行時間為338.6 h。

圖3所示為基于銑頭運行前110 h的溫升數據得到的銑頭預測運行時間。通過上述建立的狀態空間模型計算出銑頭溫升為13 ℃時所需要的運行時間為191.8 h，與通過式(7)計算出的理論運行時間338.6 h差別較大。銑頭運行前110 h時退化狀態變化率δ110=0.023。圖中陰影面積為根據式(3)(4)、使用前110 h的溫升數據計算得到的運行第220 h時銑頭的累積失效概率。此時的陰影面積較小，說明銑頭在較短的運行時間時，失效概率較低，銑頭可靠度較高。

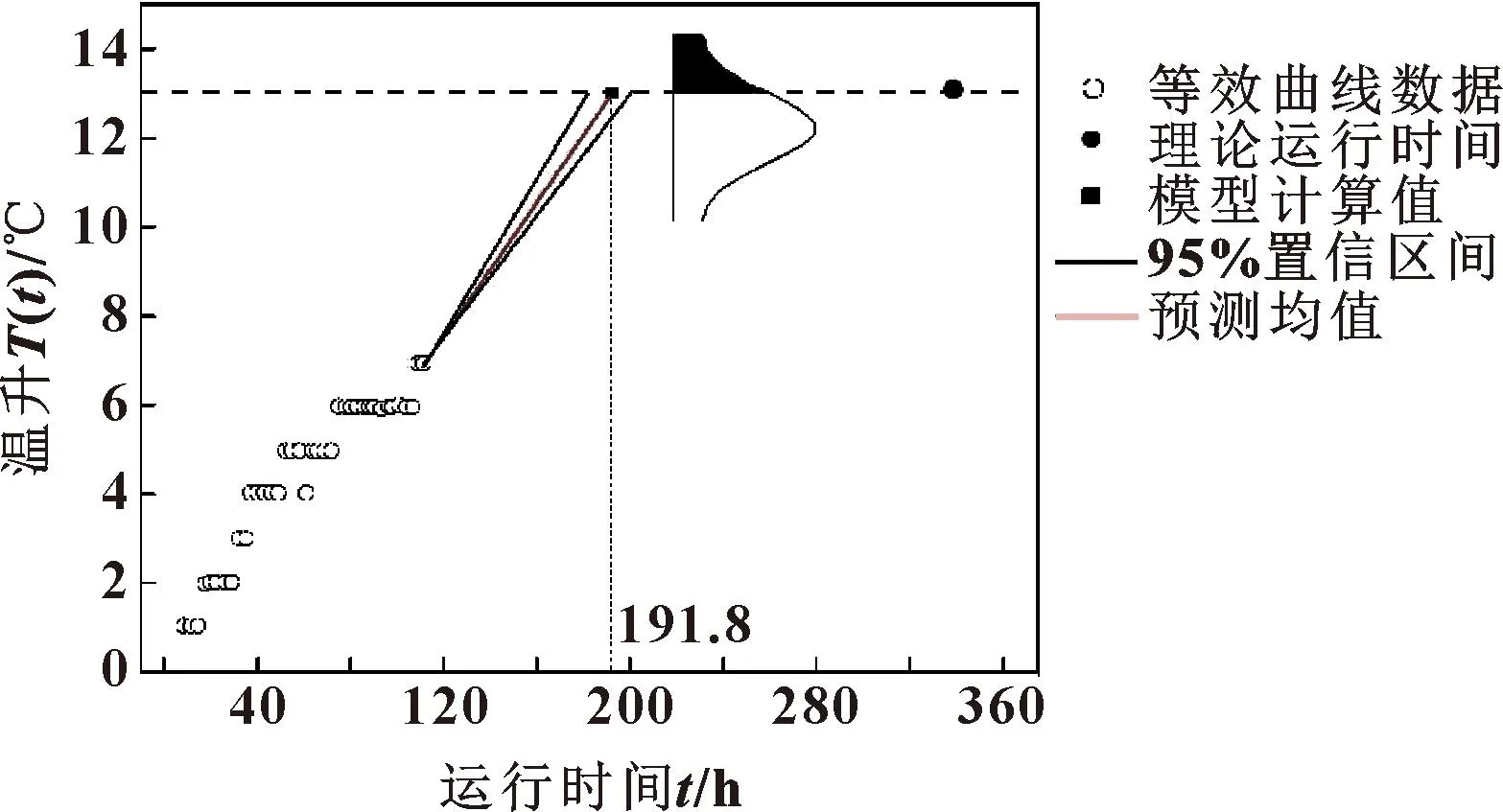
圖3 基于運行前110 h銑頭溫升數據的退化狀態估計與預測Fig.3 Degradation state estimation and prediction based on the first 110 h milling head temperature rise data

圖4所示為基于銑頭運行前220 h的溫升數據得到的銑頭預測運行時間。通過狀態空間模型計算出銑頭溫升為13 ℃時所需要的運行時間為275.3 h，與通過式(7)計算出的理論運行時間338.6 h還是有一定的差別，但是與運行前110 h溫升數據相比，差別進一步縮小。銑頭運行前220 h時退化狀態變化率δ110=0.015，退化狀態變化率與運行前110 h相比，進一步減小。圖中陰影面積為根據式(3)(4)、使用前220 h的溫升數據計算得到的運行第310 h時銑頭的累積失效概率。此時與前110 h溫升數據對比，陰影面積增大，說明銑頭在又運行了110 h后，失效概率增大，可靠度降低。

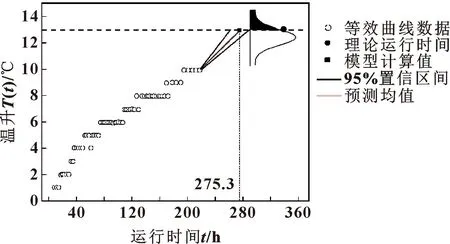
圖4 基于運行前220 h銑頭溫升數據的退化狀態估計與預測Fig.4 Degradation state estimation and prediction based on the first 220 h milling head temperature rise data

圖5所示為基于銑頭運行前310 h的溫升數據得到的銑頭預測運行時間。通過狀態空間模型計算出銑頭溫升為13 ℃時所需要的運行時間為330.5 h，與式(7)計算出的理論運行時間338.6 h差別進一步縮小。可以看出：在置信區間內，失效時間預測已經超過理論運行時間，證明預測模型的準確性。由于失效時間預測已經超過理論運行時間，因此再對運行338.6 h后銑頭的累積失效概率計算已經沒有實際意義，這里不再給出累積失效概率預測圖。銑頭運行前310 h時退化狀態變化率δ110=0.008，其退化狀態變化率進一步減小，這也能與圖2銑頭溫升數據前期增加較快、后期增加較慢相印證。

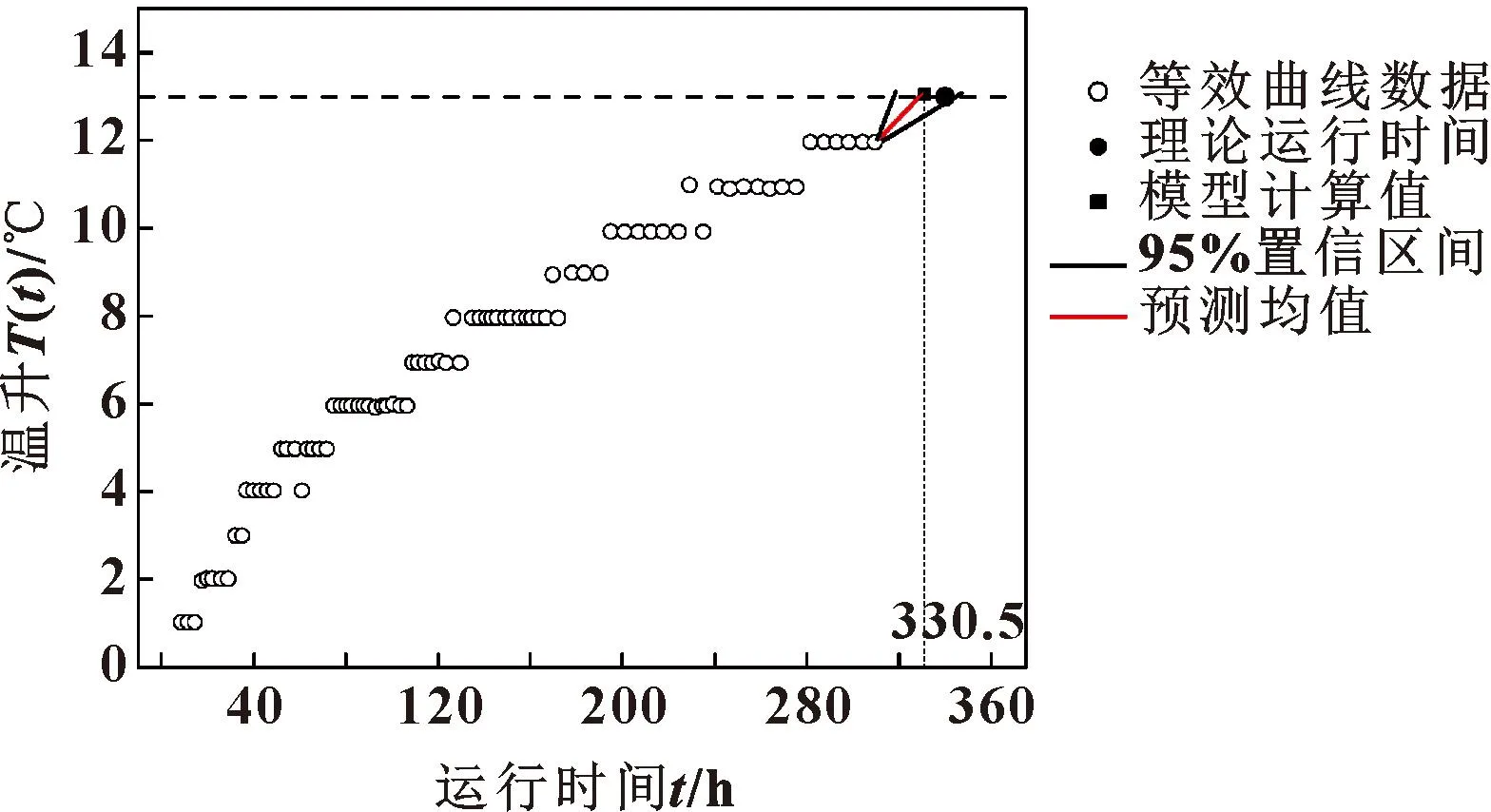
圖5 基于運行前310 h銑頭溫升數據的退化狀態估計與預測Fig.5 Degradation state estimation and prediction based on the first 310 h milling head temperature rise data

2.2 銑頭失效概率密度預測

結合式(4)(5)計算可以得到任意時刻銑頭的失效概率密度分布。文中分別選取銑頭運行前110、220、310 h時的溫升數據，計算對應的失效概率密度分布，如圖6所示。其中豎直垂線是銑頭溫升閾值為13 ℃時，由式(7)計算得到的理論運行時間，為338.6 h。

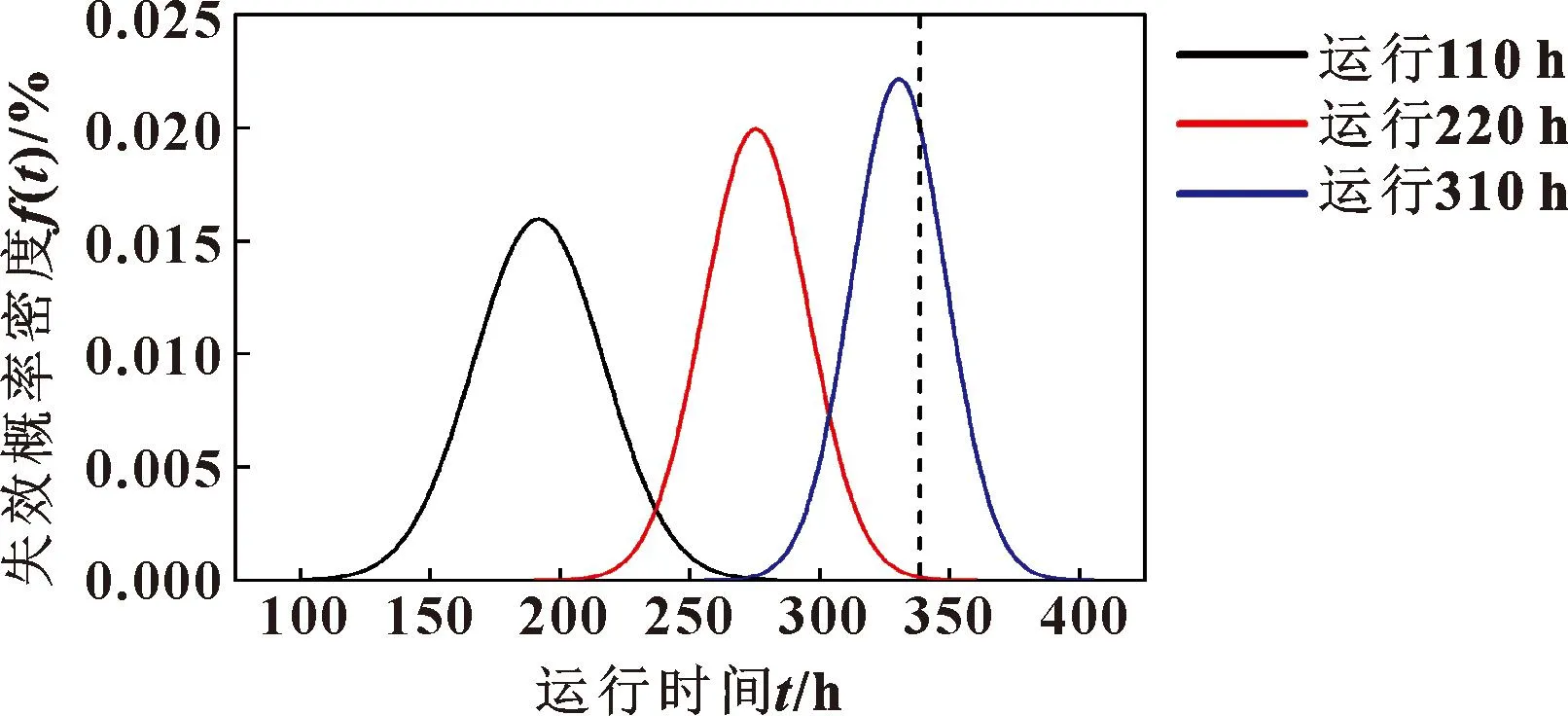
圖6 銑頭失效概率密度預測Fig.6 Failure-probability density prediction of milling head

由圖6可以看出：隨著溫升數據不斷增多，銑頭失效時間預測越來越收斂于理論值，說明模型預測的不確定性越來越小。這是因為貝葉斯能不斷融入新的溫升數據，通過計算先驗分布和后驗分布來及時更新狀態空間模型參數。

3 結論

銑頭在運行過程中，由于關鍵零部件磨損使得加工精度降低，從而導致其性能狀態不斷退化，而且退化狀態不可直接測量，只能通過測定運行過程中銑頭溫升來判斷退化狀態；同時銑頭壽命數據具有難獲取、樣本小以及成本高等特點，使得難以實時預測銑頭壽命。文中以實際運行過程中銑頭溫升數據為基礎，結合狀態空間模型與貝葉斯理論，建立了銑頭的實時壽命預測模型。得到的結論如下：

(1)建立的銑頭實時壽命預測模型可以根據前期銑頭的溫升數據，來預測任意時刻銑頭退化狀態以及剩余壽命，并且可以根據最新融合的溫升數據及時更新模型參數，從而使得預測結果越來越收斂于理論值。

(2)隨著運行時間的增加，預測模型計算得到的銑頭退化狀態變化率逐漸減小，這與銑頭剛開始投入使用時溫升增加較快、后期增加較慢這一現象相互印證。

(3)不同運行時間內，模型計算出的銑頭失效概率密度隨運行時間的增加不斷接近真實值，一定程度上可以為銑頭失效做出判斷。