聚焦知識(shí)的生長(zhǎng) 體驗(yàn)高效的教學(xué)*
——以一節(jié)公開(kāi)課為例

廣州市番禺區(qū)教師進(jìn)修學(xué)校(番禺區(qū)教師發(fā)展中心)(511488) 郭施敏

在“雙減”政策下,如何在課堂切實(shí)做到“減負(fù)增效”是目前一線教師亟需解決的難題. 因此廣東省基礎(chǔ)教育初中數(shù)學(xué)科教研基地(廣州市)舉辦了一次“堂上高效率,課外輕負(fù)擔(dān)”的研討活動(dòng). 在此活動(dòng)上筆者進(jìn)行了“去分母法解一元一次方程”的課例展示,并收到了同行的一致好評(píng).

高效課堂體現(xiàn)在教師高效的教與學(xué)生高效的學(xué),其中要求教師具備重要的教學(xué)觀是“以生為本”,教師需重點(diǎn)關(guān)注學(xué)生數(shù)學(xué)知識(shí)的生成過(guò)程,同時(shí)也是數(shù)學(xué)知識(shí)的生與長(zhǎng)的過(guò)程.聚焦知識(shí)的生與長(zhǎng),其實(shí)是從本質(zhì)上解決學(xué)生在學(xué)習(xí)新知識(shí)過(guò)程中對(duì)數(shù)學(xué)知識(shí)理解的錯(cuò)覺(jué)和偏差. 對(duì)于數(shù)學(xué)的一些知識(shí),不少教師為了凸顯程序化操作,把解法歸納為具體的操作步驟,突出了此類解法的程序化. 接受這樣教學(xué)的學(xué)生往往對(duì)數(shù)學(xué)知識(shí)的理解停留在知其然而不知其所以然,他們對(duì)數(shù)學(xué)知識(shí)的認(rèn)識(shí)是機(jī)械的、片面的,不利于其后續(xù)發(fā)展和解決真實(shí)世界的數(shù)學(xué)問(wèn)題.

基于上述的背景, 本文將基于知識(shí)發(fā)生和發(fā)展的視角,以“去分母法解一元一次方程”的教學(xué)為例,嘗試對(duì)初中數(shù)學(xué)高效教與學(xué)進(jìn)行探索,以期獲得一些啟發(fā).

1 聚焦知識(shí)的發(fā)生

1.1 分析學(xué)生認(rèn)知的起點(diǎn)

去分母法解一元一次方程是人教版七年級(jí)上冊(cè)第三章第三節(jié)的內(nèi)容,“去分母”解一元一次方程是運(yùn)用等式的基本性質(zhì)解含分?jǐn)?shù)系數(shù)的一元一次方程,它是“去括號(hào)、移項(xiàng)、合并同類項(xiàng)、系數(shù)化為1”解一元一次方程的繼續(xù),本節(jié)學(xué)習(xí)內(nèi)容蘊(yùn)含轉(zhuǎn)化與化歸的數(shù)學(xué)思想,是解方程的核心. 解方程的核心是“復(fù)雜化簡(jiǎn)單,簡(jiǎn)單到‘x=a’;多元化少元,少到一元;高次化低次,低到一次”. 本節(jié)課為后續(xù)建立方程模型解決實(shí)際問(wèn)題、二元一次方程組、不等式、一元二次方程等內(nèi)容奠定了知識(shí)與思想方法基礎(chǔ).

七年級(jí)學(xué)生對(duì)本課的內(nèi)容已有一定的認(rèn)知基礎(chǔ),如已掌握有理數(shù)乘法分配律,已積累分?jǐn)?shù)可化為整數(shù)的經(jīng)驗(yàn),能運(yùn)用等式的性質(zhì)解簡(jiǎn)單方程,具備一定的分析問(wèn)題和轉(zhuǎn)化問(wèn)題的能力. 但是他們對(duì)本課內(nèi)容也有一定的認(rèn)知障礙,如去分母的提出與認(rèn)同可能產(chǎn)生一定的障礙,對(duì)等式性質(zhì)2 的理解水平一般,常常會(huì)出現(xiàn)理解偏差,同時(shí)在解方程中化歸思想方法儲(chǔ)備不足.

問(wèn)題1什么是解方程?

學(xué)生活動(dòng)根據(jù)之前所學(xué)知識(shí),學(xué)生快速回答.

教師活動(dòng)教師對(duì)學(xué)生回答進(jìn)行提煉也是開(kāi)篇的點(diǎn)睛之筆,萬(wàn)千世界林林總總的方程,最終化為“x=a”的形式,體會(huì)“追求簡(jiǎn)單化”的數(shù)學(xué)靈魂.

問(wèn)題1 開(kāi)門見(jiàn)山,既明確解方程的目標(biāo),又滲透化歸的數(shù)學(xué)思想,讓學(xué)生體會(huì)數(shù)學(xué)追求簡(jiǎn)單化.

1.2 研究知識(shí)的承接

基于對(duì)學(xué)生認(rèn)知的分析和對(duì)七年級(jí)教材的研究,不難發(fā)現(xiàn)學(xué)生不學(xué)習(xí)“去分母”也是能夠解決一元一次方程的問(wèn)題,因此本課首先要解決的是學(xué)生對(duì)于本課內(nèi)容學(xué)習(xí)的必要性解釋,也就是“為什么要學(xué)習(xí)‘去分母’解一元一次方程”.

研讀七年級(jí)上冊(cè), 發(fā)現(xiàn)在第一單元如圖1(即課本第33頁(yè))陳述有理數(shù)的分配律時(shí),課本選用了例題4 雙法對(duì)照說(shuō)明分配律的優(yōu)勢(shì),并在此后提出了思考. 思考題中提到哪種解法運(yùn)算量小. 事實(shí)上已經(jīng)解答了學(xué)生“為什么要學(xué)習(xí)‘去分母’解一元一次方程”. 去分母的核心是把分?jǐn)?shù)系數(shù)方程轉(zhuǎn)化為整數(shù)系數(shù)方程,從而運(yùn)算量更小. 根據(jù)以上分析,設(shè)計(jì)了教學(xué)環(huán)節(jié)的第二個(gè)問(wèn)題,具體如下:

圖1 人教版七年級(jí)上冊(cè)第33 頁(yè)

問(wèn)題2解方程.

學(xué)生活動(dòng)學(xué)生分小組討論,得到兩種解法,大部分學(xué)生快速得到移項(xiàng)的解法,少數(shù)可以考慮到去分母的解法.

教師活動(dòng)小組推薦同學(xué)上臺(tái)展示和講解解題思路. 講解完,教師PPT 展示,如圖2,并提煉去分母的步驟.

圖2 解方程的兩種方法的展示圖

生: 嘗試把“分?jǐn)?shù)系數(shù)”化為“整數(shù)系數(shù)”,去掉分母.

師: 如何去分母?

生: 找到2 與5 的最小公倍數(shù)10,方程兩邊乘10.

師:“去分母”的依據(jù)是什么?

生: 等式的性質(zhì)2 等式兩邊同時(shí)乘同一個(gè)數(shù),或除以同一個(gè)不為0 的數(shù),結(jié)果仍相等.

通過(guò)問(wèn)題探究,可以得到兩種甚至更多的解法,并通過(guò)觀察比較選擇最優(yōu)解法,使得學(xué)生運(yùn)用所學(xué)的等式性質(zhì)解決問(wèn)題. 通過(guò)問(wèn)題設(shè)置,讓學(xué)生層層深入了解去分母的依據(jù)及其操作步驟.

1.3 深挖知識(shí)的歷史起源

著名的求未知數(shù)的問(wèn)題英國(guó)倫敦博物館保存著一部極其珍貴的文物——紙草書. 這是古代埃及人用象形文字寫在一種用紙莎草壓制成的草片上的著作,它于公元前1700 年左右寫成. 這部書中記載了許多有關(guān)的數(shù)學(xué)問(wèn)題,書中一道著名的求未知數(shù)的問(wèn)題.

教師活動(dòng)展示PPT,播放預(yù)錄制的視頻“萊因德紙草書的簡(jiǎn)介”,詳細(xì)的視頻文案如下:

在尼羅河三角洲盛產(chǎn)一種和蘆葦很相像的水生植物——紙莎草,古埃及人把這種草從縱面劈成小條,搗碎曬干,制作成黃色的紙頁(yè),用于寫字,便成了“紙草書”[1].

目前我們對(duì)古埃及數(shù)學(xué)的認(rèn)識(shí)與研究,主要根據(jù)兩卷紙草書,其中一卷叫《萊因德紙草書》. 它是古埃及人于公元前一千七百年左右,用象形文字記載數(shù)學(xué)問(wèn)題的著作,屬于世界上最古老的數(shù)學(xué)著作之一,現(xiàn)藏于倫敦大英博物館. 該紙草書全長(zhǎng)544 厘米,寬33 厘米. 書里列出了87 個(gè)問(wèn)題,每個(gè)問(wèn)題都給出了解答[2].

接下來(lái)我們看看在《萊茵德紙草書》中的第31 題,譯為:一個(gè)數(shù),他的三分之二,它的一半,它的七分之一,它的全部,加起來(lái)總共是33,求這個(gè)數(shù). 大家拿起筆來(lái)挑戰(zhàn)一下吧!

問(wèn)題3一個(gè)數(shù),它的三分之二,它的一半,它的七分之一,它的全部,加起來(lái)總共是33,求這個(gè)數(shù).

學(xué)生活動(dòng)學(xué)生進(jìn)行獨(dú)立思考,在導(dǎo)學(xué)案上解決該問(wèn)題.

教師活動(dòng)教師對(duì)上述視頻介紹進(jìn)行總結(jié)并引領(lǐng)學(xué)生感受數(shù)學(xué)文化的魅力. 距今3000 多年的古埃及已經(jīng)體現(xiàn)了數(shù)學(xué)問(wèn)題源于生活并于無(wú)形中服務(wù)生活.

2 聚焦知識(shí)的生長(zhǎng)

2.1 改良知識(shí)的生長(zhǎng)土壤

去分母解一元一次方程,步步都離不開(kāi)等式的性質(zhì),尤其是等式的性質(zhì)2. 等式的性質(zhì)2,等式兩邊乘同一個(gè)數(shù),或除以一個(gè)不為0 的數(shù),結(jié)果仍相等.

學(xué)生如果對(duì)此性質(zhì)理解不深刻,往往會(huì)在去分母解一元一次方程時(shí),出現(xiàn)某些項(xiàng)漏乘最小公倍數(shù),從而造成錯(cuò)誤. 在初中教師的教學(xué)中也經(jīng)歷過(guò)對(duì)學(xué)生此類的錯(cuò)誤進(jìn)行反復(fù)糾正也收效甚微. 個(gè)別老師往往會(huì)布置大量的練習(xí),希望通過(guò)“針對(duì)性”練習(xí)使得學(xué)生對(duì)此類錯(cuò)誤認(rèn)識(shí)“深刻”. 然而結(jié)果學(xué)生只是淺層知道自己漏乘是錯(cuò)誤的,但是沒(méi)有從本質(zhì)認(rèn)知為什么要各項(xiàng)乘最小公倍數(shù).

對(duì)以上的情況怎樣才是“減負(fù)提質(zhì)”的正確做法呢? 教師應(yīng)引領(lǐng)學(xué)生環(huán)視去分母解一元一次方程所需的基礎(chǔ)知識(shí),并保證學(xué)生對(duì)此有深刻而正確的理解,才能在此基礎(chǔ)上開(kāi)展新知識(shí)的建構(gòu).

問(wèn)題4根據(jù)圖3 的天平情況回答右圖的問(wèn)號(hào)處填什么?

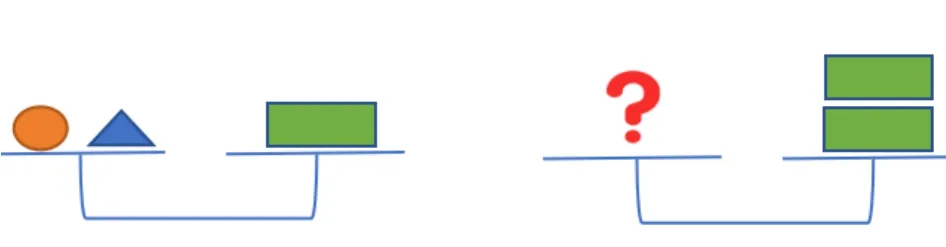
圖3 問(wèn)題展示

第一,善于用直觀的圖形替代抽象的符號(hào)表達(dá). 關(guān)于等式的性質(zhì)2 的文字和字母的表達(dá),對(duì)于七年級(jí)的學(xué)生是相對(duì)抽象的.

第二,學(xué)生看圖思考,從圖形的變化中獲得直接經(jīng)驗(yàn): 如果等式的右邊翻倍,那么左邊的圓形和三角形均需同時(shí)翻倍.

第三,學(xué)生把看圖所得經(jīng)驗(yàn)進(jìn)行推廣: 等式兩邊的各項(xiàng)均需同時(shí)乘同一個(gè)數(shù)(或除同一個(gè)不為0 的數(shù)).

第四,學(xué)生把以上總結(jié)經(jīng)驗(yàn)實(shí)施于去分母解一元一次方程的數(shù)學(xué)問(wèn)題中.

問(wèn)題5解方程.

解: 分母2 和5 的最小公倍數(shù)是10;

第①步去分母,方程兩邊同時(shí)乘10,得

化簡(jiǎn),得

第②步去括號(hào),得5x= 2x+2+6. ……分配律

第③步移項(xiàng),得5x-2x=10+2. ……等式性質(zhì)1

第④步合并同類項(xiàng),得3x=12. ……分配律

第⑤步系數(shù)化1,得x=4. ……等式性質(zhì)2

學(xué)生活動(dòng)學(xué)生能知道兩邊同時(shí)乘10,但有漏乘10.

教師活動(dòng)

(活動(dòng)一)教師引導(dǎo)學(xué)生分析方程的特點(diǎn), 把變式為,預(yù)留2 分鐘時(shí)間讓學(xué)生思考和嘗試解決.

(活動(dòng)二)教師提問(wèn)同學(xué)們此方程的解決方案,同時(shí)黑板書寫例題的解答過(guò)程,邊問(wèn)邊寫.

提問(wèn)1: 為什么方程兩邊乘的這個(gè)數(shù)是10?

提問(wèn)2: 為什么方程兩邊要乘10?

提問(wèn)3: 沒(méi)有分母,它是否需要乘10? 為什么?

2.2 指引知識(shí)的生長(zhǎng)方向

研讀教材第97 頁(yè)發(fā)現(xiàn)每一次“去分母”后都會(huì)在相應(yīng)的分子處添括號(hào),此處教師可指引學(xué)生發(fā)現(xiàn)問(wèn)題并思考此問(wèn)題的內(nèi)涵.

問(wèn)題6在中的分?jǐn)?shù)線有什么意義和作用?

學(xué)生活動(dòng)學(xué)生回答分?jǐn)?shù)線的意義為除號(hào).

教師活動(dòng)教師介紹分?jǐn)?shù)線的雙重含義: 除號(hào)和括號(hào).分?jǐn)?shù)線分隔分子分母,實(shí)質(zhì)上是一個(gè)隱形的括號(hào),因此去分母后,分?jǐn)?shù)線消失了,仍要保持原式不變,必須在原來(lái)分子處添加括號(hào). 通過(guò)經(jīng)典問(wèn)題,展示去分母解一元一次方程的規(guī)范解答及兩個(gè)易錯(cuò)問(wèn)題強(qiáng)化了學(xué)生對(duì)等式性質(zhì)2 和分配律的理解,使得教與學(xué)都非常高效.

2.3 梳理知識(shí)的生長(zhǎng)脈絡(luò)

問(wèn)題7你能否總結(jié)本題的解題步驟及其思想方法?

學(xué)生活動(dòng)學(xué)生根據(jù)自己的理解回答問(wèn)題.

教師活動(dòng)教師PPT 投影例題中解方程的流程圖,如圖4,通過(guò)實(shí)例總結(jié)解一元一次方程的一般步驟及其依據(jù).

圖4 本節(jié)課的課堂總結(jié)

通過(guò)梳理一元一次方程的解答流程圖,進(jìn)一步鞏固解一元一次方程的“五步法”,同時(shí)滲透程序化和化歸的數(shù)學(xué)思想方法;通過(guò)總結(jié)解一元一次方程過(guò)程,總結(jié)“化歸”的數(shù)學(xué)思想,有利于學(xué)生理解和掌握重要的數(shù)學(xué)思想方法.

3 體驗(yàn)高效的教學(xué)

3.1 教師高效的教學(xué)體驗(yàn)

教師在備課時(shí)做大量“根”的研究,關(guān)注學(xué)生知識(shí)起點(diǎn)、關(guān)注知識(shí)的根系,關(guān)注知識(shí)的歷史起源,從而使得課堂的授課起點(diǎn)與學(xué)生的知識(shí)水平無(wú)縫銜接, 實(shí)現(xiàn)課堂的精準(zhǔn)定位,教師的高效講解.

教師在評(píng)價(jià)學(xué)生時(shí)利用信息技術(shù)進(jìn)行收集學(xué)生的學(xué)情,無(wú)論在課前抑或課后均可實(shí)施. 本課使用點(diǎn)陣筆技術(shù)反饋學(xué)習(xí)效果的試題設(shè)計(jì),如圖5. 教師首先在網(wǎng)頁(yè)導(dǎo)入預(yù)設(shè)計(jì)的試題,試題設(shè)計(jì)做到每題考查的知識(shí)和方法清晰明了,然后學(xué)生用簽字筆限時(shí)作答,最后教師回收試題并用點(diǎn)陣筆進(jìn)行批改,對(duì)應(yīng)平臺(tái)上就獲得即時(shí)數(shù)據(jù)分析. 利用信息技術(shù),實(shí)現(xiàn)學(xué)情的精準(zhǔn)把控,教師的高效評(píng)價(jià).

圖5 點(diǎn)陣筆技術(shù)賦能的課堂即時(shí)反饋題目

3.2 學(xué)生高效的學(xué)習(xí)體驗(yàn)

學(xué)生在學(xué)習(xí)過(guò)程中,通過(guò)問(wèn)題的引領(lǐng),層層遞進(jìn),逐漸逼近數(shù)學(xué)的本質(zhì),掌握數(shù)學(xué)的思想方法. 學(xué)生高效的學(xué)體現(xiàn)在以小見(jiàn)大,如問(wèn)題1、問(wèn)題4、問(wèn)題6,通過(guò)小細(xì)節(jié)的觀察和理解可以獲得大道理. 其次,學(xué)生高效的學(xué)體現(xiàn)在舉一反三,問(wèn)題5 是經(jīng)典例題,可以達(dá)到以一敵百的效果. 這是脫離茫茫題海,真正實(shí)現(xiàn)減負(fù)提質(zhì)增效.

4 結(jié)束語(yǔ)

聚焦知識(shí)的生與長(zhǎng),實(shí)現(xiàn)了化歸思想的滲透,并將“追求簡(jiǎn)單化”這一數(shù)學(xué)的靈魂貫穿課堂始終. 基于數(shù)學(xué)的簡(jiǎn)潔性和概括性的本質(zhì)要求,設(shè)計(jì)了相應(yīng)的內(nèi)容. 探究問(wèn)題的兩種方法比較制造認(rèn)知沖突,凸顯數(shù)學(xué)的靈魂“追求簡(jiǎn)單化”. 經(jīng)典例題涵蓋方法和常見(jiàn)易錯(cuò)點(diǎn),希望能夠?qū)崿F(xiàn)“以一敵百”的能力目標(biāo). 巧用教材,通過(guò)深挖教材案例的歷史背景,搜索史料,獨(dú)立制作一段關(guān)于《萊茵德紙草書》的中文視頻,滲透數(shù)學(xué)文化,體會(huì)數(shù)學(xué)來(lái)源于生活并應(yīng)用于生活,數(shù)學(xué)是非常有用的! 設(shè)計(jì)針對(duì)性問(wèn)題及利用點(diǎn)陣筆收集數(shù)據(jù),及時(shí)了解學(xué)生掌握情況,調(diào)整教學(xué)策略,實(shí)現(xiàn)精準(zhǔn)反饋. 聚焦知識(shí)的生與長(zhǎng),才能貫徹落實(shí)“雙減”政策,體驗(yàn)高效的教與學(xué).