一類對稱雙線性型下三對角矩陣特征值的譜分隔性質

徐偉孺

(四川師范大學 數學科學學院，四川 成都 610066)

0 引言

高等代數中介紹了雙線性型的一些基礎概念，其本質就是兩個變量分別線性的二元函數V×V→F，其中F是給定的域，V是F上的線性空間[1]。本文考慮了一個對稱雙線性型Rn×Rn→R，其定義形式為

其中x,y ∈Rn，且H是一個對稱的正交矩陣。對于給定的n階實矩陣A，存在其伴隨算子A#使得對于任意的向量都有〈Ax,y〉H=〈x,A#y〉H成立。此時，A#=HATH.若A#=A，A就稱為H-對稱或者偽對稱矩陣，其含義其實就是內積(1)里面的對稱矩陣，區別于H為n階單位矩陣In時的歐式內積情形。類似地，若A#A=In，矩陣A就是H-正交或者偽正交的[2]。

當矩陣A為n階不可約的三對角矩陣時，對于矩陣H的不同形式，矩陣A將會有不同的性質。最常見情形就是：H=In，矩陣A就是不可約的對稱三對角矩陣，其特征值是互異的實特征值，并與其主子矩陣的特征值嚴格交錯[3-4]。其特征值問題的討論很廣泛，也比較成熟[5-9]。但在閔可夫斯基空間中存在一類符號算子H=In⊕-I1，矩陣A就是偽對稱的[10-13]，形如

其特征值不同于對稱矩陣的特征值，可能含有成對的共軛復特征值。現在介紹一種特殊情形，就是當(2)式中的矩陣A的特征值全部為互異實數時，給定矩陣A一個秩1 擾動=A+teneTn，其中t＜0 且en為單位矩陣In的第n列。下面就給出兩個問題：

問題2 矩陣A與的特征值之間的譜分隔性質如何？

定理1已知形如(2)式的矩陣A和其擾動矩陣=A+teneTn，t＜0，且其特征值分別為λi，i=1,2,…,n和μi,i=1,2,…,n。假 設λ1＜λ2＜…＜λn，則矩陣的特征值μi全部為互異的實數，并滿足如下的嚴格交錯性質：

1 定理的證明

由于(2)式的矩陣A是一個非自伴的三對角矩陣，其相似于一個下次對角線元素全為正的矩陣，且具有相同的符號算子H=In-1⊕-I1，在文獻[14]中，其相似矩陣稱為偽Jacobi 矩陣。在證明定理1 之前，需要介紹如下的引理。

引理1[14]已知A為形如(2)式的矩陣且具有互異的實特征值λi,i=1,2,…,n，則矩陣A可被H-對角化，即Q#AQ=Λ=diag(λ1,λ2,…,λn)，且其H-正交矩陣Q的第一行和最后一行的元素均非零。

約定Q=[q1,q2,…,qn]T,其中qi=[qi1,qi2,…,qin]T。下面給出定理1 詳細的證明。

從而矩陣A和沒有相同的特征值。因此，的特征值μi是如下特征方程的根：

很明顯，上述兩個函數的交點就是S(λ)的零點。函數f(λ)的n個互異的極點(或間斷點)將實數域R 分成了n+1 個區間，分別是(-∞,λ1)，(λi,λi+1),i=1,2,…,n-1，和(λn,+∞)。函數f(λ)在這些區間內均連續，其圖形變化情況如下：

由(iii) 可知，函數f(λ)在每個小區間(λi,λi+1),i=1,2,…,n-2 內至少與函數g(λ)有一個交點，故可確定函數f(λ)和g(λ)的圖象在這些小區間內至少有n-2 個交點。

由(i)和(ii)可知，函數f(λ)和g(λ)的圖象在這兩個無限區間內分別至少有一個交點。從而就確定了函數f(λ)和g(λ)至少有n個交點。而函數S(λ)至多只有n個根。故函數f(λ)和g(λ)只有n個交點，在(λn-1,λn) 內，它們不相交。此時，函數S(λ)的零點μi,i=1,2,…,n全為實數，且與其極點的關系滿足：

證畢。

下面給出兩個實例，驗證擾動前后特征值之間的交錯情況。

例1給定一個如下的形如(2)式的矩陣

參數t的值t=-0.0 001，計算矩陣A和的特征值，如下表：

表1 矩陣A 和的特征值

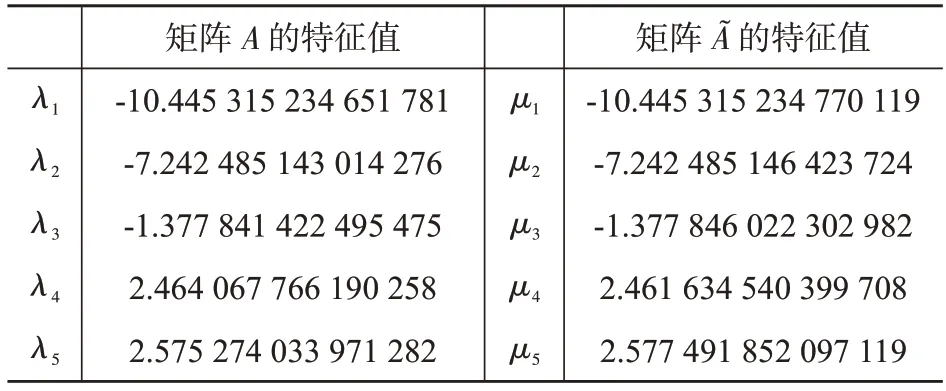
表1 矩陣A 和的特征值

從計算結果可知，矩陣A和的特征值之間滿足定理1 給出的交錯不等式的關系。

另外，為了說明滿足本文給出的交錯不等式的兩組譜可以是矩陣A和擾動后的矩陣的特征值，故給出如下的例子。

例2 給 定λ1=-3,λ2=1,λ3=3;μ1=-4,μ2=-1；μ3=7。

很明顯，上述數據滿足定理1 給出的交錯不等式。它們分別是矩陣Α 和的特征值。

因而，滿足本文的交錯不等式的兩組數據可以是矩陣A和的特征值，這兩個矩陣只是最后一個對角元互異。從而可以繼續研究這類矩陣的重構造問題。

2 結論

本文在對稱雙線型中討論了具有形式(2)的矩陣與其秩1 擾動矩陣的特征值之間的譜分隔性質，得出了一個嚴格的交錯不等式。對于其它形式的偽對稱三對角矩陣，不能得出比較好的譜分隔性質，只是用公式籠統的表示出來。比如文獻[15-16]，給定的是任意的符號算子，這樣就不方便來討論類似本文的特征值之間的交錯性質。討論這個性質的本質不是出于數學的興趣，它對于重構造一個具有形式(2)的矩陣和提供很好的理論依據，廣泛的應用于非Hermitian 量子力學中薛定諤方程的離散和截斷化[17]，不定Toda 晶格的哈密爾頓系統的重構[18-20]等。這種帶有任意的符號算子Η 的三對角矩陣的特征值問題或反特征值問題不同于對稱三對角矩陣的情形，Η 中任意符號的改變將會引起矩陣Α 的特征值產生較大的變化。