基于模型與數據相結合的列車牽引電機定子電流估算方法

摘要 定子電流是實現牽引電機閉環控制與狀態監測的關鍵信號。在已知牽引力與速度信息的情況下，實現對定子電流的估計是牽引電機異常檢測與狀態預測的重要環節，為此文章提出了一種基于模型與數據相結合的列車牽引電機定子電流估算方法，首先通過分析牽引電機數學模型，初步實現對定子電流的估計；然后以列車速度、牽引力與模型估計的定子電流為輸入、實際電流為輸出，充分考慮不同工況下電機的工作特性，將電機工作劃分為啟動、牽引、制動與惰行等四種工況，分別建立了基于反向傳播（Back Propagation，BP）神經網絡的電機定子電流估計模型；最后基于列車的實際運行數據，驗證了所提模型的有效性和可行性。

關鍵詞 牽引電機；定子電流估算；數據與機理的混合估計模型

中圖分類號 U279 文獻標識碼 A 文章編號 2096-8949（2024）24-0033-04

0 引言

高速列車是重要的交通工具[1]，電力牽引傳動系統是其唯一的動力來源，由牽引電機、牽引變壓器、牽引變流器、牽引電機等組成[2]。牽引電機將牽引系統從電網獲得的電能轉化為動能，其定子電流與磁鏈和電磁轉矩緊密關聯。在牽引電機控制中，一般采用直接轉矩控制或矢量控制，定子電流是實現閉環控制的關鍵指標[3]。通過對定子電流的精確計算和實時監控，能夠確保電機在不同工況下維持最佳的運行狀態，提高列車的加速性能、穩定性及整體運行效率[4]。此外，定子電流的變化也能反映電機的運行狀況及潛在故障，提供早期預警信息，因此對其進行有效估算不僅有助于提升運行效率，還對列車的故障預測與預防性維護具有重要價值。

目前，對于異步電機的電流估計問題，已有很多研究成果發表。肖明[6]基于空載電流與額定電流之間的關聯關系，提出了一種三相異步電動機空載電流的解析計算方法；霍大勇[7]討論了異步電動機額定電流與空載電流的關系，實現了電機空載電流的估算方法；陳金剛[8]通過對電機空載試驗與堵轉試驗數據進行統計分析，總結了空載電流、堵轉電流與額定電流之間的數量關系；程小華[9]基于理論推導與具體案例分析，提出了一種基于毛估計法的三相異步電機額定電流的估算方法。然而，電機在實際運行過程中，其定子電流受負載變化、環境因素及工況復雜性等多重因素的影響，表現出顯著的非線性變化特征。傳統的電流計算方法基于線性模型、假設工況，難以適應復雜多變的運行環境，導致估算精度不足。此外，由于電機的非線性動態特性強，尚不存在一個通用的解析公式能夠精準描述電機定子電流在不同負載條件下的變化規律。因此，如何有效地應對電機電流的非線性變化，提出一種適應性強且高精度的估算方法，已成為亟待解決的問題。

針對僅知列車線路規劃的牽引力與速度信息的實際應用場景，提出了一種基于反向傳播（Back Propagation，BP）神經網絡與機理模型相結合的電機定子電流估算方法。該方法首先通過分析電機數學模型，建立已知牽引力與速度信息的定子電流估計模型，其次分析電機運行工況特性，分別討論列車的啟動、牽引、惰行與制動等四種工況，然后基于模型估計的定子電流模型、規劃數據與實際測量的電流歷史數據樣本，分工況挖掘它們之間的非映射關系，建立基于BP神經網絡的定子電流估計模型，最后基于現場運行數據，進行實驗驗證。結果表明，該文提出的方法，相比于模型估計方法提升了電流的估計精度，更加適合工程實踐。

1 牽引電機定子電流的機理模型分析

文獻10提出了一種牽引電機定子電流的機理模型。該模型以當前速度和轉矩為基礎進行構建，其表達式如下：

（1）

式中，Rr——轉子電阻（?）；ωsl——轉差角頻率

（rad/s）；Lr——轉子等效自感（mH），為互感Lm與轉子漏感Llr（mH）；Np——電機極對數；Te——電機當前轉矩（N·m）。

其中，轉差角頻率ωsl需計算得出，其計算表達式如下：

（2）

式中，s——異步電機的轉差率（%）；n——電機轉速（r/min）。轉差率s的計算表達式如下：

（3）

式中，k——電機轉矩Te與轉差角頻率ωsl間的轉換系數，由該文牽引電機的特性參數表與實驗數據的擬合分析得到，該文選用機型對應k的數值為0.0 938；——定子磁鏈給定值，在實際工程應用中，額定轉速以下通常采用恒磁通的控制策略，以確保電機性能的穩定；而在額定轉速以上，則采用弱磁控制策略，以適應高速運行的需求，故可通過試驗數據擬合求得定子磁鏈給定值與轉速之間的關聯曲線。

首先將電機當前的轉速n和轉矩Te作為輸入參數，代入式（3）中計算轉差率s，然后通過式（2）求出此刻電機的轉差角頻率ωsl，最后基于式（1）計算得到機理模型下電機定子的電流估算值。

2 BP神經網絡與機理模型相結合的定子電流估計模型

2.1 BP神經網絡原理

BP神經網絡，以其獨特的算法結構和強大的學習能力，在機器學習領域具有廣泛的應用價值。BP神經網絡由輸入層、隱藏層和輸出層等三層組成。BP神經網絡傳播包含兩個過程[11]，其一是信息正向傳播，其二是誤差反向傳播。

信息正向傳播的過程如下：

數據從輸入層到隱藏層

（4）

式中，M——輸入層層數；wij——第i個節點和第j個節點之間的連接權值；xj——第j個節點的輸入函數；——第i節點的閾值。

數據從隱藏層到輸出層

（5）

（6）

式中，——節點的輸出函數；q——隱藏層變量數量；ak——第k個節點的偏置。

數據從輸出層輸出

（7）

式中，——激勵函數。

其中，誤差反向傳播的過程如下：

對輸出層進行運算后，利用誤差函數對該系統進行誤差計算，誤差函數E的表達式如下：

（8）

式中，L——輸出層層數；Tk——第k個節點的實際

值；Yk——第k個節點的估計值。

誤差反向傳播機制的作用在于通過多次迭代，持續地對神經網絡中各節點間連接的權重進行調優，旨在逐步減小誤差，直到符合預期要求。

2.2 BP神經網絡與機理模型混合建模

為了對電機的定子電流進行實時估算，需先離線建模得到各工況下的BP神經網絡。離線建模階段：基于歷史數據離線，每個工況訓練一個BP神經網絡，神經網絡的輸入數據為電機的轉矩Te、轉速n，以及基于式（1）～（8）計算的定子電流估算值，輸出數據為定子電流實測值Is。在得到各工況下的BP神經網絡后，將模型導入在線計算階段，實時輸入電機的轉矩Te、轉速n，然后實時判斷工況和計算定子電流估算值，最后根據工況選擇對應的訓練完成的神經網絡進行實時估算。整個估算法的原理框圖如圖1所示：

3 實驗驗證

3.1 實驗描述

為了驗證所提的定子電流估計模型的有效性，該文以某自動駕駛汽車在某時間段的現場實測數據為例，與模型方法進行對比實驗研究。其中，實測數據包括自動駕駛系統（Automatic Train Operation，ATO）裝置輸出的規劃牽引制動力（Te）、規劃速度（n），以及中央控制單元（Central Control Uni， CCU）記錄的電機電流有效值；采樣周期為100 ms，包含啟動、牽引、惰行與制動四個工況。

為了評估該預測模型的有效性及預測性能的優劣，該文采用均方根誤差（Root Mean Square Error， RMSE）作為模型評價指標，可表示如下：

（9）

式中，和Y——模型的估算電流值和電流實測值；N——樣本數。

3.2 實驗分析

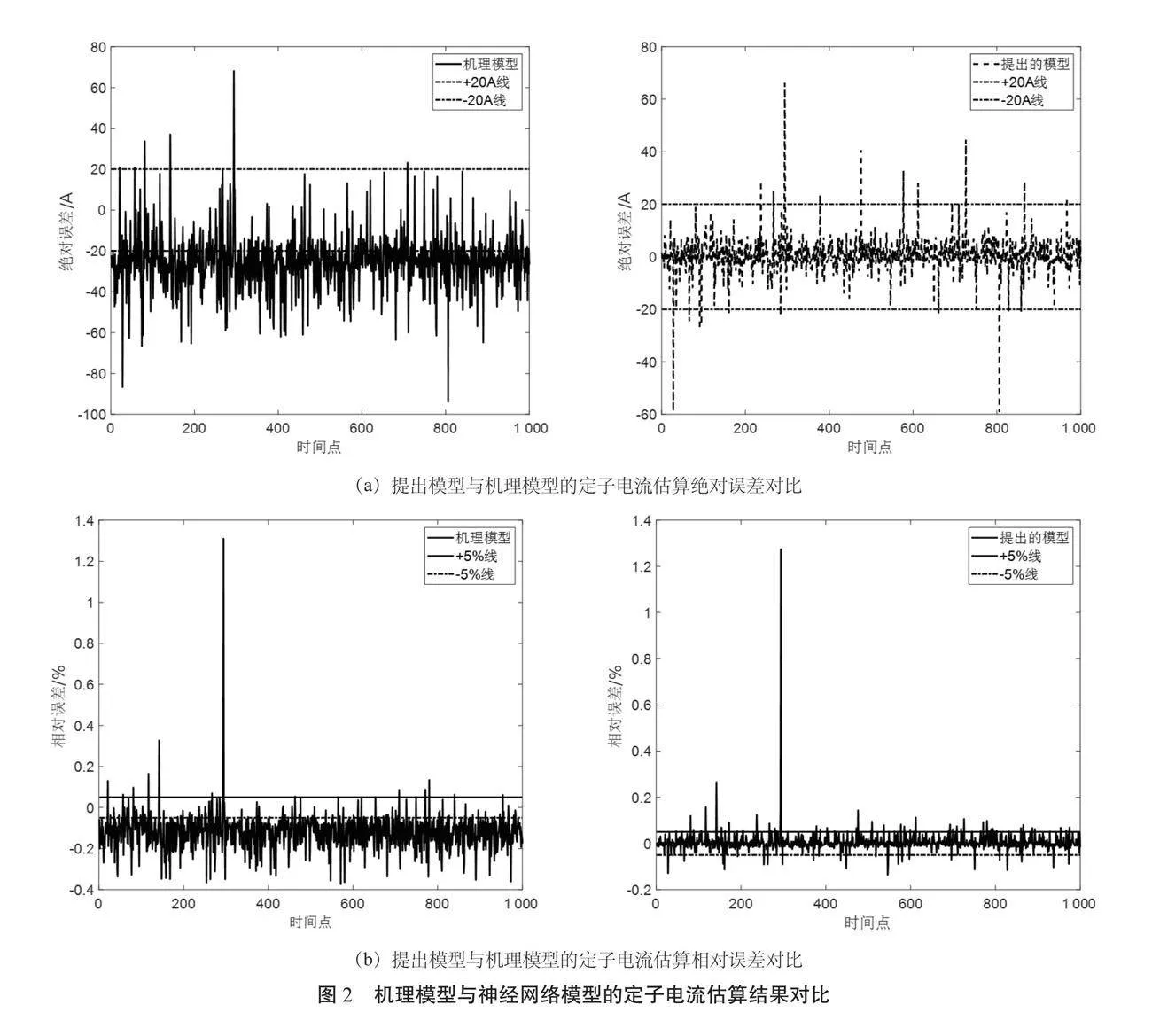
如圖2所示，基于現場實際運行案例為樣本，包含列車運行時的啟動、牽引、惰行與制動等四種工況。相比機理模型，混合模型能夠更好地擬合定子電流。由圖2（a）可知，該文提出的混合模型定子電流估計值與實際值的絕對誤差基本在20 A以內，明顯小于模型法的估計誤差；由圖2（b）可知，該文提出的混合模型定子電流估計值與實際值的估計相對誤差基本在額定電流的5%內，同樣顯著低于模型法的估計誤差，能夠滿足工程實踐的需要，表明該文提出方法的有效性。

采用均方根誤差（RMSE）指標評估各模型在各工況下的定子電流估計效果。由表1可知，牽引和制動工況時BP神經網絡模型的RMSE最大值不大于10 A，遠小于基于機理模型的方法。在啟動工況和惰行工況時，BP神經網絡模型的RMSE值變大，但仍優于基于機理模型的方法。

4 結語

該文針對在僅已知規劃牽引力與速度的情況下，對牽引電機定子電流的估計問題展開研究，提出了一種基于牽引電機數學模型與BP神經網絡相結合的定子電流實時估算方法，并通過采集和應用現場實際的運行數據進行驗證。研究結果表明，在列車牽引與制動這兩種典型工況下，采用基于BP神經網絡的估算方法所得的定子電流值與實際測量值基本一致，表現出良好的估算性能；在列車啟動和制動這兩個瞬態工況中，由于電流波動較大且變化復雜，該文所提出的定子電流估算法的誤差相對較大，需要在后續研究中針對這些特殊工況進行優化和改進。

參考文獻

[1]國家鐵路局.我國鐵路營業里程達15.9萬公里復興號開行實現31個省份全覆蓋[J].中國環境監察， 2024（1）：8.

[2]張朝輝，秦帥，趙震，等.神華八軸電力機車牽引傳動系統[J].鐵道機車車輛， 2019（6）：37-40+49.

[3]羅建濤．機車逆變過流故障診斷研究與應用[J].機車電傳動， 2018（5）：78-82．

[4]蔣奉兵.列車牽引系統過流故障在線診斷與處理技術研究[D].長沙：湖南大學， 2020.

[5]李學明，徐紹龍，倪大成，等.基于時序特征模式識別的牽引電機過流實時診斷[J].電機與控制應用， 2021（10）：77-83.

[6]肖明．三相異步電動機空載電流估算[J].中小型電機， 1990（6）：19．

[7]霍大勇．380V籠型交流異步電動機額定電流與空載電流的估算[J].礦山機械， 2008（20）：100-102．

[8]陳金剛．籠型三相異步電動機的空載和堵轉電流[J].電機技術， 2016（5）：35-37．

[9]程小華．毛估法之用于異步電動機額定電流的估算[J].防爆電機， 2019（5）：1-3．

[10]徐紹龍，倪強，李學明，等.自動駕駛電力機車牽引變流器中IGBT壽命損耗優化策略[J].中國電機工程學報， 2021（18）：6381-6390.

[11]金建峰，高健.基于神經網絡的電力短期負荷預測方法研究[J].能源與節能， 2023（7）：41-44.