混合梁斜拉橋邊跨現澆混凝土箱梁抗裂性分析

摘要 為進行獨柱式塔混合梁斜拉橋邊跨混凝土梁的受力性能分析，研究其設計的關鍵問題。文章以某高速公路獨塔斜拉橋為依托，通過理論分析、數值模擬、對比優化相結合的方法對邊跨混凝土梁的抗裂性及受力特點進行了研究。研究表明，原設計邊跨混凝土主梁具有良好的抗裂性能，但由于混凝土預應力度較高，在箱梁底板出現較大的橫向壓應力；降低橫向預應力的型號優化后，混凝土箱梁的壓應力得到了有效緩解，受力更加合理；對于分離式混凝土梁設計時，應合理控制預應力度，避免箱梁底板出現壓應力過大。

關鍵詞 鋼箱梁；分段拼裝；頂推施工；施工技術

中圖分類號 U445 文獻標識碼 A 文章編號 2096-8949（2024）24-0109-03

0 引言

斜拉橋是一種由主梁、橋塔和拉索組成的組合體系結構，具有良好的承載能力和跨越能力，廣泛應用在跨江跨河工程中[1]。根據結構形式的不同和材料類型的不同，有很多種不同的分類方式。其中，獨塔混合梁斜拉橋是一種結構體系相對較為新穎的斜拉橋結構形式[2-3]。這種結構形式既滿足了單側跨越障礙物的要求，又充分利用兩種材料重量的不同進行橋面搭配，兼顧了跨越能力和經濟性控制的要求。

現有針對獨塔混合梁斜拉橋的相關研究主要針對混合梁斜拉橋的合理結構布置、關鍵構造、塔梁連接的合理結構形式等方面開展[4-5]。有學者對獨塔斜拉橋的合理邊中跨比例進行了研究[6]，也有學者對是否設置輔助墩進行了分析[7]。塔梁連接形式，以及拉索與主梁、主塔連接的關鍵構造也有較多的研究開展。這些研究多針對整體箱形斷面的研究，而針對獨柱式塔、分離式雙主梁體系的混合梁獨塔斜拉橋的相關研究則相對較少[8-9]。

對于分離式雙主梁的混合梁斜拉橋而言，由于邊跨混凝土梁的橫向尺寸較大，構造和受力均較為復雜，在設計過程中對邊跨混凝土梁的受力控制是關鍵。一旦控制不佳，混凝土梁極易出現開裂等病害。為了對柱式塔分離式混合梁獨塔斜拉橋的邊跨混凝土抗力性能進行分析，并研究其受力特點，該文以某高速公路大跨度混合梁獨塔斜拉橋為依托，開展了相關研究。

1 工程概況

1.1 總體概況與建設條件

依托工程為某高速公路跨河大橋工程，該項目為標準雙向四車道高速公路，標準路基寬度為25.5 m，橋梁區段采用分離式路基布置。

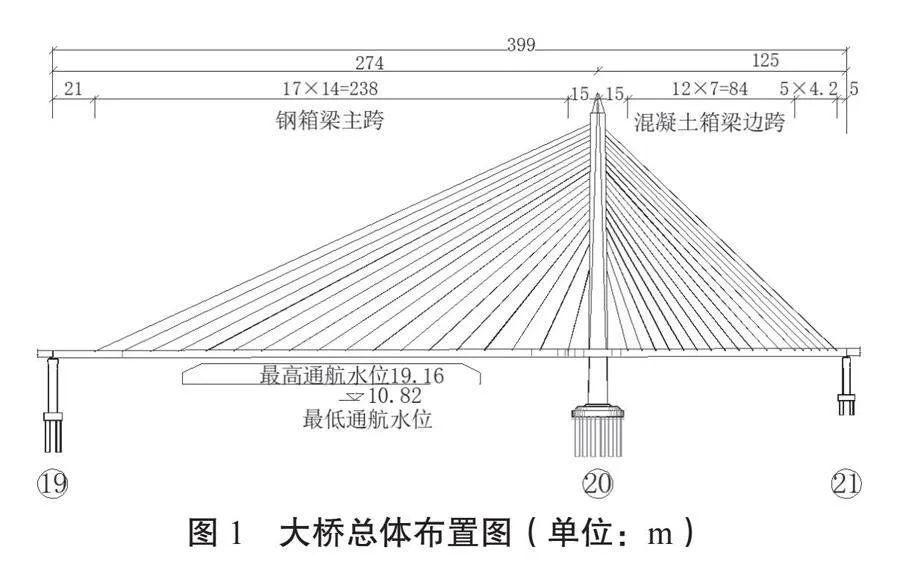
大橋主橋為柱式獨塔空間雙索面混合梁斜拉橋，塔梁固結型式，由索塔兩側的246 m和125 m橋跨組成。大橋的總體布置圖如圖1所示，中跨為鋼箱梁結構，邊跨為混凝土箱梁結構，鋼混結合段設置在距離橋塔中心線16 m的中跨處。主梁和主塔之間通過16對拉索進行連接，拉索采用空間索面扇形布置，鋼梁側拉索間距為14 m，混凝土側拉索標準間距為7 m，靠近過渡墩位置

4對拉索間距為4.2 m。根據邊中跨鋼梁和混凝土梁重量的不同，適配了不對稱的獨塔布置形式。

大橋主塔采用獨柱式索塔結構，構造挺拔美觀，主梁采用分離式雙主梁結構形式，分別布置在橋塔的兩側。主塔總高度為160 m，截面為八邊形漸變形式，棱角分明，結構美觀。

圖1 大橋總體布置圖（單位：m）

1.2 結構特點

主梁采用混合梁形式，中跨鋼梁和邊跨混凝土梁外觀保持一致，鋼混結合段采用前承壓板帶格式的結合段形式，鋼混結合段長度為3.2 m，鋼梁標準段長度為14 m，邊跨混凝土邊跨分三段澆筑，采用少支架體系現澆施工，主梁之間采用澆筑濕接縫進行連接，并逐段張拉斜拉索及主梁內的體外預應力。

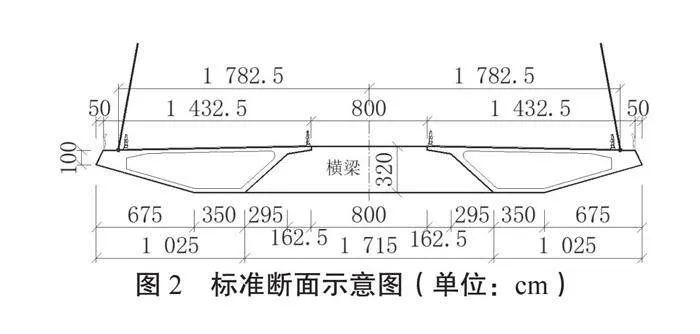
混凝土主梁的標準斷面示意圖如圖2所示，采用分離式布置，橋面設置雙向橫坡，主梁內側高度為3.2 m，兩個主梁之間采用箱形預應力混凝土橫梁進行連接，對橫梁進行等高度布置。兩副主梁之間的橫梁縱向間距應與邊跨側拉索布置間距保持一致。

混凝土主梁采用扁平流線形布置，單個主梁底板寬度為10.25 m，頂板寬度為14.825 m，內側梁高度為3.2 m，外側錨索區梁高度為1.0 m。兩幅箱梁之間的凈距為8 m，斷面總寬度為37.65 m。

圖2 標準斷面示意圖（單位：cm）

2 計算模型與分析方法

2.1 計算模型

該研究中利用大型通用有限元軟件ANSYS，對該區域建立三維實體模型，分析其在最不利工況下的結構狀態，并對該區域設計提出合理的優化建議。

采用大型有限元軟件ANSYS建立混凝土邊跨段實體模型。主梁使用Solid45單元，體外預應力采用link8單元。在實際建模過程中，選取距索塔中心11.5～124.9 m

的邊跨支座處為對象進行建模，計算模型如圖3所示：

圖3 鋼梁橫向分塊示意圖

計算時為真實模擬邊跨的受力情況，以及固結靠近索塔梁端的邊跨支座的支撐效果，通過計算得到支座反力，以荷載的形式直接施加在模型上。根據圣維南原理，僅在固結端小范圍內的梁體受力失真，隨著遠離固結端，梁體受力更加符合實際情況。

2.2 荷載與邊界條件

考慮此次分析混凝土邊跨局部的構造復雜、構件多、建模復雜、工作量大等情況，結合此次研究的主要目的，在模型節段選取、荷載和邊界條件確定上進行了精心考慮。計算中建立了多個計算模型，相互對照，確保結構分析準確。為了能與設計對比總體的計算結果，利用Midas Civil程序建立梁單元計算模型，進行總體計算，以提供局部分析可對照和比較的邊界條件。另外，為了能真實模擬混凝土邊跨，選取距離索塔中心11.5～124.9 m

段的主梁進行建模分析。在計算分析的過程中，假設實體模型中的預應力鋼束與混凝土箱梁之間無滑移，并采用預應力節點與混凝土單元耦合的方式實現兩者的連接。

邊跨最不利工況以其彎矩影響線為依據，選取彎矩最大的斷面為參考，首先基于Midas梁單元計算模型，確定上述最不利工況下局部實體模型活載，對線加載位置和荷載空間內力邊界條件的影響。基本方法是通過對混凝土邊跨荷載效應的研究，確定距邊跨遠端43.4 m處斷面發生最不利受力狀態時局部模型的活載施加位置，并以這一內力狀態作為局部分析時荷載控制的邊界條件。

3 鋼箱梁頂推施工

3.1 原方案受力狀態分析

考慮收縮、徐變等作用，橫向預應力在張拉后會產生預應力損失等效應，在混凝土主梁結構自重、二期鋪裝、斜拉索索力和汽車荷載等作用下，混凝土邊跨有限元計算結果表面邊跨混凝土箱梁具有良好的抗裂性能，最大主拉應力不超過1.5 MPa。邊跨整體的壓應力較為均勻，在7～14 MPa之間。整體上橫梁處于受壓狀態，且底部壓應力大于頂部，B形橫梁底部壓應力較大，而A形橫梁受力狀態良好。B形橫梁的混凝土底板主壓應力如圖4所示，由壓應力分布情況可知，在與B形橫梁相連接的底板位置出現較大壓應力，接近于20 MPa。該位置的壓應力水平較高，需要對橫梁的橫向預應力進行優化。

圖4 B形橫梁的混凝土底板主壓應力（單位：MPa）

3.2 橫向預應力優化

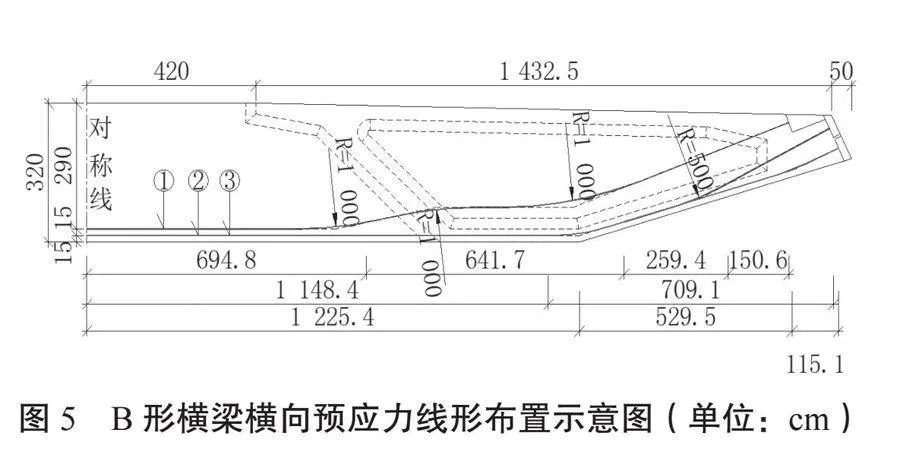
由于箱梁底板的橫向預應力較大，因此在預應力優化過程中主要考慮將橫向預應力適當降低，主要考慮兩種優化方案：方案一，在原有設計基礎上，將B形橫梁的2號預應力鋼束改為Φs15.2-21；方案二，將B形橫梁的1號、2號和3號預應力鋼束均改為Φs15.2-21。其中，B形橫梁的橫向預應力線形布置示意圖如圖5所示，1～3#鋼束均布置2根。

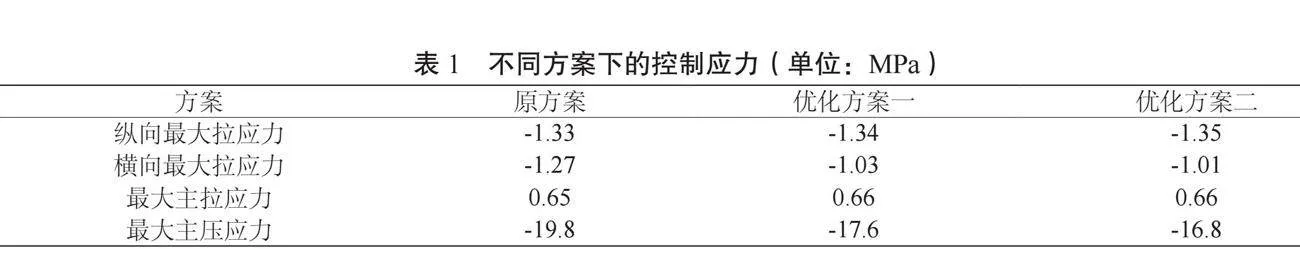
調整預應力鋼束后，在自重、二期鋪裝、索力和汽車荷載等作用下，混凝土邊跨箱梁的有限元計算分析結果的對比情況如表1所示：

從表1分析可知，在三種橫向預應力布置情況下，箱梁的縱橫向均處于受壓狀態，具有良好的抗裂性能。混凝土箱梁出現的主拉應力均在1 MPa以內，均小于混凝土的抗拉設計強度，不會出現開裂現象，均滿足抗裂性要求。

從混凝土的主壓應力對比情況可知，優化方案二的主壓應力最大值可控制在-16.8 MPa，最大壓應力值在規范允許的范圍內，可有效避免混凝土內出現過大的壓應力。按照優化方案二，將B形標準橫梁預應力鋼束1～3#的型號由原來的Φs15.2-25調整為Φs15.2-21更為合理，在滿足抗裂性的同時，壓應力也在合理范圍內。

4 結束語

為了對構造復雜的混合梁斜拉橋邊跨混凝土梁的抗裂性進行研究，以了解其受力特點，并對其預應力鋼束進行優化，以獲得良好的受力狀態，通過系統的有限元模擬與優化分析，可以得到以下結論：

（1）采用了總體模型與局部模型相結合的混合分析方法，對混合梁斜拉橋的邊跨受力性能進行了研究，發現荷載邊界的等效能夠滿足計算精確性和計算效率的要求。

（2）原設計邊跨混凝土主梁具有良好的抗裂性能，滿足使用階段的抗裂性要求，但由于混凝土預應力度較高，在箱梁底板出現較大的橫向壓應力。

（3）通過優化對比分析，降低了橫向預應力的型號，改善了箱梁底板的最大預應力，使得混凝土箱梁的受力更加合理。

（4）在箱梁結構設計時，除主要考慮橫梁自身的受力狀態外，還應考慮橫向預應力對橫梁連接區域箱室結構的影響，合理控制預應力度，避免箱梁底板出現壓應力過大。

參考文獻

[1]魏一絎.獨塔混合梁斜拉橋施工過程分析[D].成都：西南交通大學， 2015.

[2]陳宇.獨塔混合梁斜拉橋受力分析研究[D].成都：西南交通大學， 2008.

[3]李輝，夏飛龍.獨塔混合梁斜拉橋設計研究[J].黑龍江交通科技， 2023（3）：76-79.

[4]肖勇剛，張巍.獨塔混合梁斜拉橋成橋階段索力優化研究[J].公路與汽運， 2023（2）：87-90.

[5]冉久黌.大跨度寬幅獨塔混合梁斜拉橋主梁正應力分布規律研究[D].重慶：重慶交通大學， 2023.

[6]周子杰，阮欣.獨塔混合梁斜拉橋無索區影響及合理確定方法[J].結構工程師， 2013（6）：44-48.

[7]王海山.獨塔混合梁斜拉橋施工仿真分析與控制技術研究[D].南京：東南大學， 2014.

[8]陳孔亮，葉健新，徐郁峰，等.獨塔混合梁斜拉橋參數靈敏度分析[J].中外公路， 2024（2）：182-190.

[9]姜長宇，李凱，吳波，等.輔助墩對大跨獨塔混合梁斜拉橋力學性能的影響[J].黑龍江交通科技， 2019（12）：120-122+124.