淺析物理類專業(yè)高等數(shù)學教學中的難點與策略

摘?要：高等數(shù)學是理工科非數(shù)學類專業(yè)的重要基礎課，是其他專業(yè)課的先行課程。高等數(shù)學內(nèi)容涉及廣泛、重難點突出、教學難度高。物理類專業(yè)對高等數(shù)學課程的要求則尤為顯著，究其原因，主要體現(xiàn)在其專業(yè)課難度方面。本文簡要分析了物理類專業(yè)課程關(guān)于數(shù)學運用方面的重難點，主要包含概念多、概念抽象、控制方程復雜等方面，提出了相應的高等數(shù)學教學策略，主要包含借助物理實例闡釋數(shù)學概念、借助計算技術(shù)可視化數(shù)學概念等手段，以期推動學生對復雜概念的理解與掌握。

關(guān)鍵詞：高等數(shù)學教學；物理類專業(yè)；流體力學

Abstract：Advanced?mathematics?is?an?important?basic?course?for?nonmathematics?majors?in?science?and?engineering，and?it?is?the?first?course?for?other?professional?courses.The?content?of?higher?mathematics?involves?a?wide?range?of?topics，?prominent?key?and?difficult?points，and?the?teaching?difficulty?is?high.The?requirements?of?physics?majors?for?higher?mathematics?courses?are?particularly?significant，which?is?mainly?reflected?in?the?difficulty?of?their?specialized?courses.This?paper?briefly?analyzes?the?physics?professional?course?about?mathematics?using?difficulties，mainly?contains?concepts，abstract?concept，control?equations，etc.，puts?forward?the?corresponding?higher?mathematics?teaching?strategy，mainly?contains?with?the?aid?of?physical?examples?interpretation?of?mathematical?concepts，with?the?aid?of?computational?visualization?of?mathematical?concepts，in?order?to?promote?students'?understanding?and?mastery?of?complex?concepts.

Keywords：higher?mathematics?teaching;physics?major;fluid?mechanics

1?高等數(shù)學的地位、主要內(nèi)容及課程目標

高等數(shù)學是高等學校理工科學生的一門公共基礎課程，往往同線性代數(shù)、概率論與數(shù)理統(tǒng)計等一些課程同時開設。高等數(shù)學作為一門基礎學科，高度抽象、邏輯嚴密、應用廣泛，滲透到所有自然學科，以及部分社會學科中，是推動科技進步的強大動力。馬克思曾說：“一種科學，只有在成功地運用數(shù)學時，才算達到了真正完善的地步。”由此可見高等數(shù)學的地位［1］。

理工科開設的高等數(shù)學偏重實際工程應用，主要研究內(nèi)容包括一元/多元函數(shù)、極限、導數(shù)、積分、常微分方程、向量幾何、曲線積分、曲面積分、多重積分及無窮級數(shù)等相關(guān)知識，內(nèi)容覆蓋廣泛、難度高。

高等數(shù)學開設時間一般為一學年，通過本課程的學習，首先，使學生了解高等數(shù)學所蘊含的一些重要數(shù)學思想，具有運用基本數(shù)學工具進行理論分析，解決實際問題的能力。其次，通過介紹中外數(shù)學名人和數(shù)學典故，激發(fā)學生的人文情懷，燃燒對數(shù)學學習的熱愛。最后，培養(yǎng)學生從多角度思考問題、從事物的正反兩面看待問題的能力。

2?物理類專業(yè)課程對于數(shù)學運用的高要求

物理類專業(yè)課程對高等數(shù)學的要求較高，這主要體現(xiàn)在以下幾個方面。

2.1?概念多

物理類專業(yè)課程難度高，比如電動力學、流體力學、彈性力學、傳熱學等課程，引入了較多的數(shù)學概念，比如梯度、散度、拉普拉斯算子等［2］。舉例來說，一維非穩(wěn)態(tài)熱傳導方程包含了以上三種數(shù)學術(shù)語，對于不可壓縮流體，其方程如下：

其中ρ表示密度，c表示定壓比熱，T表示溫度，t表示時間，表示梯度，q″表示熱流密度，方程（1）對于空間任意一點都成立，其物理意義為：空間某點處單位體積熱能的變化率等于該點熱流密度散度的負數(shù)。熱流密度表示為：

其中k為導熱系數(shù)。對于各向同性材料，k不具有方向性，即各向同性，類似靜止狀態(tài)下，水下某點的壓強，其在任意方向上壓強大小均相等，但對于各向異性材料而言，方程（2）應當變化為：

方程（3）中張量K同T相乘，涉及矩陣乘法，由此可見，物理類專業(yè)課程涉及數(shù)學概念較多，橫跨高等數(shù)學、線性代數(shù)等課程。此外，概率論與數(shù)理統(tǒng)計相關(guān)知識則體現(xiàn)在統(tǒng)計力學等相關(guān)課程之中，這里不再闡述［3］。

2.2?概念的高度抽象性

如前所述，物理類專業(yè)涉及大量數(shù)學概念，比如梯度、散度等。這些概念對于新生而言是高度抽象的，不具體的，比如，梯度代表什么意思？溫度的梯度代表什么含義？梯度同方向?qū)?shù)又有什么關(guān)系？溫度變化最快的方向為什么是溫度梯度的方向？

2.3?控制方程的復雜性

一切物理過程可簡化為若干控制方程，這些控制方程一般表現(xiàn)為偏微分方程，比如表示一維非穩(wěn)態(tài)熱傳導方程、NavierStokes方程、Maxwell方程、Poisson方程等，這些方程很難獲取解析解，給學生理解方程解的特性以及方程背后的物理本質(zhì)帶來了若干困難［4］。

2.4?不同課程間概念的深度融合

普通物理類專業(yè)一般會開設電動力學、流體力學、彈性力學等課程，這些課程中會反復出現(xiàn)相同的概念或知識點。比如電動力學中，若電場可表示為E=-φ，則高斯定律可簡化為：

其中ε表示介電常數(shù)，φ表示電勢，q表示電荷密度，方程（5）本質(zhì)上屬于Poisson方程，這種形式的方程經(jīng)常出現(xiàn)在其他課程中，比如流體力學中帶源項的穩(wěn)態(tài)質(zhì)量守恒方程：

其中φ表示勢函數(shù)，S表示源項。進一步總結(jié)，可得到如下守恒型的物質(zhì)守恒方程，其中J表示有關(guān)ψ的通量，ψs表示源項。

具體來說，ψ=ρ，J=ρu，ψs=0，其中u表示速度，方程（7）簡化為流體力學中的質(zhì)量守恒方程，若ψ=ρcT，J=ρcTu，ψs=0，方程（7）簡化為傳熱學中的能量守恒方程。

3?物理類專業(yè)高等數(shù)學教學的對應策略

針對上述物理類專業(yè)課程的重難點，特提出以下相應教學策略。

3.1?結(jié)合物理背景闡述數(shù)學概念

下面以散度的概念為例，闡述如何結(jié)合物理背景解釋其概念。散度在流體力學和電動力學等物理學科中頻繁出現(xiàn)，下面以流體力學為背景，來分析質(zhì)量通量（ρu）和速度（u）的散度所代表的含義。

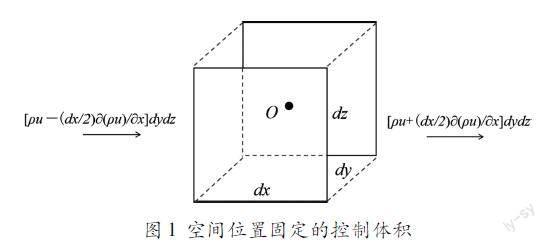
假設流場內(nèi)存在空間位置固定的微小控制體積，其邊界開放，流體可從邊界流出，來計算流出該控制體積的質(zhì)量凈流量，參考坐標系的原點設置在控制體積的幾何中心，如圖1所示。

該點處x方向的質(zhì)量流量為流體密度乘以x方向的速度u。x方向的質(zhì)量凈出流量等于質(zhì)量出流量—質(zhì)量入流量，由于空間位置的變化所引起的質(zhì)量流量增量可以使用泰勒公式近似，同理，可以得到y(tǒng)和z方向的質(zhì)量凈出流量，三者相加就能得到流出整個控制體積的質(zhì)量凈流量，即方程（8）：

m·=ρux+dx2-ρux-dx2dydz+ρvy+dy2-ρvy-dy2dxdz

+ρwz+dz2-ρwz-dz2dxdy（8）

其中v和w分別表示沿y和z軸的速度分量，整理并簡化可以得到：

m·dxdydz=（ρu）x+（ρv）y+（ρw）z=

由此發(fā)現(xiàn)，質(zhì)量通量（ρu）的散度即表示空間某點單位體積質(zhì)量凈出流量。

3.2?突出不同課程之間概念或控制方程相關(guān)性

如前所述，相同的概念會出現(xiàn)在不同的課程之中，比如散度的概念，流體力學中有速度的散度，質(zhì)量通量的散度等，傳熱學中有熱通量的散度等概念，這些物理量的散度有哪些相似之處呢？可以從這些量的單位來分析，速度的散度·u1/sm3/（m3·s），因此，·u的物理含義為空間某點單位體積的體積變化率。質(zhì)量通量的散度·（ρu）kg/（m3·s）表示單位體積的質(zhì)量變化率，若·（ρu）>0，則表示空間某點質(zhì)量凈流出。熱通量的散度·（ρcTu）J/（m3·s）表示單位體積的熱能變化率。由以上三個例子可總結(jié)散度算子的一般規(guī)律，散度一般作用于向量，其物理意義一般可表示為某物理量在空間某點的單位體積變化率，若散度為正，則說明該點處該物理量是凈流出的。

了解了散度的物理意義之后，我們可以將其同守恒方程相聯(lián)系，加強理解。由于散度描述的是空間某點處某物理量的變化率，那么該物理量的守恒方程如何表示？以質(zhì)量通量的散度為例，從量綱一致的角度出發(fā)，必然有kg/（m3·s）kg/（m3·s）這樣一種形式，如果等式右邊用-·（ρu）表示，即該點存在源項，那么等式右端必然表示該點處質(zhì)量的單位體積增加率（凈流入率），單位體積的質(zhì)量即密度，又因為著眼于空間某點，即空間位置固定，所以選擇偏導數(shù)，即ρ/t，整理得到質(zhì)量守恒方程或連續(xù)性方程：

這種推導控制方程的思想可以推廣到其他物理量，比如傳熱學能量守恒方程、NavierStokes方程、Maxwell方程、彈性力學中的位移控制方程等，這些方程都可表示為如方程（7）或方程（10）的通式［5］。

3.3?運用計算機等現(xiàn)代化教學設備輔助闡述數(shù)學概念

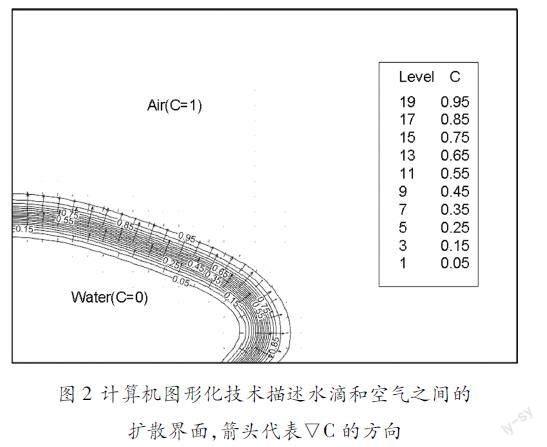
隨著信息技術(shù)的飛速發(fā)展，計算機圖形化技術(shù)也隨之進入科學研究領(lǐng)域，如上所述，梯度的概念是比較抽象的，其可通俗理解為某物理量變化最快的方向，那其為什么是變化最快的方向呢，我們可以結(jié)合圖形化技術(shù)來表征，假設二維平面內(nèi)存在等值線，其方程可表示為C=f（x，y）=y-h（x），C可以取不同值，圖2是運用不同C的值來表示空氣和水液滴之間的界面，此方法稱為相場法，是近些年來流行的界面捕捉方法［6］。

如圖2所示，這些等值線都代表水滴和空氣之間的界面，但是C值的變化是有規(guī)律的，其在界面附近快速變化，但當接近某一相（空氣或水滴時），其值趨近于一個固定值。箭頭代表C的方向，即變化最快的方向，其主要集中在界面附近，在相主體區(qū)域內(nèi)，其幾乎為零。

結(jié)語

本文針對物理類專業(yè)高等數(shù)學教學，簡要回顧了物理類專業(yè)課程存在的重難點數(shù)學概念，提出了相應的高等數(shù)學教學策略。

（1）結(jié)合物理背景闡述數(shù)學概念，使得高等數(shù)學的講授不再是枯燥的，而是生動的、活潑的，富有生命力的。

（2）打通不同概念之間的相關(guān)性，物理學中不同專業(yè)課程之間的一些概念是相通的，因此在教學中可適當總結(jié)這些概念之間的規(guī)律性，以方便學生理解、觸類旁通、舉一反三。

（3）運用現(xiàn)代化教學設備輔助闡釋數(shù)學概念。隨著計算機技術(shù)的蓬勃發(fā)展，給高等教育的教學帶來了深刻的變化，使數(shù)學概念圖形化、可視化應該得到足夠重視。

參考文獻：

［1］李蓉，何振華，胡小春.高等數(shù)學教學現(xiàn)狀的分析與思考［J］.高教學刊，2022，8（04）：8083+88.

［2］王喜鵬，張慶臣，毛偉建.基于上下行波分解的分數(shù)階拉普拉斯算子黏滯聲波逆時偏移成像方法［J］.石油地球物理勘探，2023，58（04）：872882.

［3］王文寧.經(jīng)典統(tǒng)計力學中的正則分布及系綜理論［J］.復旦學報（自然科學版），2023，62（01）：18.

［4］趙春芳.基于研究型教學的偏微分方程實例剖析［J］.高教學刊，2019（26）：106108.

［5］黃忠文，張博文，唐明哲，等.彈性力學與流體力學基本方程的統(tǒng)一性［J］.力學與實踐，2022，44（03）：672676.

［6］王小雙，張良奇，肖姚，等.紅黑著色的相場兩相流并行投影算法［J/OL］.重慶大學學報：112［20230910］.http：//kns.cnki.net/kcms/detail/50.1044.N.20230704.1538.002.html.

作者簡介：沈明廣（1988—?），男，漢族，江蘇建湖人，博士研究生，講師，研究方向：計算流體力學。