地鐵線路高峰大客流協調控制研究

吳開信 鄭怡歡 易佳 鄭陽飛 龍應圖

摘?要：針對地鐵網絡化運營中客流時空不匹配造成的周期性擁擠問題，提出高峰期地鐵線路客流協調控制策略。先對地鐵客流需求特征進行分析，考慮行車條件、站臺承載率要求等，基于安全前提下以提高運營效率為目標，構建地鐵線路客流協調控制的多目標整數規劃模型，并設計遺傳算法進行求解。算例表明了模型的可行性和算法的有效性。

關鍵詞：地鐵；客流協調控制；多目標整數規劃；遺傳算法

隨著城市化水平不斷提高，城市內部的客流需求激增，地鐵在短距離輸送中起到關鍵性作用，但需求的激增卻給地鐵運輸能力帶來挑戰，早晚高峰時段時常出現客流擁擠的狀況。地鐵更是承擔著運送乘客與保障運營安全的任務。針對城市軌道交通客流產生的影響，相關學者研究有吳冰芝［1］基于高峰時段大客流的傳播和影響，提出相關的運營組織方案；李冰玉等［2］分析了路網中大客流擁擠傳播規律，建立基于動態客流的擁堵傳播模型并提出相應的預防措施。蔣熙等［3］基于大客流網絡背景，考慮對路網客流的分布進行仿真建模，并以北京地鐵為實例進行驗證。

而針對客流控制方面，研究內容主要集中在降低運營風險、提出客流方案、提高旅客周轉量等。在降低運營風險方面，石俊剛等［4］考慮客流聚集預警值最小化的目標，構建安全導向下地鐵多車站客流協同控制單目標模型；Yuan等［5］綜合考慮客流需求與列車運輸能力等關系，建立路網級的客流協調控制模型，以確保高峰時段列車運行安全。在提出客流組織方案方面，劉金博［6］通過對上海市各地鐵站客流管控組織方式的調查，對已有導流和限流的設施形式、合理性進行分析，針對行人流線和限流設施提出對應的優化建議。在提高旅客周轉量方面，魯工圓等［7］針對客流需求大于運輸能力供給的地鐵線路問題，基于客流—運行圖網絡以旅客周轉量最大為目標，建立地鐵客流控制的整數線性規劃模型。

現有客流研究對于客流集聚風險考慮較少，本文以各車站控流率及乘客出行延誤時間最小為優化目標，建立多站點協調控制的整數規劃模型，并基于遺傳算法改進方法進行求解。最終以廣州地鐵5號線為例，驗證模型和算法的有效性。

1?地鐵高峰期客流協調控制建模

現階段地鐵面臨的大客流為工作日的高峰期周期性擁擠，根源在于線路運輸能力與客流需求之間的時空不匹配。乘客短時間內過多涌入某一車站造成其負荷過大，車站無法承擔溢出客流的運營，可能產生客流擁擠。

為便于建模，現對客流控制時間進行劃分。對連續時間范圍T離散化，T=1，2，…，t，…，T，其中t為具體的客流控制時段，K則為車站集合，K=1，2，…，k，…K。

1.1?模型假設

（1）工作日高峰期客流需求穩定，波動性較小；

（2）高峰時段客流到達比較穩定，以每15min劃分客流時段；

（3）客流控制時段內，列車停靠站臺時下車乘客會快速出站。

1.2?客流需求與線路輸送能力約束

以Qac（k，t）為第t個客流控制時段車站k的實際客流需求量，Qa（k，t）為第t個控流時段車站k的新到達客流量，則當t=1時，新到達客流量等于實際客流量有：

Qac（k，t）=Qa（k，t），t=1（1）

以Qs（k，t）為第t個控流時段在車站k站臺處的滯留乘客數，Qin（k，t）為第t個控流時段車站k的最佳上車乘客數，則其余時段實際客流量為前一時段客流控制后的滯留客流量及新到達客流量之和，有：

Qac（k，t+1）=Qa（k，t+1）+Qs（k，t），t∈T，k∈K（2）

Qs（k，t+1）=Qac（k，t）-Qin（k，t），t∈T，k∈K（3）

客流控制是為了減輕運營組織壓力，最大限度地滿足乘客的出行需求。既不能超過實際客流需求，也需滿足乘客最低需求。

Qin（k，t）

Qac（k，t），t∈T，k∈K（4）

Qin（k，t）ηQac（k，t），t∈T，k∈K（5）

線路輸送能力Cmax是指在設施設備及行車組織方法一定下，單位時間所能運送的乘客數。公式如下：

Cmax=nmax·m·P（6）

nmax——單位時間內通過的最大列車數；

m——列車編組輛數；

P——每輛車的定員數。

在地鐵運營過程中，若線路某區間的通過客流量超出其最大輸送能力，可能導致區間擁擠，乘客在車站站臺上滯留，以Q（l，l+1，t）為第t個控流時段線路經過l至l+1的斷面客流量，則有：

Q（l，l+1，t）

Cmax·Φ，t∈T（7）

為避免發生乘客大規模集聚，對客流斷面區段的列車滿載率進行約束為：

以σ（k，l，l+1，t）為第t個控流時段車站k上車通過l至l+1斷面的客流通過率，以q（k，l，l+1，t）為第t個控流時段經車站k上車通過l至l+1的斷面客流量，具體如式（9）～（10）：

σ（k，l，l+1，t）=q（k，l，l+1，t）Qac（k，t），l1，t∈T，k∈K（9）

Q（l，l+1，t）=∑mi=1Qin（k，t）σ（k，l，l+1，t），l1，t∈T，k∈K（10）

1.3?目標函數

當地鐵運力無法滿足客流需求時，會導致乘客出行延誤時間增加，乘客滿意度降低。而當大量乘客在車站站臺處集聚，就會使得部分乘客因列車運力不足而滯留，出于車站運營和乘車公平性考慮，且確保站臺乘客集聚的安全，本文設置的雙目標為：第t個控流時段車站的控流率v（k，t）和乘客出行延誤時間最小。因此目標函數f為：

f=f1+f2（11）

f1=min（max（v（k，t）））（12）

f2=min∑Tt∑KkQs（k，t）·f（13）

v（k，t）=Qs（k，t）Qac（k，t）（14）

1.4?算法設計

本文研究的地鐵高峰時段線路多站點協調優化模型比較復雜，變量較多，因此采用智能優化算法求解。而遺傳算法是基于生物種群進化行為的高效全局搜索的優化算法，利用其特殊算子可解決許多復雜的問題，因此基于遺傳算法進行模型求解過程如下：

（1）確定決策變量集、目標函數，線路中控流車站共K個，高峰期控流時段共分為T個，決策變量為各控流時段內各車站的上車客流量，一共有KT個。

（2）確定編碼方案。設計n維實數編碼（n是車站數）表示各個站點上車客流量。

（3）適應度函數。由于模型目標函數包含各站點控流率與乘客出行時間延誤兩部分，需將多目標函數轉換為單目標函數。歸一化處理后，在迭代中根據所累計的最優及最差可行解。記錄當前迭代次數q（q>1），在第q-1代搜索到最優可行解的目標函數值為y1b與y2b，而最差解的目標函數值為y1w與y2w，當前解Xkq的目標函數值即為y1k與y2k，則總適應度函數為：

fj=α1y1w-y1ky1w-y1b+α2y2w-y2ky2w-y2b（15）

其中α1、α2為權重系數，取值為［0，1］，代表目標函數所占重要程度。記錄最優函數值z1j與最差函數值z2j，則總目標最優值為：

zj=α1z1j+α2z2j（16）

（4）選擇。由個體適應度值計算被選中的概率Pjs，選擇優秀個體形成下一代，假設個體j的適應度是Fj，則個體j被選中的概率是：

Pjs=Fj/∑mj=1Fj（17）

（5）交叉。按照交叉概率Pc交換父代的部分基因得到新個體，假定在個體XqC和XqD之間進行交叉操作，d為交叉系數，取值范圍為［0，1］，則新個體為：

Xq+1C=dXqD+（1-d）XqC

Xq+1D=dXqC+（1-d）XqD（18）

（6）變異。按照變異概率Pv得到新個體。

（7）判斷。遺傳算法是通過隨機搜索產生結果，其求得的解并非全部滿足條件，需通過模型的約束條件來判定可行解，如若不滿足則需不斷重復3～6的操作，直至滿足停止準則為止并輸出結果。

2?算例驗證

本文以廣州地鐵5號線為具體算例，對線路各個時段客流量進行分析處理，結合高峰期客流分布特點計算各站點最優上車客流量，制訂準確有效的控流方案。

廣州地鐵5號線全長31.9千米，共設置24座車站，列車采用6節編組L型列車，將工作日晚高峰（17：00—19：00）進行分段。

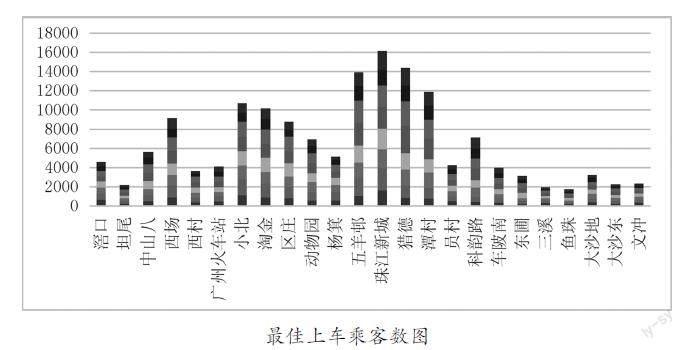
對上述模型求解，得到各時段各站點最優上車客流量Qin（k，t）如下圖，可得：5號線客流量在潭村站出現分界，該站點后進站人數較前半段明顯減少，線路前半段中間站點的客流量最大，由于潭村為換乘站，高峰期其換乘比例較大。得到各站點滯留乘客數，可知部分站點滯留數極小，幾乎沒有乘客在站臺滯留，說明客流控制模型是科學有效的。

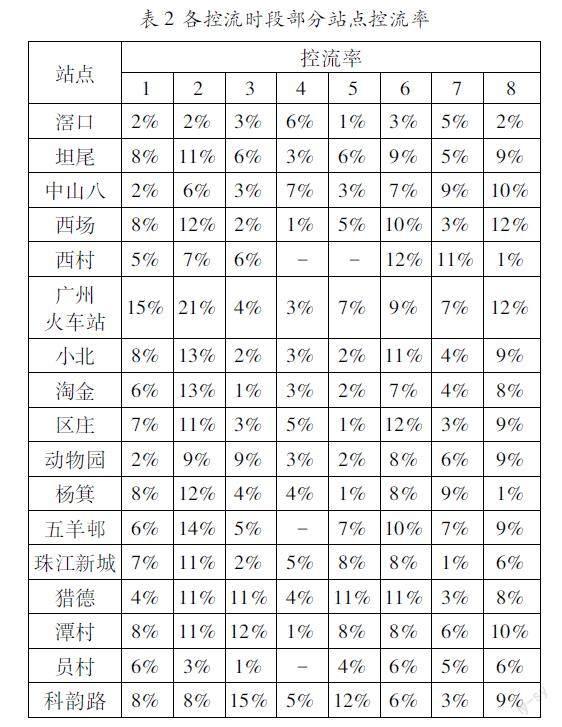
模型求解得各站點最大控流率為f1=0.21，即每個控流時段最多只有21%的乘客滯留。如表2時段3～5的控流率較小，是因為該時段線路上大多數列車開始到站發車，而時段2的控流率最高，是由于該時段集聚了大量候車的乘客，且在線路前半段站點的擁擠度最高，與模型計算結果在第2時段前幾個站點控流率最大保持一致，為后面站點的疏通提供保障。模型結果符合晚高峰客流分布情況，滿足協調控制目標，具有可實踐性。

以乘客延誤時長為評價指標，得出控流策略的有效性，協調控制后的站點比未協調的站點延誤時間減少了79337人·min。通過對線路上游車站進行控流，使得列車駛向下游車站時剩余運力較多，站臺滯留乘客減少，延誤時間也明顯降低。

結語

本文提出了常態化運營下地鐵高峰時段客流協調控制模型，該模型以各站點的最優上車乘客數為決策變量，求得各車站的滯留乘客數，以此確定各車站的控流率，進而能最大化滿足乘客的出行需求。通過實例分析已證明其有效性，該模型也可應用于常態化大客流車站的管控等情況。

參考文獻：

［1］吳冰芝.城市軌道交通高峰時段大客流擁擠傳播研究［J］.科技與創新，2016（07）：3334.

［2］李冰玉，秦孝敏.城市軌道交通網絡大客流擁堵傳播機理研究［J］.中國安全科學學報，2016，26（01）：162168.

［3］蔣熙，馮佳平，賈飛凡，等.大規模城軌路網客流分布推演的建模與仿真方法［J］.鐵道學報，2018，40（11）：918.

［4］石俊剛，楊靜，楊立興.以安全為導向的地鐵高峰時段多車站客流協同控制模型［J］.交通運輸系統工程與信息，2019，19（1）：125131.

［5］YUAN?Fuya，SUN?Huijun，Kang?Liujiang，et?al.Passenger?flow?control?strategies?for?urban?rail?transit?networks［J］.Applied?Mathematical?Modelling，2020，82（C）.

［6］劉金博.上海市軌道交通車站客流控制方法及問題研究［J］.交通世界，2020（27）：34.

［7］魯工圓，馬駟，王坤，等.城市軌道交通線路客流控制整數規劃模型［J］.西南交通大學學報，2017，52（02）：319325.

基金項目：江門市基礎與理論科學研究類科技計劃項目（項目名稱：地鐵線路高峰期列車時刻表調整和限流協同優化研究，編號：2022JC01002）；五邑大學大學生創新創業訓練計劃項目（項目名稱：地鐵線路高峰大客流協調控制研究，編號：202211349233）

作者簡介：吳開信（1972—?），男，漢族，安徽肥東人，講師，研究方向：交通運輸。