SAR無線電引信目標定向探測模型及仿真

張恒瑞,景 華,李楚寶,2,付勝華,牛蘭杰,2,楊金鋼,2

(1.西安機電信息技術研究所,陜西 西安 710065;2.機電動態控制重點實驗室,陜西 西安 710065)

0 引言

引信定向探測與戰斗部破片飛散角控制相結合,可實現精確控制戰斗部起爆時間、彈目交會距離、方位角,使得戰斗部爆炸破片指向目標,可以增加戰斗部的殺傷威力[1]。激光、紅外以及無線電探測引信是當前引戰配合定距/定向起爆控制的主流方式[2-3],但激光、紅外易受到煙霧等自然環境干擾而產生誤作用。如何有效提高無線電引信定向精度,對提高引戰配合毀傷具有重要意義。

合成孔徑雷達(SAR)通過雷達運動形成大口徑天線,從而獲得具備方位向的高分辨率目標圖像[1]。將SAR技術應用于無線電引信的精確目標識別與定位起爆控制,相比光學、紅外引信具有全天候、全天時、抗干擾強的優點[2-3],是解決彈載高速環境下無線電引信定向起爆控制的重要技術途徑。相關學者研究了機載雷達、彈載雷達導引的SAR目標成像定位追蹤技術[4-7],如德國的MMW-SAR對地導彈、美國的LRASM反艦導彈等都已應用SAR技術,展現了其高精度的打擊能力[8]。然而,常規彈藥的雷達導引頭通常存在近距盲區[9],目標的位置無法觀測,因此研究SAR引信目標識別與定位技術具有現實意義。

基于SAR的定向定距探測引信的關鍵技術在于獲取彈體與目標的方向角。文獻[10—12]提出的三點線性約束自適應單脈沖測角是目前雷達中應用較廣的方位角測量方法。在此基礎上,文獻[6]通過增加差波束副瓣約束的方法降低副瓣電平,維持線性單脈沖比斜率,提出了一種低副瓣自適應單脈沖測角方法。文獻[7]通過約束條件對二維方向信息去耦合,采用廣義單脈沖測角技術進行角度估計,建立了平面陣約束自適應單脈沖測角算法。但上述算法均基于機載水平面測角,對于彈載高落速大斜視落角還未開展研究。本文針對導引近距盲區彈體與目標交會段高速大斜視環境,提出了一種基于SAR的彈載無線電引信目標定向模型。

1 SAR無線電引信原理

SAR的基本原理是以小尺寸雷達的運動得到一個較長的合成孔徑,進而獲得與之成反比的極窄波束[13]。如圖1所示,在俯沖前斜式彈目交會段,彈體無姿態變化且其偏航角、俯仰角、橫滾角為0,以落角α、勻速v運動,并假設無線電引信實際的天線孔徑以脈沖發射的電磁波束主瓣與彈軸的夾角(定義為主瓣前傾角)與合成孔徑波束主瓣前傾角相等。

圖1 無線電引信SAR原理示意圖Fig.1 Schematic diagram of the radio fuse SAR principle

以線性調頻(LFM)引信為例,信號時域表達式為

(1)

(2)

對應脈沖的LFM回波信號可以表示為

sn(t)=σ·?(t)·s0[t-2R(t)/c],

(3)

式中:?(t)為天線方向圖增益。對N個脈沖回波信號進行每一步信號的求和,可以表示為

s(t)=∑nσ·?(t)·p[t-nTr-2R(t)/c],

(4)

式中:?(t)為天線方向圖增益,R(t)為目標與引信之間的距離,Tr為脈沖間隔時間,c為光速。

通過匹配濾波器對回波信號進行脈沖壓縮。設濾波器的傳輸函數為H(w),為了滿足最大信噪比,有

H(w)=KF*e-jwt0,

(5)

式中:F*為傅里葉變換的共軛,t0是濾波器件的時間延遲,K為增益常數。則回波信號s(t)通過濾波器,經過卷積運算處理后得到的信號s1(t)表達式為

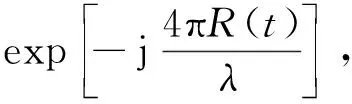
(6)

式中:δR為脈沖距離向壓縮后的沖擊函數。

將脈沖內的時間變化稱為快時間,脈沖間的時間變化稱為慢時間,其發射頻率稱為脈沖重復頻率(PRF)。文獻[14]在合成處理過程中,將每一步的回波信號按照快、慢時間重新排列為二維陣列,第n列表示第n個脈沖對應的回波,那么合成后的完整回波信號表達式可以被重寫為

(7)

式中:τ=t-nTr。

2 目標定向模型設計

目標定向的關鍵在于獲取彈體與目標的方向角。采用脈沖和差信號比幅法進行目標與彈軸交角的計算。首先,針對地面目標彈目交會的特殊環境,建立如圖2所示模型。設計兩束相同且相交的波束,其中,定義波束2的主瓣前傾角為θ1,波束1的主瓣前傾角為θ2,θ0為波束交點處與彈軸的夾角,其值通常為半功率波束寬度的一半,θ為合成孔徑處目標與彈軸的夾角,β為實口徑處目標與彈軸的夾角,即所求方位角。

圖2 目標方位角計算原理示意圖Fig.2 Schematic diagram of the principle of calculating the target azimuth

隨后進行算法設計。定義和差波束角θk:

θ1-θ0=θ0-θ2=θk。

(9)

假設天線幅度增益方向性函數為F,可以得到兩個接收天線的幅度增益方向性函數為

F1(θ)=F(θ-θ0+θk),
F2(θ)=F(θ-θ0-θk)。

(10)

令θt=θ-θ0,則波束1收到的回波信號為

u1=KF1(θ)=KF1(θt+θk),

(11)

波束2的回波信號為

u2=KF2(θ)=KF2(θt-θk),

(12)

式中,K為增益系數。得到兩個波束的回波信號的幅度后,再進行比值運算,得到兩個接收天線的信號幅度比為

(13)

將信號從天線的輸出端加到和差變換器進行信號的求和與做差運算,得到和信號與差信號為

FΣ(θ)=F1(θ)+F2(θ),
FΔ(θ)=F1(θ)-F2(θ)。

(14)

接收的兩個和波信號振幅不同而相位相同,在和差比較器的兩個輸入端口分別輸入接收機收到的具有相同相位的目標回波信號,可以得到

EΣ=FΣ(θ)*FΣ,(θ),
EΔ=FΣ(θ)*FΔ(θ)。

(15)

對和差信號做比值:

(16)

即可以通過和差波束的輸出比FΔ/FΣ算得唯一變量θ的值。

根據模型中幾何關系可得

(17)

式中:d為合成天線孔徑半徑,R為天線中心距目標的距離,Rn為彈體距目標的距離。d與R為已知量,即可解得目標相對于彈體方位角β。

3 仿真計算及定向精度影響因素分析

3.1 回波信號仿真及測角精度驗證

根據上述建立的目標定向模型可知,目標的定向精度與回波信號和差運算后的幅值,即SAR合成能力與和差波束的角度相關。初步分析可知窄波束相對有更好的幅值分辨力,即定向精度更好[15]。結合引信在實際應用中的參數進行仿真分析,不考慮彈體的姿態角,設定仿真基本參數如表1所示。

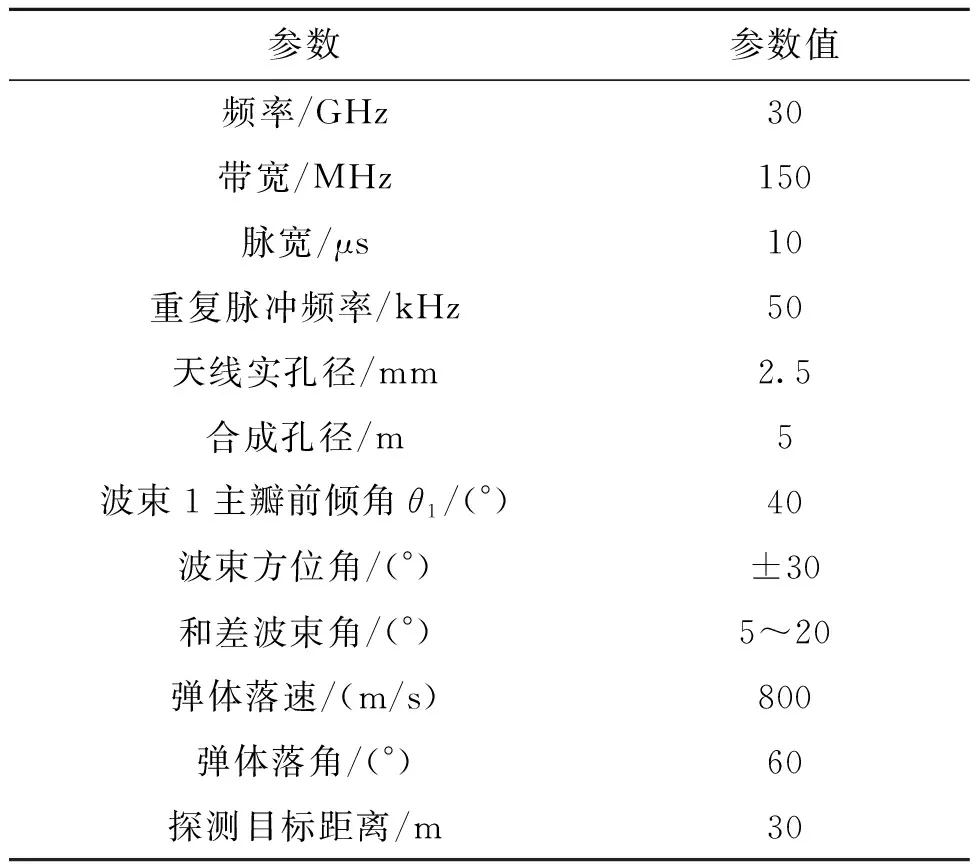
表1 仿真基本參數表Tab.1 Static rain field simulation test device

表1參數中,波束前傾角、彈體落角與落速決定了SAR的合成能力,彈體落速決定了回波信號脈沖壓縮的信噪比,即方位相的分辨率[16],對此本文不做重點討論,θ1取值為30°,彈體落角為60°,彈體落速為800 m/s。LFM信號頻譜圖及目標回波信號如圖3、圖4所示,可以看到,目標的回波信號經過SAR合成后明顯提高了信噪比。

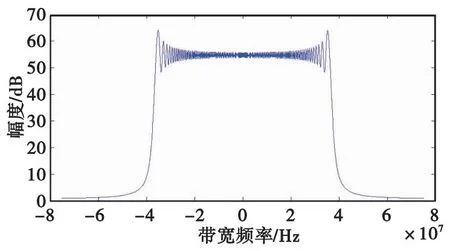
圖3 LFM頻譜圖Fig.3 LFM spectrogram

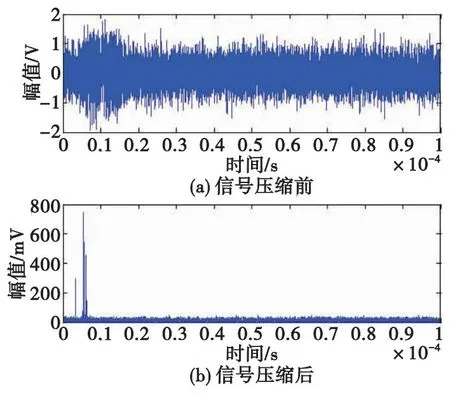
圖4 LFM回波信號圖Fig.4 LFM echo signal diagram

根據表1中的仿真參數,取波束2的主瓣前傾角θ2為42°,兩波束的交點與主瓣相位中心的夾角θk取值為2°,得到目標在合成孔徑與彈軸的夾角θ絕對值,如圖5所示。

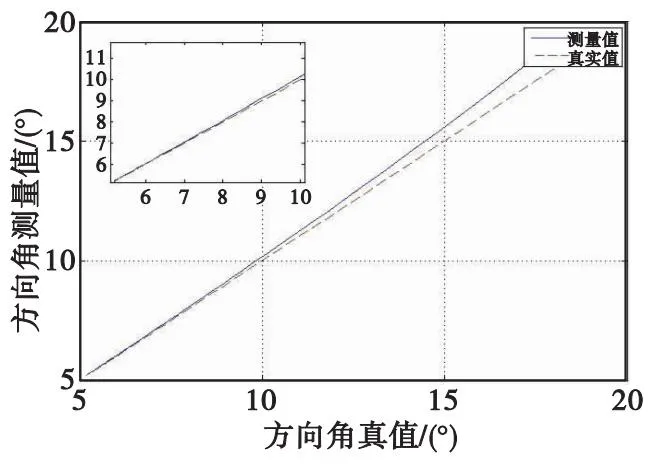
圖5 方向角真值與測量值對照圖Fig.5 Directional angle truth vs. measured value

可以看到測量值和真值在5°～20°有較好的擬合度,誤差小于1.2°。兩個夾角越小,測量精度越高。在目標距離R為30 m,合成孔徑為5 m的確定參數下,通過式(17)可以得到目標與彈體實孔徑的測量角度范圍為39°～64°。

為了進一步驗證合成孔徑的優點,對不采用SAR合成的目標方向角仿真,如圖6所示。

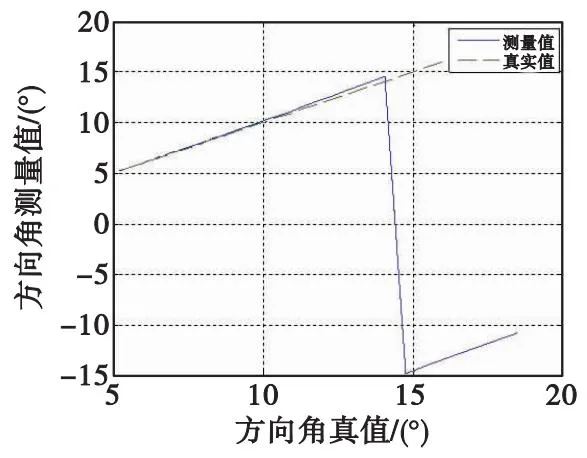
圖6 未采用SAR時方向角真值與測量值對照圖Fig.6 Directional angle true vs. measured plot when SAR is not used

顯然在未采用SAR合成測量時,方向角測量值在接近15°時出現巨大誤差,無法完成測量任務。這是因為在未采用SAR的情況下,安置的天線需要采用較大的真實孔徑,從而使得兩陣元的間距增大,有效測量范圍降低。因此采用SAR技術能夠提高測量范圍和測量精度,提高適用性。

3.2 合成孔徑大小對測角精度影響分析

對Ka波段實際孔徑與合成孔徑得到的波束方向圖如圖7所示。可以看到在保持發射波各項參數不變的情況下,采用SAR技術后,等效天線孔徑更大,方向圖收縮更明顯,對目標的回波信號能量更集中,根據式(9)—式(16)的和差測角理論,可以得到的測角精度越高。

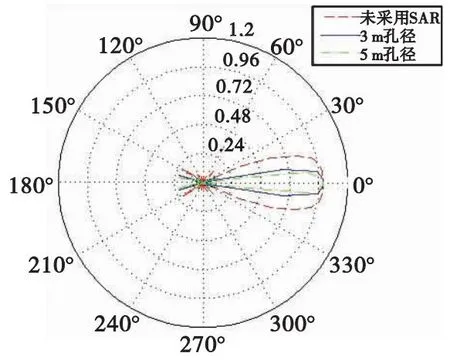
圖7 不同合成孔徑下波束方向圖對照圖Fig.7 Comparison diagram of antenna pattern under different synthetic apertures

然而,方向圖的收縮帶來波束掃描區域變窄,易丟失目標,對目標的方位角探測區域需要結合引戰配合另作重點討論。

3.3 和差波束角θk對定位精度影響分析

保持其余仿真參數不變,取波束1和波束2的交點與主瓣相位中心的夾角θk分別為2°,4°,6°,8°,驗證測角誤差結果如圖8所示。

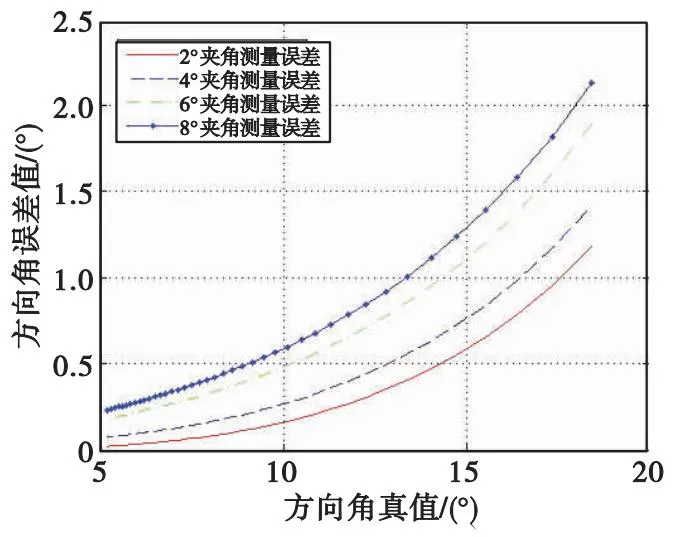
圖8 不同夾角下測量誤差對照圖Fig.8 Comparison chart of measurement error at different angles

從圖8可以看到θk越大,測角誤差越大,原因是當θk增加時,兩個波束相交的部分減少,所生成和差信號的適用空間減少,測量誤差增大。在極端情況下,當夾角超過天線主瓣寬度,使得兩個波束完全不相交時,算法工作無法完成。因此在設計天線安裝時,應當控制兩個天線夾角在4°～6°。

3.4 彈目交會距離影響分析

保持其余仿真參數不變,取天線中心距目標的距離R為10～30 m,驗證測角誤差結果如圖9所示。

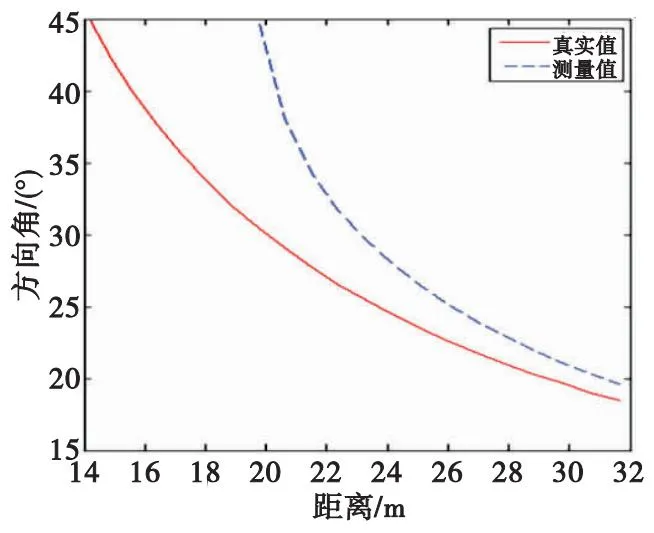
圖9 彈目距離與測量誤差關系圖Fig.9 Relationship between projectile distance and measurement error

從圖9可以看到彈目距離越遠,測量誤差值越低,原因是彈目距離越遠,兩個波束的回波信號區別越大,形成的和差信號越清晰,有利于提高測角精度。但在實際應用中,應當考慮戰斗部起爆時對彈目距離的要求,以及考慮探測距離能力的限制。彈目距離在22～32 m時,測量角度誤差值不大于3.4°。

4 結論

本文建立了一種基于SAR的脈沖測角算法。該方法基于SAR的合成原理,通過構建面向地面目標的彈目交會場景,對SAR合成回波信號進行和差計算,得到了目標與彈軸的夾角,應用于彈載俯沖的無線電引信對目標的方位角測量。驗證結果顯示,該算法相比未采用SAR的測角方法,能夠提高測量方位的范圍,在引信參數條件下,對39°～64°的目標方向識別誤差不大于1.2°。算法得到了SAR合成孔徑大小、目標方位角和彈目距離對定向精度的影響規律,表明了該算法的可行與泛用性,在對地引信目標定向領域具備一定的應用價值。