中大口徑加榴炮發射環境極限邊界工況炮彈引耦合響應特性

田中旺,牛蘭杰,寧變芳,馬紅萍,孫誠誠

(1. 機電動態控制重點實驗室,陜西 西安 710065;2. 西北機電工程研究所,陜西 咸陽 712099)

0 引言

中大口徑加榴炮機械觸發引信[1-3]是中大口徑殺傷爆破榴彈的主要配用引信,裝配數量巨大,在產品交驗、部隊演訓等過程中多次出現彈道炸問題,且歷經多輪次的改進設計,彈道炸問題仍未解決[4],其主要原因與中大口徑加榴炮高動態發射環境條件下引信響應特性不清晰、失效機理不明確有關。

配用機械觸發引信的中大口徑殺傷爆破榴彈在火炮發射過程中承受的高動態環境激勵主要由發射藥燃燒膛壓推動彈丸運動過程產生的后坐沖擊過載、彈帶擠進阻力、彈丸旋轉離心過載、彈丸與身管橫向撞擊力以及出炮口瞬間彈丸軸向、徑向約束狀態突變導致的振蕩沖擊過載等耦合構成,其激勵水平主要受火炮身管磨損程度、彈丸形態、發射裝藥量、彈引連接軸線偏離程度等火炮、彈丸、引信的技術狀態影響[5-6]。其中,現役中大口徑殺傷爆破榴彈彈丸形態主要分為平底彈、底凹彈和底排彈。底凹彈是通過在彈丸底部設置凹陷空腔實現減少阻力增加射程的炮彈。底排彈是通過在彈丸底部設置燃氣裝置,利用其發射后燃燒產生燃氣平衡彈頭、彈尾壓力差,實現減少阻力并大幅增加射程的炮彈;底排彈發射過程中火藥燃燒產生的膛壓顯著大于底凹彈[7-8]。發射環境中大口徑機械觸發引信極限邊界工況是綜合考慮上述影響因素的邊界狀態,是引信高動態環境響應特性和失效機理分析的重要邊界條件。

近些年,國內眾多科研人員針對中大口徑火炮、彈丸、引信的響應特性開展了研究。文獻[9]構建了中大口徑加榴炮身管與榴彈耦合非線性動力學響應模型,仿真分析了內彈道階段彈丸擠進過程與身管的碰撞特性,研究了身管彎曲程度、彈軸偏心情況等因素對碰撞特性的影響。文獻[10]構建了身管-彈丸耦合非線性有限元彈塑性模型,分析了彈丸裝填情況、裝填角狀況、摩擦狀態、彈炮配合間隙等因素對耦合系統動態響應特性的影響。文獻[11]構建了底排彈動態響應模型,通過模態和動力學仿真分析了彈丸固有頻率及關鍵部位響應特性,并對底排彈發射安全穩定性進行了判斷。文獻[12]針對國內某底排彈在部隊訓練時出現引信彈道早炸故障,對該底排彈的生產狀態及試驗過程進行了分析與驗證,并通過理論計算,獲得引起引信彈道早炸的主要原因可能是小射角裝填底排彈不到位。文獻[13]主要針對火炮發射裝藥量、彈丸與火炮身管的配合間隙、彈丸裝填到位情況以及火炮身管的磨損情況等底凹彈平臺下的獨立工況開展了引信典型部位的響應特性和失效分析。文獻[14]建立了彈丸與火炮內彈道耦合作用過程動力學響應模型和彈引多剛柔體動力學響應模型,結合隨機統計算法分析了引信在彈丸內彈道發射階段的動態響應特性。上述研究或者從炮彈耦合層面分析了彈炮響應特性,或者以引信及其典型機構在典型工況下的響應特性作為研究重點,對綜合考慮火炮身管狀態、彈丸形態、彈引連接狀態等邊界條件的炮-彈-引耦合分析較少,難以高保真地反映引信高動態環境動態響應特性,支撐引信內、外彈道失效機理分析和環境適應性設計。

本文通過建立考慮火炮身管中后期磨損、彈丸形態、彈-引軸線極限偏離等因素的炮-彈-引耦合多級多體動力學彈塑性仿真模型,采用有限元仿真結合試驗驗證的方式,從內彈道和出炮口階段彈丸擠進阻力、橫向撞擊力、姿態角以及引信典型機構過載等參量分布特征,分析發射環境極限工況彈-引典型機構響應特性,為中大口徑加榴炮機械觸發引信內、外彈道失效機理分析提供支撐。

1 SPH和Lagrange有限元融合算法

國內外關于彈丸膛內運動的分析,大多采用有限元法,理論成熟、計算效率高、數值精度也較高。但是,有限元法是基于網格的數值方法,常規有限元方法(Lagrange)在分析彈帶擠進過程大變形時,會出現嚴重的網格畸變現象,給求解帶來很大困難。本文在常規有限元分析方法的基礎上,對彈丸在擠進過程中發生大變形的彈帶部分采用光滑粒子法(SPH)[15-16]建模;對于身管、彈體和引信等變形較小的區域,則采用Lagrange有限元法建模。

SPH法是一種求解偏微分方程的數值方法,屬于無網格法的一種。其核心步驟是:對場函數采用積分近似表示法的核近似過程;對積分近似方程進行離散化的粒子近似過程。

對于任意函數f(x),x為位置矢量,它在解域Ω中可以表示成如下積分形式:

(1)

用函數ω(x-x′,h)來代替式(1)中的δ函數,用f(x)的梯度?f(x)代替f(x),該函數空間導數的核估計表達式為

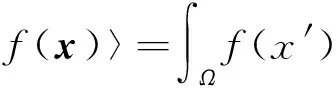
(2)

光滑粒子近似過程中,將整個解域離散成一系列任意分布的粒子,物理量的計算只在粒子上進行,因此核估計的積分表達式可轉化為粒子求和的離散化形式。假定解域Ω被離散成N個帶質量的粒子,粒子j的位置矢量為xj,粒子的體積為ΔVj,粒子的質量為mj,粒子的密度為ρj。因此,在粒子i處的函數值f(xj)的SPH粒子近似式為

(3)

函數f(x)導數的積分表達式(2)可轉化為離散化的粒子近似式:

(4)

在固連接觸中,SPH粒子定義為從節點,將與SPH粒子接觸界面的實體單位表面定義為主表面。如果從節點與對應的主段間有微小的距離存在,則采用正交投影的方法將從節點移動到主表面上。SPH粒子固連在Lagrange單元上的示意圖如圖1所示。

圖1 SPH粒子被固連在Lagrange單元上示意圖Fig.1 Diagrams of SPH particles being fixedly attached to Lagrange units

固連接觸物理量仿真求解過程[17]:對非接觸表面的 SPH 粒子及Lagrange單元,從接觸表面上節點的已知速度、位移開始,由Lagrange單元的物理量計算相應單元應力、應變率等;由SPH粒子的物理量計算SPH粒子應力、應變率等;在此基礎上確定每個 Lagrange單元節點的力、SPH粒子及粒子周圍臨近節點所受的力;再計算下一時刻所有節點的速度、位移;循環直至完成整個求解時間內的計算。

2.1 有限元模型

以中大口徑加榴炮身管、彈丸、機械觸發引信、簡化后的安全系統結構模型為主體,構建炮-彈-引典型機構耦合動力學仿真模型,如圖2所示。

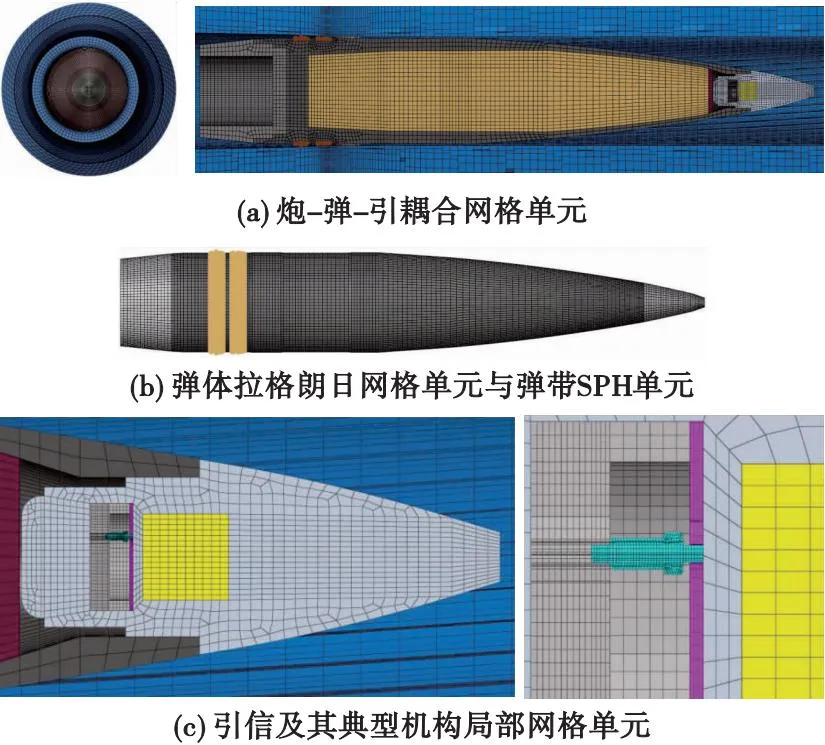
圖2 炮-彈-引耦合仿真模型Fig.2 Rifled gun barrel-projectile-fuze coupling simulation model

圖2中,身管模型為大口徑加榴炮身管混合深膛線模型,彈丸模型分為底凹彈和底排彈模型,引信簡化模型由引信體、安全系統、延期裝置配重等構成,安全系統模型主要由回轉體軸和上、下夾板等構成,榴彈和引信模型均未考慮螺紋連接狀態。彈帶采用SPH方法建模,固連處理中將彈帶 SPH 粒子定義為從節點,將與 SPH 粒子接觸界面上的彈體單元表面定義為主表面。

仿真計算主要材料參數如表1所示。

表1 主要材料參數Tab.1 Main material parameters

其中,彈帶采用塑性隨動強化模型,材料本構關系模型為

(4)

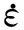
2.2 仿真邊界條件設置

約束身管后導向段與搖架后銅襯支撐位置三個方向自由度,約束身管前導向段與搖架前襯套接觸位置垂直方向自由度。載荷分別為大口徑殺爆彈底凹彈、底排彈0號裝藥彈底壓力設計參數,施加到彈底的載荷曲線如圖3所示 。

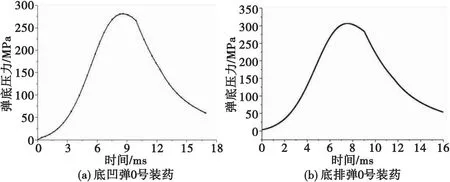
圖3 彈底壓力曲線Fig.3 Bottom pressure curve

2.3 仿真工況條件

仿真計算包括重力作用下身管靜撓度、彈丸在初始裝填速度作用下卡膛過程、彈丸在膛內壓力作用下彈炮耦合作用過程等計算步驟。本文主要以彈丸在膛內壓力作用下彈炮耦合作用過程為主,對炮-彈-引耦合響應特性進行分析。仿真計算工況主要包括3種,如表2所示。以中大口徑加榴炮身管實際使用壽命、底排彈常規發射最大裝藥量、彈引加工導致的極限偏差,作為極限邊界條件的設置依據。極限工況對應的技術狀態為:身管中后期磨損、底排彈、0號裝藥、彈炮間隙2.65 mm、初始裝填角0.5°、彈引極限軸線偏差≥0.7 mm、角度極限偏差≥0.3°。

表2 仿真計算條件Tab.2 Simulation calculation conditions

3.1 不同彈丸形態炮彈引響應特性

按照表2中工況1和工況2對應的仿真計算條件,分別以底凹彈、底排彈不同彈丸形態配用相同引信開展動力學仿真。

9 ms時刻底凹彈發射身管、彈帶響應云圖如圖4所示。

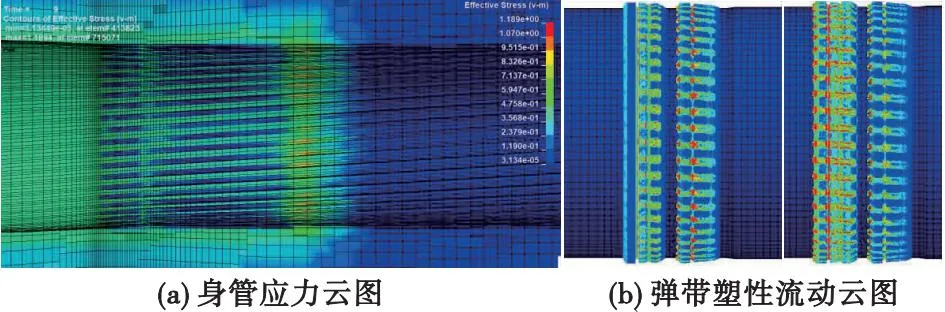
圖4 底凹彈發射后9 ms時刻炮、彈響應云圖Fig.4 Nephogram of gun-howitzer and projectile response at 9 ms after launching

不同彈丸形態彈丸膛內運動過程擠進阻力對比如圖5所示。由圖5可知:0號裝藥相同工況下,底凹彈和底排彈卡膛過程基本一致,約為3.23 ms;彈丸擠進阻力時間歷程基本一致,從3.23 ms時刻開始快速攀升,在7.62 ms時達到峰值,彈帶刻槽過程結束,隨后阻力先快速后緩和下降,在出炮口前擠進阻力消失;底凹彈和底排彈擠進過程峰值分別為685.25和618.86 kN,相差9.69%,差異較小。

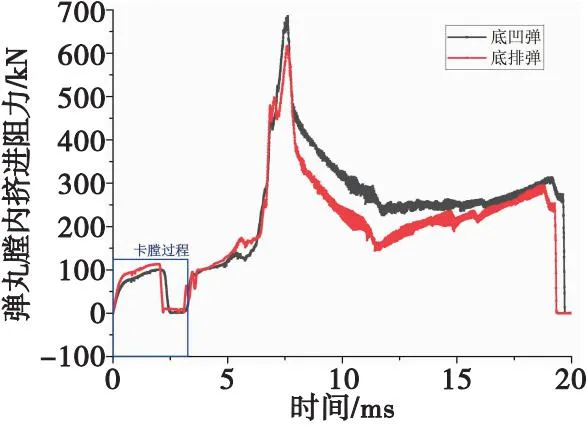
圖5 0號裝藥彈丸擠進阻力對比曲線Fig.5 Charge No.0 projectile extrusion resistance contrast curves

不同彈丸形態彈丸前定心部與身管碰撞力對比如圖6所示。彈丸前定心部與身管撞擊力峰值出現時刻與彈丸擠進阻力時間歷程基本保持一致。其中,底凹彈撞擊力峰值為9.17 kN,底排彈撞擊力峰值為19.6 kN,增大1.14倍。

圖6 0號裝藥彈丸前定心部與身管碰撞力對比曲線Fig.6 Contrast curves of impact force between charge No.0 projectile front centering part and rifled gun barrel

不同彈丸形態彈丸膛內及出炮口階段運動姿態對比曲線如圖7所示。由圖7可知:出炮口瞬間,底凹彈俯仰角約為0.039°、偏航角約為0.009°,底排彈出炮口俯仰角約為0.049°、偏航角約為0.016°。

圖7 彈丸姿態角對比曲線Fig.7 Contrast curves of projectile attitude angle

不同彈丸形態引信安全系統回轉體軸過載響應對比曲線如圖8所示。由圖8可知:當彈帶擠進阻力衰減達到最小時,回轉體軸過載峰值基本達到最大;不同彈丸形態引信回轉體軸承受的過載脈寬基本一致,峰值差異明顯;底凹彈發射回轉體軸軸向過載峰值為15 835.58g、徑向為3 018.51g,底排彈發射軸向過載峰值為17 944.8g、徑向為2 208.15g。

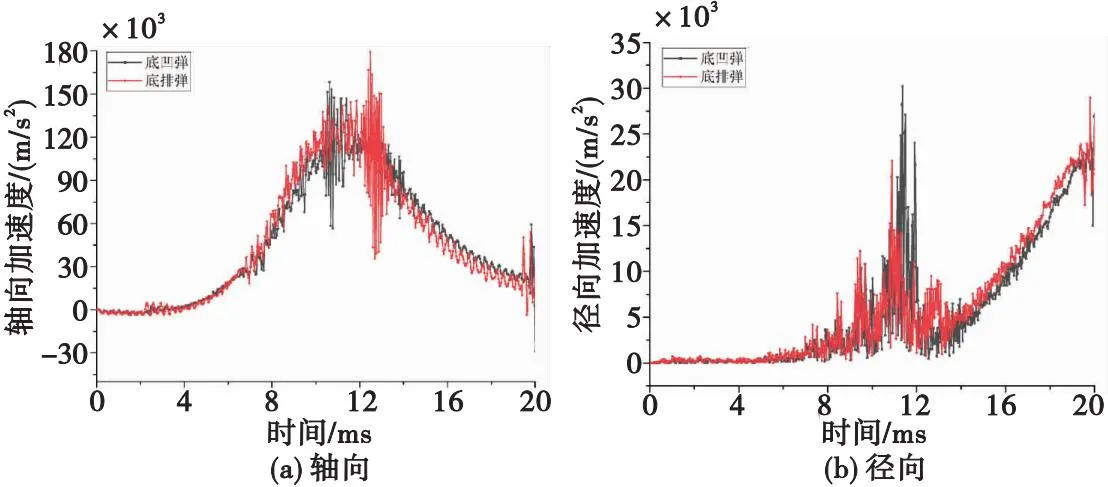
圖8 引信回轉體軸過載響應對比曲線Fig.8 Overload response contrast curves of fuze rotating body

3.2 極限邊界工況炮彈引響應特性

按照表2中工況3對應的仿真計算條件,以身管中后期磨損、底排彈、彈丸最大裝填角、彈丸與引信極限偏差等技術狀態作為炮-彈-引耦合仿真的極限邊界工況,開展動力學仿真。

極限邊界工況彈丸膛內運動過程擠進阻力對比如圖9所示。由圖9可知:極限邊界工況下彈丸卡膛時間約為5.43 ms,比常規工況增加2.2 ms;擠進過程的受力情況和時間歷程曲線與常規工況差異極大,彈帶刻槽過程結束發生在彈丸擠進第一次峰值出現時刻17.53 ms處,對應阻力為493.08 kN;隨后阻力衰減,但衰減程度較常規發射工況小,隨著彈丸膛內姿態的非穩態變化,出現因碰撞產生的振蕩載荷。

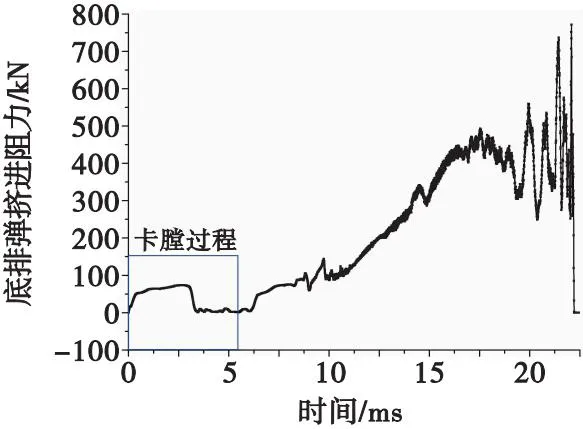
圖9 極限工況彈丸擠進阻力曲線Fig.9 Projectile extrusion resistance contrast curves in limit boundary conditions

極限邊界工況彈丸前定心部與身管碰撞力對比如圖10所示。由圖10可知:彈丸前定心部與身管撞擊力峰值出現時刻與彈丸擠進阻力時間歷程基本保持一致;撞擊力峰值為584.56 kN,是底凹彈撞擊力峰值的63.75倍,是底排彈的29.82倍。

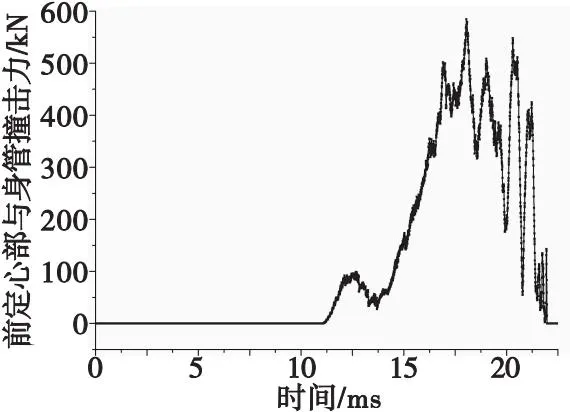
圖10 極限工況彈丸前定心部與身管撞擊力Fig.10 Contrast curves of impact force between projectile front centering part and rifled gun barrel in limit boundary conditions

極限邊界工況彈丸膛內及出炮口階段運動姿態角變化曲線如圖11所示。

圖11 極限邊界工況彈丸姿態角變化曲線Fig.11 Contrast curves of projectile attitude Angle in limit boundary conditions

由圖11可知:隨著彈丸擠進阻力的增大、彈帶刻槽深度的增加,彈丸在膛內大幅擺動,姿態角大幅增大,且跟隨彈丸擠進阻力的變化產生接近周期性的振蕩變化;在出炮口瞬間,其俯仰角為約0.378°、偏航角約為0.044°,相比底凹彈常規工況分別增大8.69倍和3.89倍,相比底排彈常規工況分別增大6.71倍和1.75倍。

極限邊界工況引信安全系統回轉體軸過載響應曲線如圖12所示。

圖12 極限邊界工況引信回轉體軸過載響應曲線Fig.12 Overload response contrast curves of fuze rotating body in limit boundary conditions

由圖12可知:回轉體軸承受軸向過載峰值出現時刻為15.99 ms,處于彈丸擠進阻力達到第一次峰值上升段,峰值大小為18 921.65g,比底凹彈常規工況增大19.49%,比底排彈常規工況增大5.44%;徑向過載膛內出現兩次峰值,第二次持續時間較短,屬于瞬間碰撞帶來的脈沖信號,因此主要分析第一次峰值響應,出現時刻為18.39 ms,處于彈丸擠進阻力達峰后衰減階段,基本與阻力最小值出現時刻相近,峰值大小為5 394.06g,比底凹彈常規工況增大78.7%,比底排彈常規工況增大1.44倍。

4 試驗驗證

分別以底凹彈、底排彈0號裝藥典型工況靶場試驗測試得到引信在膛內承受軸向過載峰值作為特征參量,對炮-彈-引耦合動力學仿真響應模型的預測誤差進行驗證。試驗所用火炮為大口徑加榴炮,彈丸為大口徑底凹榴彈砂彈、底排榴彈砂彈,引信為機械觸發引信加裝加速度測試采集裝置的改裝引信,彈引合裝時通過調整填砂重量和位置實現試驗樣機與實際使用彈丸的彈道參數一致。

測試和仿真結果對比如表3所示。可知,基于底凹彈的炮-彈-引耦合動力學模型仿真預測誤差為10.91%;基于底排彈的仿真預測誤差為10.09%。造成測試和仿真結果誤差的主要原因包括:炮-彈-引耦合動力學模型未考慮彈丸發射藥燃燒過程;靶場試驗測試時火炮身管磨損狀態非典型狀態;傳感器測試本質誤差(約1%)難以消除。

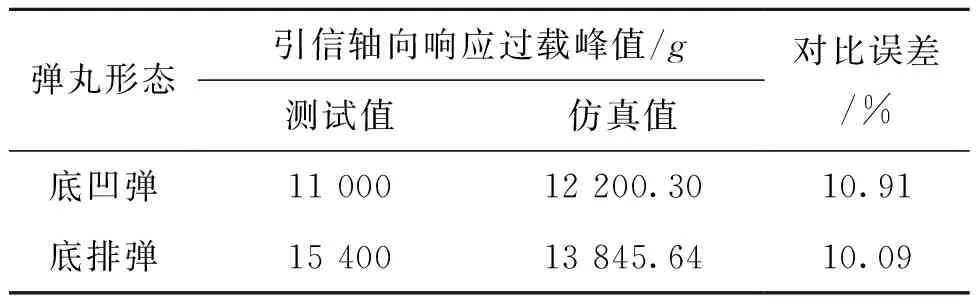
表3 測試和仿真結果對比情況Tab.3 Comparison of test and simulation results

5 結論

本文采用融合SPH和Lagrange的有限元計算方法,對考慮身管中后期磨損、底排彈、彈丸最大裝填角、彈丸與引信極限偏差等極限邊界工況的內彈道環境炮-彈-引耦合響應特性進行了仿真計算和試驗驗證。基于分析結果可得出如下結論:

1) 極限邊界工況對彈丸卡膛時間、彈丸擠進過程承受的阻力以及前定心部與身管撞擊力的時域分布特征影響顯著。相比底凹彈或底排彈常規發射工況,彈丸內彈道運動過程中,彈帶刻槽結束時間延后,彈引遭受的高量值擠進阻力持續時間增大,遭受的彈丸前定心部與身管撞擊產生的橫向碰撞力最多增大了63.75倍,是導致引信徑向過載增大的重要因素。

2) 極限邊界工況對彈丸膛內和出炮口階段運動姿態的影響顯著。相比底凹彈或底排彈常規發射工況,彈丸的姿態角幅值和振蕩程度明顯增大,出炮口瞬間,會以最多增大8.69倍的俯仰角和最多增大3.89倍的偏航角進入外彈道飛行階段,是導致初始章動角增大的重要因素。

3) 極限邊界工況對內彈道階段引信及其典型機構過載響應影響較大。相比底凹彈或底排彈常規發射工況,引信回轉體軸遭受的軸向過載最多增大了19.49%,徑向過載最多增大了1.44倍,是導致其強度失效的重要因素。