基于學情分析的精準教學實踐
——以“百分數的概念建構”的教學為例
江蘇省南京市科睿小學 仇學春
江蘇省南京市瑯琊路小學 張冬梅
“百分數”是小學數學傳統的教學內容,百分數源于分數,源自分數的“率”,表示兩個數或數量的倍數關系。過去的課程標準一般把百分數作為“數與代數”領域的重要內容。《義務教育數學課程標準(2011 年版)》在第二學段“數的認識”部分要求“理解小數和分數的意義,理解百分數的意義”,并在案例部分說明“百分數是同分母(統一標準)的比值,便于比較。希望學生能夠理解它們的含義,在生活中能夠合理使用” 。《義務教育數學課程標準(2022 年版)》則將百分數作為“統計與概率”領域的內容,要求“結合具體情境,探索百分數的意義,能解決與百分數有關的簡單實際問題,感受百分數的統計意義”。具體地說,要引導學生“知道百分數是兩個數量倍數關系的表達,既可以表達確定的數據,如飲料中果汁的含量、稅率、利息和折扣等,也可以表達隨機的數據,如某籃球運動員罰球命中率、某城市霧霾天數所占比例等”。這樣的改變豐富了百分數概念的內涵,將百分數作為一個重要的統計特征量加以認識,突出了其統計意義。
一、學情調查
在教學百分數的意義之前,為了了解學校六年級學生有關百分數意義的“前概念”,精準實施教學,筆者結合學生可能的數學經驗設計了以下三個問題,對學校200 名學生進行了調查。調查采取書面答題的形式,學生在20 分鐘內獨立完成后上交。
1.下面信息中的數叫作百分數。對于這些百分數,你是怎樣理解的?(可以畫圖、舉例說明)
(1)六(2)班男生人數占全班人數的45%。
(2)今年全市空氣質量為優的天數比去年增加了12%。
2.調查發現,五年級有15%的同學近視,六年級有12%的同學近視。小亮認為,五年級近視的同學一定比六年級近視的同學多。對此,你有什么看法?
3.六(2)班的王恒和張兵是足球愛好者,有一天他們練習踢點球,王恒的命中率是80%,張兵是75%。誰點球踢得好?如果再比一次,還一定是王恒踢得好嗎?
第1 題側重了解學生對百分數表示確定數據倍數關系的理解,第2 題側重了解學生對百分數表示的百分率的認識,第3 題側重了解學生對百分數表示隨機數據關系的理解,分析學生的隨機意識。
二、調查結果及分析
為了更深入地了解學生的“前概念”,筆者對調查結果進行了細致的分析,嘗試從學生關于百分數認識的已有基礎、認知水平和發展可能性三個維度進行。“已有基礎”側重了解學生關于百分數的知識經驗和生活經驗,“認知水平”側重了解學生“前概念”的理解層次及表征方式,“發展可能性”側重了解學生百分數概念的素養表現及發展水平,筆者將其形成了“三維度六方面”學情分析框架(如圖1)。

圖1
(一)學生有關百分數概念的已有基礎
學生已經有了分數學習的經驗,對百分數意義的理解有了一定的認知基礎,同時在日常生活中他們或多或少也了解了一些百分率。第1 題的調查結果表明:所有學生都能準確理解并表征“六(2)班男生人數占全班人數的45%”的含義,但是在表征百分數意義的方式上有些區別,67%的學生能用不同的圖形來表示并能準確地加以解釋,25.5%的學生習慣用文字表示,有7.5%的學生則習慣用算式表示。在用圖形表征的學生中,有32.8%的學生選擇用圓形圖表示,24.6%的學生選擇用線段圖表示,42.6%的學生選擇用矩形圖表示。
值得注意的是,只有約66.7%的學生能夠較準確地理解“今年全市空氣質量為優的天數比去年增加了12%”的含義。
百分數的本質是表示一個比率,每個百分數所表示的具體數量既和它本身的大小有關,也和它整體的數量有關。第2 題的調查結果:20.5%的學生認為,15%>12%,所以五年級近視的人數一定比六年級的多;79.5%的學生認為“不一定,因為兩個年級的人數不知道”,其中有學生能夠借助舉例來說明具體的數量多少。
第3 題的調查結果:66.7%的學生認為一定是王恒踢得好,理由是80%>75%;33.3%的學生認為不一定,理由是再踢一次不一定是王恒踢得好。
(二)學生有關百分數概念的表征水平
對于第1 題的第(2)小題用百分數表示一個量和另一個量的倍數關系,學生的認知水平表現出了明顯的區別,于是筆者又進一步分析學生對于這一情境中百分數所表示意義的表征水平層次。具體結果如表1 所示。
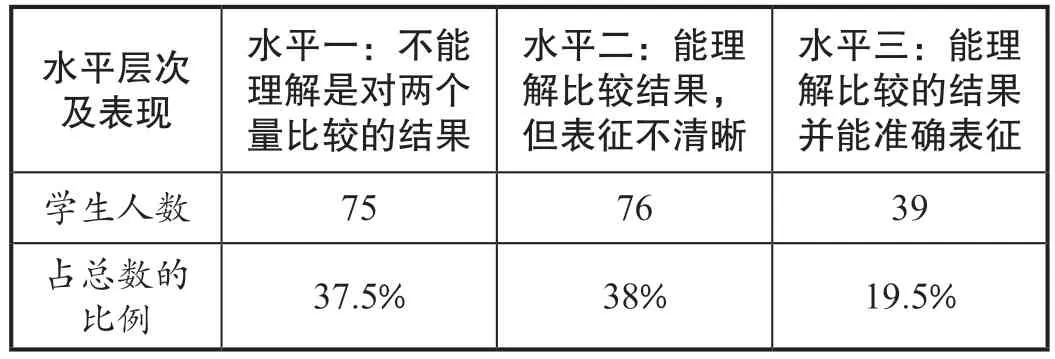
表1 學生對百分數表示一個量和另一個量的倍數關系的表征水平層次結果

表2 六年級男生1 分鐘跳繩情況統計表
水平一:不能理解這里的百分數表示的是對兩個量進行比較的結果。這部分學生只表示出去年的12%,未能清楚地表征“今年比去年增加的部分”與去年比較的關系(如圖2)。

圖2
水平二:僅能理解這里的百分數表示的是對兩個量比較的結果。這部分學生知道12%是今年比去年增加的,但未能表征增加的12%的單位“1”是去年的(如圖3)。
水平三:能理解這里的百分數表示的是對兩個量比較的結果并能準確表征,有的學生對“12%”的單位“1”給出了更加準確的解釋(如圖4)。

圖4
(三)學生的素養發展的現狀與可能分析
百分數不僅可以表示確定數據的倍數關系,還可以表示隨機數據的倍數關系。因此,這一內容對于學生核心素養的發展主要表現在數學意識方面。而對百分數意義的理解也必然會應用圖形表征,因而有利于發展學生的幾何直觀。同時,百分數在實際生活中應用廣泛,因而有利于發展學生的應用意識。從調查結果來看,66.7%的學生的隨機意識的發展還比較薄弱,38%的學生在借助圖形表征一個量是另一個量的百分之幾時仍感到困難,數的意義理解與形的結合能力還有待發展。從調查涉及的實際問題來看,還有33%左右的學生對實際問題中的百分數的應用理解感到困難,應用意識有待增強。
三、精準實施教學
基于上述對學校六年級學生認識百分數的學情分析,教師更清晰地把握了學生認識百分數的“前概念”,這為教師從已有的知識經驗、思維水平和素養發展等方面引導學生整體建構百分數的意義,實施精準教學提供了很多有益的啟示。
(一)會說話的“百分數”
調查結果表明,學生對于理解部分量占總量的百分數意義比較簡單,但是對于理解兩個相關量的百分比還有一定的難度。因此,教師在教學時要關注百分數意義的抽象概括過程,引導學生真正理解百分數的意義,同時要關注用百分數表示一個數比另一個數多(或少)百分之幾的意義的理解,體會“百分數”會說話。
(1)談話:百分數在生活中有著廣泛的應用,教師也帶來了幾個百分數(如圖5),你知道這些百分數表示的意思嗎?請同學們按照任務單上的內容獨立思考探究,完成后小組內合作交流。

圖5
(2)組織學生匯報交流。
生1:男生人數和全班人數比較,把全班人數看作單位“1”,平均分成100 份,男生人數有這樣的40 份。
生2:九月份用水量和八月份用水量比較,把八月份用水量看作單位“1”,平均分成100 份,九月份用水量有這樣的95.5 份。
生3:今年比去年增加空氣質量為優的天數與去年的比較,把去年空氣質量為優的天數看作單位“1”,平均分成100 份,增加的空氣質量為優的天數有這樣的12 份。
師:這里哪個百分數比較特殊?
生:95.5%比較特殊,它的分子是一個小數。
(3)抽象概括百分數的意義。
師:什么是百分數?你們能用自己的方式表示百分數和分數之間的聯系嗎?
生1:百分數表示一個數是另一個數的百分之幾。
生2:百分數的分母是100,分母是100 的分數不一定是百分數。
(4)理解百分比。
師:根據六(2)班男生人數占全班人數的40%,你能聯想到什么知識?
生1:老師,我想到了女生人數占全班人數的60%。
生2:我發現了女生人數與男生人數的比是3∶2。
生4:還可以這樣說,男生人數是女生人數的
師:百分數和分數、比、除法這些學過的知識是相互聯系的(如圖6),都可以表示兩個量之間的倍數關系。所以百分數又叫百分比。
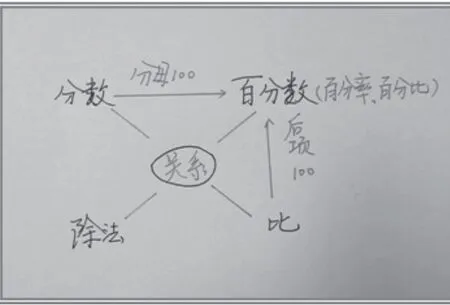
圖6
(5)體會百分數表示的具體數量與單位“1”有關。
師:學校繪畫組男生占總數的10%,學校書法組男生占總數的12%,哪個組的男生多?
生1:因為12%大于10%,所以書法組的男生多。
生2:無法確定,因為不知道兩個組的人數。
師:這里的百分數表示的大小與什么有關?
生:既與單位“1”有關,還與本身的大小有關。
(二)調皮的“命中率”
調查結果表明,66.7%的學生的隨機意識的發展還比較薄弱,他們對于百分數可以表示隨機數據的倍數關系的認識還比較模糊。因此在教學時,教師應幫助學生強化對“命中率”意義的理解,引導學生體會“命中率”是通過抽樣或調查得到的,如果用一次抽樣或調查的結果來分析、判斷,所得到的結論不能“百分之百”地成立,要考慮數據本身的“隨機性”。當然,還可以讓學生在具體情境中自己確定標準,體會百分數的統計意義,增強數據的隨機意識。
(1)出示任務:(如圖7)

圖7
師:誰的點球踢得好?
生1:我認為王恒踢得好,因為80%大于75%。
生2:我認為不能確定誰踢得好,因為不知道踢的總次數。
生3:如果總次數一定,我認為是王恒踢得好,因為王恒踢進的個數多。
師:如果再比一次,你覺得誰會贏?
生1:我認為王恒不一定贏,因為王恒每一場點球的命中率可能不一樣,第一場的命中率是80%,第二場的命中率可能高于80%。也可能低于80%。
生2:兩個人都有可能贏,就要看誰臨場發揮得好。
生3:我覺得王恒贏的可能性大一些,畢竟他的命中率更高。
師:王恒踢點球1 次,踢中1 次,命中率100%;另一次比賽,他踢點球10 次,踢中8 次,命中率80%。哪個“命中率”能代表他的水平呢?
生1:肯定是80%,因為踢的次數少沒有代表性。
生2:踢的次數多一點,統計命中率就會準一些。
師:是的,如果讓王恒踢點球50 次,踢中40 次;踢點球500 次,踢中401 次……直至踢更多的次數,這時他的點球命中率大約是80%。只有擁有足夠多的數據時,命中率才是可靠的。
師:通過對點球命中率的研究,你還能想到哪些百分率?
生1:出勤率,如六(1)班有50 人,實際到校48 人,出勤率為96%。
生2:我還想到優秀率、及格率……
師:通過對命中率、出勤率的研究,你們對百分數又有什么新的認識?
生1:百分數可以表示兩個隨機數據之間的關系。
生2:命中率要統計更多的數據才是準確的。
師(小結):百分數既可以表示確定的數據,也可以表示隨機的數據。
(2)小組合作制定六年級男生1 分鐘跳繩的標準。
師:小組商量怎樣制定六年級男生1 分鐘跳繩標準。
生1:我們先要收集六年級所有男生1 分鐘跳繩的數據,然后整理數據。
生2:我們可以統計六年級男生跳繩個數的平均數,再制定標準。
生3:也可以根據他們跳繩的情況,借助百分數定標準。
師:要收集數據、整理數據、分析數據,最后才能制定標準。根據表1 中的數據,你們能制定六年級男生1分鐘跳繩的標準嗎?并說一說這樣制定的理由。
生1:我們小組劃分了優秀、良好、合格和不合格四個等級比例各占25%,比例均等。
生2:99 個及以下定為不合格,占17%; 100~119個定為合格,占22%;120~159 個定為良好,約占55%;160 個及以上為優秀,占6%。大多數人能得良好。
生3:我們小組將160 個及以上定為優秀,占14%,120~159 個定為良好,占47%;80~119 個定為合格,占32%;80 個以下定為不合格,占7%。
師(評價):第一種各占25%,不合格和優秀的人數都偏多;第2 種優的人數比例偏少,不合格和良好的人數偏多;第3 種更多的人達標,容易調動同學們跳繩的積極性。
(2)表3 是《國家學生體質健康標準》中六年級男生1 分鐘跳繩標準:
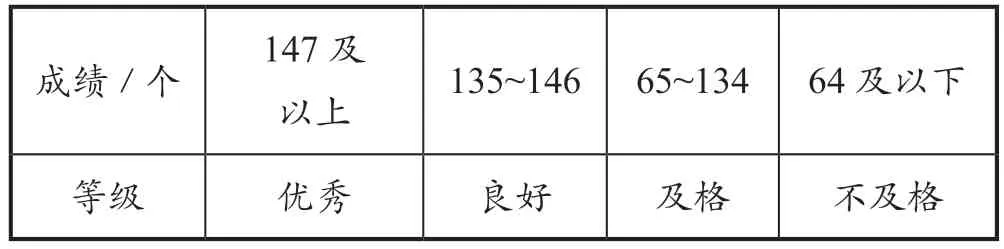
表3 六年級男生1 分鐘跳繩標準
師:對比國家1 分鐘男生跳繩標準,你們有什么想說的?
生1:我們制定的標準比國家的標準要高不少。
生2:對比國家標準,說明我們學校六年級男生的跳繩成績明顯高于全國的水平。
生3:國家標準可以適當調整,及格所占比例太大,優秀的標準有點低,不利于調動學生的積極性。
……

