無量綱化方法選擇及最優無量綱化方法構建
高曉紅,李興奇
(楚雄師范學院a.數學與計算機科學學院;b.管理與經濟學院,云南 楚雄 675000)
0 引言
無量綱化是指通過某種函數關系將不同指標映射到同一數量級內,以便進行不同指標間重要程度的比較。無量綱化的好處是可以消除指標間的量綱差異,弊端是會改變指標的原貌特征,造成有用信息的損失。現有無量綱化方法眾多,經不同無量綱化方法處理后所得的綜合評價結果不同,導致綜合評價結論難以令人信服。如何科學評價無量綱化方法的利弊,進而選擇恰當的方法對指標進行無量綱化處理成為很多學者研究的重點問題。郭亞軍和易平濤(2008)[1]對常用的線性無量綱化方法進行了分析,分別以單調性、差異比不變性、平移無關性、縮放無關性、區間穩定性、總量恒定性為標準來選擇無量綱化方法,最后證明了不存在同時滿足六條性質的理想無量綱化方法;部分研究通過多種無量綱化方法評價結果的Spearman相關系數來構建無量綱化方法的相對有效性指標,并基于此來選擇無量綱化方法;易平濤等(2014)[2]通過無量綱化方法的穩定性來評價無量綱化方法的優劣,并進行無量綱化方法選擇;李玲玉等(2016)[3]根據變異性原則、差異性原則和穩定性原則來選擇無量綱化方法,并得出線性比例法是適合于拉開檔次法的最佳無量綱化方法的結論;李興奇和高曉紅(2021)[4]通過評價無量綱化方法的有效性來進行方法選擇;謝忠秋(2020)[5]用各指標的方差大小來度量信息總量,并通過比較無量綱化方法前后信息總量改變情況來構建檢驗統計量,提出了一種檢驗無量綱化方法有效性的t檢驗方法,使得無量綱化方法選擇更加客觀,但其只考慮了無量綱化方法的效果,未顧及無量綱化可能造成的信息損失。此外,還有很多學者通過研究無量綱化方法對綜合評價結果的影響來進行無量綱化方法選擇[6—9]。
現有研究對綜合評價模型中無量綱化方法的選擇沒有統一的標準,且不具備可操作性,很多無量綱化方法選擇只停留在思想層面,在實際操作過程中難以明確具體應該選擇哪一種方法對特定的數據進行無量綱化處理,很多環節帶有一定的主觀性,需要憑借研究者的經驗或偏好才能確定最終的無量綱化方法。基于此,本文通過權衡無量綱化方法的利弊,構建一種檢驗無量綱化有效性的F 檢驗方法,并基于原貌特征不變性、方法有效性等原則來進行無量綱化方法選擇,最終以無量綱化應在有效消除指標間量綱差異的情況下盡可能地減小有用信息的損失為原則構建最優無量綱化方法,在保證無量綱化方法有效的條件下避免對數據的過度處理,造成過多的信息損失。
1 無量綱化方法的分類及性質
無量綱化是指通過某種函數關系將不同指標的數值映射到同一量綱級內,便于不同指標間的比較。根據函數關系可將其分為非線性無量綱化和線性無量綱化。非線性無量綱化是通過非線性函數建立原始數據xij與可比數據yij之間的關系,線性無量綱化則是通過線性函數建立兩者之間的映射關系。通用公式為yij=kj()xij-aj,其中,xij為第j項指標的第i個觀測值,aj和kj分別表示第j項指標的平移尺度和伸縮尺度。根據aj和kj取值的不同又可將線性無量綱化方法分為平移法、伸縮法和平移伸縮法,當aj=0 且kj≠0 時為伸縮法,函數關系為yij=kjxij;當aj≠0且kj=1時為平移法,函數關系為yij=xij-aj;其余情況均屬平移伸縮法,其中,i=1,2,…,m,j=1,2,…,n。常用的無量綱化方法如表1所示。
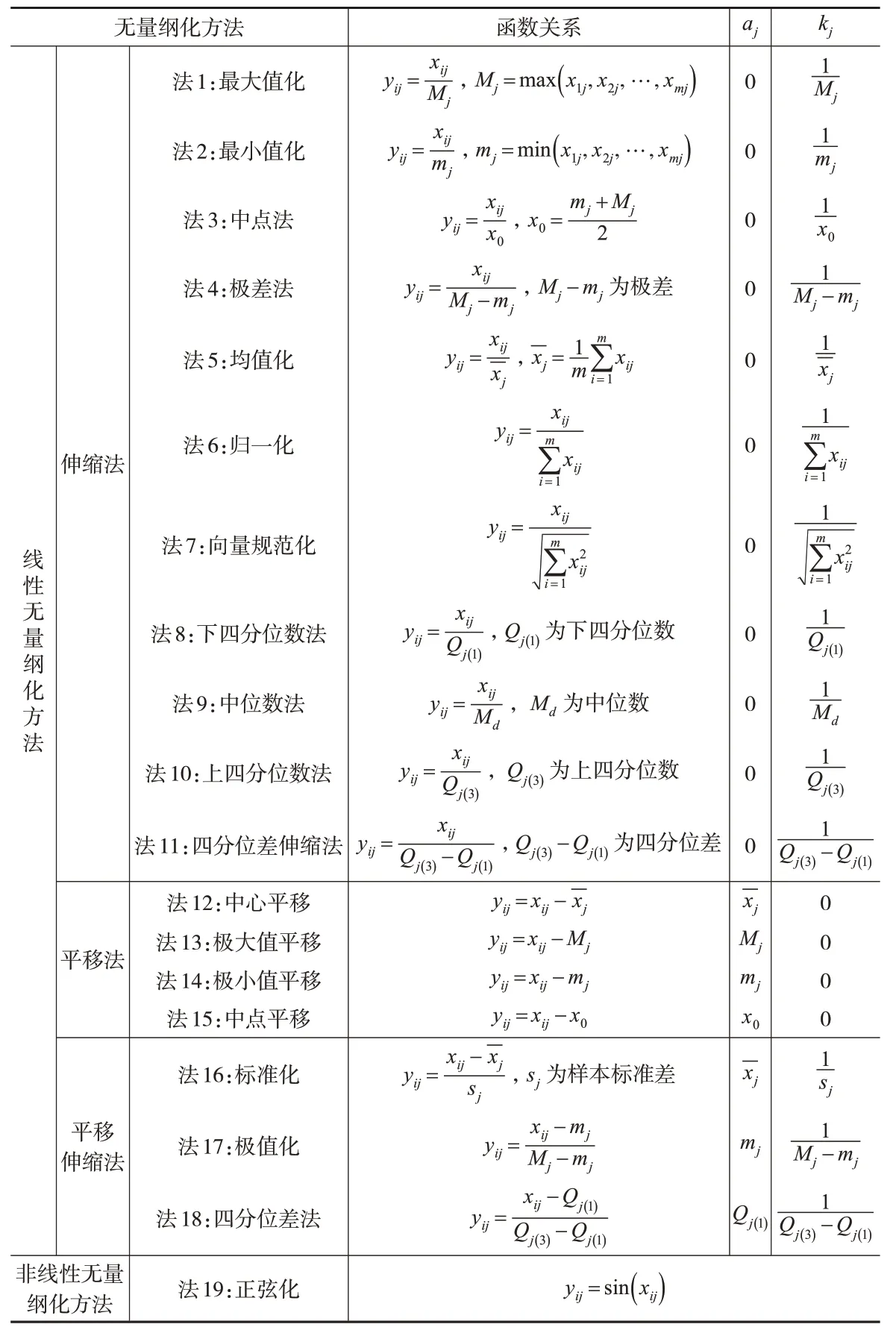
表1 無量綱化方法的分類、函數關系及平移、伸縮尺度
無量綱化的優點是消除指標間的量綱差異,缺點是容易改變指標的原貌,而綜合評價結果往往依賴于指標的分布特征和變異特征,所以好的無量綱化方法應該保持指標的分布特征和變異特征不變。李興奇和高曉紅(2021)[4]分別用偏度系數和峰度系數來度量指標的分布特征,用變異系數和相對極差來度量指標的變異特征,并通過比較無量綱化前后指標分布特征和變異特征的變化情況來研究無量綱化方法的性質,結果發現,只有伸縮法能同時保持指標的分布特征和變異特征不變,非線性無量綱化會同時改變指標的分布特征和變異特征,平移法及平移伸縮法不改變指標的分布特征但會改變其變異特征。
2 無量綱化方法的有效性檢驗
基于分布不變性和變異特征不變性發現,伸縮法是眾多無量綱化方法中最能夠保持指標原貌的方法,但其有效性沒有得到進一步的檢驗,所以有必要構建一種可以檢驗其有效性的統計方法。無量綱化方法的有效性是指將綜合評價指標體系經過某種無量綱化處理后指標間的量綱差異消除的效果。能成功消除指標間量綱差異的方法即有效方法,所以度量指標間量綱差異的大小是檢驗無量綱化方法有效性的首要工作。因指標間的量綱差異主要來源于單位和數量級差異,而指標間是否存在單位差異可以通過指標的內涵來判斷,所以度量指標間量綱差異大小的關鍵是度量指標間的數量級差異。當兩項指標維數較高且取值不同時,無法通過逐一比較的方式來判斷指標間是否存在量綱差異,必須對指標信息加以綜合來比較,均值作為數據平均取值情況的綜合性指標,通過各指標均值間的相互比較可判斷不同指標是否存在數量級差異,所以檢驗各指標間是否存在數量級差異的關鍵就是檢驗各指標的均值是否存在明顯的差異。綜上所述,通過檢驗各指標的均值是否存在顯著的差異來判斷指標間是否存在量綱差異。
假設現有一個由n項指標構成的綜合評價指標體系,每項指標擁有m個樣本觀測值,即,其均值為。相當于利用n項指標對m個對象進行綜合評價。指標體系X經過無量綱化處理后的結果記為Y,且Y=[Y1Y2…Yj…Yn] ,Yj表示Xj經無量綱化后的結果,,其均值為。為提高統計檢驗的科學性,假設每項指標均來自方差相同、均值各異且觀測值相互獨立的正態分布總體,即Yj~N(μj,σ)。
2.1 原假設和備擇假設
均值作為指標間數量級大小的主要度量指標,檢驗指標間是否存在量綱差異的關鍵是通過樣本觀測值來判斷總體均值是否存在顯著差異,若總體中各指標的均值相等,則認為各指標間不存在明顯的量綱差異;若總體中各指標的均值互不相等,則認為各指標間存在明顯的量綱差異。所以可通過檢驗無量綱化后各指標所屬總體的均值是否相等來判斷無量綱化方法是否有效,若經無量綱化后各指標均值已無顯著差異,則認為該無量綱化方法能有效消除指標間的量綱差異,即方法有效;反之則不能認為該無量綱化方法有效。基于此構建無量綱化方法有效性檢驗的原假設H0和備擇假設H1。
H0:μ1=μ2=…=μn,各指標間不存在量綱差異,無量綱化方法有效。
H1:μ1,μ2,…,μn不全相等,各指標間存在量綱差異,無量綱化方法無效。
2.2 檢驗統計量
指標體系X經過無量綱化的結果Y中必然存在數據間的差異,總體差異大小可用各觀測樣本與整體平均水平間的偏差平方和來刻畫,記作表示整個評價指標體系的總平方和,其中;指標間的差異大小可用各指標的平均水平與整體平均水平的偏差平方和來刻畫,記作,表示組間平方和;指標內的差異大小可用各指標取值yij與指標平均水平的偏差平方和來刻畫,記作,表示組內平方和。三種平方和間滿足SST1=SSA1+SSE1。當總體平方和SST1一定時,指標間平方和與指標內平方和滿足此消彼長的關系,為盡可能支持原假設H0,希望指標間平方和盡可能小,而指標內平方和盡可能大。所以可用指標間平方和與指標內平方和的比值來構建檢驗統計量,但容易發現,三種平方和容易受指標選取數量和樣本觀測個數的影響,所以分別除以各自的自由度得到指標間均方和以及指標內均方和,將兩個指標進行相互比較得到檢驗統計量為:
指標間均方和越大,指標內均方和越小,統計量F的取值越大;反之,指標間均方和越小,指標內均方和越大,統計量F的取值越小,并且F分別服從自由度為(n-1)和(mn-n)的F分布,簡記為F~F(n-1,mn-n)。給定顯著性水平α時,可計算其分位數Fα(n-1,mn-n)。當F>Fα(n-1,mn-n)時,檢驗統計量落在拒絕域內,應該拒絕原假設,即經無量綱化后各指標間依然存在顯著的量綱差異,表明該無量綱化方法無效;否則認為經無量綱化后各指標間不存在明顯的量綱差異,該無量綱化方法有效。
3 無量綱化方法的信息損失速率
通過無量綱化的有效性檢驗能科學準確地判斷某種無量綱化方法是否能成功消除指標間的量綱差異,避免方法選擇的盲目性,但在有效性檢驗過程中沒有考慮到無量綱化可能帶來的有用信息損失,這可能會造成數據的過度處理。一種好的無量綱化方法應該能有效消除指標間量綱差異,同時盡可能使有用信息的損失速率最小。無量綱化方法的信息損失速率是指每消除一個單位的量綱差異所造成的內部差異信息損失大小,其中,可用無量綱化前后的指標內均方和之差(MSE0-MSE1) 來表示指標內的差異信息損失大小,用無量綱化前后指標間均方和之差(MSA0-MSA1) 來表示指標間的差異信息損失大小,用兩者的比值表示每消除一個單位的量綱差異所造成的信息損失,即無量綱化方法的信息損失速率:
其中,MSE0和MSA0分別表示無量綱化前原始數據的指標內均方和與指標間均方和,MSE1和MSA1分別表示經無量綱化后數據的指標內均方和與指標間均方和。理想的無量綱化方法應該在有效消除指標間量綱差異的同時完全保留指標內的有用信息,但這種理想狀態一般無法達到,因為在縮小指標間量綱差異的同時往往會造成指標內差異信息的損失。無量綱化方法的信息損失速率能準確度量在縮小指標間量綱差異的過程中所造成有用信息的損失大小。
4 無量綱化方法的選擇步驟
根據分布不變性和變異特征不變性可證明伸縮法是眾多無量綱化方法中最能保持指標原貌的方法,通過無量綱化的有效性檢驗能判斷所選無量綱化方法是否能成功消除指標間的量綱差異,通過信息損失速率能準確度量無量綱化過程中所造成的信息損失情況。一般情況下,在選擇無量綱化方法時應該選擇不會改變指標分布特征和變異特征,同時能有效消除指標間量綱差異,并且信息損失速率最小的方法。基于此,提出無量綱化方法選擇的三個步驟:
步驟1:從眾多無量綱化方法中選擇不改變指標分布特征和變異特征的無量綱化方法。經證明,伸縮法是一種既不改變指標分布特征又不改變其變異特征的無量綱化方法,但現有的伸縮法眾多且未必都有效,所以需進行第二步篩選。
步驟2:從伸縮法中選出有效的無量綱化方法。在給定的顯著性水平下,分別計算出檢驗統計量F和α分位數Fα,通過比較兩者間的大小來判斷無量綱化方法是否有效,當F 步驟3:從有效的伸縮法中選出信息損失速率最小的無量綱化方法。當有多種伸縮法均有效時,需進一步進行方法選擇,可分別計算各種有效無量綱化方法的信息損失速率,從中選擇信息損失速率最小的無量綱化方法。基于此,可從眾多無量綱化方法中選出合適的方法對指標數據進行無量綱化處理,避免了傳統方法選擇時的盲目性和主觀性。 現有方法大多基于常用的數字特征來計算伸縮法的比例系數,如最大值、最小值、均值、分位數等,而比例系數的取值范圍不僅僅局限于此,所以本文構建一種求解最佳比例系數的無量綱化方法。當利用伸縮法對指標進行無量綱化處理時,原始數據與無量綱化后數據間存在函數關系Yj=kj Xj,其中,kj為第j項指標的比例系數,由所有指標的比例系數構成向量k,k=()k1,k2,…,kj,…,kn,當k取何值時,能在保證無量綱化方法有效的前提下盡可能地減少有用信息的損失,同時實現指標間量綱差異消除與防止數據過度處理?基于此,構建如下求解最佳比例系數的非線性規劃模型: 通過MATLAB 軟件產生方差均為100、均值在10 到10000間的10組正態分布隨機數,每組隨機數中產生5000個樣本觀測值,分別為:X1~N(10,102),X2~N(50,102),X3~N(100,102),X4~N(200,102),X5~N(500,102),X6~N(1000,102),X7~N(2000,1 02),X8~N(5000,102),X9~N(8000,102),X10~N(10000,102)。相當于利用10個指標對5000個對象進行綜合評價,所有指標構成的綜合評價指標體系為X=(X1,X2,…,X10)。容易發現10項指標間存在明顯的量綱差異。 通過MATLAB 軟件計算10 項原始指標的峰度系數、偏度系數和變異系數,并分別利用表1中的19種無量綱化方法對10 項指標進行無量綱化處理,輸出無量綱化后各指標的峰度系數、偏度系數和變異系數,進行無量綱化前后指標分布特征的比較,結果如下頁表2所示。 表2 各指標無量綱化前后的峰度系數、偏度系數和變異系數 從表2可以看出,經線性無量綱化(法1至法18)處理后10 項指標的峰度系數和偏度系數均未改變,而經非線性無量綱化(法19)處理后各指標的峰度系數和偏度系數均發生了改變,說明線性無量綱化不會改變指標的分布特征,而非線性無量綱化通常會改變指標的分布特征。從變異系數來看,經伸縮法(法1至法11)處理后指標的變異性不變,經其他方法處理后的變異系數均發生了改變,說明伸縮法不會改變指標的變異特征,其中,因第一項指標的最小值為負數,所以經最小值化(法2)處理后其變異系數為負,但其大小不變,故認為其變異特征沒有發生改變。綜上所述,伸縮法既不會改變指標的分布特征,也不會改變指標的變異特征,是一類最能保持指標原貌的無量綱化方法,但伸縮法中包含的具體方法依然較多,需進一步進行方法選擇。 當給定顯著性水平α=0.05 時,可通過軟件計算得到自由度為9和49990的0.05分位數為Fα(9,49990)=1.88007。分別計算各伸縮法的檢驗統計量,并對方法的有效性進行檢驗,結果如表3所示。 表3 伸縮法的有效性檢驗統計量 從表3 可以看出,各伸縮法的檢驗統計量大小不一,只有法5(均值化)、法6(歸一化)和法9(中位數法)的檢驗統計量小于0.05分位數,其余方法的檢驗統計量均大于或遠大于0.05 分位數。這表明,在0.05 的顯著性水平下,只有均值化、歸一化和中位數法能有效消除指標間的量綱差異,其余方法未能有效消除指標間的量綱差異。所以在選擇無量綱化方法時一定要注重其效果的檢驗,若方法選擇不當,則指標間的量綱差異不能被有效消除。針對特定的綜合評價指標體系X,有三種方法能夠成功消除指標的量綱差異,但最終應選擇哪種方法對其進行無量綱化處理還存在一定的疑問,所以需要對三種有效方法再次進行篩選,得到唯一確定的無量綱化方法。 無量綱化的目的是消除指標間量綱差異的同時盡可能減小指標內的信息損失,通過計算有效無量綱化方法的信息損失速率,可從現有的無量綱化方法中選出最適合的方法對指標進行無量綱化處理。 從表4 可以看出,三種有效無量綱化方法的信息損失速率均較小且互不相同,其中法9 的信息損失速率最小,法5 的信息損失速率居中,法6 的信息損失速率最大。表明針對特定的綜合評價指標體系X,中位數法是19 種無量綱化方法中能在有效消除指標間量綱差異的同時使信息損失速率最小的方法。通過以上操作發現,根據無量綱化方法選擇的三個步驟可從現有方法中選出最適合的無量綱化方法,當綜合評價指標體系發生變動時,最適合的無量綱化方法可能隨之變更,避免了一勞永逸的缺陷。 表4 有效無量綱化方法的信息損失速率 從現有方法中選出的最適合的無量綱化方法未必是最優的,所以針對特定的綜合評價指標體系X,通過求解非線性規劃模型(3)得到最優無量綱化方法中各指標的伸縮比例系數和有效性檢驗統計量。 從下頁表5 可以看出,最優無量綱化模型中的比例系數不同于三種有效無量綱化方法中的任何一種,但與中位數法和均值化的比例系數較為接近,與歸一化的比例系數相差較遠,這也是中位數法和均值化總體上優于歸一化的主要原因。另外,最優無量綱化模型的有效性檢驗統計量略小于0.05 分位數,表明最優無量綱化方法是有效的。所以最優無量綱化模型能實現在有效消除指標間量綱差異的情況下使信息損失最小,避免對數據的過度處理,并且最優比例系數會隨著綜合評價指標的變化而變化,使用較為靈活。 表5 最優伸縮比例系數 本文針對無量綱化方法選擇困難的問題,依據無量綱化分布不變性、變異不變性、有效性和信息損失快慢的度量指標,提出了無量綱化方法的選擇步驟,并通過大量的數值模擬分析進行19種無量綱化方法的選擇和最優無量綱化模型的求解,結果發現: (1)非線性無量綱化方法會改變指標的分布特征和變異特征,平移法和平移伸縮法能保留指標的分布特征但會改變其變異特征,伸縮法是一種既不改變指標分布特征也不改變指標變異特征的方法。 (2)在選擇無量綱化方法時,需綜合考慮其分布不變性、變異不變性、有效性和信息損失大小,通過無量綱化方法選擇的三個步驟,可從現有方法中選出最適用的無量綱化方法,避免了方法選擇的盲目性。 (3)最優無量綱化模型實現了在有效消除指標間量綱差異的情況下使信息損失最小,可以防止對數據的過度處理,造成不必要的信息損失。5 最優無量綱化方法構建
6 仿真模擬實驗
6.1 無量綱化方法的分布不變性和變異不變性論證
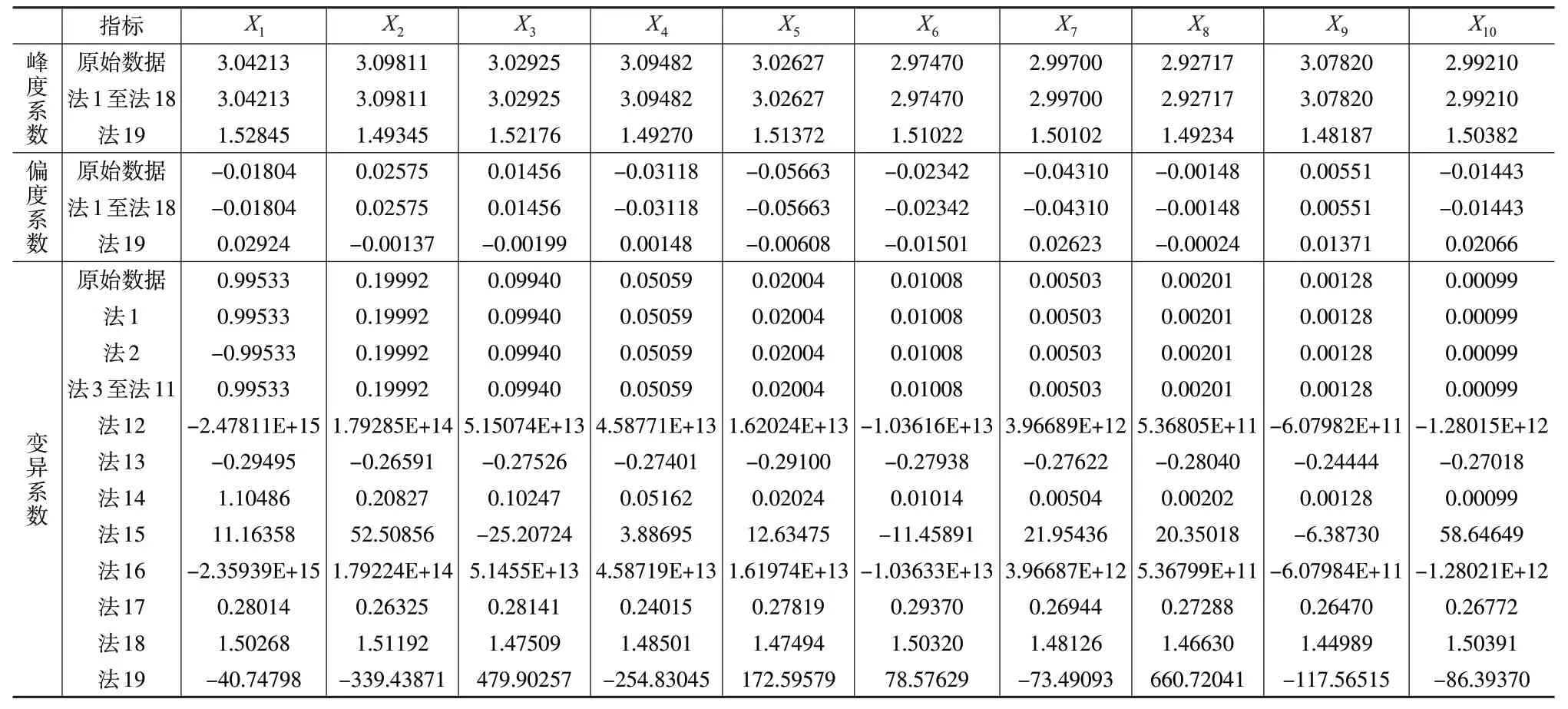
6.2 伸縮法的有效性檢驗結果
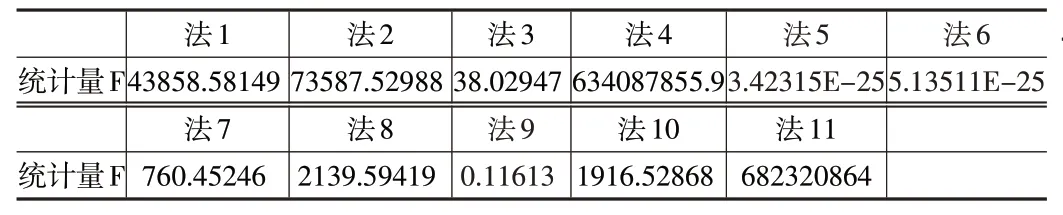
6.3 有效無量綱化方法的信息損失速率

6.4 最優無量綱化模型的求解
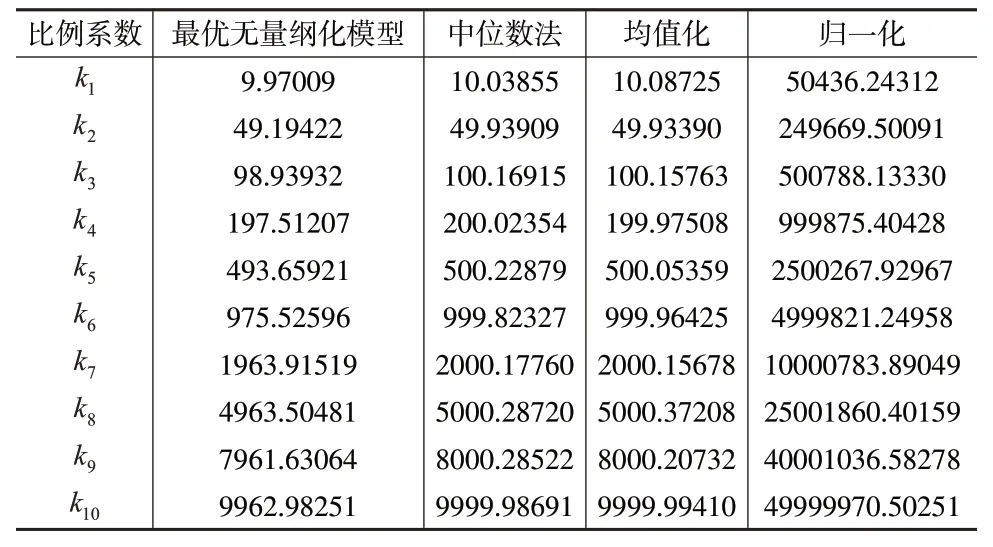
7 結論

