基于光滑粒子流體動力學的波浪中航行體入水數值模擬

管祥善，孫鵬楠，2，*，李江昊，孫龍泉

(1. 中山大學 海洋工程與技術學院，珠海 519000；2. 中國空氣動力研究與發展中心 結冰與防除冰重點實驗室，綿陽 621000；3. 哈爾濱工程大學 船舶工程學院，哈爾濱 150001)

0 引言

航行體在波浪中的入水問題一直是海洋工程中研究的熱點和難點，航行體在波浪條件等復雜環境下入水的彈道穩定性，也一直是國防領域中十分關注的問題。航行體在波浪中的入水過程是一種非常復雜的流體力學現象，涉及到水動力學、空氣動力學、剛體動力學等多個學科領域[1]。在高速航行體入水過程中，入水沖擊載荷和運動響應會影響航行體的運動軌跡[2-3]，而波浪在自然界廣泛存在且很難避免，波浪的相位、浪高、頻率等物理參數呈現強隨機性，也會對航行體的入水狀態和運動軌跡產生明顯的影響[4]，進而決定發射任務的成敗[5]。研究真實波浪條件下航行體的入水過程可以更好地了解航行體在波浪中的運動規律以及波浪對于航行體運行軌跡的影響，可為海洋工程和國防領域航行體的設計和優化提供技術支撐，滿足國家重大戰略需求。

針對航行體的入水問題，主要采用理論研究[6-7]、試驗研究[8-11]和數值模擬[12]。 隨著計算機技術的高速發展，數值模擬逐漸成為解決工程問題的主要方法，計算流體動力學 （Computational Fluid Dynamics,CFD）逐漸成為水動力學研究的一種主要手段[13-15]。但是，由于航行體波浪入水問題中包含的復雜物理現象，對其進行準確數值仿真始終是CFD領域最具挑戰性的課題之一。目前，大多數的CFD數值模擬方法是基于網格類方法[16-18]。楊曉光等[19]采用流體體積多相流模型和動網格技術建立高速入水數值模擬方法，并開展靜水工況下航行體入水試驗，驗證了其數值方法的精度，并基于此數值方法對航行體在波浪條件下的高速斜入水過程進行模擬，得到了航行體在不同相位角下的入水軌跡和運動響應結果。盡管網格法可以精確計算航行體入水過程中的水動力載荷，但需要提前對飛濺區域進行網格加密處理才能精確地捕捉大變形液面和飛濺液滴。在模擬自由液面大變形運動時，拉格朗日粒子算法更具優勢[20-22]，該算法易于處理大變形和快速移動的自由表面，以及飛濺的離散液滴，并能捕捉和生成多相流界面，無需額外的界面處理，有利于處理多介質多物理場的耦合[23-26]。光滑粒子流體動力學（smoothed particle hydrodynamics, SPH）方法作為應用最廣泛的粒子類方法，被很多研究者用于模擬航行體的入水問題[27-29]。Zhao等[30]采用SPH方法，對波浪條件下的結構物入水問題和流場細節進行了模擬分析。Yan等[31]采用更新拉格朗日粒子流體動力學方法對復雜結構物的入水問題進行了模擬，并很好地捕捉了剛體入水過程中周圍形成的水冠、空腔形狀和流場細節。航行體在波浪中高速入水的數值模擬，相對于靜水工況，存在著波浪建模、液面劇烈變形及液滴飛濺、剛體六自由度運動響應計算等難點，而針對波浪的SPH方法建模，也往往采用推板造波的方式，并設置消波區來消除波浪反射，這增加了計算規模和復雜度，并且推板造波需要一定的時間形成穩定的波浪，不適合航行體高速瞬時入水的模擬。

因此，本文采用SPH方法，提出一種新型的周期性波浪邊界技術，建立波浪條件下的數值水池，之后采用四元數法計算航行體的六自由度運動，通過SPH方法與四元數法結合，對高速航行體在不同波浪相位角下的入水過程展開數值模擬，得到不同波浪相位角下航行體入水的六自由度運動軌跡，以期為高速入水航行器的工程設計提供計算工具和理論依據。

1 數值計算方法

1.1 SPH方法基本理論

本文采用Antuono等提出的δ-SPH方法[32]，該方法易于實現，與標準弱可壓光滑粒子流體動力學（weakly compressible smoothed particle hydrodynamics,WCSPH）相比，其主要優點是更具穩定性，可避免高頻振蕩下出現非物理能量。

δ-SPH方法的主要控制方程如下：

其中：連續性方程和動量方程右側最后一項分別為密度耗散項和人工黏性項；D/Dt表示跟隨流體微團運動的導數，稱之為對時間t的物質導數或拉格朗日導數；ρ、u和r分別表示流體微團的密度、速度矢量和位置矢量；g為體積力產生的加速度(本文中指重力加速度)；p、V分別代表壓力和體積；α和δ分別為密度耗散項系數和人工黏性系數，本文中皆取0.1；下標i、j表示粒子編號；W為核函數；h為光滑長度；c0、ρ0分別為流體聲速和流體參考密度。

1.2 波浪數值模型

為研究波浪環境下高速航行體入水的沖擊載荷和運動軌跡，本研究基于有限水深波浪理論建立波浪數值模型[33]。波面方程為：

其中：η為波浪在t時刻x位置的高度；初始化時刻t為0；H為波高；ω=2π/T為頻率，T為波浪周期；k=2π/L為波數，L為波長。L可以根據色散方程得到[33]：

其中d為靜水深度。速度勢函數[19]的表達式如下：

其中x和y是橫坐標和縱坐標。根據速度勢函數和水深可以得到波浪某一位置的速度和壓力[33]：

其中u和v分別是x方向和y方向的速度。根據式（5）計算的速度和壓力賦予波浪粒子初始速度和壓力值。

1.3 周期性波浪邊界技術

造波一直是建立波浪數值水池的關鍵問題，如果采用傳統的推板造波方法，需要在波浪演化尾部加入海綿層消波區域來降低波浪的反射，處理相對復雜，計算域也相對較大，且波浪的穩定也需要一定的時間，因此并不適合用于航行體高速入水工況的計算。本文提出一種新型周期性波浪邊界技術，在處理造波問題上具有很大的優勢：只需將波浪數值水池中的SPH粒子按照波浪數值模型賦予初始速度和壓力，流體域長度滿足波長的整數倍，采用周期性邊界即可實現波浪的穩定流動，且波浪的穩定不需要時間，非常適合航行體高速入水工況的計算。因此，本文在三維波浪數值水池的邊界處理中，對波浪的入口和出口區域采用了周期性邊界技術，如圖1所示。

當流體粒子流出計算域并進入右側的出口區域時，粒子攜帶著所有的物理信息，立刻轉移到流體區域的最左側，作為計算域的流入粒子。出口區域和入口區域的虛粒子由流體域兩側的粒子復制生成，作為計算域的邊界條件。采用周期性邊界后，可以模擬波浪的穩定流動，出口邊界和入口邊界的流量可以保持守恒。采用周期性邊界的波浪數值水池模擬結果如圖2所示，可以看出施加周期性邊界之后，經過一段時間的運動，波形和波浪壓力分布依然保持穩定。

圖2 波浪的壓力分布Fig. 2 Pressure distribution of waves

為了研究計算域大小對于施加周期性邊界的數值水池的影響，本文對不同計算域的波浪水池進行了模擬。標準波浪水池長度為2L= 3.12 m，寬度為D= 0.6 m，然后建立4L×D和2L× 2D的波浪水池，得到不同計算域下波浪水池的速度場模擬結果，如圖3所示。從圖3中可以看出，不同計算域波浪水池的速度場在同一時刻保持一致，證明了計算域的大小對于波浪水池的影響很小。同時速度場也與線性波的理論速度場保持一致，證明了采用周期性邊界的波浪數值水池的有效性。為了提高計算效率，本研究中的波浪數值水池主要采取2L×D的計算域。

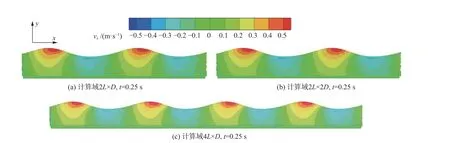
圖3 不同計算域下波浪的速度分布Fig. 3 Velocity of waves in different computational domains

1.4 四元數方法

流體-剛體耦合運動問題中，涉及到兩種坐標系，分別為以大地為基準的慣性坐標系（也稱固地坐標系）和以運動剛體為基準的非慣性坐標系（也稱隨體坐標系）。隨體坐標系的坐標原點Ob位于物體質心處，如圖4所示。本文中流體流動和剛體的平動在固地坐標系中計算，但是剛體的轉動角速度和角加速度在隨體坐標系中進行計算。

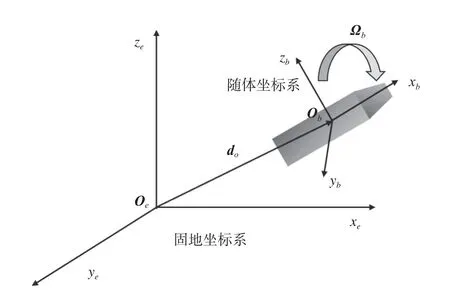
圖4 坐標系轉化示意圖Fig. 4 Schematic of coordinate system transformation

航行體在波浪中的運動軌跡非常復雜，涉及到六自由度的運動響應。傳統的六自由度運動計算往往是基于歐拉角法，但歐拉角法在計算隨體坐標系和固地坐標系之間角速度的轉化時，角速度變換矩陣中存在著奇異值，這會導致歐拉角法在計算剛體翻轉過程中出現誤差。四元數法相對于傳統的歐拉角法，其角速度和四元數之間的變換矩陣中不存在奇異值，可以適應不同姿態下剛體六自由度運動的計算，在剛體翻轉情況下的計算精度更高[34]。因此，本研究中采用四元數法來計算剛體的六自由度運動。

在數值水池中，剛體在固地坐標系中的物體合力Fe和力矩Te可根據下列公式[12]得到：

其中，do為連體坐標系中物體的質心坐標。初始四元數[q0q1q2q3]T是由初始歐拉角Θe=[αβγ]T得到[17]，轉換關系如下：

四元數構建坐標系轉換矩陣R表達式為[17]：

隨體坐標系下的力矩Tb和合力Fb可通過轉換矩陣R得到[35]，具體公式如下：

質心加速度和轉動角加速度公式[35]如下：

式中：M為物體質量，Ib為相對質心Ob的轉動慣量矩陣。通過時間步積分可以得到隨體坐標系下的質心速度Ub和轉動角速度?b，以及每個粒子在隨體坐標系下的速度vb, j和加速度ab, j[35]：

固地坐標系下的質心速度Ue和轉動角速度?e的計算[35]可根據以下公式：

Q為隨體坐標系下角速度和固地坐標系下四元數變化率之間的轉換矩陣[17]，表達式為：

從公式（13）中可以看出，隨體坐標系中角速度到固地坐標系四元數變化率的轉化矩陣中不存在奇異值，適合任何姿態的計算。在得到四元數變化率后，通過時間步積分可以更新四元數，進而更新轉換矩陣R。固地坐標系下的粒子位置和速度信息也可以實時更新[35]，具體公式如下：

四元數的完整計算流程如圖5所示。

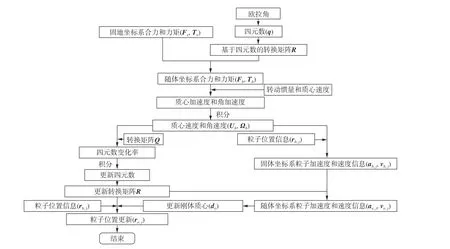
圖5 四元數法流程Fig. 5 Flow chart of the Quaternion method

1.5 六自由度運動計算驗證

為了驗證基于四元數法的六自由度運動計算精度，本文同時采用自主編制的SPH程序和基于有限體積法（finite volume method, FVM）的成熟商業軟件STAR-CCM+，對方塊體六自由度落水過程進行模擬，通過SPH與FVM結果對比，驗證方塊體六自由度運動的數值計算精度。

方塊體落水示意圖如圖6所示。方塊體長度為128 mm、寬度為68 mm、厚度為4 mm，質量為0.2184 kg，質心距方塊體底部65.2 mm、距離水面67.2 mm，方塊體連續繞y軸和z軸旋轉25°，轉動慣量Ix、Iy、Iz分別為0.00039676 、0.00009、0.0003082 kg·m2。

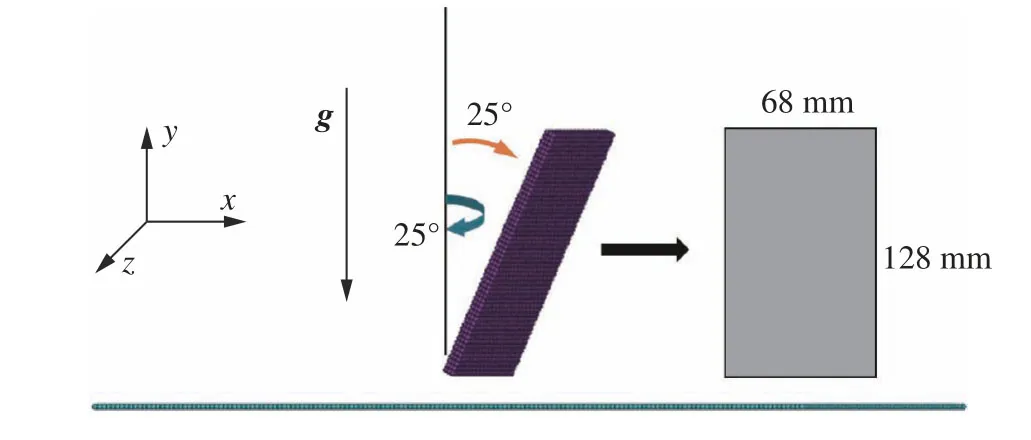
圖6 方塊體落水示意圖Fig. 6 Schematic of a cuboid falling into water

圖7為采用SPH和FVM方法對方塊體落水過程的模擬結果，方塊體落水的速度變化曲線如圖8所示。可以看到，基于四元數法的SPH方法模擬結果與FVM的模擬結果吻合得很好。

圖7 方塊體落水的SPH和FVM模擬結果Fig. 7 SPH and FVM simulation results of a cuboid falling into water

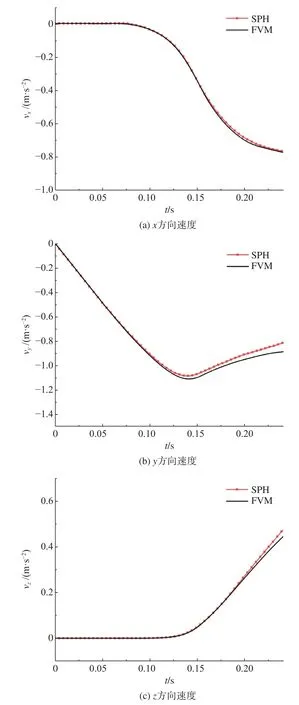
圖8 方塊體落水的的速度曲線Fig. 8 Velocity curve of a cuboid falling into water

2 航行體數值模型建立與驗證

為了更好地與文獻結果進行對比驗證，本文以楊曉光等開展的高速航行體斜入水研究[19]為參考，選用相同的工況條件進行計算。航行體質量為1.35 kg，質心距前端面為123 mm，轉動慣量Ix、Iy、Iz分別為0.00059、0.005186、0.005186 kg·m2。航行體幾何示意圖如圖9所示。平靜水面下的航行體入水數值模型見圖10。為了降低計算規模，提高計算效率，同時保證剛體周圍流場的模擬更為精細，本文使用了多分辨率技術[36]，加密區域粒子隨剛體的運動動態加密，如圖10（b）所示。

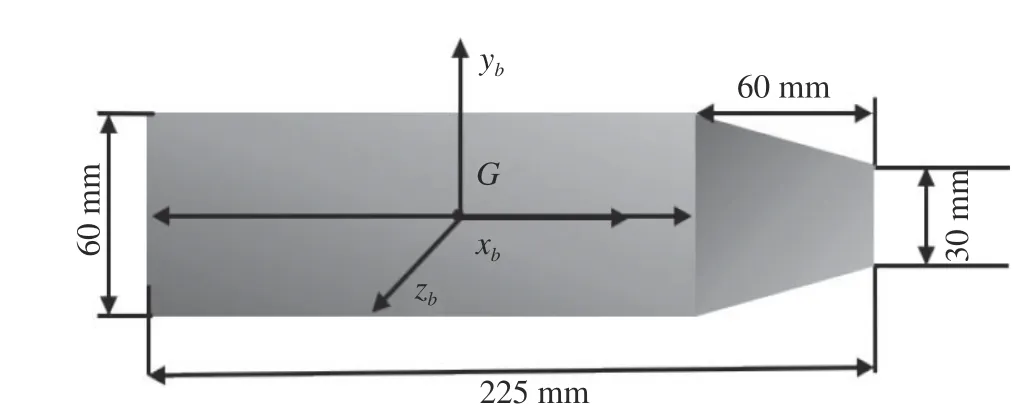
圖9 航行體幾何示意圖Fig. 9 Geometric diagram of the projectile

在進行數值模擬之前，首先進行粒子間距的收斂性分析。選擇粒子間距分別為10.0、5.0、2.5 mm，計算得到3種不同粒子間距下y方向航行體的加速度ay變化曲線，見圖11。當粒子間距小于5 mm時，計算結果趨近于收斂。因此，為了提高計算效率，在后續算例中采用5 mm的粒子間距。

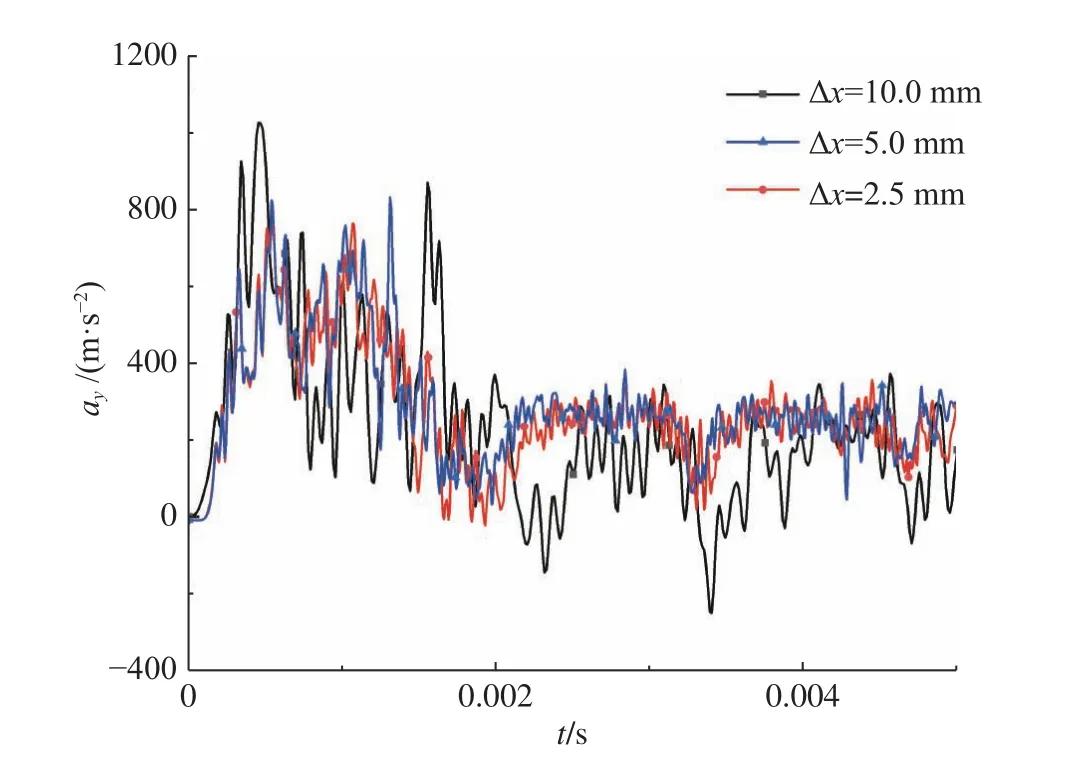
圖11 不同粒子間距下的y方向航行體加速度Fig. 11 The y-direction accelerations of the projectile with different particle sizes

隨后，通過在靜水狀態下的航行體高速入水模擬來驗證本文SPH方法的可行性。文獻[19]的航行體高速入水試驗在靜水狀態下開展，航行體入水速度為60 m/s，入水傾角為20°。本文針對相同工況開展了數值模擬研究，從軸向加速度aA對比結果圖12可見，SPH方法的模擬結果與試驗結果吻合得很好，驗證了本文SPH模型對航行體入水沖擊載荷的預報精度。

圖12 SPH方法航行體軸向加速度和試驗結果[19]的對比Fig. 12 Comparison of the axial acceleration of the projectile between SPH simulation results and experimental results[19]

同時，在文獻[19]中楊曉光等也采用了網格類CFD方法對靜水工況下的航行體入水進行了模擬。本文針對相同工況，開展了無網格數值模擬研究。SPH方法與網格法在不同時刻的模擬結果對比如圖13所示，可以看出，SPH方法預報的彈體運動和自由面變形情況均與文獻結果吻合良好。此外，SPH結果中捕捉到了更為顯著的液滴飛濺，凸顯了無網格算法捕捉自由液面大變形的優勢。

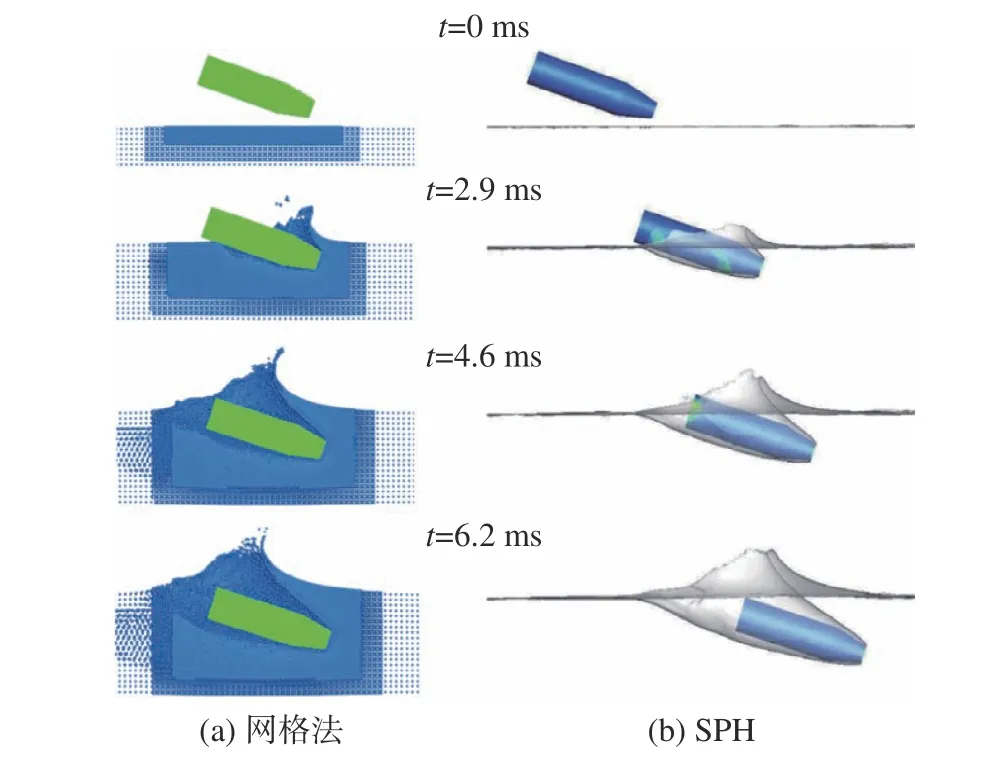
圖13 SPH方法航行體入水模擬結果和文獻結果[19]的對比Fig. 13 Comparison of water-entry simulation results of the projectile between SPH method and Ref.[19]

3 波浪環境下的航行體入水模擬

在波浪環境下航行體入水的SPH模擬中，波浪參數設置與楊曉光等[19]的數值模型一致。波浪周期T為1 s，波高H為0.15 m。在0.6 m的水深下，波長L為1.56 m。數值水池計算域長度為3.12 m，為兩倍波長，寬度D為0.6 m。

航行體以與水平面20° 的傾角、60 m/s的速度入水，選擇4個波浪相位點入水展開數值模擬，分別為0°、90°、180°和270°，入水點如圖14所示。航行體的質心與對應相位點的連線與水平面成20° 的傾角。

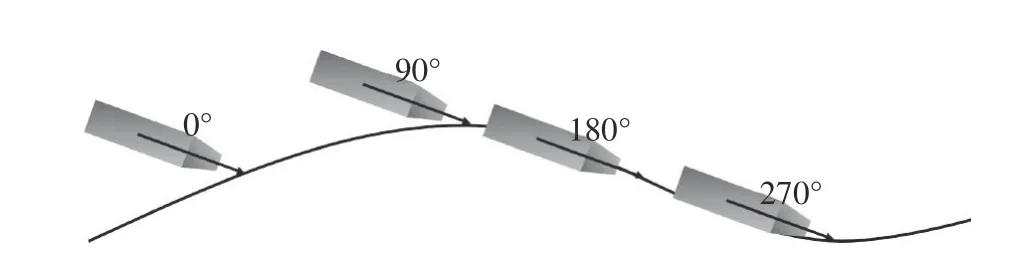
圖14 航行體入水位置的波浪相位角Fig. 14 Wave phase angles at the entry position of the projectile

3.1 不同相位角的模擬結果

航行體在波浪90° 和270° 相位角入水的模擬結果如圖15所示。

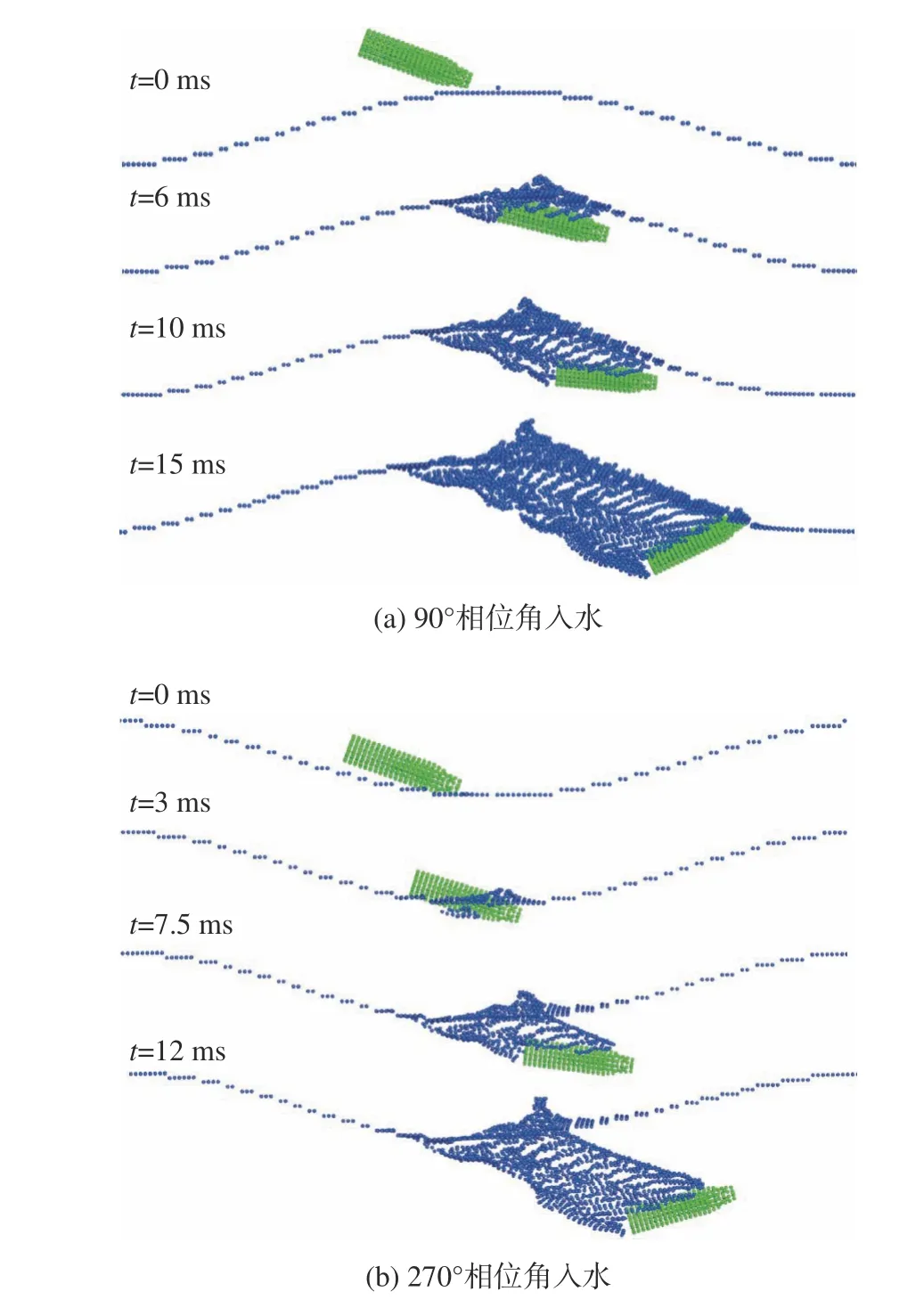
圖15 航行體入水過程的SPH模擬結果Fig. 15 SPH simulation results of the projectile in the waterentry process

從圖15中可以看出，航行體在入水后姿態角發生偏轉，頭部上揚，在90° 的相位角入水工況中，入水15 ms后航行體開始沖出水面。圖16給出了與楊曉光等[19]采用網格類方法結果的對比，可以看出本研究的SPH模擬結果與網格類方法的模擬結果非常吻合。其中，航行體在0° 相位角入水的模擬結果與靜水狀態下入水結果類似；而航行體在180° 相位角入水過程中，發生翻轉，頭部上揚，航行體沖出水面。兩個相位角下航行體入水的SPH模擬結果與網格法模擬的航行體運動軌跡非常吻合。除此之外，得益于SPH粒子法的無網格和拉格朗日特性，可以自動構建自由液面，因此本研究能夠精確高效捕捉航行體入水時飛濺液滴的形態和軌跡，如圖15和圖16所示。而網格類CFD方法在處理液面大變形和液滴飛濺時，需要采用Level Set或者流體體積（volume of fluid,VOF）技術進行自由液面追蹤，且追蹤精度受網格分辨率影響極大。圖16右側展示的網格法計算結果中，受網格尺寸限制，未能精確捕捉到液滴飛濺形態。

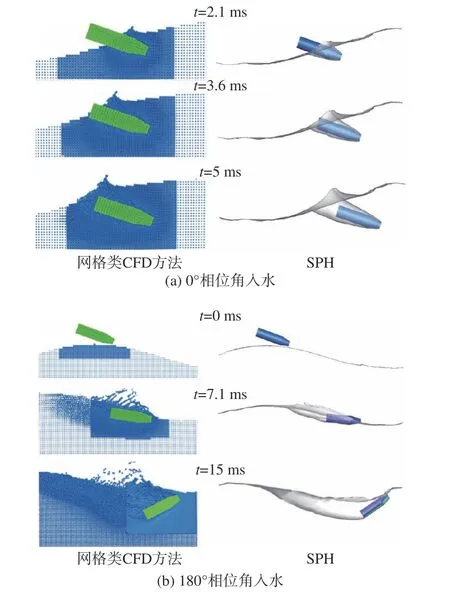
圖16 航行體入水過程的SPH模擬結果與參考結果[19]對比Fig. 16 The comparison between SPH simulation results and Ref.[19] of the projectile in the water-entry process

3.2 不同相位角對于航行體運動軌跡的影響

為了定量分析不同相位角下航行體的入水狀態和軌跡，提取了不同相位角下航行體入水后的轉動角度和運動速度數據，變化曲線如圖17所示。

圖17 不同相位角下航行體入水速度和角度變化Fig. 17 The velocity and angle curves of the projectile with different phase angles

從圖17可知：4個相位角下、入水15 ms時，航行體傾斜角度全都從-20°變為正值，都呈現出頭部上揚的姿態；在270° 相位角下，航行體在入水后的翻轉速度最快，而在0° 相位角下航行體翻轉速度最慢，所以270° 相位角下航行體的x和y方向速度衰減最快，0° 相位角下航行體y方向速度衰減最慢；而在180°相位角下，航行體入水后半浮于水面上，所以在x方向上速度衰減最慢。

由于本研究中航行體入水的速度較大，波浪流動速度的影響相對較小，相對于靜水條件下的航行體入水，波浪對于航行體入水軌跡的影響主要體現在不同相位角入水對于航行體實際入水角度的改變以及波浪形狀對于航行體出水時刻的影響。本文模擬的4種相位角入水工況中，根據圖15和圖16的模擬結果可知，0° 相位角下的航行體與水面的夾角最大，水動力載荷主要集中在軸向，側向載荷相對較小，因此轉動速度最慢，在y方向上的速度衰減最慢，彈道穩定性方面表現最好；而180° 相位角下的航行體與水面的角度很小，航行體幾乎是懸浮在水面上，側向載荷較大，因此轉動角度較快，航行體也迅速出水，由于航行體半浮于水面，受到的水阻力較小，所以在x方向上的衰減更慢；而在270° 相位角下，航行體的入水角度與波面幾乎平行，所以側向載荷較大，轉動速度最快，但入水后航行體進入到另一個波浪的波峰區域中，距離波面較遠，出水時刻更為滯后，同時入水后的迅速轉動也導致水阻力增大，所以在x和y方向的速度衰減最為明顯。靜水條件下的航行體入水軌跡發展主要受入水角度影響，而波浪條件下航行體入水軌跡受入水角度、波浪相位角和波浪形狀的多重影響，更為復雜。

4 結論

基于SPH方法，本文提出一種新型周期性波浪邊界技術并建立了波浪環境下的數值水池，簡化了傳統推板造波過程中的繁瑣處理，可以迅速準確地生成具有穩定周期和波形的波浪。同時，將四元數法植入到SPH計算框架，消除了傳統歐拉角法中奇異值導致的誤差，實現了對物體入水后六自由度運動的精確模擬。

通過對航行體高速入水過程的模擬，SPH模擬結果與參考文獻中的實驗結果及網格類CFD方法模擬結果吻合良好，且SPH方法能精確捕捉液滴飛濺的細節。對不同波浪相位角下航行體入水后的姿態變化的分析表明，波浪相位角會明顯影響航行體的入水運動軌跡，0° 相位角入水在保持彈道穩定性方面表現最優。

本研究中采用單相流模型和線性波理論，未考慮空氣效應，也未對航行體高速入水過程中的空化現象進行模擬，所以本研究模擬的是線性波條件下的不考慮氣穴效應的航行體入水問題。在未來研究中，擬開發SPH空化模型，采用多相流SPH模型開展計算，對入水彈道軌跡以及空泡演化進行更深入的力學機理分析。