雙Λ 超核同位旋標量巨共振性質的相對論研究*

溫靜 孫帥 曹李剛 張豐收3)?

1) (北京師范大學核科學與技術學院,射線束技術教育部重點實驗室,北京 100875)

2) (北京市科學技術研究院,輻射技術研究所,北京 100875)

3) (蘭州重離子加速器國家實驗室,原子核理論研究中心,蘭州 730000)

基于相對論平均場理論(RMF),采用TM1 以及有效超子?核子和超子?超子相互作用,首先研究了16O 和 的單粒子能級受超子的影響情況,發現超子的加入使得核子能級能量降低.其次基于相對論無規位相近似方法(RRPA),自洽地計算了16O和 同位旋標量巨單極和四極共振態.發現相比于16O 各巨共振的響應函數,超核的響應函數會發生改變.研究表明: 這種改變主要來自于超子的加入導致的核子單粒子能級的改變,以及超子粒子?空穴組態躍遷的貢獻,而超子?超子剩余相互作用對單極和四極共振在低能區的響應函數的影響比較小,特別對高能區的響應函數基本沒有影響.

1 引言

1953年,波蘭科學家Danysz 和Pniewski[1]首次在宇宙射線中發現 Λ 超核,揭示了原子核中除中子和質子外,還可能包含 Λ 超子,自此人們開始對超核性質進行研究,超核物理成為核物理研究的一個重要分支.由于超子在真空中的壽命很短,因此很難通過超子–核子或者超子–超子散射實驗來獲得它們之間的相互作用信息.與質子和中子不一樣,作為奇異粒子,超子并不受Pauli 原理的限制,因此它可以深入到原子核的內部而形成超核,為人們研究超核中的相互作用信息提供了條件,是了解超子–核子和超子–超子相互作用的理想場所.自從首次發現超核以來,在實驗室中通過不同的反應機制產生超核方面的研究取得了顯著進展,如通過強子引起的反應,用高能光子或電子轟擊原子核產生超核,以及高能重離子碰撞的碎裂反應等.最近,STAR 合作組織在相對論重離子碰撞中還發現了反物質超核,并首次測量它們的結合能[2].隨著世界上高強度高能量加速器的建立,例如德國的PANDA、日本的J-PARC 以及中國的HIAF 裝置等[3–5],越來越多的超核將被產生出來,超核物理將有可能擴展到豐中子或豐質子超核、多奇異超核、反物質超核和具有奇異性的高密度強子物質等[6,7].實驗上超子–核子相互作用主要通過單 Λ超核的γ能譜來研究[8].由于 Λ 粒子的加入,原子核的一些性質將發生變化,如激發能和γ射線的躍遷概率,這些變化揭示了 Λ 超子的雜質效應.精確地約束超子–核子相互作用,需要更多更豐富的實驗數據,各大實驗室計劃采用新的探測器陣列對單 Λ 超核的γ能譜進行詳細研究,旨在獲得關于sd 殼層區域超核的低能級的新數據,這將有助于進一步了解超核中的相互作用.

理論上,為了能夠很好地描述超核性質,已經提出和發展了許多理論類型,包括采用唯象超子–核子相互作用和采用更微觀的超子–核子相互作用的理論方法,如Skyrme 有效相互作用、相對論有效相互作用、Nijmegen 微觀的軟核芯和擴展的軟核芯相互作用以及微觀的手征相互作用等[9–15].它們被廣泛用于適當的核多體理論來研究超核的各種性質,如殼層模型、團簇模型、反對稱分子動力學模型、非相對論和相對論平均場模型等[16–31],這些理論模型對超核的基態性質、單粒子能級的性質、超核收縮、超核變形、裂變勢壘高度、勢能面和中子滴線的延伸等做了詳細的研究.除了單 Λ 超核外,實驗和理論上還對雙 Λ 超核的性質進行了研究.實驗上也是通過觀察雙 Λ 超核發射的γ能譜來推斷出有關核子–超子以及超子–超子相互作用的信息.然而,到目前為止,在核乳膠實驗中觀察到的雙 Λ 超核實驗數據很稀少.另外,理論研究認為相對論重離子碰撞可以產生豐富的多奇異原子核,反質子引起的兩步核反應過程也是多奇異超核產生的有效機制[32,33],這為未來國內外的超核實驗研究裝置提供了理論依據.HIAF 裝置是中國正在建造的新一代強流離子加速器,計劃于2025 年建成投入使用,超核物理是HIAF 裝置重要的研究目標之一,將開展超核的產生以及譜學方面的研究[5].因此,系統的理論計算對研究雙 Λ 超核中的 超子雜質效應很有幫助,也是未來實驗上產生雙 超核建議合適的靶核的有力工具.

為了系統地研究從輕核到重核的雜質效應,平均場理論以及無規位相近似方法提供了最合適的工具之一.這種方法已經應用于研究整個核素圖中正常核的集體激發態性質,獲得了重要的進展[34–47].采用Skyrme HF 理論以及無規位相近似方法,文獻[48,49]研究了雙 Λ 超核的集體激發性質,討論了雙 Λ 超子雜質效應對原子核集體激發響應方程以及能量的影響.而基于相對論核多體理論的相關研究還沒有被報道過.本文將相對論平均場以及無規位相近似方法推廣到雙 Λ 超核的單粒子能級和集體激發態性質的研究中.選擇雙 Λ 超核作為研究對象,部分原因是在雙 Λ 超核中時間反演對稱性的描述比較簡單.另外,預計雙 Λ 超核中的雜質效應更強,這樣的計算將提供單 Λ 超核雜質效應的上限.

2 理論模型

相對論平均場理論是基于介子交換有效場論和能量密度泛函發展起來的理論,又稱相對論協變密度泛函理論[50].由于具有場論基礎和可自動給出原子核自旋–軌道劈裂等優勢,相對論平均場理論在原子核性質計算中得到了廣泛應用.近年來,相對論平均場理論得到了不斷完善和發展,成功地描述了原子核的均方根半徑、質量、中子和質子分離能、自旋對稱等性質[51–62].關于描述超核基態性質的相對論平均場理論可以參考文獻[21–27],本文給出簡要的介紹.描述由核子、超子和介子組成的核多體束縛系統的拉氏量密度為

其中,ψB和ψΛ是核子和超子 場算符;MN和MΛ為核子和超子的裸質量;mσ,mω,mρ,mσ?和m?分別是 σ,ω,ρ,σ?和?介子的質量;gσ,gω,gρ和分別是介子與核子、超子的耦合常數;g2,g3和c3為介子的自耦合常 數;是ω-Λ 的張量耦合系數;A是電磁場,它只作用于質子上,由于超子是電中性和同位旋標量粒子,所以它不與電磁場耦合.ω,ρ和?介子以及電磁場的張量形式分別表示為

在球形近似下,可以得到核子的徑向Dirac 方程為

其中,S(r)=–gσσ(r) 表示核子相互作用的標量勢,V(r)=表示核子相互作用的矢量勢.

超子的徑向Dirac 方程為

其中,SΛ(r)=是超子相互作用的標量勢,VΛ(r)=是超子相互作用的矢量勢.通過自洽求解方程(3)和方程(4)以及介子場和電磁場方程,可以獲得核子以及超子的單粒子能和單粒子波函數等基態性質.

基于原子核的基態,自洽的相對論無規位相近似方法(RRPA)已經建立起來,它被用于描述有限核的各種集體激發性質.相對論無規位相近似方法的發展包括兩個重要的階段: 一方面在相對論無規位相近似方法計算中考慮了具有非線性自相互作用的介子傳播子,這樣可以合理地描述原子核的不可壓縮性,再現重核中同位旋標量巨單極共振的實驗數據;另一方面,在相對論無規位相近似方法中對負能海態貢獻的自洽處理[34,35],建立了完全自洽的相對論無規位相近似方法.

本文將擴展相對論無規位相近似方法,使之能夠描述雙 Λ 超核的集體激發性質.根據線性響應理論,一個量子體系對外場算符P的響應函數是其關聯極化算符的虛部,公式如下:

其中,P為外場算符;k,k′為轉移動量;E為激發能量.

關聯極化算符可以通過求解Bethe-Salpeter方程得到:

其中,求和指標i表示 σ,ω,ρ,σ?,?介子以及光子;gi和Di表示相應介子和光子的耦合常數和傳播子.在非線性模型中介子的傳播子在動量表象下不再是一個簡單的定域形式,它可以用數值方法求解非定域方程得到[63].Γi為相互作用頂角函數,對于 σ 和σ?介子,Γi=1,對于 ω和?介子以及光子,Γi=γμ,對于 ρ介子,Γi=γμτ3.Π0代表非微擾關聯極化算符.

對于每個確定的角動量L,非微擾關聯極化算符為

其中,a和A分別代表核子(超子)占有和不占有費米海態;代表核子(超子)負能Dirac 海態;fa和fA分別代表核子(超子)占有和不占有費米海態波函數;代表核子(超子)負能Dirac 海態波函數;Ea,EA和為相應單粒子態的能量.

3 結果與討論

3.1 16O和 單粒子能級

在研究超核的激發態性質之前,首先使用相對論平均場理論進行原子核基態性質的計算,研究超子對原子核單粒子能級的影響,計算中雙 Λ 超核采用球形對稱近似.基于TM1 參數計算了的單粒子能級,將得到的單粒子能級和普通核16O 的單粒子能級進行比較.圖1 是相對論平均場計算得到的16O和的中子、質子以及超子的單粒子能級,黑色實線表示普通核16O 的單粒子能級,紅色虛線表示超核中中子、質子和超子的單粒子能級.從圖中可以看出,由于超子的加入,在超核中中子和質子單粒子能級低于16O 中的相應能級,這是由于超子–核子的相互吸引作用,使得質子和中子的中心勢場加深,從而計算得到的單粒子能級變得更加束縛,并且發現 Λ 超子的加入對質子和中子能級1s 態的影響最大.

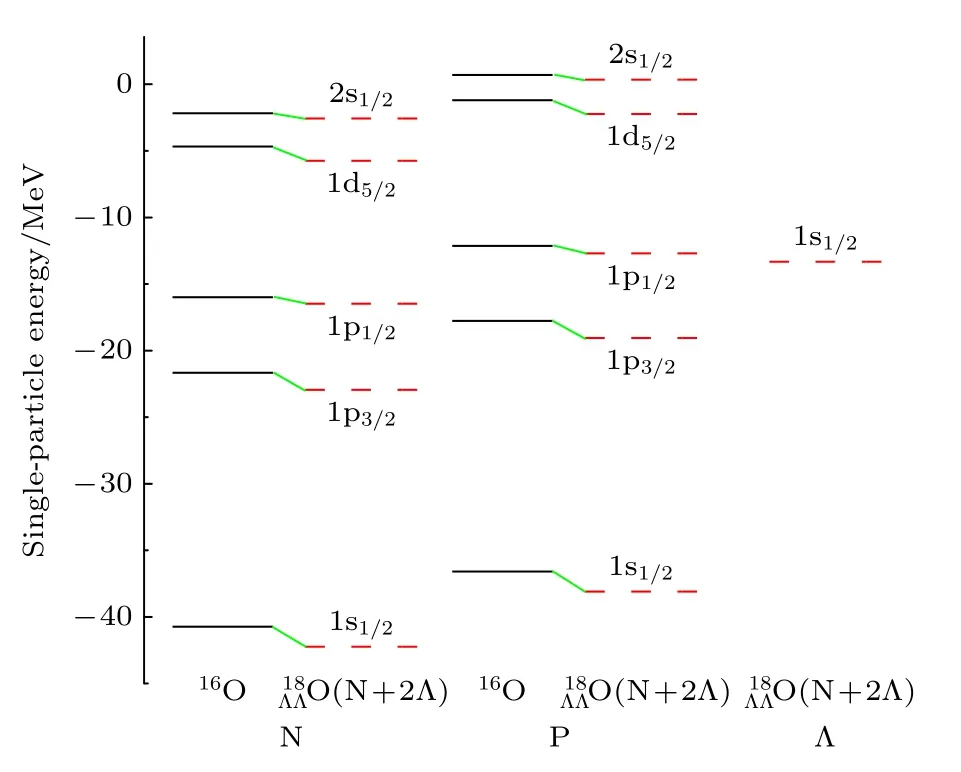
圖1 中子、質子和超子的單粒子能級.黑色實線為16O 的單粒子能級,紅色虛線為 的核子和超子單粒子能級Fig.1.Single-particle energies of neutrons,protons,and Lambda hyperons.Energy levels of 16O are denoted by black solid lines while those of are denoted by red dashed lines.

表2 給出計算得到的16O和核芯的質子、中子的單粒子能級和能級差,?ε代表的是普通核與超核之間相應單粒子能級之差.從表2 可以看出,由于超子的加入,超子–核子與超子–超子之間的相互作用使質子和中子平均場的中心部分加深,超核中核子的單粒子能級低于普通原子核中相應的單粒子能級.超子的影響對于能量比較低的1s1/2態比較大,隨著能級靠近費米面,單粒子能級的差值?ε也逐漸減少.另外,單粒子能級的差值也有可能受到軌道角動量的影響,如中,質子和中子1d5/2態的單粒子能級差比相鄰的1p1/2態的單粒子能級差要大.由于超子的加入,原子核單粒子能級的變化有可能會引起原子核集體激發態性質的變化.

表1 TM1 參數,核子以及介子質量的單位為MeVTable 1.Parameter sets TM1,and the masses of nucleons and mesons are given in MeV.

表2 使用相對論平均場模型計算得到的 16 O 和 中質子、中子的單粒子能級(ε),?ε 表示普通核與超核之間的相應能級差 (單位為MeV)Table 2.Single-particle energies of neutrons and protons in 16 O and the results are obtained by using the RMF model.?ε is the difference of corresponding level in normal nucleus and hypernucleus (unit in MeV).

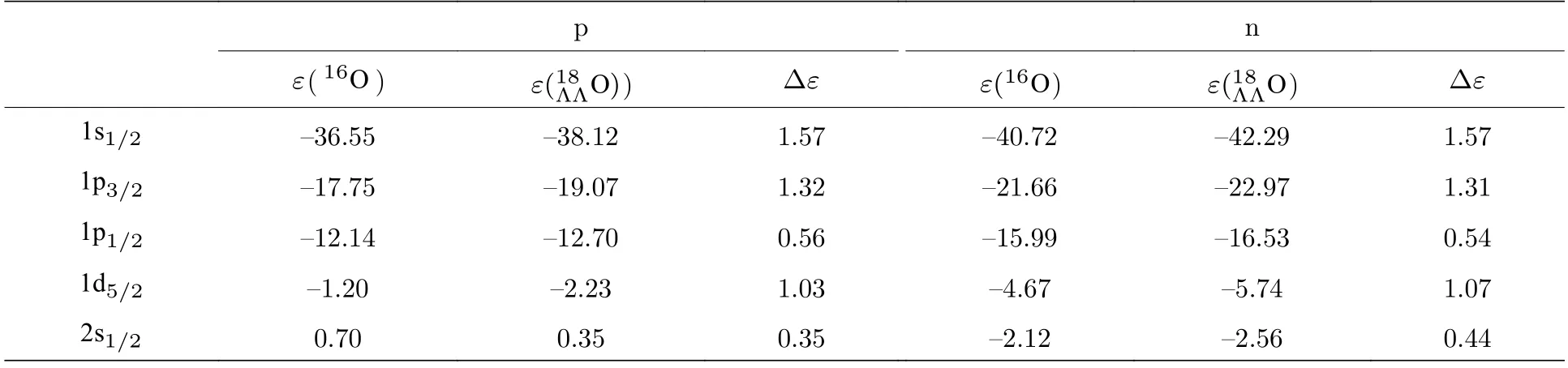
表2 使用相對論平均場模型計算得到的 16 O 和 中質子、中子的單粒子能級(ε),?ε 表示普通核與超核之間的相應能級差 (單位為MeV)Table 2.Single-particle energies of neutrons and protons in 16 O and the results are obtained by using the RMF model.?ε is the difference of corresponding level in normal nucleus and hypernucleus (unit in MeV).

在原子核的基態之上,基于相對論無規位相近似理論,以16O和為例,研究超核的同位旋標量單極和四極巨共振性質,討論超子在原子核集體激發態性質中的雜質效應.

同位旋標量巨單極共振是一種常見的壓縮模式,也被稱為核的呼吸模式,被用于提取核物質不可壓縮性系數.同位旋標量巨單極共振對應的外場算符形式是:

圖2(a)給出了16O 與單極共振的非微擾(Hartree)響應的計算結果,黑色實線表示16O 的結果,紅色虛線表示的結果.在16O 的Hartree響應中,為方便研究,將其分成3 個能區來討論,分別是: 低能區(0—21 MeV),中能區(21—35 MeV)和高能區(35 MeV 以上).低能區主要有2 個單粒子共振峰,分別位于17.52 和19.54 MeV,它們由質子和中子(2p1/2,組態所貢獻.中能區響應函數由多個粒子–空穴組態共同貢獻,位于22.54和24.63 MeV 的共振峰分別由質子和中子組態(2p3/2,)所貢獻,而27.30 MeV 的峰由中子組態(3p1/2,) 貢獻,29.44 以及31.24 MeV 兩個共振峰分別由質子和中子組態(3p3/2,) 貢獻.高能區主要由3 個粒子–空穴激發形成,分別位于38.50 MeV (主要由質子與中子組態(2s1/2,)貢獻)、40.80 MeV (主要由質子組態(4p3/2,)貢獻)和42.50 MeV (主要由中子組態(4p3/2,)貢獻.對于單極共振的Hartree 響應函數,最明顯的變化是低能區的單粒子共振峰變得更強,這種變化主要來自于超子的組態(2s1/2,) 的躍遷,共振峰的能量為18.53 MeV.另外,中能區和高能區的共振峰也由于超子的加入而向高能方向移動,這主要是因為超子–核子及超子–超子相互吸引作用使核子平均場的束縛性更強,而這種束縛性對于費米面以下的空穴態的能量影響較強,對于費米面以上的粒子態的能量影響較弱,這導致Hartree響應中粒子態與空穴態之間的能量差(εp-εh)相比于不加超子時的情形變大,因此對應的共振峰會向高能方向移動.

圖2 16O和 同位旋 標量巨 單極共 振響應函數(a) Hartree 響應函數;(b) RRPA 響應函數Fig.2.Response functions of isoscalar monopole resonance for 16O and : (a) Hartree response;(b) RRPA response.

圖2(b)給出了16O 與的單極RRPA 響應函數分布,其中,黑色實線表示16O 的RRPA 響應函數,綠色點線與紅色虛線表示的RRPA 響應函數,綠色點線為在RRPA 計算中未包含超子–超子剩余相互作用,而紅色虛線對應的結果則包含了所有的剩余相互作用,是一種完全自洽的計算.對比16O(黑色實線)與(紅色虛線)的RRPA響應函數,可以發現低能區的RRPA 響應強度明顯增強,中高能區的共振峰向較高能區移動.此外,可以發現綠色點線與紅色虛線在低能區有可見的差別,而在其他能區差別不大,這說明超子–超子剩余相互作用對于單極RRPA 響應的影響比較微弱.因此,在單極共振的RRPA 響應中,16O 與的差別主要來自于Hartree 響應中能量的改變以及超子組態(2s1/2,) 躍遷的貢獻.

接著來研究超子在原子核16O與同位旋標量巨四極共振中的影響,其對應的外場算符形式為

圖3(b)給出16O 與的四極共振的RRPA響應函數分布.其中,黑色實線表示16O 的RRPA響應,綠色點線與紅色虛線表示的RRPA 響應,綠色點線表示在RRPA 計算中未包含超子–超子剩余相互作用,而紅色虛線對應的結果則包含了所有的剩余相互作用,是一種完全自洽的計算.對比(紅色虛線)與16O(黑色實線)的RRPA 響應,可以發現當考慮了超子的貢獻之后,主峰向高能方向移動,其峰強略有提高;15—20 MeV 能區的響應強度相對于16O 的結果也有明顯提升,這主要是由于兩個超子粒子–空穴組態的貢獻.此外,發現綠色點線與紅色虛線在低能區和主共振區有細微的差別,在其他能區幾乎重合,這說明超子–超子剩余相互作用在巨四極共振響應強度分布中的作用比較小.綜上所述:16O 與四極共振的RRPA響應函數的差別主要來自于Hartree 響應中粒子–空穴能量的改變以及超子組態(1d5/2,)和(1d3/2,) 的貢獻.

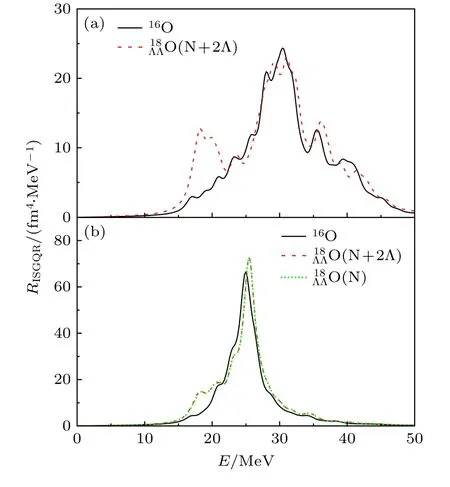
圖3 16O 和 的同位旋標量巨 四極共 振響應函數(a) Hartree 響應函數;(b) RRPA 響應函數Fig.3.Response functions of isoscalar quadrupole resonance for 16O and : (a) Hartree response;(b) RRPA response.

4 結論

基于相對論平均場和相對論無規位相近似理論,本文研究了16O與的單粒子能級和集體激發態性質,討論超子在這些性質中的雜質效應.計算結果表明: 超子的加入導致單粒子能的減小,這是因為超子–核子、超子–超子的吸引相互作用加強了核子平均場的束縛性.發現超子的雜質效應對于不同的能級影響也不同,一般而言,它對于1s1/2態的影響最大,對費米面附近的單粒子能級影響較小,也具有軌道角動量依賴性.研究了16O 和的同位旋標量巨單極和四極共振的Hartree 和RRPA 響應函數,對貢獻到各主要共振峰的組態進行了詳細分析,并探討了超子的加入對Hartree 和RRPA 響應函數的影響.分析表明,響應方程的改變主要來自因加入超子引起的核子單粒子能級的改變及超子組態躍遷的貢獻,發現超子–超子剩余相互作用對單極和四極共振在低能區的響應函數有一定影響,對高能區的響應函數的影響可忽略.