結合源偏倚和權窗的蒙特卡羅全局減方差方法*

張顯 劉仕倡 魏軍俠 李樹 王鑫3) 上官丹驊

1) (北京應用物理與計算數學研究所,北京 100094)

2) (華北電力大學核科學與工程學院,北京 102206)

3) (中國工程物理研究院高性能數值模擬軟件中心,北京 100088)

全局計數問題在反應堆pin-by-pin 模型蒙特卡羅模擬和多物理耦合計算中動態粒子輸運蒙特卡羅模擬等重大研究領域中都有廣泛的應用場景.大量的全局減方差算法研究立足于全局計數誤差分布的展平,由此提高全局計數的整體效率.本工作針對兩種高效全局減方差算法,即均勻計數密度算法(屬于源偏倚算法的一種)和權窗算法的結合展開研究,提出利用均勻計數密度算法的偏倚因子調整權窗下限,由此實現兩種算法的有機結合.基于Hoogenboom-Martin 壓水堆全堆基準題中開展了一系列對比測試,驗證了混合全局減方差算法更優于單一權窗算法或均勻計數密度算法,尤其是在降低最大誤差方面.同時,基于新的指標,驗證了均勻計數密度算法較經典的均勻裂變源算法具有更好的表現.研究結果表明,本文提出的混合全局減方差算法能高效求解全局計數問題,進一步促進了相關領域的研究.

1 引言

蒙特卡羅(Monte Carlo,MC)方法具有幾何建模能力強、物理過程描述高保真等優點,被廣泛應用于定態和動態粒子輸運問題的模擬.隨著研究的深入,輸運問題的幾何模型愈加精細,考慮的因素越來越多,例如反應堆pin-by-pin 模型[1,2]和多物理耦合計算中大規模動態粒子輸運模型等[3].龐大的幾何和計數規模以及高效高精度的計算需求,給MC 粒子輸運模擬帶來巨大挑戰.由于所模擬系統的空間不均勻性,計數統計誤差在全局范圍內呈現不均勻分布,由此帶來整體效率的低下.解決這一問題的本質困難在于高功率區域因具有較多的粒子樣本數,能較快獲得統計收斂的結果,而低功率區域的收斂則耗時巨大,僅單純增加樣本總數,只會導致絕大部分計算資源浪費在已收斂的高功率區域,難以(在有些情況下是不可能的)獲得全局收斂的計數結果,而這些結果對于反應堆計算或高置信度多物理耦合計算至關重要.

為實現全局計數整體誤差分布的展平,需要引入相關的全局減方差算法指導MC 粒子輸運,提高全局計數的整體效率[4,5].均勻裂變源(UFS)算法[6–8]是針對臨界計算提出的一種高效全局減方差算法,根據裂變中子源的密度分布重新分配裂變源,以便在低功率區域人為地產生更多的裂變中子.基于UFS 算法的啟發,均勻計數密度(UTD)算法[9]被提出,其利用目標計數密度來指導源粒子的偏倚,獲得了更高的全局減方差性能.此外,權窗(WW)算法[10,11]也是一種被廣泛應用的全局減方差算法,不同于UTD 和UFS 算法,WW 算法是對粒子的輸運過程進行偏倚,以引導粒子輸運到更廣泛的區域.

為進一步提高MC 臨界計算全局計數問題的整體效率,本文提出一種結合UTD 算法和WW算法的混合全局減方差方法,其利用UTD 的偏倚因子動態調整WW 下限,利用WW 減小UTD 方法引起的權重波動,以此實現兩種算法的有機結合.這一方法在MC 粒子輸運程序cosRMC[12–14]上進行了驗證.第2 節介紹了UFS 和UTD 算法的基本思想;第3 節對混合算法的思想和實現方法進行了描述;第4 節基于新的指標深入研究了UTD算法的效率,并開展混合算法的測試驗證;第5 節給出了相應結論.

2 UFS 和UTD 算法原理

在反應堆模擬計算中,不同幾何柵元間的功率密度會有較大差異,全堆中子樣本數量就會呈現不均勻分布,導致全局計數不能同步收斂.UFS 算法的基本思想: 在保證結果無偏的前提下,對裂變中子源分布進行調整.由于MC 方法進行臨界計算是以迭代形式開展的,上一代產生的次級裂變中子將作為下一代的裂變中子源.基于這一特點,UFS算法根據當前代的裂變中子數密度分布產生偏倚因子,在下一代開始時指導裂變源分布的調整.為便于描述裂變中子源分布,在堆芯區域疊加均勻網格對空間進行離散,以網格為單元執行源粒子的偏倚.UFS 偏倚因子的設置方法為

其中,Nt為總裂變源中子數,m為總網格數,Ni為網格i內的裂變源中子數.

引入源偏倚因子βi后,網格i內每次碰撞產生的裂變中子數[15]將被調整為

其中,w是發生碰撞的中子權重;υ為平均次級裂變中子數;為宏觀裂變中子截面;是宏觀總截面.為保證計算結果無偏,下一代裂變源中子的權重ws將調整為ws/βi.

上述算法將導致低功率區域分裂出更多的小權重中子,而高功率區域則相應減少了裂變中子數,因此不會增加額外的計算耗時.如果減方差目標是展平某種全局計數的統計誤差分布,以目標計數密度指導源粒子的偏倚可能比基于裂變中子數密度的偏倚效率更高[9].基于此,UTD 算法提出偏倚因子的設定方法為

其中Tt為所有網格目標計數值之和;m為總網格數;Ti為網格i的目標計數值.上述兩種算法本質上都是源偏倚算法.

3 基于UTD 和WW 的混合全局減方差算法

WW 算法是一種基于分裂和輪盤賭的全局減方差方法,也需要借助網格來為不同空間區域提供WW.每一個網格的WW 由三個參數組成,包括WW 上限、WW 下限和輪盤賭存活權重.每當粒子到達柵元邊界、碰撞點以及飛行每個平均自由程后,都會對粒子的權重進行檢查.如圖1 所示,如果粒子權重低于WW 下限,就會觸發輪盤賭機制,有效地截斷小權重的粒子;如果粒子權重高于WW 上限,對粒子執行分裂操作,增加粒子樣本數.通過為低功率區域設置較小的WW 參數,為高功率區域設置較大的WW 參數,可以實現計算資源的均勻分配.WW 算法是一種輸運過程偏倚算法.

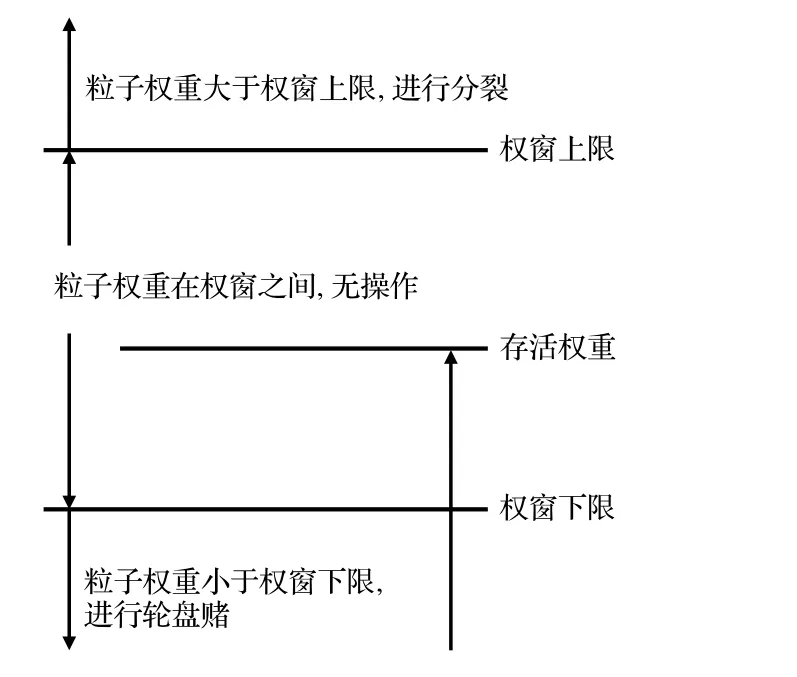
圖1 權窗原理Fig.1.Working principle of weight window.

為結合源偏倚與輸運過程偏倚各自的優勢,獲得臨界計算全局計數整體效率的進一步提高,本文提出一種基于UTD 和WW 的混合算法.由于UTD 算法會改變裂變中子的權重,可能會引起較大的粒子權重波動,不利于統計結果的整體收斂,而WW 算法可以將粒子權重控制在合理范圍內,因此混合算法預計可以獲得更高的整體效率.

UTD 方法和WW 方法均基于網格執行偏倚操作,因此在混合算法中兩者可以共用一套網格劃分方案.在低功率區域,UTD 和WW 方法都會分裂中子,混合算法將建立兩個臨時儲存庫,對這些粒子進行臨時分類存放,按序完成所有粒子的輸運模擬.由于UTD 算法在低功率區域會分裂出極小權重的中子,WW 的輪盤賭機制可能直接截斷這類粒子,對UTD 算法的效果造成一定削弱.因此,提出使用UTD 偏倚因子βi來調整網格WW 下限WL:

通過這種方法,在不同功率區域根據UTD 偏倚因子,合理地降低或抬高WW 下限,可以減少WW對UTD 性能的負面影響,實現兩種方法的有機結合.

4 數值結果及分析

選擇在Hoogenboom-Martin 壓水堆全堆基準題[16,17]上開展相關的測試驗證.如圖2 所示,該模型堆芯徑向半徑為209 cm,軸向高度為366 cm,共包含241 個燃料組件,燃料組件為 17×17 布置;每個組件內呈現17×17 的棒分布,包含264 個燃料棒和25 個控制棒通道.從圖2(a)和圖2(b)(不采用任何全局減方差算法)可以看出,基準模型的徑向功率分布具有顯著不均勻性,導致統計誤差分布也呈現嚴重不均.將堆芯沿橫向和縱向劃分成289×289 的網格,其中燃料區網格共計69649 個.計算條件為非活躍代數200,活躍代數300,每代初始粒子數50000,采用50 核并行計算,統計每個網格的中子裂變功率.

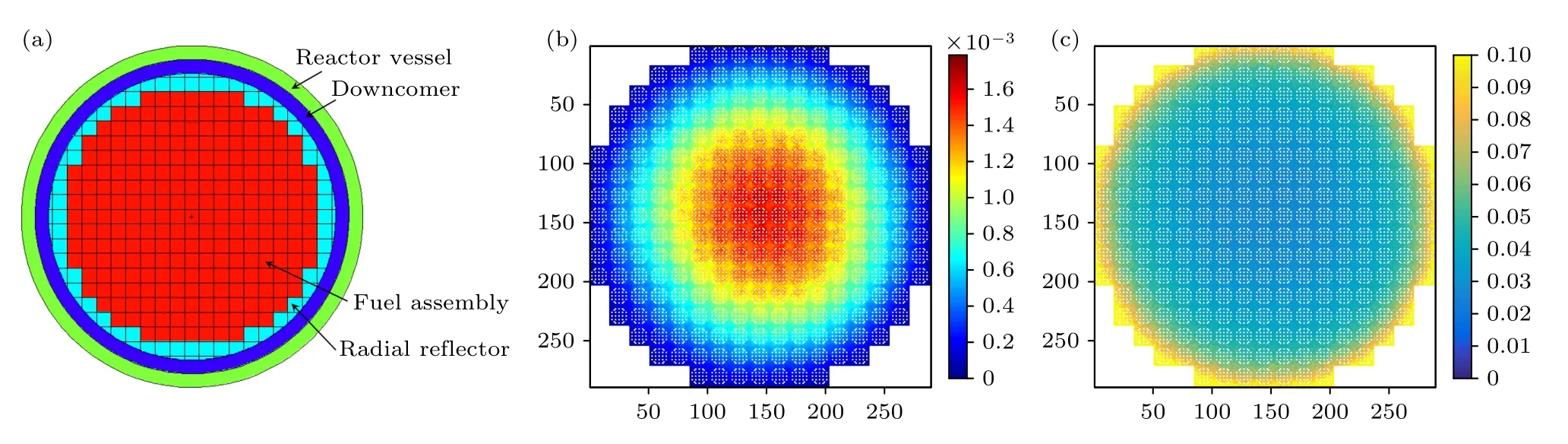
圖2 Hoogenboom-Martin 基準題(a) 幾何橫截面;(b) 功率分布(MW);(c) 統計誤差分布Fig.2.Hoogenboom Martin benchmark: (a) Geometric cross-section;(b) power distribution (MW);(c) statistical error distribution.

4.1 基于新指標的UTD 和UFS 對比分析

為更清晰地了解UTD 算法的優勢所在,基于新指標對UTD 和UFS 進行了對比分析.在H-M基準題計算中,堆芯模型具有1/4 對稱性,4 個對稱區域的物理量在理想情況下應完全相同,而由于統計誤差的存在,導致堆芯物理對稱區域的計算結果略有不同,稱之為計算不對稱性.引入變異系數Cυ定量描述這種計算不對稱程度,變異系數越大表示不對稱性程度越大[18]:

其中,S和分別是對稱區域4 個計數量的標準偏差和平均.

圖3 給出了Basic,UFS 和UTD 三種情況下的變異系數分布.從圖3 可以看出,不使用任何源偏倚的Basic 情況下,堆芯外圍的計算不對稱程度明顯比中心的不對稱程度大;使用UFS 算法時,堆芯外圍的Cυ明顯降低,計算不對稱程度較Basic的小;UTD 算法下的計算不對稱度相較UFS 有了更進一步的改善.

圖3 變異系數分布(a) Basic;(b) UFS;(c) UTDFig.3.Distribution of the coefficient of variation: (a) Basic;(b) UFS;(c) UTD.

此外,UFS 算法和UTD 算法在臨界計算的每個活躍代都會對偏倚因子進行更新,選取了堆芯中橫向289 個連續的網格,計算得到UTD 和UFS算法在這些網格中的偏倚因子的方差分布,見圖4.UTD 偏倚因子的方差整體小于UFS 偏倚因子的方差,UTD 算法的偏倚因子在迭代過程中波動更小,表明UTD 算法相比UFS 算法更具穩定性.

圖4 偏倚因子的方差分布Fig.4.Variance distribution of bias factors.

為了進一步對比兩者的減方差效果,引入品質因子FOM_MAX 和FOM_95 來表征計算效率[19,20]:

這里,T是計算時間,Remax是所有網格計數的統計誤差的最大值,Re95表示某一網格計數的統計誤差,其使至少95%的網格計數的統計誤差都不大于該值.表1 給出了三種計算條件下中子注量率的統計誤差和品質因子.從兩種品質因子來看,UTD 算法和UFS 算法均獲得了計算效率的提高,并且UTD 算法的計算效率略優于UFS 算法.在降低最大誤差的問題上,UTD 算法的計算效率是UFS 算法的1.36 倍.

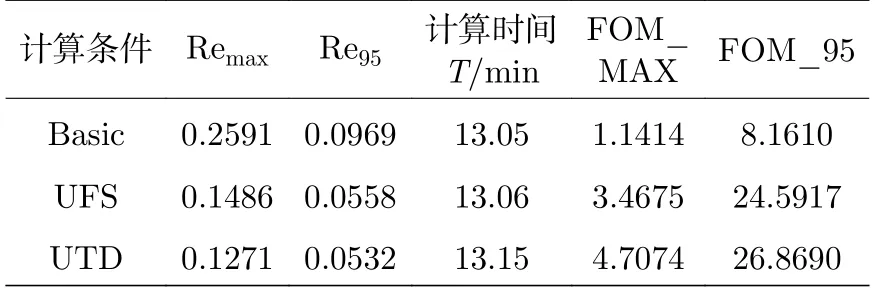
表1 UTD 算法和UFS 算法的計算結果對比Table 1.Comparison of calculation results of UTD and UFS.

4.2 混合算法的驗證

統計誤差的累積分布如圖5 所示,UTD 算法下的統計誤差較集中落在3.7%—5.0%區間內,混合算法和WW 算法下的統計誤差較集中落在2.7%—3.2%區間內.從結果可以看出,WW 算法下的統計誤差整體小于UTD 算法,且最大和最小誤差的差值相比UTD 算法也更小,說明WW 算法的減方差力度比UTD 算法更大.使用混合算法時,UTD 算法會在臨界計算中的每個活躍代開始對裂變源分布進行調整,WW 算法會在粒子輸運過程中對粒子進行偏倚,兩者的共同作用使得低功率區域具有更多的粒子樣本,在低功率區域實現更進一步的減方差效果,從而混合算法的最大統計誤差小于WW 算法和UTD 算法.表2 列出了三種減方差算法的整體效率,通過品質因子可以得出,針對降低最大誤差的問題,混合算法的計算效率分別是WW 算法和UTD 算法的2.6 倍和3 倍.

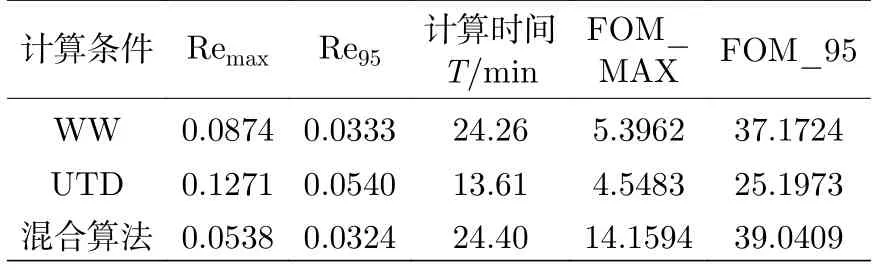
表2 計算結果對比Table 2.Comparison of calculation results.

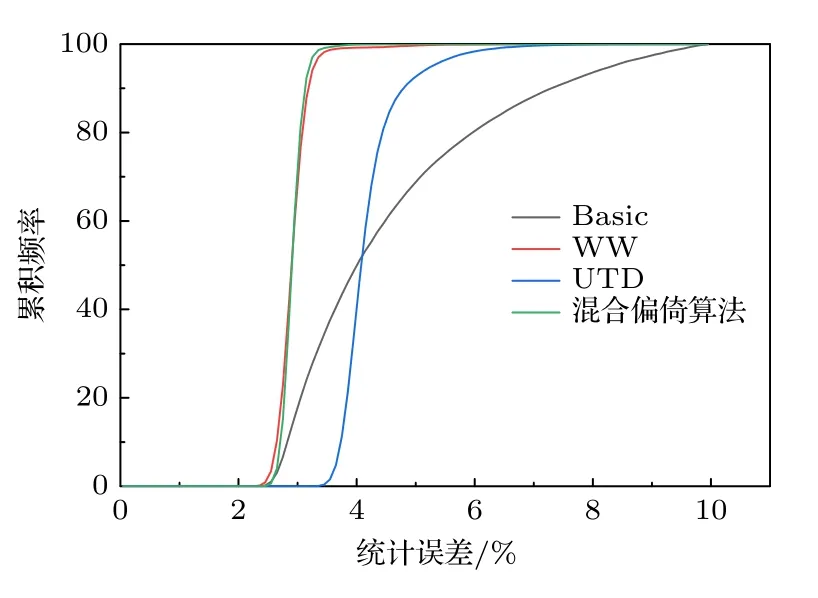
圖5 統計誤差的累積分布Fig.5.Cumulative distribution of statistical errors.

5 結論

圍繞MC 粒子輸運模擬全局計數問題統計誤差分布不均的問題,本文提出了一種結合均勻計數密度算法和WW 算法的混合算法,通過引入WW減少了均勻計數密度算法導致的權重波動,其WW 下限利用均勻計數密度算法偏倚因子進行調整,本質上實現了源偏倚和輸運過程偏倚的有機結合.在Hoogenboom-Martin 基準題的驗證計算中,基于新的指標對比分析了均勻計數密度算法和UFS 算法,進一步驗證了UTD 算法的高效性.同時,計算結果表明,混合算法的整體效率較均勻計數密度算法或WW 算法有進一步的提高.在降低最大誤差方面,混合算法的整體效率分別是WW算法和均勻計數密度算法的2.6 倍和3倍,驗證了混合算法的優越性.