基于2階Hann自卷積窗的諧波電能高精度量測方法研究與實現(xiàn)

李冬,艾黃澤,尹領,曾非同,周峰

(1.華中科技大學 電氣與電子工程學院,武漢 430074; 2.中國電力科學研究院有限公司,武漢 430074)

0 引 言

由于全球氣候變暖和能源危機等問題的出現(xiàn),能源行業(yè)不斷朝著可再生能源的方向轉(zhuǎn)型,以光伏發(fā)電為主的新能源裝機總量逐年遞增[1]。為了扶持戶用式光伏和工商業(yè)光伏的發(fā)展,國家制定了相應的度電補貼標準,根據(jù)全發(fā)電量對其進行分布式光伏發(fā)電補貼[2-3]。但補貼政策沒有考慮分布式光伏的供電質(zhì)量,從而無法約束分布式光伏并網(wǎng)對配電網(wǎng)造成的高頻次諧波污染[4-6]和電壓波動[7-9]等電能質(zhì)量問題。因此,研究分布式光伏的并網(wǎng)電能質(zhì)量,可為分布式光伏電價制定提供一個參考依據(jù),從而引導分布式光伏產(chǎn)業(yè)高質(zhì)量、可持續(xù)發(fā)展。

輸出電能諧波含量是分布式光伏電能質(zhì)量的關鍵指標之一。目前電網(wǎng)主要使用時分割乘法器電子式電能表,受前端傳感方式和計量算法等限制,其諧波電能計量誤差在百分級[10],不適合作為電能交易策略研究的電能質(zhì)量數(shù)據(jù)來源。為此,需要對分布式光伏設備中電能諧波進行單獨的高精度計量與數(shù)據(jù)收集。

諧波分析常采用快速傅里葉變換(FFT)[11],但該算法應用時會存在頻譜泄漏和柵欄效應的問題,進而影響諧波電能計量結(jié)果。對此,國內(nèi)外學者提出了多種改進方案,包括加窗插值FFT、準同步DFT、基于小波變換的時頻聯(lián)合分析算法[12]、Romberg積分算法[13]等。其中,加窗插值FFT是最常用的諧波分析算法,該算法采用主瓣寬度適宜、旁瓣衰減顯著的窗函數(shù)來抑制頻譜泄漏,并根據(jù)所選窗函數(shù)設計頻譜插值校正算法以減小柵欄效應造成的誤差[14]。經(jīng)典窗函數(shù)有Hann窗、Blackman窗、Nuttall窗和Kaiser-Bessel窗等[15],在此基礎上有學者提出自卷積窗[16-17]、旁瓣最低與最快速下降窗[18]等改進算法,并將其應用于電力諧波分析[19-20],獲得了優(yōu)越的檢測精度。在插值校正方面,有單峰插值和多峰插值等算法,其中雙峰譜線插值校正算法[21]是電能計量領域應用最普遍的插值算法之一。

針對分布式光伏諧波電能量測裝置,采用精度較高且易于實現(xiàn)的Hann自卷積窗與雙譜線插值算法是一種合適的選擇。然而,諧波電能表常采用DSP或MCU進行信號處理與分析[22-23],單核處理器對多通道多次諧波進行加窗插值FFT計算的實時性較差。

針對上述問題,本文提出了一種低運算資源消耗的順序型諧波計算流程,并在此基礎上優(yōu)化設計了一種多級流水線型諧波計算架構(gòu),大幅提升了加窗插值FFT的計算效率,基于ZYNQ系統(tǒng)實現(xiàn)了2階Hann自卷積窗及其雙譜線插值校正算法。此外,考慮ADC量化誤差,等效種因素的條件下開展了算法仿真實驗,提供了ADC位數(shù)、采樣點數(shù)N與窗函數(shù)的選擇依據(jù)。最后設計并開發(fā)了基于ZYNQ與LTC2358的諧波量測裝置板卡樣機,并給出了量測樣機的實測結(jié)果。

1 諧波算法仿真分析

1.1 2階Hann自卷積窗及其離散化

電能諧波計量系統(tǒng)中,為抑制頻譜泄漏對諧波參數(shù)計算帶來的影響,窗函數(shù)應具有旁瓣衰減效果好、復雜度低的特點。選擇2階Hann自卷積窗對ADC采樣數(shù)據(jù)進行時域截斷,其頻譜主瓣寬度合適、對旁瓣衰減效果優(yōu)異且算法實現(xiàn)難度適當[16]。窗長為T的Hann窗的時域表達式為:

(1)

定義Hann自卷積窗為若干個Hann窗進行自卷積運算[16],即:

(2)

式中p表示參與卷積的Hann窗個數(shù)。通過對p個Hann窗進行p-1次卷積運算,可以得到p階Hann自卷積窗,當p=1時,即為Hann窗本身。

以采樣率fs對式(1)進行時域離散化并右移T/2后,得到長度為M=Tfs的Hann窗序列:

(3)

式中n為離散采樣點的序號;M取2的整數(shù)次冪,以便于在嵌入式系統(tǒng)中實現(xiàn)該算法。根據(jù)傅里葉變換,序列(3)的頻譜函數(shù)為:

ω1∈[0,2π)

(4)

序列(3)的頻譜模函數(shù)為:

(5)

以頻率分辨率Δω1=2π/N對式(5)進行頻域離散化,得到長度為N=M的Hann窗離散頻譜模序列為:

(6)

對序列(3)進行p-1次離散自卷積操作,得到長度為pM-p+1的序列,然后在卷積序列的首尾添零,得到長度為N=pM的p階Hann自卷積窗序列。根據(jù)卷積定理,在時域上進行卷積操作等價于在頻域上進行乘積操作。因此,可以由序列(6)得到p階Hann自卷積窗的離散頻譜模序列,表示為:

(7)

1.2 Hann自卷積雙譜線插值算法

信號x(t)包含基波分量f0和直流分量、諧波分量,以采樣頻率fs對該信號進行采樣,得到長度為N的離散時域序列為:

(8)

式中h表示諧波次數(shù);Ah表示h次諧波的幅值;φh表示h次諧波的初相位。

采用2階Hann自卷積窗對序列x(n)進行加窗處理后,其離散頻譜為:

(9)

式中kh=hf0N/fs,表示第h次諧波頻譜峰值點對應的譜線號。存在頻率偏移時kh往往為非整數(shù),在柵欄效應的影響下,只能利用kh附近的其他譜線進行離散頻譜校正,才可確定kh的實際值,從而得到實際的頻率hf0。

忽略其他諧波對第i次諧波的頻譜干涉,此時,式(9)簡化為:

(10)

在第i次諧波峰值點附近的局部最大值和次大值之中,記靠左的譜線號為k1,靠右的譜線號為k2,顯然有k2=k1+1。記譜線校正量Δk=k1-ki,則Δk∈[-1,0]。引入?yún)?shù)α=Δk+0.5,顯然有α∈[-0.5,0.5],且k1-ki=α-0.5,k2-ki=α+0.5。

記k1、k2兩條譜線的模值分別為y1和y2,則有:

(11)

記校正系數(shù)v為:

(12)

結(jié)合式(10)～ 式(12)可以推導出:

(13)

通過式(12)可以利用y1和y2計算出校正系數(shù)v,再通過v求得α,但由于式(13)難以化簡為α關于自變量v的恒等式,故可以利用MATLAB的polyfit函數(shù),結(jié)合式(13)和式(7)對α關于v的反函數(shù)進行多項式擬合。擬合函數(shù)的階數(shù)選擇主要考慮因素是擬合精度,5階多項式擬合函數(shù)的均方根誤差RMSE=1.07×10-9,擬合程度優(yōu)異,更高的階數(shù)能夠帶來的擬合度提升有限,且會增大算法的工程量與處理器資源消耗,故本文采用5階擬合函數(shù):

α=-0.049178v5-0.062145v3-3.076222v

(14)

通過α求得譜線校正量Δk、校正后的頻率f、相位φ、幅值A分別為:

(15)

1.3 考慮ADC量化誤差的諧波分析仿真

實際工程中,使用ADC量化無法避免地會帶來量化誤差[24],在考慮ADC采樣條件下對算法精度進行仿真,為后續(xù)設計提供了ADC位數(shù)、采樣點數(shù)N與窗函數(shù)的選擇依據(jù)。

采用MATLAB對2階Hann自卷積窗及其雙譜線插值校正算法的諧波分析效果進行仿真,其流程也可用于指導FPGA程序設計,具體計算流程如圖1所示。

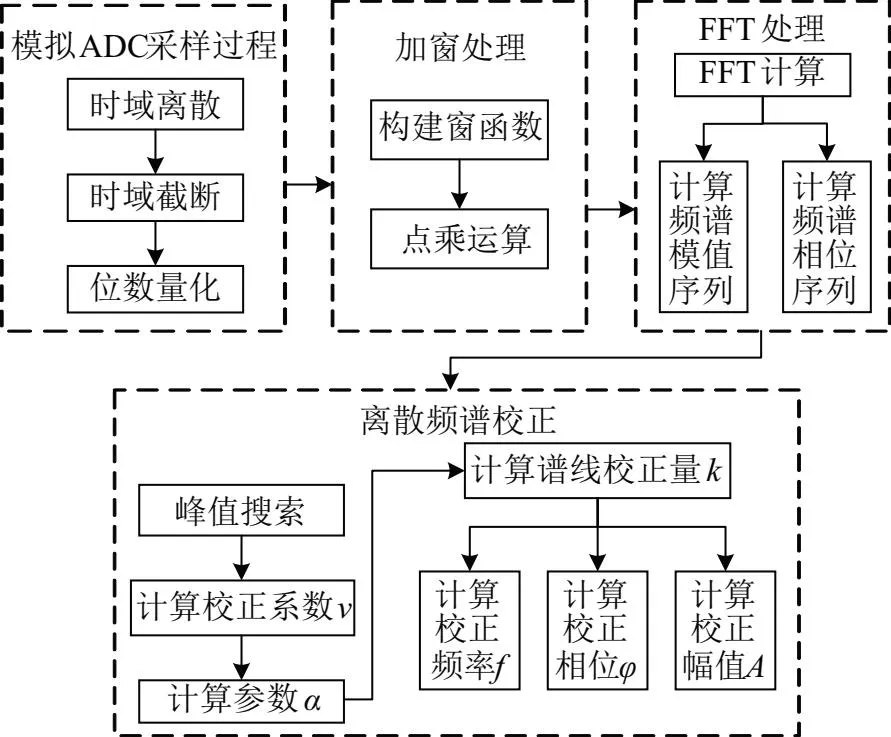
圖1 MATLAB仿真程序流程圖

1)模擬ADC采樣過程:以采樣率fs對時域連續(xù)信號x(t)進行采樣離散化,截取出長度為N的離散時域序列x(n),并采用式(16)對x(n)的元素逐個處理,模擬ADC位數(shù)量化過程,得到采樣序列用于諧波參數(shù)分析。

X(n)=[x(n)/K/(VIN+-VIN-)·LSB]

(16)

式中[·]代表四舍五入取整運算;K表示信號輸入ADC之前的變比,以電壓取樣及信號處理電路為例,其變比K= 1/66;(VIN+-VIN-)表示ADC輸入差分量程;LSB表示ADC的最低有效位,LSB= 2BADC,其中BADC表示ADC的位數(shù)。取整后的離散點序列需滿足|X(n)|∈[0,LSB]∩Z。

2)采樣序列加窗:調(diào)用MATLAB中的hann函數(shù)構(gòu)造長度為N/2的Hann窗序列,進行1次自卷積操作,并在末尾添加0擴展得到長度為N的自卷積窗序列,最后將其進行幅值歸一化,即得到所需的2階Hann自卷積窗序列。將長度為N的ADC采樣序列點乘長度相同的2階Hann自卷積窗序列得到加窗后的采樣數(shù)據(jù),作為FFT模塊的實部輸入。

3)FFT:調(diào)用fft函數(shù)對加窗序列進行N點FFT處理,得到復數(shù)序列。然后采用abs函數(shù)處理該復數(shù)序列并乘以系數(shù)2/N得到頻譜模值序列,采用angle函數(shù)處理該復數(shù)序列得到頻譜相位序列。

4)離散頻譜校正:確定離散頻譜峰值參數(shù),根據(jù)模值序列、頻率f、采樣率fs、采樣點數(shù)N,采用Nf/fs計算頻率f處對應譜線號的理論值,在該譜線的左右5條譜線范圍內(nèi)搜索,遍歷找到局部最大值和次大值對應的譜線號。然后根據(jù)式(12)計算校正系數(shù)v,利用式(14)對α關于v的反函數(shù)進行多項式擬合從而計算出α,進而得到譜線校正量Δk。最后將Δk代入式(15)得到頻率f、相位φ、幅值A的校正結(jié)果。

1.3.1 不同ADC采樣位數(shù)時的檢測誤差

ADC量化給基于2階Hann自卷積窗的諧波分析算法帶來一定誤差,本節(jié)改變式(16)中的LSB,對ADC量化誤差造成的影響進行仿真分析,采用下述序列探究不同ADC位數(shù)對諧波檢測誤差的影響。

(17)

式中信號1:f1= 50 Hz、A1= 311 V、φ1= 0;信號2(弱幅值):f2= 150 Hz、φ2= π/6、A2在0.4～3.1 V之間變化,步進為0.1 V;采樣率fs= 25 000 Hz,N= 8192。令ADC位數(shù)BADC分別為16、24以及MATLAB默認精度(即不考慮ADC量化)進行誤差分析,其結(jié)果如圖2所示。

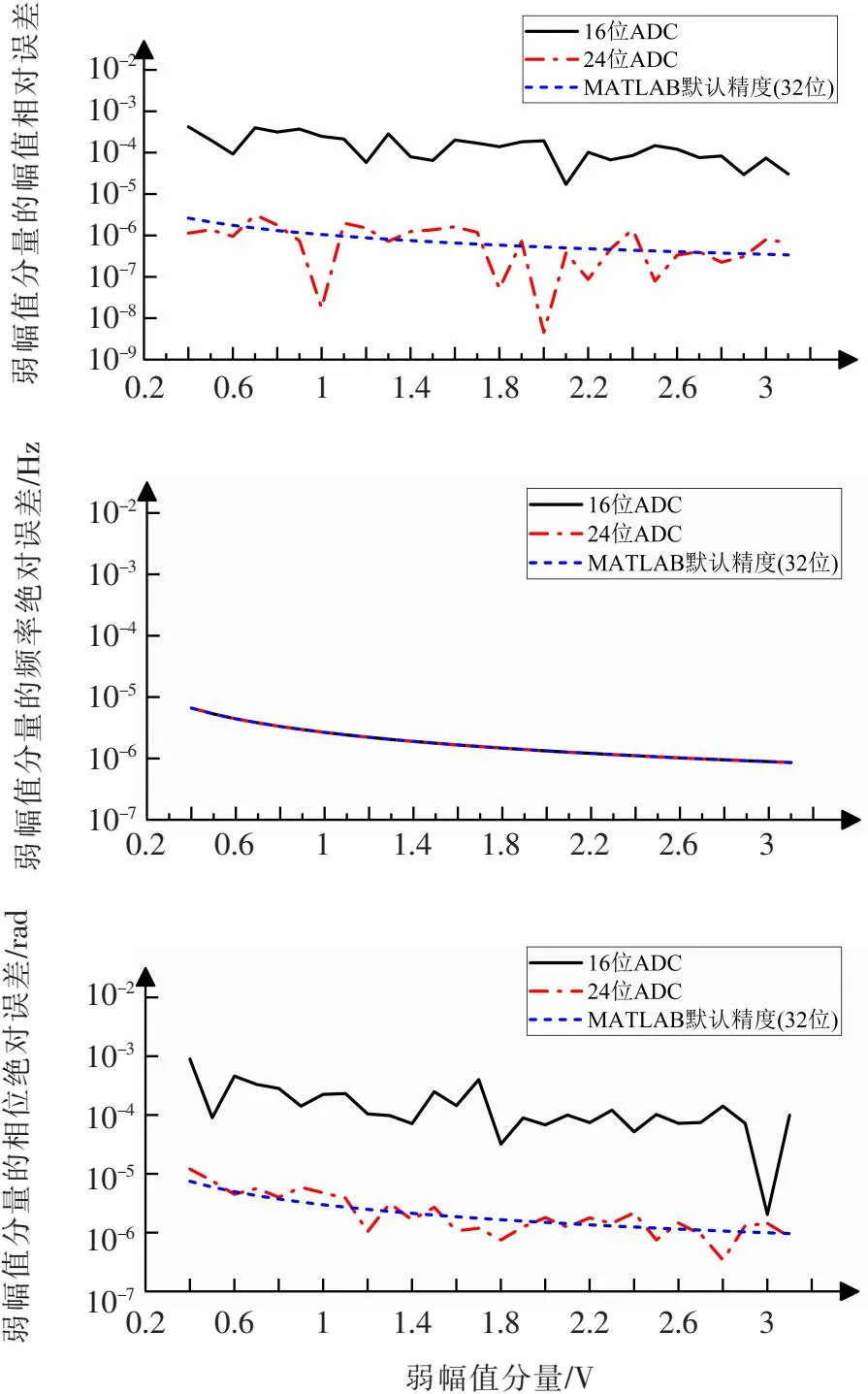
圖2 不同ADC采樣位數(shù)時弱信號參數(shù)分析誤差

ADC采樣位數(shù)的選擇關系到測量系統(tǒng)的硬件實現(xiàn)成本與資源消耗。由圖2可見,在MATLAB默認仿真精度(不考慮ADC量化),各參數(shù)誤差曲線平滑。考慮ADC量化時,ADC位數(shù)對弱諧波信號的頻率檢測誤差幾乎無影響。但是,對于幅值和相位檢測誤差,采用更高的ADC采樣位數(shù)能獲得更高的分析精度,達到一定的ADC采樣位數(shù)后,其誤差精度在MATLAB默認仿真精度附近波動。說明更高的ADC采樣位數(shù)能夠更好地發(fā)揮算法的精度優(yōu)越性,當ADC位數(shù)較低時,量化誤差會導致算法的精度被ADC位數(shù)所鉗制。

當BADC=16時,諧波分量的幅值相對誤差在0.1%以內(nèi),相位絕對誤差在0.000 5 rad以內(nèi),仍具有較高的準確度,滿足本文的諧波測量系統(tǒng)精度需求。

1.3.2 不同采樣點數(shù)N時的檢測誤差

針對采樣點數(shù)N對基于2階Hann自卷積窗的諧波檢測誤差的影響進行仿真分析,作為后續(xù)算法實現(xiàn)選擇采樣點數(shù)的依據(jù)。采用式(16)對式(17)進行量化處理。式中,信號1(基波):f1= 50 Hz、A1= 311 V、φ1=0;信號2(3次諧波):A1=10 V、f2=150 Hz、φ2=π/6。

ADC的位數(shù)選擇BADC=16,取采樣點數(shù)N從2 048～65 536,步進為512。對2階Hann卷積窗對其進行諧波分析,所得各信號分量的頻率、幅值和初相位分析誤差隨采樣點數(shù)N變化的曲線如圖3所示。

圖3 采樣點數(shù)N不同時諧波參數(shù)分析誤差

采樣點數(shù)N的選擇關系到處理器的FFT計算時間與計算資源消耗大小。由圖3可見在采樣點數(shù)N=8 192之前,隨著N增大,各信號分量的三參數(shù)誤差呈減小趨勢;N繼續(xù)增大時,受譜線校正量Δk的波動,誤差呈周期性變化趨勢。

當N=8 192時幅值相對誤差在0.02%以內(nèi),初相位絕對誤差在0.000 5 rad以內(nèi)。綜合考慮算法的準確度和實時性需求,采用N=8 192較為合理。

1.3.3 不同窗函數(shù)的弱幅值信號檢測誤差

弱幅值諧波分量的檢測精度關系到諧波電能計量的精度。當弱幅值諧波分量附近存在其它基波或諧波分量時,隨著弱諧波分量相對幅值降低,其受到頻譜泄漏的影響增大,參數(shù)分析的準確度會降低。Hann自卷積窗具有較好的旁瓣性能,可以很好地抑制頻譜泄漏對弱幅值諧波分析的影響。本節(jié)將驗證不同窗函數(shù)對弱諧波分量的參數(shù)分析效果。

采用式(16)對序列式(17)作ADC量化處理。式中,信號1:f1=50 Hz、A1=311V、φ1=0;信號2(弱幅值):f2= 150 Hz、φ2=π/6、A2在0.4～3.1 V之間變化,步進為0.1 V。取ADC的位數(shù)為BADC= 16,N=8 192。基于的Hann窗、2階Hann卷積窗、4項3階Nutuall窗對信號序列進行諧波分析,所得弱幅值諧波頻率、幅值和初相位的誤差隨信號中該諧波幅值變化的曲線如圖4所示。

圖4 不同窗函數(shù)下弱幅值信號參數(shù)分析誤差

觀察圖4可知,在模擬ADC采樣情況下,2階Hann自卷積窗、4項3階Nutuall窗的弱幅值分量的幅值、相位誤差相比于Hann窗降低了2個數(shù)量級;頻率誤差相較Hann窗降低了4個數(shù)量級。其中,2階Hann自卷積窗、4項3階Nutuall窗誤差曲線重合的原因是ADC位數(shù)鉗制了算法發(fā)揮更高的分析精度。

2 諧波量測裝置硬件設計

諧波量測裝置板卡樣機的硬件框圖如圖5所示,主要由電流傳感器及信號處理電路、電壓取樣及信號處理電路、模數(shù)轉(zhuǎn)換器(ADC)、ZYNQ控制器與三相載波模塊構(gòu)成。諧波量測裝置從光伏系統(tǒng)的三相節(jié)點上對電壓電流進行取樣與處理,通過ADC采樣并通過ZYNQ進行諧波分析與計算,將得到的電能結(jié)果通過載波模塊發(fā)送給電能采集終端。

圖5 諧波量測裝置硬件框圖

諧波量測裝置的硬件設計核心在于數(shù)據(jù)采集單元和數(shù)據(jù)處理單元。首先,考慮諧波測量的精度問題,且系統(tǒng)需具備采集從直流到高次諧波信號的能力,數(shù)據(jù)采集單元的ADC與傳感器選型十分重要;其次,由于系統(tǒng)的多通道多次諧波的快速計算與數(shù)據(jù)實時上傳需求,主控制器的選型也較為關鍵。本文將重點介紹這兩個方面的硬件設計與選型思路。

2.1 數(shù)據(jù)采集單元

由于量測裝置需具有50次以內(nèi)的諧波分析能力,根據(jù)奈奎斯特定理可知ADC采樣率應在5 ksps以上,為了留有足夠的裕度,故選擇最高采樣率在25 ksps以上的ADC;考慮ADC的量化誤差,根據(jù)裝置的準確度等級要求,應選擇13位及以上的ADC。綜合考慮準確度和硬件實現(xiàn)成本,選用LTC2358-16,它是一款16位8通道同步采樣ADC,每通道最高采樣率200 ksps。

電流傳感器選型主要考慮可測信號的幅值范圍、頻率范圍、測量精度、1 min絕緣耐壓等級等參數(shù)。CSA101-G050T01電流傳感器可將幅值±100 A的一次電流轉(zhuǎn)換為±50 mA的二次電流,信號頻率范圍0～100 kHz,測量精度0.02%,1min絕緣耐壓5 kV,符合取樣器選型要求。電壓取樣裝置由電阻分壓器與抗混疊濾波器組成,其中分壓器的低壓端電阻與并聯(lián)電容共同組成抗混疊濾波器對信號進行濾波。

2.2 數(shù)據(jù)處理單元

數(shù)據(jù)處理單元選型需考慮諧波電能的實時性計算,FPGA作為可編程邏輯器件,具有高速、并行運行及設計靈活等優(yōu)勢,相較于MCU與DSP更適用于多通道多次諧波的大計算量使用場景。本文選用Zynq7000系列芯片作為主控制器,型號為XC7Z035-2FFG676,該芯片集成了FPGA可編程邏輯和ARM處理器,基于AXI總線協(xié)議實現(xiàn)ARM與FPGA之間的高效片內(nèi)互聯(lián)。FPGA用于實現(xiàn)ADC數(shù)據(jù)采集、數(shù)據(jù)緩存、卷積窗FFT與離散頻譜校正等功能;ARM用于實現(xiàn)原始電能數(shù)據(jù)的解析計算、載波通信等功能。

3 諧波分析程序架構(gòu)設計與實現(xiàn)

基于ZYNQ的諧波分析程序整體設計框圖如圖6所示,主要分為數(shù)據(jù)采樣緩存模塊、諧波分析模塊與BRAM數(shù)據(jù)交互模塊。

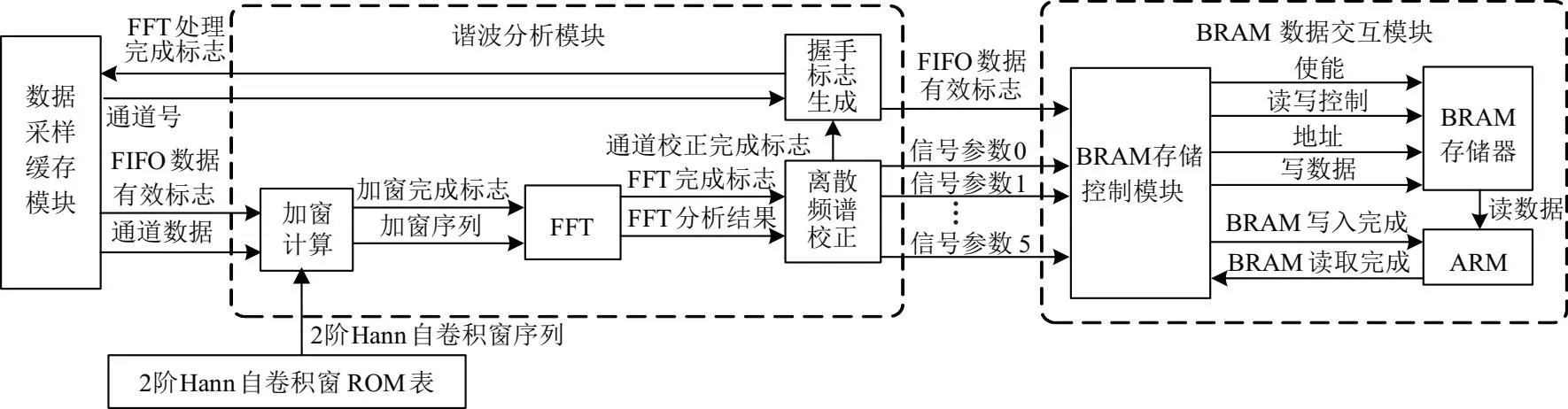
圖6 諧波分析程序整體框圖

數(shù)據(jù)采集緩存模塊將6個通道的ADC采數(shù)據(jù)存入FIFO中,在接收到FFT處理完成標志位時,開始將FIFO數(shù)據(jù)依次寫入FFT數(shù)據(jù)處理模塊進行加窗、FFT與離散頻譜校正。所得到的6個通道校正后的幅值頻率相位數(shù)據(jù)通過BRAM存儲控制模塊與內(nèi)置ARM進行數(shù)據(jù)交互,然后在ARM內(nèi)完成數(shù)據(jù)的解析與載波發(fā)送。

由于系統(tǒng)需進行多電壓電流通道的多次諧波參數(shù)計算,在保證參數(shù)測量精度的同時要做到高時效性。所以,諧波分析模塊的數(shù)據(jù)鏈路設計與程序架構(gòu)設計合理性尤為重要。本節(jié)著重介紹諧波計算的數(shù)據(jù)鏈路設計與諧波計算架構(gòu)。

3.1 諧波分析模塊數(shù)據(jù)鏈路設計

諧波分析模塊的數(shù)據(jù)鏈路如圖7所示。為了降低FPGA計算帶來的量化誤差與截斷誤差,在計算資源合理需求的范圍內(nèi)對各個寄存器變量選取合適的位數(shù)。

圖7 諧波分析模塊數(shù)據(jù)鏈路圖

首先由FIFO緩存的ADC數(shù)據(jù)通過乘法器與Hann自卷積ROM表進行點乘;乘法器輸出數(shù)據(jù)流給FFT IP核,經(jīng)過FFT計算輸出的實部與虛部結(jié)果分別通過自乘法器、加法器與平方根器,得到原始FFT輸出數(shù)據(jù)的幅值序列譜。

基于幅值序列譜,在n次諧波理論頻率附近±5根譜線的范圍依次進行峰值和次大值譜線搜索,得到各頻率的譜線號k1、k2和對應的模值y1、y2;根據(jù)式(12),利用y1、y2計算校正系數(shù)v;接下來采用式(14)的多項式擬合α關于v的反函數(shù),進而根據(jù)α=Δk+0.5得到譜線校正量Δk;根據(jù)式(15),分別構(gòu)造幅值、頻率、相位校正模塊,將譜線校正量Δk、譜線序號k1、k2、幅值序列、實部虛部序列輸入對應的校正模塊中,求得n次諧波的各項校正參數(shù)。

3.2 諧波分析模塊程序架構(gòu)設計

3.2.1 順序型諧波計算流程

多通道ADC數(shù)據(jù)實現(xiàn)加窗、FFT與離散頻譜校正功能若實例化多個同一功能的模塊進行計算將耗費大量LUT資源。為此,設計一種順序型諧波計算流程,如圖8所示。多通道ADC數(shù)據(jù)分通道進行諧波處理,順序型諧波計算同一時間只能處理ADCm通道的第n次諧波,處理完畢后再進行下一次諧波的處理,直到6路ADC通道的50次諧波均處理完畢,才開始下一時刻點的ADC采樣序列諧波計算。

圖8 順序型諧波計算流程

3.2.2 多級流水線型諧波計算架構(gòu)

低資源消耗的順序型諧波計算需要逐次諧波、逐模塊進行計算,將耗費大量時間。為發(fā)揮FPGA并行計算的優(yōu)勢,在順序型計算流程基礎上優(yōu)化設計了一種多級流水線諧波計算架構(gòu),可顯著提升多次諧波的計算效率。如圖9所示,多級流水線諧波計算架構(gòu)由各個子模塊流水線組成。當ADCm通道的諧波計算開始時,頻率輸出流水線首先將基波搜索頻率F1輸出給譜線搜索流水線,譜線搜索流水線在計算出基波譜線號k1、k2后輸出給校正系數(shù)v流水線,并將譜線搜索完畢標志置1,獲取下一次諧波的搜索頻率F2并等待v計算完畢標志拉高再開始下一次諧波譜線號的輸出。

若校正系數(shù)v流水線已將v計算完畢標志拉高,而譜線搜索流水線未完成下一次諧波的計算,那么校正系數(shù)v流水線將等待譜線搜索流水線的輸出有效信號拉高時再開啟下一次計算。其余流水線的計算模式均同上。

3.2.3 子模塊狀態(tài)機設計

諧波計算架構(gòu)的各個子模塊均采用狀態(tài)機的邏輯結(jié)構(gòu)實現(xiàn),以校正系數(shù)v計算模塊為例說明本文狀態(tài)機的設計方法,如圖10所示。在校正系數(shù)計算環(huán)節(jié),首先進入radio_Init狀態(tài),此狀態(tài)下將各變量置0,并基于最大譜線搜索模塊計算得到的k1、k2;接下來進入radio_On狀態(tài),此狀態(tài)下延遲計數(shù)變量cnt會在每個時鐘上升沿自加1,當cnt∈[2,6]時,讀取幅值序列RAM中k1、k2所對應的模值y1、y2,并且根據(jù)式(12)計算被除數(shù)與除數(shù);當cnt∈[7,8]時,將被除數(shù)與除數(shù)輸入給除法器IP核進行計算;最后進入radio_Finish狀態(tài),等待除法器的valid標志位置1,保存除法器的輸出結(jié)果存入寄存器變量,等待下一次計算流程開始。

圖10 校正系數(shù)v計算狀態(tài)機流程圖

4 實驗與測試

基于0.05級電子式互感器檢測平臺和PA8000系列功率分析儀對量測裝置板卡樣機的計量準確度進行測試,測試環(huán)境如圖11所示。其中,0.05級電子式互感器檢測平臺作為功率源,輸出符合測試條件的電壓、電流給功率分析儀和量測裝置;PA8000功率分析儀作為標準測量儀表,基本精度為0.01%,測量帶寬為直流和0.1 Hz～5 MHz交流,將其測量結(jié)果作為標準值與量測裝置樣機的實測值比較,得到量測裝置樣機的誤差。

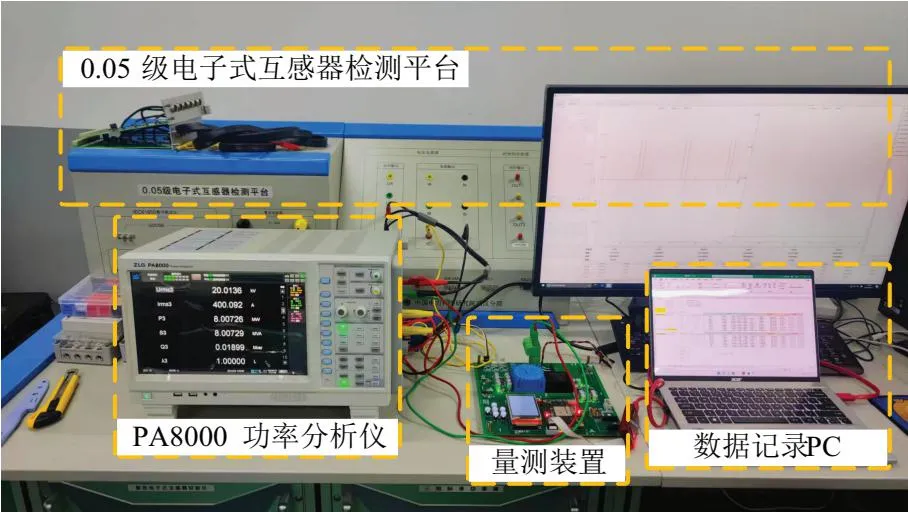
圖11 量測裝置測試平臺

4.1 基波測量誤差

根據(jù)C級靜止式有功電能表標準[25]、0.5 S級靜止式基波頻率無功電能表標準[26]及相應的交流電測量設備試驗標準[27],對量測裝置樣機進行電流改變與頻率偏移引起的功率誤差測試。

受限于0.05級電子式互感器檢測平臺輸出電壓上限為200 V,電流上限為40 A,下限為0.14 A的限制。將測試參數(shù)設置為:基波電壓為200 V、額定電流Ib= 40 A、轉(zhuǎn)折電流Itr= 1 A、最小電流Imin= 0.24A、啟動電流Ist= 0.14 A。

電流改變引起的誤差測試、頻率偏移引起的誤差測試結(jié)果分別如表1、表2所示。

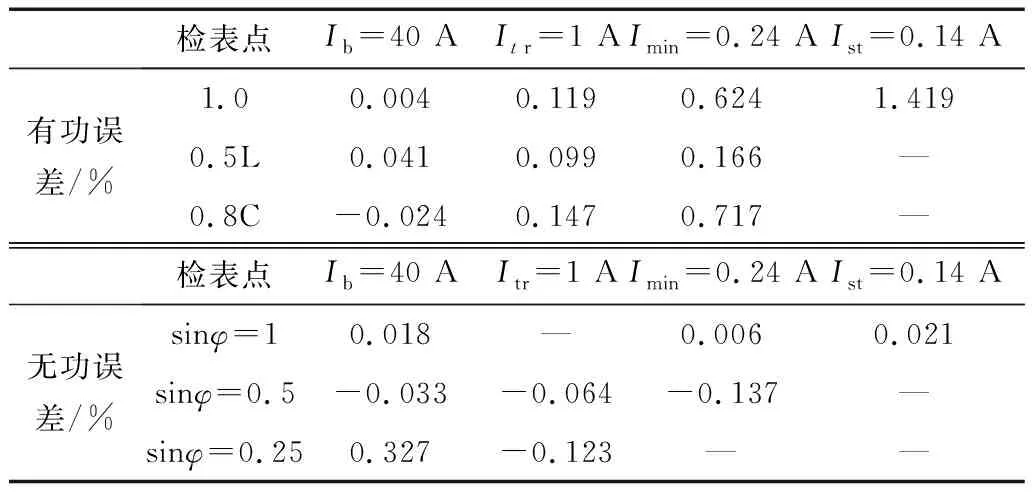
表1 不同電流情況下的功率測量誤差

表2 不同頻率下的功率測量誤差

測試結(jié)果表明,樣機的基波測量準確度滿足C級靜止式有功電能表標準與0.5 S級無功測量儀表檢定標準的要求。觀察測試結(jié)果可知,在兩種測試條件下,均存在電流低于Imin時誤差顯著增加的現(xiàn)象,考慮是較小電流的條件下ADC采樣幅值較小,實際電路引入的噪聲干擾與FPGA算法實現(xiàn)過程中的位數(shù)截斷問題顯著增加了參數(shù)測量誤差。

4.2 諧波測量誤差

根據(jù)公用電網(wǎng)諧波標準[28]和光伏系統(tǒng)并網(wǎng)技術要求[29],對量測裝置樣機進行諧波測量準確度測試,設置基波電壓200 V,基波電流40 A,包含3～21奇次諧波,各次諧波的電壓、電流含量如表3所示,其中h為諧波次數(shù),uh為諧波電壓相對基波電壓的比值,ih為諧波電流相對基波電流的比值。測試結(jié)果中,3～21次奇次諧波的電壓、電流幅值相對誤差和電壓、電流相位差如表4所示,結(jié)果表明,量測裝置樣機的諧波準確度滿足A級諧波測量儀表檢定標準的要求。

表3 測試信號的各次諧波含量

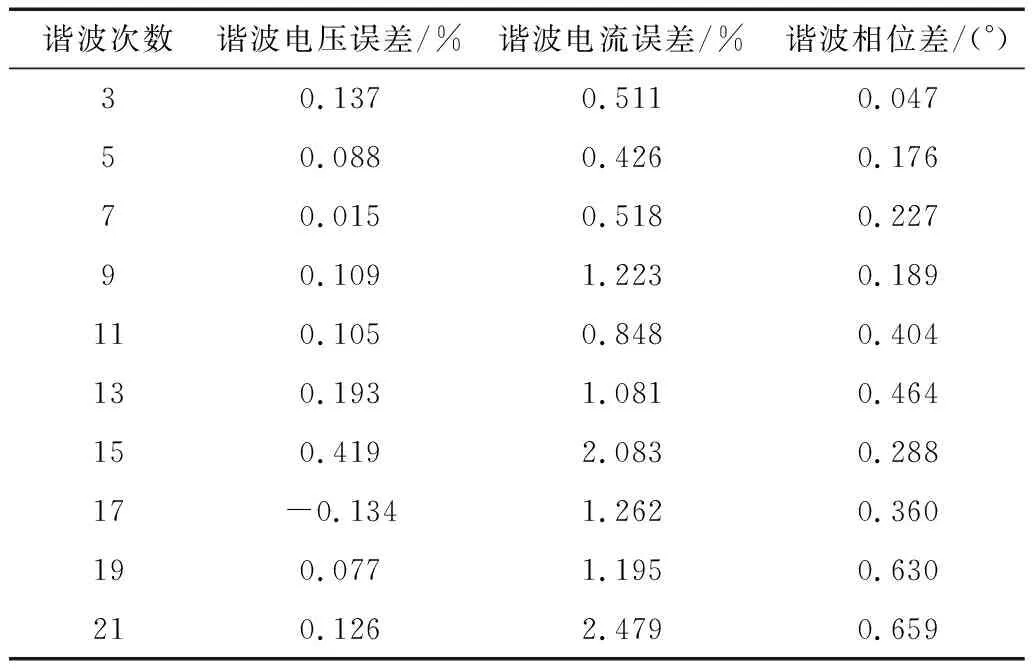
表4 諧波測量誤差結(jié)果

其中,15～21次諧波參數(shù)的相位角誤差增大,考慮是取樣電路無源濾波器在不同頻率下的相移所導致;幅值誤差增大是由于實際電路引入的噪聲干擾與FPGA算法實現(xiàn)過程中截斷誤差共同影響所致。可考慮采用更高位數(shù)的ADC,并對取樣信號輸入通道設計多擋位放大切換功能將弱諧波信號放大后采樣,進而提高諧波檢測精度。

5 結(jié)束語

本文提出了一種多級流水線型的諧波計算架構(gòu)大幅提升了加窗插值FFT的實時計算效率,基于ZYNQ系統(tǒng)實現(xiàn)了2階Hann自卷積窗及其雙譜線插值校正算法。考慮ADC量化誤差,對2階Hann自卷積窗及其雙譜線插值校正算法的諧波分析效果進行仿真,提供了ADC位數(shù)、采樣點數(shù)N與窗函數(shù)的選擇依據(jù)。基于ZYNQ與LTC2358,設計并開發(fā)了諧波量測裝置的板卡樣機。經(jīng)實驗測試,樣機的基波測量誤差滿足C級靜止式有功電能表標準與0.5S級無功測量儀表檢定標準的要求。此外,諧波測量誤差結(jié)果顯示該樣機的準確度滿足A級諧波測量儀表檢定標準的要求。