立足本手,方得妙手*
——對2022 年廣州市中考數學第24 題的探究

廣東省廣州市第五中學(510220) 劉護靈

2022 年全國新高考Ⅰ語文卷,以“本手、妙手、俗手”這三個圍棋術語為切入點,告訴我們要打好基本功,沉潛努力,我們才會有機會靈光一現,神來一“手”,才有可能一鳴驚人,做出成績.我們以2022 年廣州市中考數學第24 題為例,通過兩個解法的探討和改進,讓我們更加深刻的認識到“立足本手,守正創新”的深刻道理,在解析的過程中,我們利用了強大的GeoGebra 進行精準繪圖,實驗探究,使得講解更加生動.

1 呈現原題

24.己知直線l:y=kx+b經過點(0,7)和點(1,6).

(1)求直線l的解析式;

(2)若點P(m,n)在直線l上,以P為頂點的拋物線G過點(0,-3),且開口向下

①求m的取值范圍;

②設拋物線G與直線l的另一個交點為Q,當點Q向左平移1 個單長度后得到的點Q′也在G上時,求G在的圖象的最高點的坐標.

前2 問的簡析:(1)根據待定系數法求出解析式即可得到直線l解析式為:y=-x+7;

(2) ①由于點P在直線l上,那么可以得到m與n的關系,得n=-m+7,然后根據頂點式得到拋物線G的解析式:y=a(x-m)2-m+7,代入點(0,-3)的坐標得由于拋物線的開口向下,所以a＜0,所以m的取值范圍是m＜10且m≠0.本文重點探討(2) ②.

2 立足“本手”

2.1 “本手”——求拋物線和直線的交點

此題關鍵條件是“拋物線G與直線l的另一個交點為Q”,如何求交點Q? 本質上是聯立拋物線方程和直線l的方程,求這組方程的解.根據條件,因為點P(m,n)在直線l上,所以n=-m+7;由拋物線的頂點式,可得拋物線G方程為:y=a(x-m)2-m+7,由2 ①知,所以不少學生毫不猶豫的把a代入,得到-m+7,此時聯立直線方程:y=-x+7,消去y,得到-x+7=-m+7,此時這個含參方程,學生求解的難度比較大!

如果直接去分母,得(-x+7)m2=(m-10)(x-m)2+(7 -m)m2,接下來移項,化簡,再利用十字相乘法或者求根公式,求得兩個交點,x1=m(和點P重合,舍去),中間的運算量比較大,考場緊張的狀態下可能容易算錯!

如何簡化上述求交點的過程? 思路是保留a,相當于“先換元,再解方程”.即聯立y=a(x-m)2-m+7和y=-x+7,消去y,得a(x-m)2-m+7=7-x,化簡得a(x-m)2+x-m=0,解決這個方程就比較簡單了,直接可以看出因式分解:(x-m)[a(x-m)+1]=0,所以x1=m(和點P重合,舍去),x2=+m,此時再把a代入x2,容易得x2=,這樣就得到了點Q的橫坐標.

2.2 反思和啟示

聯立拋物線和直線方程,求交點坐標,當含參計算時,往往是“先換元,再解方程”,使得計算量比較小,其根本原因是,不論a還是m,都是參數.我們需要把x當成主元,通過換元,使得關于x的方程盡可能的簡單,這樣求解這個一元二次方程就比較簡便.

學生在考試中,運算量的減少,至少有兩個好處,好處一,讓我們的計算準確性得到了提高,好處二,讓學生在緊張的考試時間內,有時間繼續解答后面的題目.

解決這類問題的實質,是學生需要學習并理解含參的一元二次方程,如何求解比較簡潔、計算量少! 即提高解決含參的方程求解能力,是“本手”.

2.3 繼續求解

得到x2=+m=m-之后,也不需要把a代入x2,去得到x2=,而是保留x2=m-的形式,繼續進行運算,最后才把a代入.

當m值確定 之 后,問 題的≤x≤+1 這個范圍也是完全確定的,只是需要對于m的不同情況進行分類討論.當m=時,拋物線G為y=-2x2-10x-3,對稱軸為直線x=,對應區間為-2 ≤x≤-1,整個區間在對稱軸x=的右側,此時,函數值y隨著x的增大而減小,如圖1,當x取區間左端點x=-2 時,y達最大值9,最高點坐標為(-2,9);當m=2時,對應區間為最高點為頂點P(2,5),如圖2,G在指定區間圖象最高點的坐標為(-2,9)或(2,5).

圖1

圖2

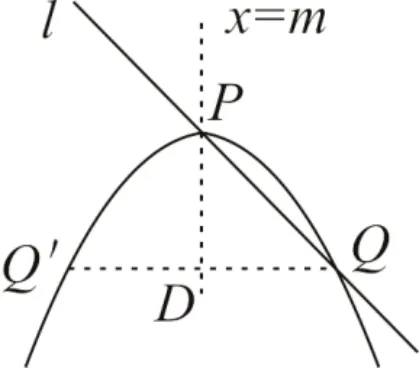
圖3

3 “妙手”生成

3.1 “妙手”——根據軸對稱,巧妙的設點坐標,再代入拋物線方程

聯立直線和拋物線求交點,是此題的“本手”,同時計算的過程也是難點.能否“繞過求交點這一步”,進一步的簡化計算呢? 可以!

這個解法在計算量上比“本手”解法小了很多,時間上也得到了節省.

3.2 反思和啟示

“妙手”的求解關鍵在于此類問題中,點Q和Q′是關于某條已知直線對稱的,所以先設點Q的坐標,則Q′的坐標即刻可求,最后再把點Q′的坐標代入拋物線的方程,這樣可以避免聯立求方程組的解而產生的運算量.

這樣的方法深刻的體現出了“方程——曲線”的完備性和純粹性,也深刻體現了充分利用圖形的特征,可以使計算過程得到優化和簡化.

在上面的分析中,也可以看出近年廣州市中考數學關于拋物線等問題的命題特點,“無圖想圖”,“無圖畫圖”,學生的畫圖能力、分析能力、計算推理能力都非常重要,也是進入高中學習的必備的關鍵能力.

4 教學啟示

4.1 借助GeoGebra 有效提高學生對“含參”問題的理解

此題是二次函數有關的問題,需要根據自變量的取值范圍進行求解.通過深入剖析此題,我們深刻的認識到,此題的“本手”是含參的一元二次方程的求解,它是基本知識、基本原理與基本技能.在初中數學教學中,“參數問題”由于其高度的抽象性和復雜性,“很難教”,是所有初中數學教師面臨的最棘手的問題之一.以往的傳統教學,很難讓學生直觀感受參數變化導致的圖像變化過程,而GeoGebra 則能有效解決這一痛點.筆者也借助了該軟件繪制本題的精準圖形.實際上,GeoGebra 擁有簡潔明了的界面、操作簡單、容易上手、各平臺通用等特點,利用GeoGebra,建立滑動條,可以有效的演示初中數學“含參問題”,并且在滑動條的拉動過程,讓學生深入其境的感受參數對于圖形的影響,可以進行更多深入的實驗探究.

4.2 實驗探究和邏輯推理雙翼齊飛

在教學中,使用GeoGebra 為學生創設探究情境,生動還原“參數”對于圖像的影響,但是,技術融合數學教學的基本原則是:始于直觀想象,終于邏輯推理.GeoGebra 或其它畫板可以為學生展示豐富多彩、廣博生動的教學內容,比如圖形的平移、旋轉、縮放、分割、重疊等,既生動又準確,再與學生動手操作相結合,其過程充滿趣味性和挑戰性! 但運用GeoGebra,需防止“錯位”、“越位”、“缺位”! GeoGebra 只是輔助教學手段,不能盲目擴大,造成錯位,這些是我們一線老師需要注意的問題.GeoGebra 在于促進學生有效思考,在于提升學生對數學本質的理解,不能越位而使學生缺失經歷知識的形成過程,而應突出體現其探究性,輔助課堂上給予學生充分參與數學活動的時間和機會.當然,GeoGebra 是學生自主學習探究的一種認知工具,這一理念體現不能缺位.不能只強調其作為輔助教學的演示工具,而忽略了也可以作為“學具”的重要功能,在實驗探究中,離不開數學的計算推理、邏輯證明,在這些過程中,可以有效培養學生的學習興趣,提高學生的數學核心素養.

4.3 本手、妙手的啟示

“本手”、“妙手”、“俗手”在現實生活中普遍存在,對于那些身處學習階段的孩子而言也是如此.“本手”為本分的一手,“俗手”意為庸俗的一手,“妙手”意為卓越的一手,可遇不可求,想下出真正的“妙手”,必須在平日有一定的經驗積累和訓練才可能完成真正卓越的“妙手”.

此題的“妙手”在于不聯立直線和拋物線而巧妙的設點,不拘泥于常規套路,抓住圖形的幾何特征,使得計算過程得到簡化! 一般而言,多數“妙手”具有反思、創新、批評與質疑等特質,也更讓人感嘆數學的數形結合之美! 而借助GeoGebra,能更生動的呈現“數與形的完美結合”!