考慮注意力機制的CNN-LSTM高滲透風電并網暫態電壓穩定性研究

張紅穎，賈一超，汪江志，張巍

（1.中國電力科學研究院有限公司，江蘇 南京 210037；2.上海理工大學機械工程學院，上海 200093）

0 引言

在低碳綠色發展的背景下，風能作為一種清潔能源，其資源量和環境友好的特性具有化石能源無法比擬的優勢。風能必將逐步成為化石能源的替代品，為實現“雙碳”目標和促進國民經濟低碳綠色發展提供堅實的保障[1]。風電的裝機容量在電力系統中的占比不斷提高，風能的間斷性和隨機性，以及不同風電機組間的強耦合和非線性特性，使得風電并網系統的運行條件和特性較傳統火電并網系統更加復雜，對電力系統暫態電壓穩定性帶來了嚴重挑戰[2]。

20世紀80年代末，機器學習方法逐步在電力系統暫態穩定評估問題中得到推廣使用。隨著廣域測量技術的發展和人工智能技術的成熟，基于人工智能的方法為大電網數據的智能分析提供了新的途徑。已有相關研究采用神經網絡進行暫態穩定評估，導致大量信息浪費。研究人員針對如何最大限度地發揮單一神經網絡的優勢，提高人工智能暫態穩定評估方法的實用性展開了大量研究。文獻[3]基于BP神經網絡模型，利用故障前后采集的傳統物理量和與風電場相關的物理量，作為輸入特征量進行監督學習，該模型最終可應用于評估風電并網系統的暫態電壓穩定性。文獻[4]提出了一種基于grcForest模型的方法，用于風電并網系統的暫態電壓穩定性評估。盡管這種方法在提高評估準確性和速度方面有一定改進，但仍須要進一步優化。文獻[5]提出了一種基于一維卷積神經網絡的暫態電壓穩定性評估方法，該方法利用卷積神經網絡提取特征，通過輸入特征和評估結果之間的映射關系來建立評估模型。文獻[6]提出了一種基于時間卷積網絡和圖注意力網絡的方法用于暫態穩定性評估，該方法利用圖注意力網絡處理圖數據，并建立電網拓撲連接關系，以提取空間特征和時間特征，在不完全配置條件下，圖注意力網絡的泛化能力較弱。已有研究大多關注系統暫態功角穩定性評估，對于暫態電壓穩定性評估研究還不夠充分，涉及到高比例風電接入的暫態電壓穩定性評估的研究更加匱乏，同時大多數研究都只停留于暫態穩定性評估，并未提出相應的改進措施[7，8]。

電網電壓發生驟降時，采用風電暫態電壓主動支撐技術可以支撐電網電壓[9]，確保風電機組及風電場在低電壓穿越時不脫網。然而，改變系統結構參數以限制電壓降落的成本高昂，而且會影響并網系統的穩定運行。此外，電抗器、高阻抗變壓器等設備接入會增加系統網損，從而對系統的穩定性產生不利影響[10]。使用故障電流限制器是解決風電系統故障電壓越限問題的有效方案，該裝置可以顯著提高風電機組的低電壓穿越能力，并為雙饋風電暫態電壓主動支撐技術的應用提供有力保障[11]。

為進一步評估系統受擾后的暫態穩定性，本文基于注意力機制提出一種CNN-LSTM暫態穩定性評估模型，針對暫態電流越限問題提出安裝超導短路限流器的主動支撐措施，改善風電場系統無功環境，維持并網點電壓穩定。最后，在PSD-BPA中搭建含風電的IEEE39節點系統進行仿真模擬和數據收集用于模型訓練。結果表明，本文所提評估指標具有更高的識別率，所提改進措施對提高系統暫態穩定性具有積極作用。

1 CNN-LSTM-Attention暫態穩定性評估模型

在實際工程中，通過判斷持續時間是否超過給定值來評估暫態電壓的穩定性，該持續時間是指暫態電壓偏移某一閾值的時間。隨著人工智能技術的迅速發展，在電力系統暫態穩定性評估中廣泛采用了機器學習和模糊邏輯技術等方法。

1.1 特征選取降維

在電力系統暫態穩定性評估中，樣本數據即為學習模型的輸入，樣本數據x可表示為D為樣本個數，n為特征數。

本文從時間、空間、系統規模的角度選取了28組原始特征，如表1所示。

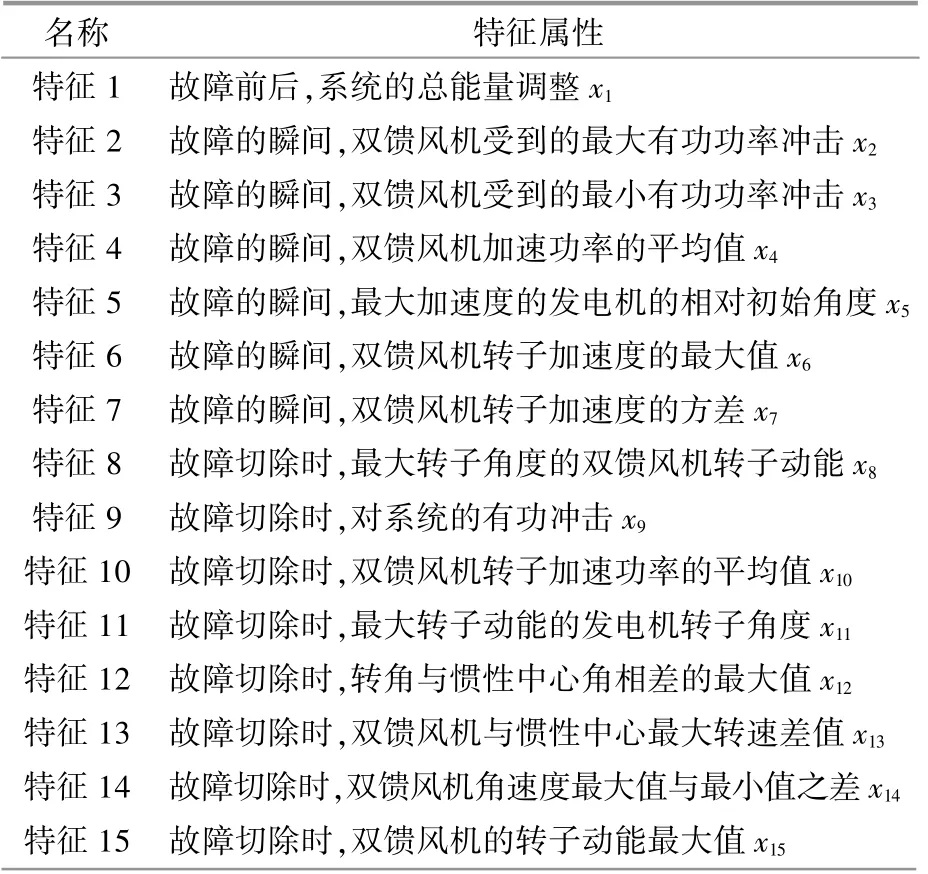
表1 原始特征集Table 1 Original feature set

電力系統是一個復雜的非線性系統，高比例風電接入電網進一步增加了系統的復雜度，采用傳統線性方法進行數據處理計算效率低下。因此，本文考慮采用非線性降維方法對輸入特征進行降維。核主成分分析（KPCA）是一種非線性數據處理方法，其核心思想是通過非線性映射將原始空間中的數據投影到高維特征空間，然后在該特征空間中采用主成分分析（PCA）進行數據處理[12]。

給定樣本矩陣x，x為D維列向量，共n個樣本，D×n維矩陣所在的空間稱為輸入空間，引入非線性變換φ將輸入空間映射到高維特征空間，這個高維空間稱為特征空間Γ，對Γ進行KPCA降維，定義協方差矩陣CΓ如下：

求解協方差矩陣的特征值λ和特征向量V：

將式（2）乘以φ（x），利用主成分應用系數αi=[α1，α2…，αn]T將V線性表示為

引入K為n×n維正半定核矩陣，高斯徑向基核函數計算方法簡單，分類效果好，因此本文采用高斯徑向基核函數作為核主成分分析的核函數[13]。

式中：i=1，2，…，n；j=1，2，…，n；σ為函數跌落到零的速度，取值0.5。

將K=φ（x）Tφ（x）代入式（3）得：

通過對式（5）進行求解，得到特征值問題的非零特征值和矩陣K的第k個特征向量，利用式（6）求解特征空間主元方向，即特征向量。

將式（6）代入式（3）可求解出對應的特征值λk，對特征值進行降序排序，確定主成分個數后根據排列順序選取對應主成分特征，形成降維特征集。采用累計方差貢獻率確定主成分個數：

1.2 通道注意力機制

CNN具有參數共享、局部感知的特點，能夠快速且精準地提取樣本特征，獲取更多隱藏特征信息，但在處理較長時間序列時效果不佳。LSTM作為CNN的變種模型，通過遺傳門、輸入門、輸出門的結構，能夠有效記憶長時間序列信息，通過聯系前后信息的特征得到更多數據。兩個神經網絡對于時序數據的非線性問題均有較好的處理能力，處理方式與結果各有優勢。為了提升模型的性能，本文將CNN與LSTM串聯結合，形成CNNLSTM模型，該模型能夠精準提取暫態特征并且可以有效解決學習時序數據中長期依賴信息的問題。但是在訓練該模型時，會忽略各通道信息的重要程度，造成資源分布不均，分辨效果下降[14]。因此，本文將注意力機制引入模型，通過注意力機制并根據重要程度對CNN中各輸出特征通道賦予不同的權重系數，對LSTM下各時序特征賦予不同的權重系數，保證序列長度增加時，重要特征不會丟失，以此實現分辨準確率的提升。本文在訓練模型時選用了通道注意力機制（Channel Attention Module，CAM）[15]，該機制主要是通過網絡訓練得到的損失值（Loss）來不斷學習更新特征權重，通過了解到的每個特征面的重要程度，根據重要性依次給每個特征通道賦予權重值，重要性強的特征面權重大，重要性弱的特征面權重小，從而使得有限的神經網絡用于計算有效特征面，減少參數與計算量。通道注意力機制的具體結構如圖1所示。

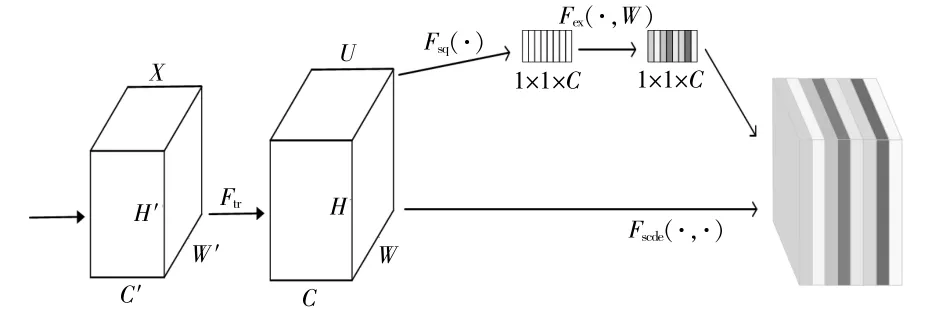
圖1 通道注意力機制具體結構Fig.1 The specific structure of the channel attention mechanism

由圖1可知，一個H′×W′×C′的特征圖X在經過卷積操作后變為一個H×W×C的特征圖U，特征圖U經過Sequeeze操作后變為一個1×1×C的矩陣，然后再經過Excitation操作，根據重要度給每一個特征通道賦予相應的權重值，最后被賦予權重的1×1×C矩陣與特征圖U經過Sigmoid函數將權重變量進行歸一化變換，如式（8）所示。對原始輸入特征圖賦予權重后可得到新的特征圖。

式中：p為歸一化前的權重變量。

1.3 模型評估標準

制定模型評估標準時，須要考慮實際電力系統中“漏判”和“誤判”對電力系統的影響。因此，模型評估方法指標除了整體的分辨準確率PAC外，還須要引入漏判率PMD和誤判率PFA，PMD和PFA，分別用于評估模型對穩定樣本和失穩樣本的分辨能力。

①準確率PAC：正確評估的樣本數占總樣本的百分比。

②漏判率PMD：真實失穩樣本被錯誤判定為穩定樣本的數量占真實失穩樣本總數的百分比。

③誤判率PFA：真實穩定樣本被錯誤判定為失穩樣本的數量占真實穩定樣本總數的百分比。

式中：TP表示正確預測為穩定的真實穩定樣本數量；FN表示錯誤預測為失穩的真實穩定樣本數量；FP表示錯誤預測為穩定的真實失穩樣本數量；TN表示正確判斷為失穩的真實失穩樣本數量。

1.4 暫態穩定評估算法流程

CNN-LSTM-Attention暫態穩定評估模型對電力系統暫態穩定性進行評估的算法流程如圖2所示。通過PSD-BPA軟件進行時域仿真收集數據集，這些數據經KPCA降維后的優選特征集將作為神經網絡的輸入特征。通過CNN層進行特征提取與深度挖掘后，利用Dropout層丟棄部分無用參數，再利用池化層對輸入特征進一步壓縮提取。將輸出特征傳入LSTM層，進一步提煉數據與時間之間的相關性，不斷調整參數，解決時序數據中長期依賴信息的問題。在完成CNN-LSTM串聯連接后接入自注意力機制層，根據重要程度對不同的特征賦值，最終通過全連接層輸出分解結果。由于本文為二分類研究，因此采取Sigmoid作為激活函數，可將輸出結果映射為（0，1）的概率分布，用于表示暫態穩定性評估結果。

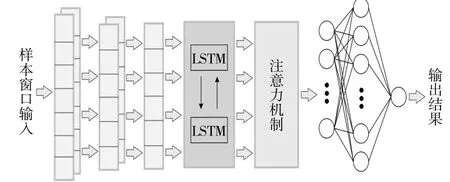
圖2 暫態電壓穩定評估流程Fig.2 Transient voltage stability evaluation process

2 暫態電壓穩定性機理及控制措施

2.1 風電并網影響系統暫態電壓穩定性的機理

當高比例風電接入的送端電網系統發生故障時，暫態電壓的變化程度與系統的短路容量密切相關。目前的研究普遍認為，高比例的新能源電網呈現出“弱電網”現象，因為大量的新能源電源取代了同步發電機，從而導致整個系統的短路容量降低。高比例風電接入的送端電網的抗擾動能力較差，電網的強度也較弱。雙饋風機作為目前采用的主要風機類型，其主體是異步電機，雙饋風機的短路容量計算式為

式中：UN為發電機平均額定電壓；IN為額定電流；Sam為電機等效容量；xk為短路電抗。

在工程設計中，異步電機的短路電抗越大，其提供的短路容量就越小。因此，在高比例的新能源電網中，整個系統的短路容量會下降，在相同程度的無功波動條件下，高比例風電接入的系統母線暫態電壓波動幅度也會更大。

2.2 故障限流器模型

電力系統的迅猛發展導致其規模不斷擴大，互聯程度越來越高，這使得短路電流水平不斷攀升，極大地影響了系統的安全運行。已有研究表明，在出現故障時，使用超導故障限流器可以有效維護機組無功功率輸出能力。因此，在解決風電系統過載問題方面，應用超導故障限流器是一個有效的解決方案。圖3顯示了理想條件下單機無窮大系統超導故障限流器接入模型示意圖[16]。

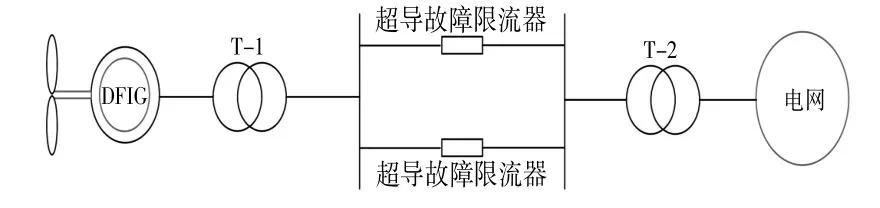
圖3 超導故障限流器布置示意圖Fig.3 Superconducting fault current limiter layout diagram

當系統正常運行時，發電機通過變壓器和雙回線路將電力輸送至無限大系統。當系統發生短路故障時，超導故障限流器中的超導體進行“自動變阻”。為了簡化分析，忽略超導故障限流器的電阻，只考慮其電抗的作用。假設發生短路故障時，投入系統的超導故障限流器的電抗標幺值為X。考慮到故障發生時，非故障線路上的故障限流器也會被觸發，因此，超導故障限流器可表示為如圖4所示的等效電路。

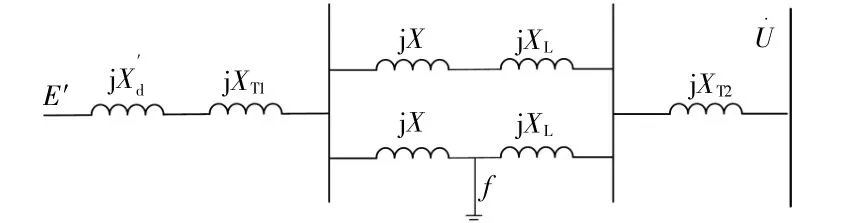
圖4 系統正常運行時超導故障限流器等效電路Fig.4 Equivalent circuit of superconducting fault current limiter in normal operation

經過星-角變換后得到化簡電路，如圖5所示。

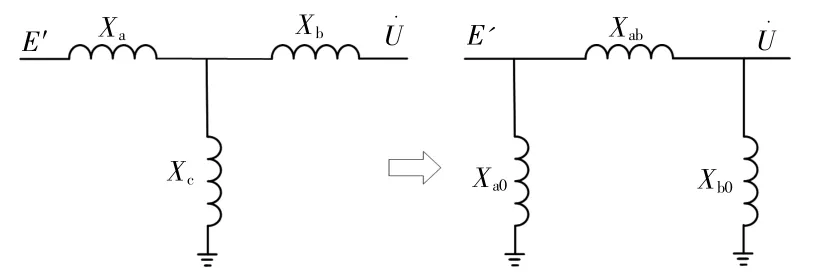
圖5 化簡等值電路Fig.5 Simplified equivalent circuit

當系統發生三相短路時，XΔ≈0，系統的轉移阻抗可以表示為SFCL投入電抗值的函數f（X）。隨著SFCL投入系統電抗值的增加，系統的總轉移阻抗會減小，并最終趨于一個穩定值。當X趨近于零時，轉移阻抗將趨近于無窮大。因此，當系統發生短路時，超導限流器投入阻抗以減小系統的總轉移阻抗，從而提高PII幅值，有助于提升系統的暫態穩定性。

3 算例分析

本文采用中國電科院暫態仿真軟件PSDBPA作為仿真平臺，構建了如圖6所示的英格蘭10機39節點電力系統的仿真模型。仿真參數見表2。基準功率設定為100 MW，基準電壓為345 kV。為進一步研究風電并網對系統暫態電壓穩定性的影響，將25臺1.5 MW的風電機組等效成一個群體，接入到電網中。該風電機組的額定電壓為0.69 kV，經升壓變壓器升高后連接到37號節點。通過潮流計算和時域仿真，共獲得1 986個樣本，其中包括1 330個穩定樣本和656個失穩樣本。

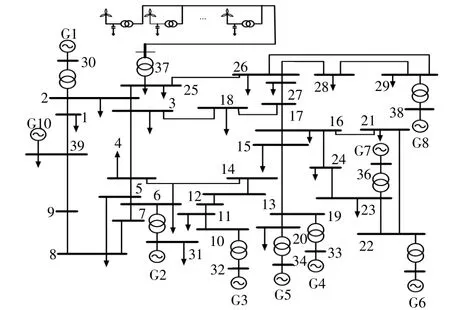
圖6 風機接入IEEE39節點系統拓撲圖Fig.6 Topology of the fan connected to the IEEE39 nodes

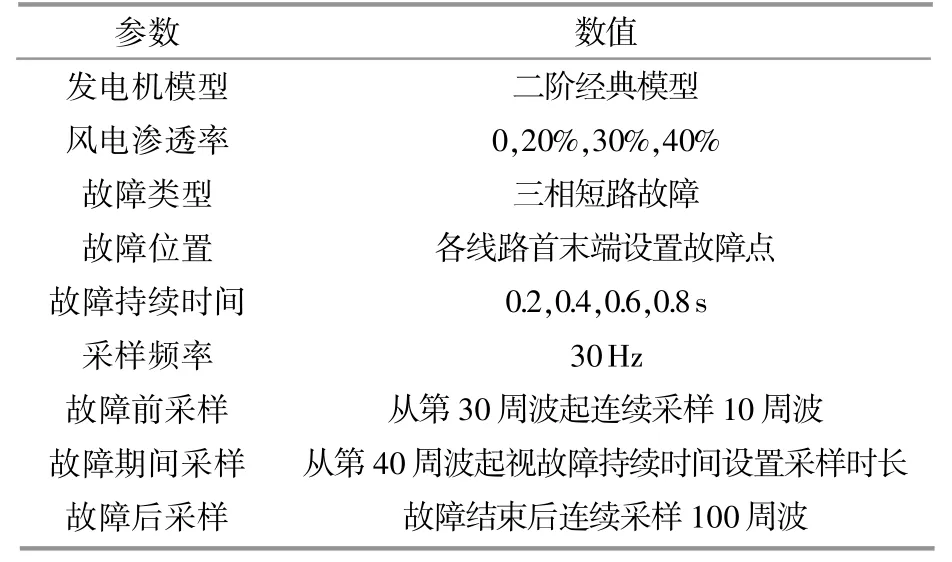
表2 新英格蘭39節點系統仿真算例的樣本數據構造方法Table 2 Sample data construction method of New England 39-bus system simulation example

3.1 KPCA特征降維

利用KPCA算法對采集得到的28維特征數據共計1 986個樣本進行特征降維分析，當累積方差貢獻率≥99%時，優選特征向量即可代表所有特征向量。表3為13個主成分的特征值、累積方差貢獻率。

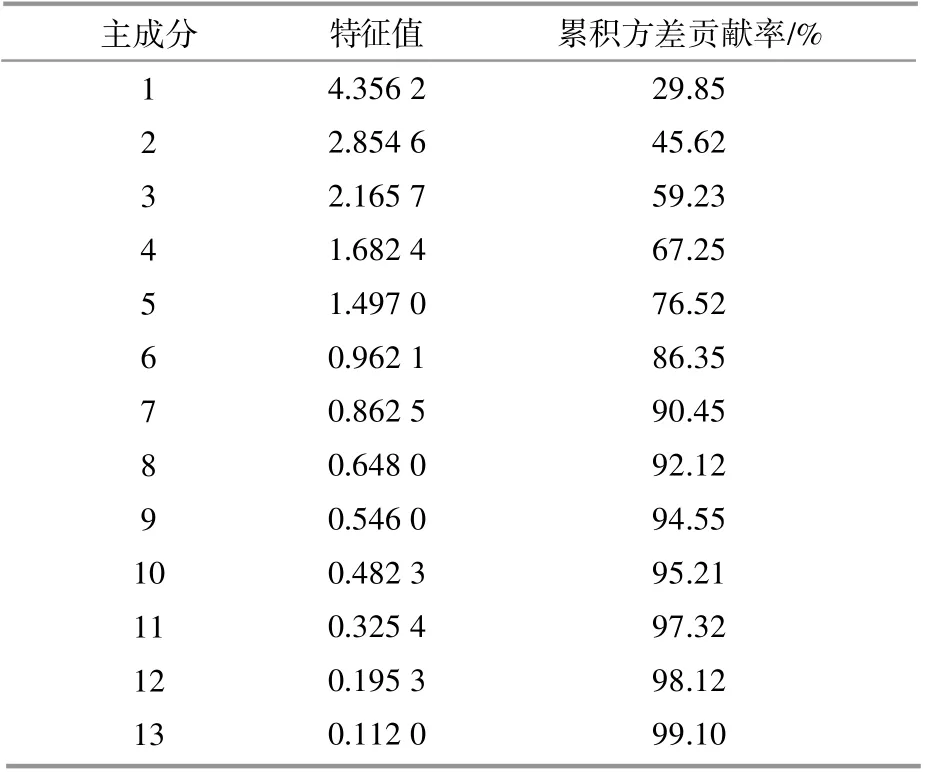
表3 主成分分析Table 3 Principal component analysis table

由表3可知，主成分累計方差貢獻率已經達到99%，說明前13個主成分完全可以替代所有主成分作為暫態電壓穩定評估的輸入特征集。通過對各個主成分與其對應的特征值進行排序選取前13個特征，可以得到表4中所示的優選特征。

表4 優選降維特征集Table 4 Preferred downwitter solicitation

3.2 失穩判據

每一個樣本數據Xi（i=1，2，…，n）都有一個對應的標記Yi=[Y1，Y2，…，Yn]，當Yi取1時標記為穩定，當Yi取0時標記為失穩。

仿真過程中，采用符合《風電場接入電網技術規定（GB/T19963-2011）》的風電并網系統暫態電壓穩定性評判準則。該準則規定，在發生大幅度擾動情況下，系統側母線電壓低于0.75 p.u.的時間不得超過1.0 s，且雙饋風機的功角必須保持穩定，否則將被判定為暫態不穩定。

圖7所示為系統在0.1 s發生三相短路故障時系統母線電壓幅值。從圖7中可以看出，在發生故障期間，系統母線電壓發生了劇烈的變化。當故障清除時間較短時，系統可以通過自我調節保持暫態電壓穩定。但是，當故障清除時間較長時，系統無法維持暫態電壓的穩定，如圖8所示。

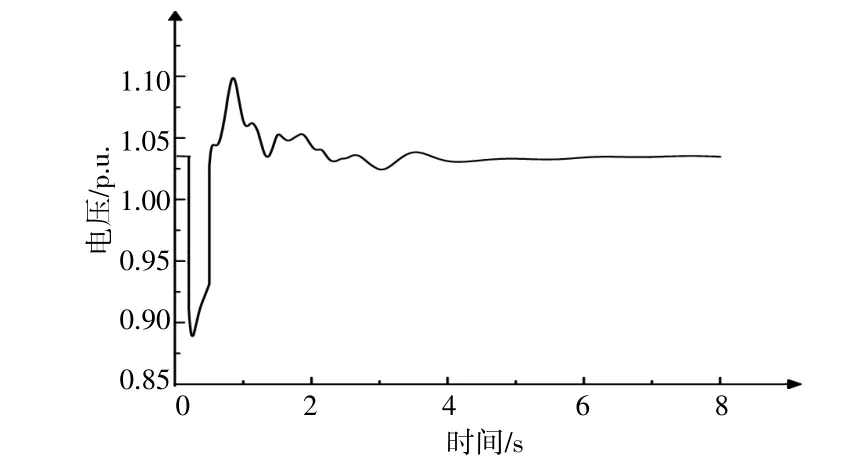
圖7 大擾動情況下暫態電壓穩定性Fig.7 Transient voltage stability under large disturbance

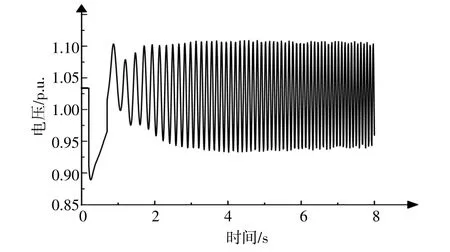
圖8 大擾動情況下暫態電壓不穩定性Fig.8 Transient voltage instability under large disturbance

3.3 結果分析

為了能更加直觀地體現模型對電力系統暫態穩定性的評估性能，本文將同樣的優選特征訓練樣本分別輸入到CNN，LSTM模型中，進行訓練并測試模型的評估性能。其中，LSTM和CNN的結構參數和本節提出的CNN-LSTM-Attention一致，其他模型結構參數均通過網格搜索法找出最優的超參數。各評估模型的測試結果如圖9所示。

圖9 各評估模型分辨準確率測試結果Fig.9 Test results of the estimated model

由圖9可知：當訓練到30輪以后，CNNLSTM-Attention準確率更高且趨于收斂，其余模型在訓練40輪以后才趨于收斂并且后續準確率波動較大；CNN-LSTM-Attention模型的分辨準確率PAC最高，漏判率PMD最低，這與該模型能夠精準提取暫態特征并且可以有效解決學習時序數據中長期依賴信息的問題密不可分。同時利用注意力機制并根據重要程度對CNN中各輸出特征通道賦予不同的權重系數，對LSTM下各時序特征賦予不同的權重系數，保證序列長度增加時，重要特征不會丟失。預測結果表明，引入注意力機制能更好地保留重要特征用于模型訓練，更精準地提取使用關鍵的特征，CNN-LSTM-Attention比CNN-LSTM的分辨準確率高0.98%，漏判率降低了2%。

為了驗證本文雙饋風機對電力系統暫態電壓穩定性的影響以及構建的附加超導故障限流器對電力系統暫態穩定性的積極作用，設置如表5所示的不同滲透率及發生不同程度的負荷擾動共10個場景進行仿真分析。

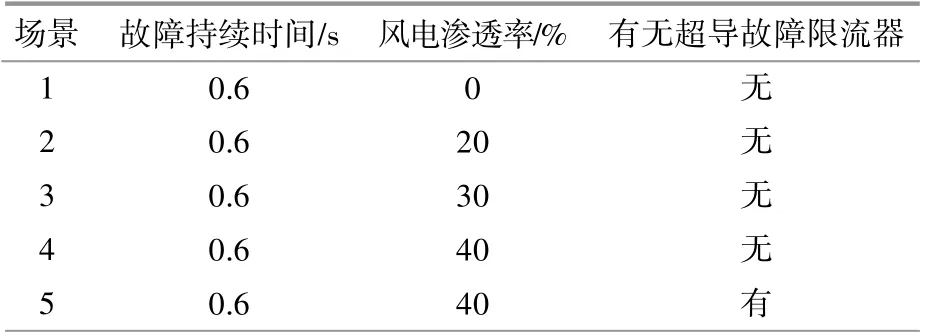
表5 不同滲透率仿真場景Table 5 Simulation scenarios of different permeability rates

為了驗證不同風電滲透率對系統暫態電壓穩定性的影響，在相同故障持續時間下，在25節點處引入短路故障進行仿真分析。短路類型從金屬性故障轉化為三相非金屬性短路故障，并在故障發生后的0.6 s被完全切除。通過仿真獲得了風電滲透率為0%，20%，30%，40%時風電并網系統的運行情況，分析了不同風電滲透率下的系統暫態電壓穩定性。分別提取不同風電滲透率下的優選特征參數，代入訓練好的CNN-LSTM-Attention模型進行暫態評估，結果如表6所示。

表6 不同風電滲透率評估結果Table 6 Evaluation results of different wind power permeability

由表6可以看出，在場景1～4中，在沒有超導故障限流器的情況下，隨著風電滲透率不斷增大，電網的無功需求隨之增多，電網靜態電壓穩定裕度不足的問題凸顯。當風電滲透率達到40%時，系統并網母線電壓發生嚴重跌落且不具備回穩能力，系統發生暫態電壓失穩現象。對比場景4和場景5，在故障發生瞬間超導故障限流器介入工作，故障限流器會立刻投入高阻抗來抑制系統短路電流，提高短路容量，進一步提高系統暫態穩定能力。當故障切除時，故障限流器不呈現阻抗，不會對線路的傳輸容量造成任何影響。

本文還驗證了不同故障持續時間下系統的暫態電壓穩定性。故障擾動過程：0 s時在25節點處發生三相金屬性短路，0.1 s時故障發展為三相非金屬性短路故障。在不同故障持續時間下，分別提取不同風電滲透率下的優選特征參數，代入訓練好的CNN-LSTM-Attention模型進行暫態評估，結果如表7所示。

表7 有無超導故障限流器評估結果Table 7 Evaluation results of current limiter with or without superconducting fault

對比場景6，7可以看出，當系統故障切除時間小于0.6 s時，系統中樞母線電壓及風電并網母線電壓波動相對較小，系統仍處于穩定狀態。當故障切除時間延長至0.6 s時，系統中樞母線電壓將發生嚴重跌落，系統由暫態穩定狀態過渡到暫態電壓失穩狀態。隨著故障持續時間的延長，系統中樞母線及風電并網母線的電壓跌落程度越發嚴重。對比場景9，10可以看出，超導故障限流器在一定限度內能支撐嚴重故障。

4 結論

本文基于自注意力機制提出了一種CNNLSTM暫態穩定評估指標，為更好地捕捉輸入數據中的空間和時間相關性，基于核主成分分析（KPCA）進行特征降維；針對暫態電壓突出問題提出安裝超導故障限流器的主動支撐措施，改善風電場系統無功環境，維持并網點電壓穩定。在PSD-BPA中搭建含風電的IEEE39節點系統進行仿真計算和數據采集，得到如下結論。

①核主成分分析（KPCA）方法能夠有效地篩選電力系統暫態穩定性評估中重要度高的特征，前13個主成分完全可以替代所有主成分，作為風電并網暫態電壓穩定性評估的輸入特征集，明顯地縮短了風電并網系統暫態電壓穩定性評估的計算時間。

②與目前一些淺層的神經網絡和深度學習網絡相比，本文所提出的CNN-LSTM-Attention網絡能有效提高電力系統暫態穩定性評估性能。CNN-LSTM可以充分利用時間序列變量的信息，注意力機制也能夠有效地挖掘數據信息。

③隨著故障持續時間的不斷延長，系統中樞母線及風電并網母線的電壓跌落程度越發嚴重，超導故障限流器在一定限度內能支撐嚴重故障，對系統暫態電壓的穩定具有積極作用。