考慮可再生能源出力不確定性與碳排放成本的臺區運行優化策略研究

王建波，秋澤楷，張小慶，豆敏娜，劉嘯，盧俞帆，呂錫林，王儷蓉

（1.國網陜西省電力有限公司電力科學研究院，陜西 西安 710100；2.華北電力大學，北京 102206）

0 引言

隨著金融行業的發展和電網公司的市場化改革，各類社會資本將逐步涌入電力市場，配電網下轄的臺區和配電網本身都將隸屬于不同的利益主體，各利益主體為了追求最大的自身利益相互競爭，形成多主體博弈格局。本文建立了由配電網運營商和其下轄的臺區構成的一主多從博弈模型，實現各主體之間的利益均衡。首先運營商制定動態電價，然后各臺區對電價做出響應，合理制定內部分布式電源出力以及與運營商的能量交易。

在“雙碳”背景下，我國能源結構清潔化轉型步伐日益加快，大量分布式能源（Distributed Energy Resources，DER）接入配電網臺區（Transformer District，TD），提升了配電網能源構成清潔性的同時，源側不確定性也使配電網調度運行風險進一步提升。目前，為降低不確定性影響，實現分布式可再生能源有效分層調控，將同一配電TD下的分布式可再生能源機組、分布式火電機組、儲能以及部分可平移負荷作為整體進行統一調控[1]，在TD內部優先平抑可再生能源出力的不確定性[2]。

相關研究基于馬爾科夫[3]、Coulpa[4]和ARMA[5]等方法生成可再生能源預測出力曲線[6]，本文采用蒙特卡羅法生成風光出力的預測曲線。由于可再生能源出力具有不確定性，預測出力曲線與實際出力曲線存在誤差，導致出現棄風棄光的風險。目前，已有較多研究將條件風險價值（Conditional Value at Risk，CVaR）理論用于量化可再生能源不確定性所造成的運行風險。文獻[7]運用CVaR理論度量風電不確定性引發的調度風險，建立了基于CVaR含碳捕集電廠與風電的電力系統的綜合低碳優化調度模型。文獻[8]運用CVaR理論量化虛擬電廠內分布式光伏發電的不確定性，構建了計及光伏出力不確定性的一主多從日前優化調度模型。文獻[9]運用CVaR理論度量綜合能源系統中源荷兩側的不確定性，建立考慮電源側的風、光出力和負荷側不確定性的綜合能源經濟調度模型。文獻[10]利用魯棒優化論（Robust Optimization，RO）和CVaR理論描述風光出力不確定性風險，構建虛擬電廠規避運行風險優化模型。本文基于上述研究，運用CVaR理論量化TD內棄風、棄光風險。

目前，為控制全球“溫室效應”進一步加劇，已有多國建立了碳排放權交易市場，截至2022年1月，全球共有25個碳市場正在運行，還有22個碳市場正在建設或準備建設中[11]。為實現“雙碳”目標，我國構建了碳排放權交易體系，引入了碳排放配額。碳配額的分配方式主要分為有償、無償分配兩種，為刺激碳市場交易，通常采用基于基準線的無償分配方式為各參與主體分配碳配額。文獻[12]將碳交易成本作為風光火儲系統優化目標之一，構建了碳交易與碳捕捉成本達到均衡的碳排放調度模型。

配電網中高比例可再生能源的接入雖造成了不確定性風險，卻能夠有效降低碳排放，進一步實現能源清潔化轉型。因此，亟需在可再生能源出力的不確定性風險與清潔性收益間找到平衡，在規避不確定風險的同時降低TD內的碳排放量。本文將各TD主體在碳市場交易中的收益加入配電網運營商（Distribution System Operator，DSO）收益的目標函數，以量化發電的清潔成本，并在各TD的運行成本中加入不確定性導致的棄風、棄光風險成本。

綜上所述，本文在現有研究的基礎上，同時考慮了配電TD內的分布式可再生能源出力不確定性引起的調度風險和各TD主體的發電碳排放行為。首先，為協調DSO和其下轄TD之間的利益關系，建立了由DSO和其下轄的多個TD所構成的主從博弈模型；然后，通過引入CVaR理論量化可再生能源出力不確定性造成的運行風險；最后，通過BP神經網絡擬合將雙層主從博弈模型簡化為單層模型，并運用粒子群算法進行求解。

1 多臺區能量管理的主從博弈模型

為平抑分布式可再生能源出力的不確定性，將隸屬于同一配電TD的分布式光伏（PV）、風電（WT）、微型燃氣輪機（MT）、電能存儲裝置（ES）以及可中斷負載（Interruptible Load，IL）作為整體，以安全性和經濟性為目標，由DSO統一調控參與電力市場和碳市場交易。基于此，本文提出了一種DSO及其下轄TD的電量交易模式，如圖1所示。在每個時段內，TD與DSO的購售電價是由DSO實時制定的，然而該時段內的TD內部發電量和耗電量可能不平衡，若某TD對外呈現電量富余稱之為“富電TD”，若某TD對外呈現電量缺乏稱之為“缺電TD”，若某TD內部能夠實現供需平衡稱之為“平衡TD”。“富電TD”將多余電量按照售電價格賣給DSO，“缺電TD”則按照購電價格向DSO購買所需電量。DSO根據各TD電量的供求狀況，通過購售電價與主網進行電能交易，實現配電網的能量供需平衡，并在該過程通過電價差價賺取收益。

圖1 DSO與TD的電量交易關系Fig.1 Relationship of exchange energy between DSO and TD

除此之外，DSO帶領所轄TD參與碳市場交易，火電機組發電量參與碳配額交易[11]；可再生能源發電商在碳交易市場中通過出售國家核證自愿減排量（Chinese Certified Emission Reduction，CCER）獲利[13]。DSO通過協調所轄TD的分布式火電與可再生能源發電設備出力使其自身在電碳市場的綜合收益最大。

由于DSO和TD屬于不同的利益主體，可將二者的主體分別視為博弈的領導者和跟隨者，如圖2所示。在此交易模式結構中，作為領導者的DSO能夠制定與各TD的電量交易價格，制定電價之前DSO須要收集其下轄所有TD提交的購售電量數據，結合電力市場的購售電價、碳市場的碳價及碳配額總量，合理制定其與TD間的交易電價，以實現自身收益最大化。各TD則作為跟隨者，根據DSO設定的交易電價，進一步考慮風光出力的不確定性所帶來的運行風險和清潔能源補貼所帶來的收益，以降低自身綜合運營成本為目標，調整自身內部的DER和負荷的發用電量。

圖2 主從博弈框圖Fig.2 Framework of stackelberg game mode

1.1 領導者效用模型

1.1.1 效用函數

DSO作為主從博弈的領導者，以最大化自身收益為效用函數，如式（1）所示。此處收益包括DSO參與電力市場能量交易的收益、DSO參與碳交易市場的收益和DSO與各TD交易的收益。

CCAR的計算方法如式（4）～（6）所示。

式中：CFP為分布式火電機組參與碳配額交易的收益；CRP為可再生能源發電商出售CCER的收益；λC為碳價；γref為單位電量的碳排放配額；γj，i為第j個TD內的第i個MT的碳排放系數；為t時刻第j個TD內的第i個MT發出的有功功率；λCCER為碳市場內單位CCER的交易價格；分別為第j個TD內的第m個WT和第n個PV的發電量與CCER的轉換系數[13]；分別為第j個TD內的第m個WT和第n個PV發出的有功功率。

1.1.2 約束條件

DSO在制定與TD交易的購售電價時，應滿足如下約束：

滿足上述約束可確保各TD在最小化綜合運行成本時優先選擇與DSO交易，而非直接向主網購售電。由式（7）可以確定DSO制定的策略空間ΩDSO，如式（8）所示。

1.2 跟隨者效用模型

TD根據DSO制定的購售電價和碳配額做出響應，確定其內部的各DER出力以及與DSO的交易電量，追求自身利益最大化，如圖3所示。

圖3 TD響應機制Fig.3 Respond mechanism of TD

1.2.1 效用函數

在主從博弈中，作為跟隨者的TD以最小化全時段內自身運行成本為目標函數，如式（9）所示。

式中：ai，bi，ci為t時段第j個TD中第i個MT的發電成本系數；第j個TD中第k個ES的調度成本系數；第j個TD中第m個WT發電成本系數；為第j個TD中第n個PV的發電成本系數；為第j個TD中第r個IL的中斷補償電價。

1.2.2 臺區棄風、棄光成本

CVaR是基于風險價值（Value at Risk，VaR）演變而來的一種風險分析方法[14]，與常規的風險度量方法如VaR、敏感度分析法（Sensitive Analysis，SA）[15]相比，CVaR在預測“尾部風險”[16，17]、保持正齊次性和傳遞不變性方面表現出明顯的優勢。本文運用CVaR理論研究TD內由風光出力不確定性所引起的棄風、棄光風險成本。

首先，通過風光出力偏差來衡量不確定性造成的運行損失，構造損失函數如下：

出力偏差過大會導致棄風、棄光量增加，設上述出力偏差不超過一定閾值α的概率為函數如式（17），（18）所示。

在給定的置信水平β下，根據VaR理論的定義，構造風光出力偏差的VaR值，如式（19），（20）所示。

在VaR的基礎上，進一步計算風光出力偏差的CVaR值，如式（21），（22）所示。

式中：σm，σn分別為第m個WT機組和第n個PV的棄風、棄光成本系數。

1.2.3 約束條件

在響應DSO設定的電量交易價格的同時，TD必須確保內部功率平衡，各DER也要滿足各自的運行約束。

式中：式（29）為t時段內第j個TD的功率平衡約束；式（30），（31）分別為TD與DSO的能量交易約束；為第j個TD與DSO的交易電量；θj，t為布爾變量，用于描述TD的購售電行為，θj，t=1時表示在t時段第j個TD向DSO售電，θj，t=0表示TD向DSO購電；為第j個TD與DSO交易的最大電量；式（32）為MT運行約束；為t時段第j個TD中的第i個MT的最大輸出功率；，分別為MT向下、向上的爬坡率；式（33）為t時段第j個TD中的第k個ES的運行約束；為t時段ES的荷電狀態；分別為荷電狀態的上、下限值；分別為ES充放電功率的上、下限值；Ek，max為ES最大能量容量值；式（34）為IL的中斷電量約束；為t時段第j個TD中的第r個IL的最大中斷量；式（35）為WT的運行約束；為t時段第j個TD中的第m個WT的最大輸出功率；式（36）為PV的運行約束；為t時段第j個TD中的第n個PV的最大輸出功率。

1.3 主從博弈模型

由DSO和TD構成的主從博弈模型可記為

若在對方現有策略的影響下，領導者與跟隨者雙方都無法通過改變策略來提升自己的收益時，主從博弈到達平衡點。

式（38）也可記為雙層形式：

2 主從博弈模型求解

主從博弈模型通常有兩類求解方法：一類是傳統的數學方法，即通過KKT條件將雙層模型轉換成單層模型，但在本文的主從博弈模型中，由于式（31）中含有布爾變量θj，t，導致該方法不適用；另一類方法是直接采用啟發式算法求解雙層模型[18]，這類方法求解過程往往過于復雜，求解時間較長。

BP神經網絡（Back-Propagation Neural Network，BPNN）能學習和存貯大量的輸入-輸出模式映射關系，無需事前揭示描述這種映射關系的數學方程。BPNN在處理函數逼近問題時，直接利用樣本數據來實現輸入和輸出的非線性映射，在樣本數據中自動逼近最佳刻畫樣本數據規律性的函數。因此，本文提出了一種BPNN結合粒子群算法的主從博弈均衡解求解算法，采用BPNN擬合并取代TD內部的能量管理模型，有效地避免了上述兩種方法的弊端。

2.1 用BPNN建立擬合模型

本文所構建的BPNN輸入層的物理量為T個時段的售電價λTD，s和購電價λTD，b，輸出層的物理量為T個時段的各TD與DSO的交易電量，隱含層的層數為單層，最終得到輸入輸出參數的映射關系，如式（40）所示。

式（39）的主從博弈模型可轉換為單層模型，如式（41）所示，其中購售電價λTD，b，λTD，s為模型決策變量。

2.2 主從博弈均衡解求解算法

本文采用了基于BPNN的主從博弈均衡解求解算法，其步驟如下。

步驟1：初始化系統參數。對參數進行初步設定，包括DSO通過電力市場與主網進行能量交易的上網電價和電網電價、TD內部各DER的參數、主從博弈均衡解求解算法中BPNN和粒子群算法的參數等。

步驟2：場景生成。采用MCS法，基于風光出力的歷史數據，生成包含概率信息的風光出力預測值；采用拉丁超立方采樣（Latin Hypercube Sampling，LHS）法，基于現有電價數據，生成K個起始樣本點，記為中每個樣本點的兩個數值代表一組購售電價，如式（42）所示。

步驟6：將現有的樣本數據集Bj帶入式（1）中，得到每一組對應的上層目標函數值，即DSO在k場景下的收益。依據計算結果，將DSO的策略空間ΩDSO劃分為Nl個重要區間，每個關鍵區間的上層目標函數即DSO收益最優值記為。

步驟10：對各個區域的最優解進行比較，可得出當前循環的全局最優解，如式（45）所示。

步驟12：判斷是否達到迭代收斂標準，若達到迭代收斂標準，則停止迭代并輸出均衡解，否則返回步驟4。

3 算例分析

3.1 算例說明

本文構建了一個含有3個TD的仿真系統，每一個TD包含WT，PV，ES及MT等不同種類的DER，TD中的微型燃氣輪機參數如表1所示，儲能參數如表2所示，風光出力預測曲線如圖4所示，負荷曲線如圖5所示。

表1 微型燃氣輪機參數Table 1 Parameters for MT

圖4 風光出力預測曲線Fig.4 Prediction power of PV and WT

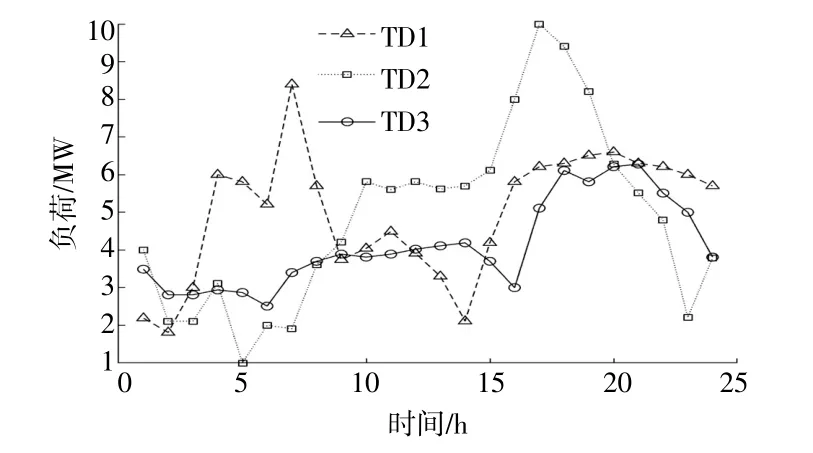
圖5 負荷預測曲線Fig.5 Prediction power of load

運用CPU為Core i9-12900HX，主頻為3.6 GHz，內存容量為16 GB的計算機進行優化仿真分析。運用matlab的yalmip+cplex工具包對所提下層模型進行優化求解。

3.2 仿真結果分析

本文設計了3種不同的場景以驗證上述模型的有效性。

①DSO不參與碳市場交易。在電力交易中DSO不控制電價，將DSO與TD的交易電價設置為主網的購售電價，各TD間采取非協作的競爭策略。

②DSO不參與碳市場交易。在電力交易中DSO通過對電價進行調整優化自身利益，DSO與各TD間采取主從博弈模式。

③DSO參與碳市場交易。在電力交易中DSO通過對電價進行調整優化自身利益，DSO與各TD間采取主從博弈模式。

3.2.1 場景1，2對比結果分析

在場景1，2下，DSO制定的各TD與DSO的交易電價如圖6所示。

圖6 交易電價Fig.6 Trading price

在圖6制定的電價下，各TD根據自身利益需求調整內部DER的出力。根據各時刻自身內部發電量和用電量是否平衡，可將TD劃分為“富電”、“缺電”和“平衡”3種狀態。在某個時刻，處于“富電”的TD會將富余的電量出售給DSO，以獲取收益，降低運行成本；處于“缺電”的TD會向DSO購買缺額的電量，以滿足自身負荷用電需求；處于“平衡”的TD不須購買或者出售電量。用交易電量的多少描述TD與DSO之間的能量交易，當TD向DSO購買電量時取值為正。當交易電量大于0時，表示該TD有功率缺額，向DSO購電；當交易電量小于0時，表示該TD電量富余，售電給DSO；當交易電量等于0時，表示該TD不與DSO進行能量交易。交易電量的9種取值情況分別對應上述TD的3種狀態。場景1，2下各TD與DSO交易電量如圖7所示，TD的3種狀態在圖7中得以表現。

圖7 場景1，2下各TD與DSO交易電量Fig.7 Trading power between TDs and DSO in subscenario 1 and 2

根據式（2），在對各TD與DSO交易的電量進行匯總后，DSO會根據下轄TD整體能否滿足功率平衡來判斷是否需要與電力市場進行電能交易。根據式（3），DSO與電力市場的交易電量即為各TD與DSO購電量之和減去售電量之和，因此可求出DSO與TD總交易電量。場景1，2下DSO與TD的交易電量如圖8（a）所示。DSO會優先將“富電”TD富余的電能出售給“缺電”TD以彌補缺額的電能，這部分來自于TD并通過DSO用于TD的電能即為TD之間的“共享電量”。在某時刻，當＞0時，共享電量為當＜0時，共享電量為。場景1，2下各TD之間的共享電量如圖8（b）所示。

圖8 場景1，2下DSO與所有TD的交易電量以及TD間的共享電量Fig.8 Trading power between DSO and all TDs and shared power between TDs

由圖7可以看出，在場景1的第2小時時段，TD1，TD2分別售出10 MW的電能給DSO。根據式（2）可得TD與DSO的交易電量為-20 MW，根據式（3）可得TD之間的共享電量為0 MW。在場景2下，TD1售出10 MW的電能給DSO，TD3從DSO購買了2.8 MW的電能。根據式（2）可得DSO與TD交易電量為-7.2 MW，根據式（3）可得TD之間的共享電量為2.8 MW。在場景1的第12小時時段，TD1售出10 MW的電能給DSO，TD2從DSO購買6 MW的電能。根據式（2）可得DSO與TD交易電量為-4 MW，根據式（3）可得TD之間的共享電量為6 MW。在場景2下，TD1售出10 MW的電能給DSO，TD2從DSO購買了6 MW的電能，TD3從DSO購買了4 MW的電能。根據式（2）可得DSO與TD交易電量為0 MW，根據式（3）可得TD之間的交易電量為-10 MW。以上結果可以從圖8得到驗證。

比較兩種場景的TD共享電量可以看出，在場景2下，TD響應DSO的動態電價并實施能源管理優化策略后，TD之間的共享電量與共享時長比場景1有顯著的增長。因此，DSO向電力市場購買的電量減少了，獲得的利潤有所增長。

場景1，2下DSO和TD的效益如表3所示。當數值為正時表示運行成本，為負時表示利潤。由表3可以看出，在場景2下，DSO能夠通過優化配電網內部交易電價，顯著提高自身的利潤；同時，因為DSO制定的內部購電價不會超過電力市場上的電網電價，內部售電價不低于電力市場上的上網電價，所以TD的成本費用也相應減少。

表3 場景1，2下TD和DSO的效益Table 3 Benefits of TD and DSO in Scenarios 1 and 2 千元

結合圖6～8，分析兩種場景下運營商制定的動態交易電價和各TD與DSO交易電量之間的關系，整體上可以分為以下3類情況。

第一類是完全供不應求，典型時段如20，21，22時段。在這些時段中3個TD均處于“缺電”的狀態，沒有多余的電能實現跨臺區共享。為了解決配網內電能不足的問題，DSO只能通過電力市場向主網購電，然后TD向DSO購電滿足自身需求。DSO為了減少損失，會制定較高的配網內售電價格，從圖6可以看出，這些時段的售電價均接近于電網電價。

第二類是整體供不應求，典型時段如15，16，17時段。在這些時段中存在多種狀態TD，但整體上還是供不應求，DSO仍然要向主網購電滿足需求。從圖6可以看出，此時DSO仍然會給TD制定較高的售電價格，但是比起第一類情況要低一些，同時還會制定較高的購電電價，引導“富電”TD多售電，滿足“缺電”TD需求，以減少DSO從電力市場購電。

第三類是整體供過于求，典型時段如1，2，10，11時段。在這些時段中同樣存在多種狀態TD，但整體上是供過于求，DSO會將多余電能賣到電力市場以獲取利益。由于此時電能充沛，DSO會制定較低的售電價格，吸引“缺電”TD和“平衡”TD購電，實現自身更多利益。

3.2.2 場景2，3對比結果分析

在場景2下，DSO未參與碳市場交易，此時尚未計及碳排放成本。在場景3下，由于DSO在電力交易的基礎上還參與了碳市場交易，需要在兼顧電能交易收益的同時兼顧發電的清潔成本，平衡電能需求與碳排放。本文分別設置了隸屬于場景3的3種子場景，各子場景對應的碳價λC和單位CCER的交易價格λCCER組合如表4所示。臺區1在場景2及場景3中子場景1～3對應的風電、光伏出力曲線分別如圖9，10所示，其余臺區內的風光出力見圖11～14。

表4 不同子場景下的碳價和單位CCER價格Table 4 The price of carbon and unit CCER in different sub-scenarios 元/t

圖9 不同場景下臺區1內WT功率曲線Fig.9 Power output curve under different scenarios of WT in DT1

由圖9可以看出，在3～9，15～24時段內，場景3的子場景3對應的風電出力最大，子場景1對應的風電出力最小。由表4可知，子場景3所對應的碳價λC最高，而單位CCER交易價格λCCER最低，造成該場景下臺區通過調用分布式MT發電的碳排放成本高，而通過調用分布式可再生能源發電在碳市場中可以獲得較多的補貼。因此，在子場景3下，臺區1傾向于調用分布式MT，PV發電，此現象同樣出現在其余臺區中，具體見圖11～14。由圖10可知，在6～9，15～19時段內，場景3的子場景3對應的光伏出力最大，子場景1對應的光伏出力最小，這一現象同樣是由上述原因所導致的。

圖10 不同場景下臺區1內PV功率曲線Fig.10 Power output curve under different scenarios of PV in DT1

圖11 不同場景下臺區2內WT功率曲線Fig.11 Power output curve under different scenarios of WT in DT2

圖12 不同場景下臺區2內PV功率曲線Fig.12 Power output curve under different scenarios of PV in DT2

圖13 不同場景下臺區3內WT功率曲線Fig.13 Power output curve under different scenarios of WT in DT3

圖14 不同場景下臺區3內PV功率曲線Fig.14 Power output curve under different scenarios of PV in DT3

由圖9，10還可以看出，在場景2下風光出力均小于場景3中各子場景下的風光出力，這是因為場景2中DSO不參與碳市場交易，未能調動各臺區內可再生能源出力的積極性。由此可見，參與碳市場交易有助于調整配電側分布式發電能源結構，刺激臺區調動內部清潔能源發電。由圖9可知，在1～2，10～14時段內，各場景下風電出力相同。而圖10顯示，在10～14時段內，各場景下光伏出力相同。這是由于在上述時段內，臺區1通過向DSO售電獲利，此時分布式可再生能源滿發以滿足臺區1向DSO售電的需求。

4 結論

針對配電側多臺區運行優化問題，本文構建了主從博弈模型，將DSO和所轄TD分別作為博弈的領導者與跟隨者，實現了領導、跟隨雙方利益的優化。針對分布式可再生能源出力的不確定性，本文采用CVaR理論進行量化，規避了風光出力不確定性造成的運行損失。此外，本文進一步將碳市場收益加入DSO效益模型，通過加入碳市場交易刺激所轄臺區內可再生能源出力，降低發電碳排放成本，實現電碳市場收益綜合優化。最后，通過算例驗證本文所建模型的有效性，得出以下結論。

①依托主從博弈模型，DSO能夠執行動態定價策略引導TD進行電能交易，并使雙方在此過程中均能獲得最大收益。

②通過運用CVaR模型量化可再生能源出力的不確定性，降低了棄風、棄光成本。

③將碳排放成本加入DSO效益模型，能有效刺激TD內可再生能源出力，提升能源清潔性。

由于新型電力系統建設不斷完善，分布式可再生能源在配網側的接入比將不斷提升，未來將進一步研究配電側高比例可再生能源接入下的電碳協同市場機制優化問題，并針對各類可再生能源進行精細化建模，以確保系統安全高效運行。