基于KM 算法的轉發式干擾辨識與抑制方法

季 權，王 松，杜思予，陳望杰，劉泳伶

（1.中國航天科工集團8511研究所， 江蘇 南京 210007；2.中國人民解放軍32086部隊， 江蘇 南京 210018）

0 引言

在現代復雜電磁環境中，干擾裝備向綜合化、分布化、靈巧化方向發展，新型干擾技術層出不窮。特別是隨著數字射頻存儲（DRFM）技術的快速發展，基于DRFM 的干擾機能夠對截獲到的雷達信號進行分選、識別、存儲，然后快速調制轉發，產生大量相干干擾信號。此類干擾能夠在雷達信號處理階段獲得匹配濾波增益，形成大量能量較大的假目標，嚴重影響雷達的目標檢測與跟蹤能力。

目前，國內外學者從重構對消和干擾辨識2 個方向出發，提出了許多行之有效的抗干擾方法。在重構對消方面，文獻［1］基于自適應濾波估計干擾參數，重構出干擾信號，與原始回波對消；文獻［2］從脈壓數據中提取干擾參數重建干擾信號，進而實現干擾自適應對消。但是重構對消的思想對參數估計精度要求較高，若參數估計不準確，則干擾抑制效果不佳，也可能造成對消后目標信號的丟失。在干擾辨識方面，主要是利用目標和干擾在時域、頻域、空域、時-頻域、變換域等方面的特征差異進行信號識別、分類，從而抑制干擾信號。文獻［3—4］設計了一種空-時相位編碼信號，增強干擾與目標空-時分布差異，進而通過失配濾波器實現了干擾抑制；文獻［5］利用快-慢時間聯合域處理抑制干擾，但僅適用于非相干干擾；文獻［6—8］分別對回波信號進行Hough 變換和分數階傅里葉變換，根據變換域特征區分干擾和目標；文獻［9—10］通過分析干擾和目標在脈壓域的分布特征，檢測目標所在距離單元并剔除干擾，但干擾功率較大時算法失效；轉發式干擾的多普勒頻率通常集中分布于有限個鄰域內，文獻［11］利用這一點區分干擾和目標；文獻［12］設計頻率、極化聯合捷變波形，在接收端采用盲源分離算法抑制干擾。但此類方法無法適用單極化雷達，具有一定的局限性。

本文聚焦雷達對抗此類相干干擾的需求，首先對轉發式干擾的產生機理和干擾特性進行了詳細的分析，然后探討了捷變頻雷達波形抗此類干擾的能力，并結合頻率捷變技術帶來的主動對抗優勢，提出了一種基于K 均值（KM）聚類思想的干擾抑制方法。

1 信號模型

1.1 轉發式干擾

轉發式干擾一般是指干擾機對所截獲的雷達信號直接或進行幅度、相位、頻率、時延等調制后發射出去的干擾。此類干擾信號和雷達信號具有一定相參性，能夠獲得雷達接收機的匹配濾波增益，從而在距離維產生與真實目標相似，但能量更強的若干個虛假目標，達到迷惑、欺騙雷達的目的，同時具有壓制真實目標的干擾效果。

由于天線隔離度限制，實際應用中干擾設備多采用收發分時體制。干擾機對雷達發射信號進行采樣預存儲之后，經過延時直接轉發或多次延時后疊加轉發，可以形成單個或多個假目標干擾。通過調整采樣時長和轉發延時的時序關系，理論上能夠在匹配濾波輸出中實現任意密集度的假目標干擾效果。具體產生原理如圖1 所示。

圖1 轉發式干擾產生機理

假設干擾機截獲了第n個雷達發射脈沖st(t，n)，延時K次，將產生的K個時延信號在時域進行疊加轉發。因此，轉發式干擾信號sj(t，n)可以表示為：

式中，Δτk，n表示干擾機產生的第k個干擾信號相對于第n個雷達發射脈沖的延時；Aj(k，n)表示第n個脈沖對應的第k個時延干擾信號幅值。干擾機工作帶寬為[fj1，fj2]。

1.2 捷變頻雷達信號

頻率捷變是一種常用的干擾對抗手段。捷變頻雷達是指雷達相鄰發射脈沖間的載頻隨機或偽隨機跳變，干擾機難以準確預測出下一個脈沖的頻率，從而能夠有效對抗大功率噪聲壓制干擾和大部分欺騙干擾。典型的捷變頻雷達發射信號如圖2 所示。圖2中，f0表示初始載頻，Δf表示跳頻間隔。

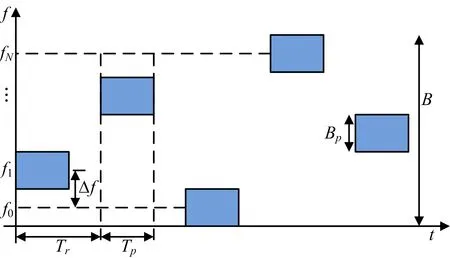
圖2 典型捷變頻雷達發射信號

假設雷達在一個相參處理間隔（CPI）內共發射N個脈沖信號，則第n個脈沖信號st(t，n)對應的載頻可以表示為：

式中，c(n)表示跳頻編碼，M表示跳頻點數，且有M≥N。那么，捷變頻雷達發射信號總帶寬B=M?Δf，第n個脈沖信號st(t，n)表示為：

式中，t為快時間，u(t)為發射信號基帶波形，采用線性調頻（LFM）信號時，u(t)=rect(t/Tp)exp(jπκt2)，κ=BP/TP表示線性調頻斜率，Bp和Tp分別表示發射脈沖帶寬和時寬，Tr表示脈沖重復周期。

以單個點目標為例，對于一個初始徑向距離r0，速度v0，做勻速直線運動的剛體目標，捷變頻雷達第n個脈沖的目標回波信號r(t，n)可以表示為：

式中，γ表示目標后向散射系數，τn=2(r0-v0(n-1)Tr)/c表示目標回波相對于發射脈沖的時延，c為光速。

2 抗干擾機理分析

干擾機利用截獲的雷達發射信號產生與真實回波高度相關的轉發式干擾，將會嚴重影響雷達的檢測跟蹤性能。轉發式干擾效果如圖3 所示，圖3（a）和（b）分別顯示了轉發式干擾對LFM 信號和捷變頻雷達信號的干擾效果。

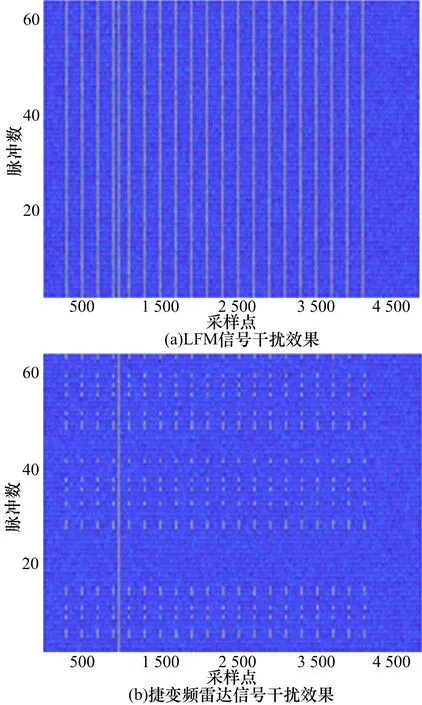
圖3 轉發式干擾效果

可以看到，對于LFM 雷達而言，疊加的干擾信號均獲得匹配濾波增益，使得真實目標淹沒在密集的逼真假目標中，難以有效區分；對于捷變頻雷達而言，由于干擾機收發分時，采樣到第n個發射信號無法與后續第n+1，n+2，…，N-q個脈沖匹配，其中，q為不大于N的任意正整數。因此，捷變頻雷達的回波信號中只有部分脈沖會受到干擾影響，這為后續的干擾辨識和干擾抑制處理提供了極大的便利。

由此，捷變頻雷達接收機接收到的第n個脈沖的回波信號sr(t，n)可以表示為：

式中，n(t)表示隨機高斯白噪聲。進一步地，對接收到的回波進行混頻和脈沖壓縮處理，得到的輸出為：

式中，復包絡u(t)為LFM 信號，A表示真實目標回波經過脈沖壓縮處理后的幅值，A′j(k，n)表示第k個假目標經過脈沖壓縮處理后的幅值；n′(t)表示脈沖壓縮處理之后的噪聲信號。

綜上所述，采用捷變頻波形降低了干擾在頻域的覆蓋率，從發射端提升了雷達的低截獲性能和抗干擾能力。

3 基于K-Means 聚類算法的干擾識別與抑制

KM 聚類算法是一種動態聚類算法，其主要思想是對N個待分選對象給出K（K≤N）個類劃分，將特征集中在任意k類的待分選對象進行分類組織。KM 算法以誤差平方和作為聚類準則，具有占有存儲空間小、算法簡單方便、聚類效率高等優勢，廣泛應用于雷達偵查領域，實現雷達輻射源信號分選與分類識別。雷達抗干擾技術也可以認為是一種信號分類識別的過程。因此，利用目標和干擾在脈壓域的分布特征差異，本文基于KM算法實現干擾識別與抑制處理，具體過程如圖4所示。

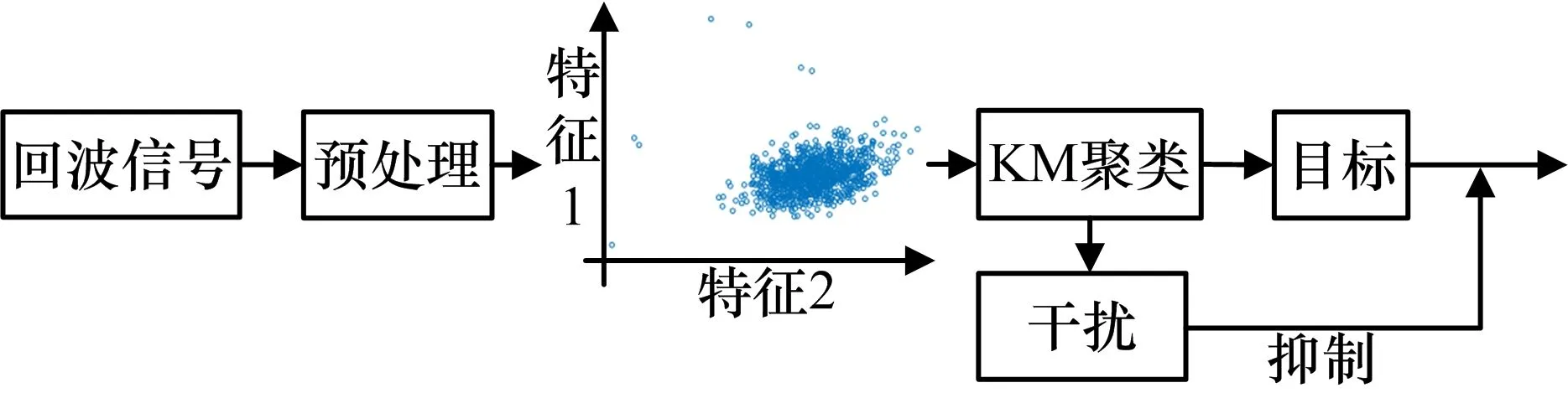
圖4 基于KM 算法的干擾識別與抑制流程

3.1 數據預處理

式（5）和式（6）的推導結果表明，經過脈沖壓縮處理之后，捷變頻雷達的目標回波是一條連續的直線，而轉發式干擾信號由于頻率失配而呈現出一定程度的離散化，參照圖3（b）。對于脈壓數據矩陣中的每個元素，分別沿距離維和速度維計算離散度。具體定義為：

式中，n，l分別表示速度單元索引和距離單元索引，An，l表示第n個脈沖、第l個距離單元對應的幅值；ω表示當前單元的鄰域長度。dr(l)表示第l個距離單元內脈壓數據的距離維離散度，dv(l)表示第l個距離單元內脈壓數據的速度維離散度。將dr(l)，dv(l)構成數據集DL×L={dr(l)，dv(l)}， 1 ≤l≤L。

3.2 干擾辨識與抑制

本文利用KM 聚類算法對回波數據進行識別、分類，進而實現干擾抑制。具體步驟如下：

步驟1：按照3.1 節對回波脈壓數據進行預處理，得到待分類數據集D={d1，d2，…，dL}，且dl=(dr(l)，dv(l))；

步驟2：初始化簇劃分Ck=?，k=1，2，…，K，從數據集D中隨機選擇K個樣本作為初始聚類中心μk∈{μ1，μ2，…，μK}；

步驟3：針對數據集中每個樣本dl，計算其到K個聚類中心的距離Δk=，并將其劃分到距離最小的聚類中心所對應的類λk中，此時Δλk=min {Δ1，Δ2，…，ΔK}，并更新簇Cλk=Cλk∪{dl}；

步驟4：針對每個類別對應的簇Ck中所有的樣本點重新計算聚類中心μk=1/ |Ck|（即屬于該類的所有樣本的質心）；

步驟5：重復步驟3—步驟4，直至聚類中心位置不再改變，聚類結果對應的損失函數最小，算法達到收斂。其中，損失函數定義為各個樣本距離所屬簇中心的誤差平方和：

式中，dl表示第l個樣本，Cl是dl所屬的簇，μCl表示簇Cl對應的聚類中心，L為樣本總數。

4 仿真實驗

本節通過仿真實驗驗證所提抗干擾算法的有效性和干擾抑制性能。仿真參數如表1 所示。

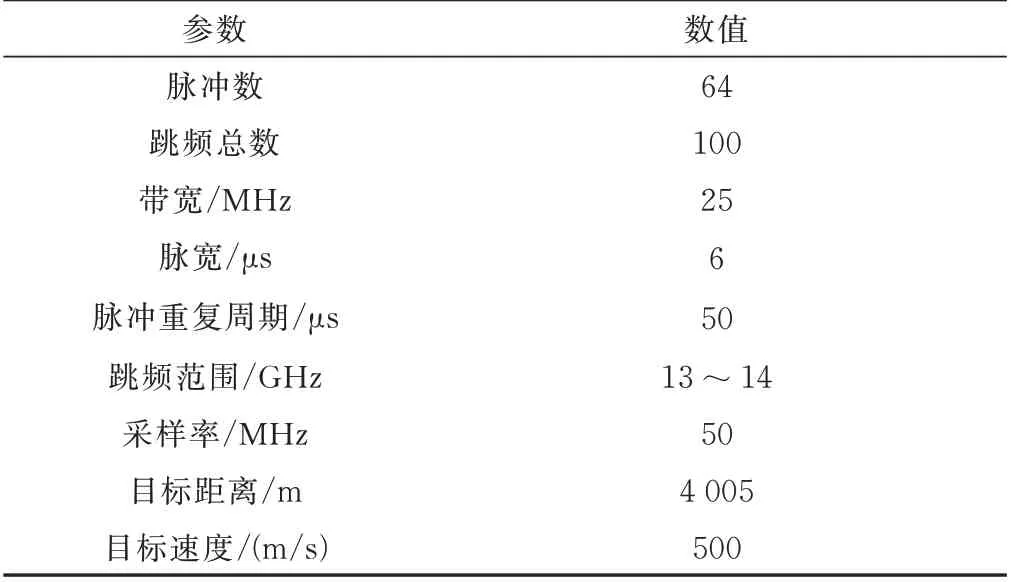
表1 仿真參數設置

干擾抑制過程仿真實驗結果如圖5 所示。其中，圖5（a）為捷變頻雷達回波的脈沖壓縮后結果，圖5（b）為圖5（a）的俯視圖。可以看出，干擾機對截獲到雷達發射脈沖信號進行多次轉發，經過脈壓處理之后，在距離向上形成功率較大的若干個假目標，覆蓋真實目標。但是由于干擾帶寬遠小于雷達跳頻帶寬，因此只有部分脈沖受到干擾機影響。進一步使用KM 算法對散點圖進行聚類，得到圖5（c）所示的聚類結果。根據聚類結果，濾除干擾信號，所得結果如圖5（d）所示。對比圖5（a）可以看到，脈壓距離單元內的假目標被抑制，只剩下目標信息，證明了所提算法抗轉發式干擾的有效性。

5 結束語

本文聯合捷變頻雷達“主動”對抗優勢，提出了基于KM 算法的抗轉發式干擾方案。與現有算法相比，論文所提方法具有以下優勢：不依賴于干擾和目標的多域特征差異，適用范圍更廣；算法邏輯和模型較簡單，具有一定的工程實際意義。■