湍流普朗特數在高超聲速繞流中的修正

劉景源

(南昌航空大學飛行器工程學院，江西 南昌 330063)

0 引言

高超聲速戰略、戰術飛行器設計是世界各航天航空大國所瞄準的一個重點研究方向[1-2]。為了提高高超聲速導彈、動能打擊等武器的機動性,舵面偏角會在較大范圍內發生變化,因此準確預估舵面偏角的氣動力、氣動熱對高超聲速武器系統的研制具有重要意義[3]。

應用基于雷諾平均的渦粘湍流模型仍然是高超聲速飛行器壓縮拐角類繞流的氣動力、氣動熱預估的設計工具。湍流熱通量的建模精度是制約氣動熱準確預估的一個重要因素[4-5]。

對湍流熱通量的建模有零方程、一方程、二方程模型,以及直接建立湍流熱湍流的微分方程模型等4種類型。零方程模型相比其余3種模型,因為無需建立微分方程,具有建模簡單、計算效率高、魯棒性強等優點,在高超聲速武器的氣動特性預估中得到了廣泛的應用[6-7]。由于零方程的梯度模型是基于雷諾比擬的假設建立的,比擬系數為湍流普朗特數,并且假設湍流普朗特數是常數,對高超聲速激波/湍流邊界層干擾導致的復雜流動的精確模擬存在缺陷[8-9]。文獻[10]提出計及湍流渦粘性與分子粘性系數比的變湍流普朗特數模型,但是該模型僅僅對不可壓縮流動進行的。文獻[6,11]發展了一種湍流普朗特數代數模型,高超聲速尖錐、雙楔、HIFiRE-1等外形的氣動熱計算結果表明,與湍流普朗特數為常數的數值結果相比,所發展的模型給出的表面熱流更精確。而文獻[4,5,9]提出的零方程湍流熱通量模型,均基于計及激波非定常效應,并在修正了的k-ω模型基礎上進行的。由于該k-ω模型眾所周知的缺陷,所提出的湍流熱通量模型聯合其他渦粘及雷諾應力模型的模擬精度需要進一步評估。

對高超聲速激波/湍流邊界層干擾導致的非平衡流動,湍流熱通量建模中的湍流普朗特數并非常數,而應為非平衡流動特征參數的函數,從而提出了一種修正的湍流普朗特數熱通量模型。應用數值模擬及理論分析方法,對高超聲速平板、壓縮拐角(高超聲速飛行器舵面的簡化外形)等繞流的數值分析,評估了所提出的零方程湍流熱通量模型。

1 控制方程及數值方法

基于RANS方程組及二方程SSTk-ω湍流模型方程組[12]進行零方程湍流熱通量模型修正及數值分析。數值模擬中,RANS及SSTk-ω方程組的對流項采用具有低耗散特性的經熵修正的二階TVD格式,RANS的黏性項,及SSTk-ω方程組的擴散項,湍動能生成項等均采用二階中心差分格式進行離散。湍流方程組的負源項則采用點隱格式以提高計算效率。具體的數值方法、邊界條件,以及對數值方法的驗證等見文獻[13,14]。

2 湍流普朗特數的修正方法

文獻[4-9]均表明湍流普朗特數為常數的零方程湍流熱通量模型,在模擬高超聲速飛行器激波/湍流邊界層干擾等強非平衡湍流繞流的表面熱流存在缺陷,因此需要發展計及高超聲速非平衡流動特性的變湍流普朗特數模型。基于衡量高超聲速非平衡特性的參數——湍動能生成與湍流耗散率比值的無量綱數,提出一種湍流普朗特數修正模型如下:

(1)

式中:Pk為湍動能生成項;ε為湍動能耗散率[15]。

對于SSTk-ω模型,湍動能耗散率ε可表示為:

ε=cμρωk+δ

(2)

其中δ是為避免式(1)中的分母為零而出現的小量,取δ=1×10-30。

文獻[15]采用限制器,對湍動能生成與湍流耗散率比值的大小進行限制,避免湍動能生成項的非物理增長。式(1)亦采用上述方法對湍流普朗特數的大小進行限制。由文中分析結果可見,所采用的限制方法能夠提高湍流模型預測精度。

由式(1)可見,當非平衡無量綱參數(湍動能生成與湍流耗散率比值)的比值小于1.2時,即為湍流原湍流普朗特常數0.9;而當非平衡參數大于1.2時,湍流普朗特數變小,極小值為0.2。湍流普朗特數的極小值取值對高超聲速激波/湍流邊界層干擾導致的局部高熱流具有重要的影響,文獻[16]基于提出的二方程湍流熱通量模型,計算的高超聲速激波/湍流邊界層干擾流動的表面熱流結果表明,湍流普朗特數最小可取0.2,因此基于文獻[16],文中給出的最小湍流普朗特數為0.2。

3 算例驗證

為了驗證所提出的湍流熱通量的普朗特數修正方法,下面給出了高超聲速平板以及15°,30°,34°壓縮拐角等4個算例的驗證結果。其中網格、數值方法、邊界條件及驗證等見文獻[13,14]。

3.1 高超聲速平板繞流

選取文獻[17]給出的高超聲速平板繞流的實驗測量結果,進行修正湍流普朗特數模型的驗證。實驗的來流馬赫數為8.18,來流溫度81 K,基于來流條件的每米雷諾數為4.9×106m-1,平板壁面溫度為300 K。

圖1給出了原SSTk-ω湍流模型、在原SSTk-ω湍流模型基礎上分別進行湍流普朗特修正的Kays模型[10]、文中提出的式(1)模型,計算高超聲速平板速度型,并與實驗數據的對比結果。

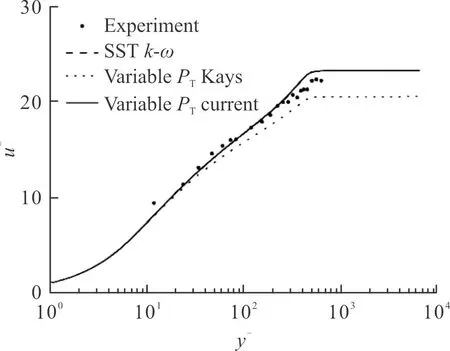
圖1 高超聲速平板速度型(x=1.80 m,Ma=8.18)Fig.1 Computed velocity profile for a Mach 8.18 flat plate at x=1.80 m

由圖1可見,文中的修正模型與湍流普朗特數為常數的模型計算結果相同。原因為文中修正模型對高超聲速平板湍流平衡繞流,式(1)等號右端第二項設計的函數項不起作用,即對高超聲速平衡繞流流動,文中的修正模型,退化為原模型的普朗特數。而對于Kays模型,由于該模型是基于不可壓縮流動提出的,對高超聲速可壓縮平板流動,計算結果與實驗數據相比有一定差距,該模型還需要進一步研究改進。

圖2給出了原SSTk-ω湍流模型、在原SSTk-ω湍流模型基礎上分別進行湍流普朗特修正的Kays模型[10]、文中提出的式(1)模型,計算的高超聲速平板壁面熱流并與實驗數據的對比曲線。由圖2可見,文中的修正模型與湍流普朗特數為常數的模型計算結果相同,其原因與對圖1的分析相同。Kays模型計算的平板壁面熱流雖然也與實驗結果符合較好,但比其他模型稍高。原因為Kays模型計算給出的Kármár常數κ較大,由文獻[14]的分析,則摩擦系數cf增大。再由摩擦系數與壁面熱流的雷諾比擬理論,則Kays模型計算的壁面熱流比其他兩個模型稍大。

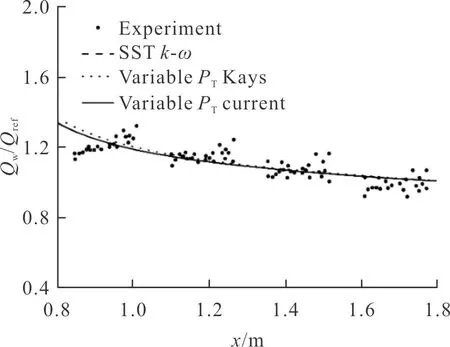
圖2 高超聲速平板壁面熱流Fig.2 Wall heat flux over the flat plate

3.2 高超聲速15°壓縮拐角繞流

下面選擇文獻[18]的實驗條件為計算條件高超聲速15°壓縮拐角繞流進行算例驗證。算例的來流馬赫數及來流溫度分別為9.22 K、64.5 K,基于來流參數的每米雷諾數為4.7×107m-1,壁面溫度為295 K。

圖3(a)與圖3(b)分別給出了原SSTk-ω湍流模型、在原SSTk-ω湍流模型基礎上分別進行湍流普朗特修正的Kays模型[10]、文中提出的式(1)模型,計算的高超聲速15°壓縮拐角壁面壓強、壁面熱流并與實驗數據的對比曲線。由圖3可見,對高超聲速15°壓縮拐角繞流,由于拐角角度較小,對湍流流動,由激波/湍流邊界層干擾導致逆壓梯度并未使流動分離,流動的非平衡性較弱,對式(1)中湍流普朗特數的影響較小,因此,修正模型與原模型及Kays模型計算給出的壁面壓強和壁面熱流均符合較好。各模型給出的壁面壓強均與實驗數據有一定差別,可能是實驗有一定誤差,需要進一步研究。修正模型計算的表面熱流與實驗結果更接近,最大熱流相對誤差小于5%。

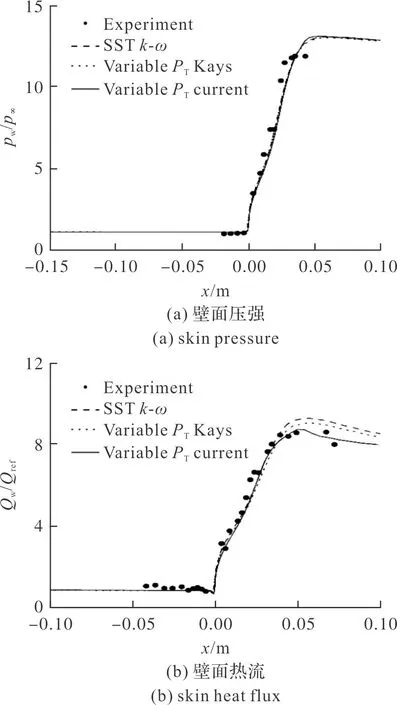
圖3 Ma=9.22,15°壓縮拐角壁面壓強、熱流Fig.3 Skin pressure and the skin heat flux distributions for free stream Mach 9.22 flow into a 15° compression corner

3.3 高超聲速30°壓縮拐角繞流

下面選擇30°壓縮拐角進行算例驗證,其余所有條件均與算例3.2節相同。

圖4(a)與圖4(b)分別給出了原SSTk-ω湍流模型、在原SSTk-ω湍流模型基礎上分別進行湍流普朗特修正的Kays模型[10]、文中提出的式(1)模型,計算的高超聲速30°壓縮拐角壁面壓強、壁面熱流,及與實驗數據的對比曲線。由圖4(a)可見,由于原SSTk-ω湍流模型與Kays模型并未準確計及高超聲速激波/湍流邊界層流動的湍流普朗特數,導致數值模擬結果出現了流動分離及再附,以及由于流動分離導致了原SSTk-ω湍流模型與Kays模型,在拐角附近區域出現分離泡(見圖5(a)),在再附區出現了壓強極值,及壓強極值后的平臺效應,從而使計算的壁面壓強與實驗數據相差較大。由于原SSTk-ω湍流模型與Kays模型模擬給出了流動分離及再附,但實驗結果表面,流動基本上并未分離,因此導致圖4(b)中原SSTk-ω湍流模型與Kays模型計算的拐角附近區域的熱流較大,并且再附區的熱流遠高于實驗數據。文中提出的修正模型,即式(1),由于正確預測了流動基本無分離(見圖5(b))則給出了與實驗符合良好的壁面熱流結果,最大熱流相對誤差小于5%。

圖4 Ma=9.22,30°壓縮拐角壁面壓強、熱流Fig.4 Skin pressure and the skin heat flux distributions for free stream Mach 9.22 flow into a 30° compression corner

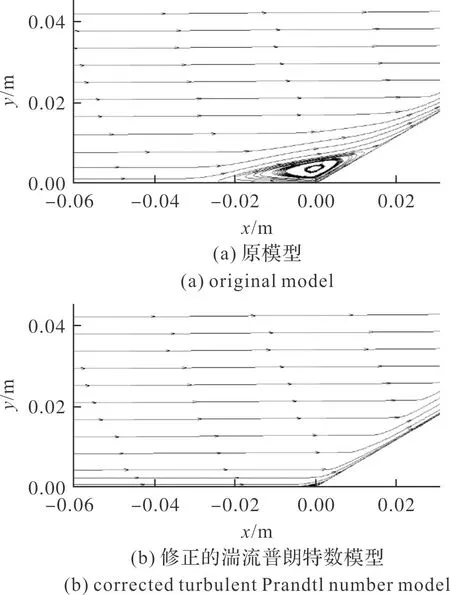
圖5 Ma=9.22,30°壓縮拐角流線分布Fig.5 Streamline distributions for 30° compression corner at free stream Mach 9.22

3.4 高超聲速34°壓縮拐角繞流

下面選擇34°壓縮拐角進行算例驗證,其余所有條件均與算例3.2節、3.3節相同。

圖6(a)與圖6(b)分別給出了原SSTk-ω湍流模型、在原SSTk-ω湍流模型基礎上分別進行湍流普朗特修正的Kays模型[10]、文中提出的式(1)模型,計算的高超聲速34°壓縮拐角壁面壓強、壁面熱流,及與實驗數據的對比曲線。由圖6(a)可見,雖然原SSTk-ω湍流模型與Kays模型均在壓縮拐角附近計算出了流動分離及再附,但由于原SSTk-ω湍流模型與Kays模型并未準確計及高超聲速激波/湍流邊界層時的湍流普朗特數,與實驗結果相比,預測的分離區偏大(如圖7(a)所示)、峰值壓強及再附區后移。文中的修正模型則較好地預測了流動分離及再附(如圖7(b)所示),因此給出與實驗數據符合較好結果。由于原SSTk-ω湍流模型與Kays模型預測的分離及再附區較大,由圖6(b)可見,所計算的峰值熱流位置及大小均與實驗結果有一定差別,而文中提出的修正模型的計算結果與實驗數據符合較好,最大熱流相對誤差小于6%。

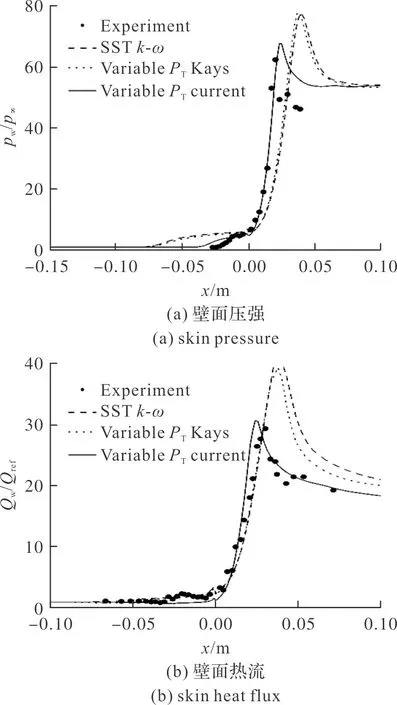
圖6 Ma=9.22,34°壓縮拐角壁面壓強、熱流Fig.6 Skin pressure and the skin heat flux distributions for Mach 9.22 flow into a 34° compression corner

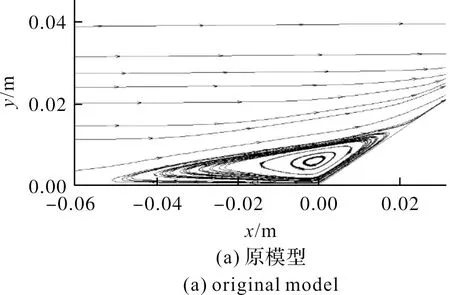
圖7 Ma=9.22,34°壓縮拐角流線分布Fig.7 Streamline distributions for 34° compression corner at free stream Mach 9.22

4 結論

應用數值模擬及理論分析方法,針對高超聲速壓縮拐角激波/湍流邊界層干擾導致的復雜流動,提出了一種湍流熱通量建模中的湍流普朗特數并非常數,而應為非平衡流動特征參數的函數的湍流普朗特數模型,并與實驗結果、原湍流普朗特數模型、Kays湍流普朗特數模型的計算結果進行對比,主要結論如下:

1)對高超聲速平板的平衡湍流流動建立的模型不改變湍流普朗特數,修正模型與原模型計算精度相同。

2)對高超聲速激波/湍流邊界層干擾導致的復雜非平衡流動,湍流普朗特數并非常數,應進行修正。

3)應用所提出的湍流普朗特數為非平衡流動特征參數的函數的湍流熱通量模型,數值模擬與實驗結果的對比表明,該模型計算氣動力、氣動熱更精確。

雖然文中所提出的模型,在計算高超聲速壓縮拐角繞流中取得了較好的結果,但是由于高超聲速激波/湍流邊界層干擾的復雜性,進一步應研究所提出的修正湍流普朗特數模型對復雜流動的模擬能力。