一類含有有色噪聲的魯棒非線性擴展狀態估計*

師衛國，朱可欣，董燕飛，祁 林，賀 偉，侯 寧

（河南城建學院電氣與控制工程學院，河南 平頂山 467036）

0 引言

狀態估計問題作為控制和信號處理領域的基礎研究課題之一，在過去幾十年中被學者們廣泛研究。狀態估計的主要思想是根據系統模型和測量輸出信號對給定系統的內部狀態進行估計，從而實現準確預測和控制系統。到目前為止，狀態估計器已在飛機跟蹤、智能電網和生物過程監控等領域成功應用［1-3］。隨著科技的進步，對于狀態估計方法和系統噪聲約束的研究取得了新的進展，H∞估計、分布式狀態估計、滾動時域估計和噪聲處理等方案已得到廣泛研究，并應用于工程實驗［4-7］。

近年來，非線性系統因其在理論分析和實際應用中的重要性引起人們的廣泛關注。在大多數應用中，非線性變量的存在使得系統性能難以得到精確的分析和控制，如果處理不當，可能會降低系統性能，甚至導致不穩定［8-9］。對非線性系統的狀態估計，已經進行了許多方案研究，例如自適應控制、擴展卡爾曼濾波和粒子濾波［10-12］。文獻［13］針對一類具有全狀態約束和未知時滯的非線性隨機系統，提出了一種自適應神經網絡控制器。將系統轉化為非線性映射的約束自由系統，補償未知時滯不確定性，利用神經網絡逼近設計過程中出現的未知非線性函數，該方法能夠實現閉環系統信號的最終有界性和全狀態約束。擴展狀態觀測器是一類用于不確定非線性系統輸出反饋控制的高增益觀測器，本文提出了一種新的級聯設計，將飽和度轉變為內部變量，以限制最大實現增益，相比標準觀測器的輸出，反饋控制具有更強的不確定性估計、補償能力和收斂性［14］。文獻［15］針對一些強的非線性系統，通過將非線性函數擴展成為系統狀態，設置函數變化率上界，降低非線性干擾對系統的影響，該方法在估計性能方面具有很好的效果。

網絡化系統通過共享的通信通道將系統和控制器連接起來，可以輕松構成新的體系結構，同時具有成本優勢，因而被廣泛應用于交通、醫療、電力系統等領域［16-18］。然而，當大量系統同時共享一個公共通信通道時，網絡系統中的通信容量限制是不可避免的。為了克服這一問題，在過去幾十年中，研究人員對傳輸調度問題做了許多工作，為網絡系統設計了不同種類的傳輸調度協議。文獻［19］研究了在網絡中節點間通信帶寬有限，在節點間交換的信息必須量化的情況下，求解分布式凸優化問題的梯度方法。提出了一種改進的基于共識的梯度方法來解決這類問題，研究了系統的收斂性，并給出了收斂速度。文獻［20］采用輪詢協議周期性地發送測量數據，克服了通信容量的限制。由于調度協議改變了測量結構，導致循環調度誘導的周期性擴展狀態系統不可觀測，本文建立了周期擴展狀態系統的可觀測性充要條件。文獻［21］設計了一種動態事件觸發器，使控制器只在觸發時刻解決優化問題，觸發閾值與反饋策略的插值系數相關，并通過優化確定。利用插值技術構造反饋策略，對原系統約束進行緊化，滿足魯棒約束。

基于上述說明，本文主要研究約束信道下的非線性不確定系統的狀態估計問題，貢獻如下：

1）創新測量信息逐差法處理有色噪聲的相關性問題，解決標準卡爾曼濾波無法處理相關噪聲的難題；

2）通過使用對數量化器降低通信網絡的傳輸壓力，利用矩陣不等式消除量化誤差，保證系統的魯棒性；

3）將非線性項作為系統狀態，構造擴展狀態系統，設計擴展狀態估計器。通過Young’s 不等式求解先驗估計誤差協方差上界和估計誤差協方差上界，在此基礎上優化估計器增益。此方法處理非線性更加簡單，針對強非線性系統仍然具有良好的估計效果。

1 問題描述

1.1 系統模型

文中，考慮如下的非線性時變系統：

1.2 有色噪聲

有色噪聲vk滿足下列條件：

假設1 噪聲ωk和uk為互不相關的白噪聲，滿足：

其中，δkj為Kronecker 函數：

1.3 非線性擾動

1.4 量化測量

為了降低通信通道的傳輸壓力，本文采用對數量化器對測量信息進行處理，對數量化器的量化集合為：

其中，0＜ρj＜1 為量化密度，u0為初始向量，n 為量化級數。

同時，測量方程滿足的下列映射關系：

根據對數量化器的定義，測量信息可以表示為：

引理3 給定實數矩陣B，X，等式滿足下列特點［24］：

2 魯棒擴展狀態估計器設計

在進行魯棒擴展狀態估計器設計之前，先對系統作出下列假設：

假設4 非線性函數的變化率gi（xk）滿足：

根據卡爾曼濾波的定義，結合系統測量方程，分別給出先驗估計值、后驗估計值、先驗估計誤差協方差和后驗估計誤差協方差的定義：

結合定義和系統的測量信息，魯棒擴展狀態估計器可以設計為：

其中，Kk+1表示狀態估計器增益。

以上工作內容為接下來魯棒擴展狀態估計器設計做了很好的鋪墊，在估計器設計過程中，計算增益矩陣Kk和誤差協方差上界是非常重要的環節，接下來的主要任務便是通過分析和計算估計誤差協方差，得到這些參數，完成狀態估計器設計。

其中，

Step 1 解決式（19）中的交叉項，采用引理1，得到下列不等式：

然后，將式（24）和式（25）的結果代入式（19），下列等式成立：

Step 2 首先利用引理1 解決式（20）中的交叉項，再采用引理2 處理量化誤差。

接下來，采用引理2 處理對數量化器造成的量化誤差：

將以上結果代入式（20），可以得到下列不等式：

其中，

其中，

至此，定理1 證明完畢。

定理2 利用定理1 計算的結果，計算增益矩陣Kk+1的更新方程為：

證明

至此，定理2 證明完畢。

3 仿真實驗

在本章中，通過仿真數例來驗證所設計的魯棒擴展狀態估計方案的有效性。

3.1 系統說明

案例選取的非線性函數如下：

系統矩陣選取：

估計器參數選取：

3.2 仿真方案

接下來，將通過6 個仿真方案，對設計的估計器性能進行對比分析，充分論證魯棒非線性時變擴展狀態估計算法的合理性和有效性。

方案1：根據非線性時不變系統，設計魯棒非線性狀態估計器，系統參數選取如下：

方案2：根據非線性時變系統，利用對數量化器處理測量信息，設計魯棒非線性擴展狀態估計算法，量化密度為ρ=0.5，初始向量u0=100。

然后利用控制變量法，對比魯棒非線性擴展狀態估計器性能，具體方案如下：

方案3：量化密度為ρ=0.3，初始向量u0=100；

方案4：量化密度為ρ=0.9，初始向量u0=100。

方案5：量化密度為ρ=0.5，初始向量u0=100；

方案6：量化密度為ρ=0.5，初始向量u0=10。

為了驗證本次估計算法對非線性系統的一定普適性，特給出方案7 進行說明，采用的非線性函數如下：

3.3 仿真效果

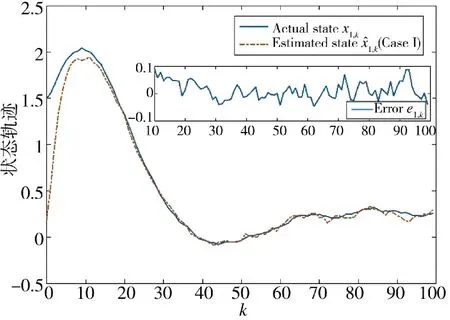
圖1 狀態x1，k 的實際值和估計值（方案1）Fig.1 Actual and estimated values of state x1，k（Scheme 1）

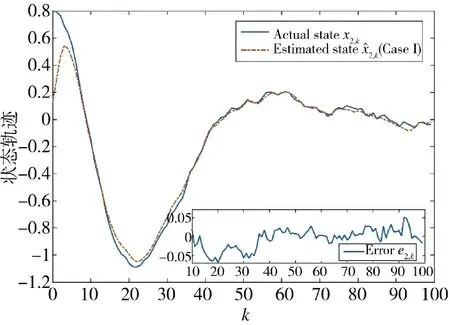
圖2 狀態x2，k 的實際值和估計值（方案1）Fig.2 Actual and estimated values of state x2，k（Scheme 1）

圖3 估計誤差協方差及其上界（方案1）Fig.3 Estimation error covariance and its upper bound（Scheme 1）

從圖4 ～圖7 可以看出，方案2 設計的估計算法具有良好的估計效果，由于是基于非線性時變系統進行設計，其工程價值明顯高于時不變系統。對比方案1，在估計誤差協方差方面，時變系統的波動性和數值均大于時不變系統，這是系統本身存在的差異，同樣表明了估計器設計的合理性。

圖4 狀態x1，k 的實際值和估計值（方案2）Fig.4 Actual and estimated values of state x1，k（Scheme 2）

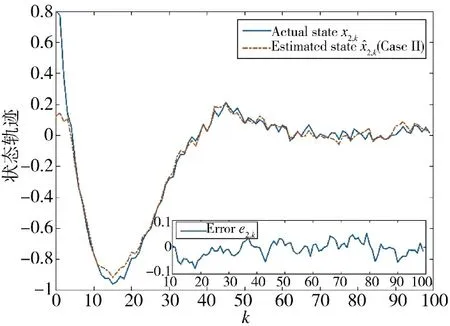
圖5 狀態x2，k 的實際值和估計值（方案2）Fig.5 Actual and estimated values of state x2，k（Scheme 2）

圖6 估計誤差協方差及其上界（方案2）Fig.6 Estimation error covariance and its upper bound（Scheme 2）

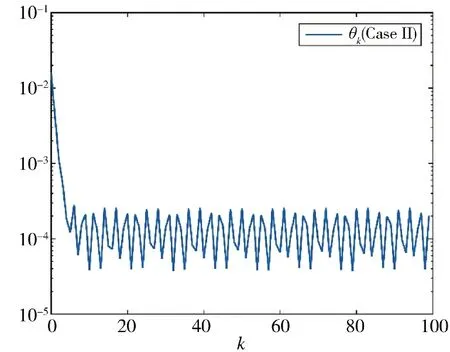
圖7 參數θk 的變化情況（方案2）Fig.7 Variation of parameter θk（Scheme 2）

從圖8～圖11 可以得到，在方案3 和方案4 的估計效果對比中，量化密度小的估計誤差大于量化密度大的估計誤差，充分說明量化密度對于系統性能的影響。從圖11 的估計誤差協方差可以清晰地看出，量化密度大的估計誤差協方差更小，性能更優。

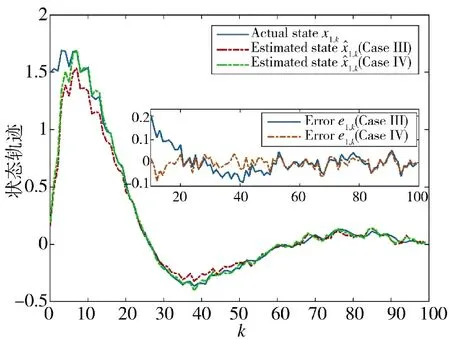
圖8 狀態x1，k 的實際值和估計值（方案3 和方案4）Fig.8 Actual and estimated values of state x1，k（Scheme 3 and Scheme 4）

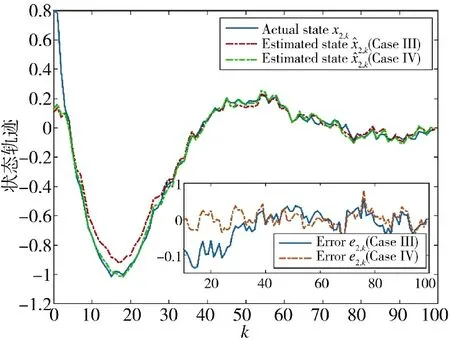
圖9 狀態x2，k 的實際值和估計值（方案3 和方案4）Fig.9 Actual and estimated values of state x2，k（Scheme 3 and Scheme 4）

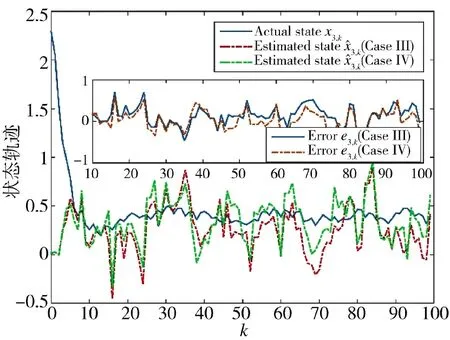
圖10 狀態x3，k 的實際值和估計值（方案3 和方案4）Fig.10 Actual and estimated values of state x3，k（Scheme 3 and Scheme 4）

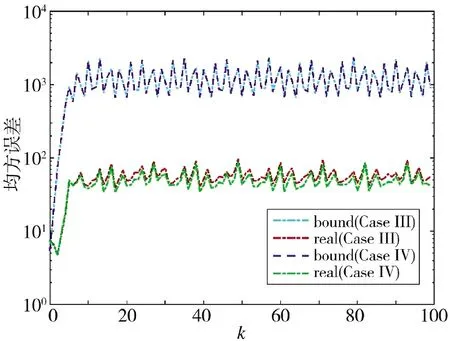
圖11 估計誤差協方差及其上界（方案3 和方案4）Fig.11 Estimation error covariance and its upper bound（Scheme 3 and Scheme 4）

通過圖12～圖15 的對比，可以看出初始向量對估計算法的影響不大。兩種方案中，方案5 的初始向量較大，在估計狀態、估計誤差和協方差方面的值還是小于方案6，說明初始向量可以影響性能，且相對較大性能更好。

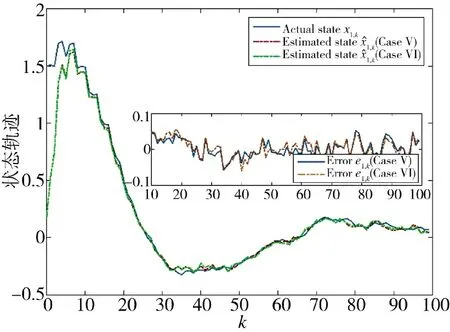
圖12 狀態x1，k 的實際值和估計值（方案5 和方案6）Fig.12 Actual and estimated values of state x1，k（Scheme 5 and Scheme 6）

圖13 狀態x2，k 的實際值和估計值（方案5 和方案6）Fig.13 Actual and estimated values of state x2，k（Scheme 5 and Scheme 6）

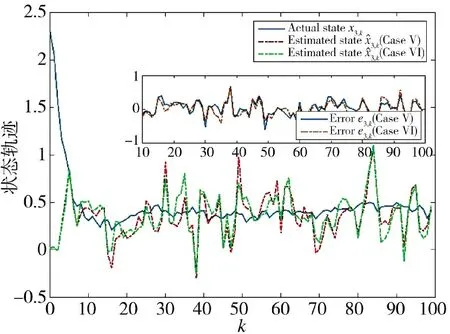
圖14 狀態x3，k 的實際值和估計值（方案5 和方案6）Fig.14 Actual and estimated values of state x3，k（Scheme 5 and Scheme 6）

圖15 估計誤差協方差及其上界（方案5 和方案6）Fig.15 Estimation error covariance and its upper bound（Scheme 5 and Scheme 6）

通過圖16～圖19 可以得到，算法針對不同的非線性系統同樣具有不錯的估計效果。系統的各個狀態均能夠被跟蹤，同時估計誤差協方差具有穩定上界，說明所設計的估計器具備一定普適性和合理性。

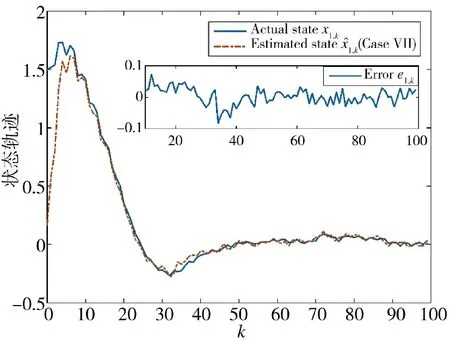
圖16 狀態x1，k 的實際值和估計值（方案7）Fig.16 Actual and estimated values of state x1，k（Scheme 7）

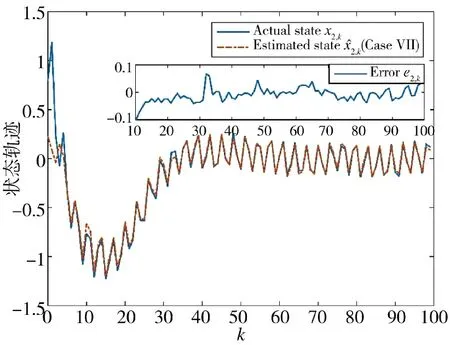
圖17 狀態x2，k 的實際值和估計值（方案7）Fig.17 Actual and estimated values of state x2，k（Scheme 7）

圖18 狀態x3，k 的實際值和估計值（方案7）Fig.18 Actual and estimated values of state x3，k（Scheme 7）

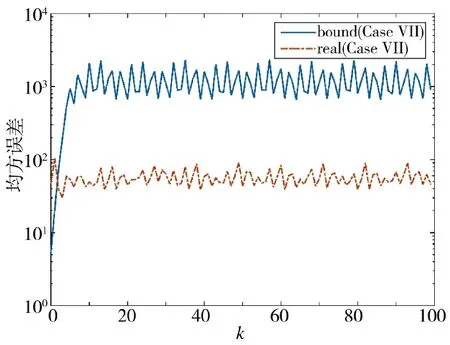
圖19 估計誤差協方差及其上界（方案7）Fig.19 Estimation error covariance and its upper bound（Scheme 7）

4 結論

在本文中，創新地使用擴展狀態方式處理系統非線性，設計了能夠處理有色噪聲和帶寬受限的魯棒擴展狀態估計算法。針對標準卡爾曼濾波無法處理有色噪聲的問題，總結出了測量信息逐差法；考慮到網絡化系統存在通信受限情況，采用對數量化器進行信息處理，提高網絡傳輸安全性；創新非線性系統分析方法，利用擴展狀態方式進行解決。擴展狀態卡爾曼濾波在處理強非線性方面具有很好的效果，同時運用非線性變化率的界作為約束條件，降低了非線性系統分析研究的保守性。算法給出了估計誤差協方差上界的計算方法，實現了增益的實時優化。通過仿真實例驗證了所研究算法的合理性、有效性和普適性。