加入淘汰機制的改進麻雀搜索算法*

周建新，侯宏瑤，鄭日成

（華北理工大學電氣工程學院，河北 唐山 063000）

0 引言

近幾年，參數優(yōu)化問題受到了廣泛的關注，而傳統(tǒng)的優(yōu)化方法（枚舉法、牛頓法、單純形法等）無法在短時間內求得最優(yōu)解或近優(yōu)解［1］。群智能算法（swa rm intelligence algorithm，SIA）的提出為傳統(tǒng)的控制方法提供了全新的思路，其在各學科中都逐漸展示出了強大的效果。尤其在控制工程領域，成為了一種對非線性、高緯度系統(tǒng)尋找最優(yōu)值的強有力手段。

SIA 是一種根據人為經驗或者自然規(guī)律所構造的數值尋優(yōu)方法，具有自組織、自學習、自適應能力，且能夠在可接受的計算花費下給出一個較優(yōu)的可行解［2］，對于求解不同類型的系統(tǒng)具有通用性。其主要原理是根據生物捕食、游走、遷徙等行為特征和自然法則，并依托計算機強大的數據處理能力來解決問題。基于其突出的優(yōu)點，SIA 得到了迅速發(fā)展，近期提出烏鴉搜索算法（CSA）、海鷗優(yōu)化算法（SOA）、灰狼算法（GWO）、鯨魚優(yōu)化算法（WOA）、蜻蜓算法（DA）等［3-7］。

麻雀搜索算法（SSA）由薛建凱于2020 年提出［8］，該算法較其他群智能優(yōu)化算法，優(yōu)點是原理比較簡單、易于實現、速度快、收斂精度高。但同其他SIA一樣都存在一些固有的問題，面對高緯度復雜函數模型尋優(yōu)時，種群初始化時位置隨機產生，所以迭代后期易出現多樣性不足，導致全局搜索能力有所下降；由于其機制問題，當緯度增加時無法更好地平衡局部與全局搜索能力。雖相比于其他基礎群智能算法，SSA 保持有較高的收斂速度，但仍有很大的改進空間。

針對這些在尋優(yōu)效果上出現的問題，相關學者和工程人員對SSA 進行了一些改進，改進側重點主要分為兩部分：一是在初始化種群參數方面，二是在種群搜索與收斂機制方面。例如，高晨峰等提出了一種黃金正余弦和曲線自適應的多策略麻雀搜索算法［9］，采用Chebyshev 混沌映射，改善了種群多樣性，并融合黃金正余弦算法，增加了發(fā)現者之間的信息交流，在更新公式中添加自適應權重改善了易陷入局部最優(yōu)的問題。李愛蓮等提出一種融合正余弦和柯西變異的麻雀搜索算法［10］，借助折射反向學習機制初始化種群，且在發(fā)現者、跟隨者位置更新公式上加入了正余弦算法和柯西變異擾動策略，提高了算法尋找全局最優(yōu)解的能力。尹德鑫等提出了一種多策略改進的麻雀搜索算法［11］，對步長因子動態(tài)調整，并在偵察預警麻雀的位置上引入了Levy 飛行，提高了算法整體的尋優(yōu)效果。

上述針對SSA 的改進策略通過加入初始化方法，提高了全局搜索能力；對收斂機制的改善，解決了傳統(tǒng)SSA 對于平衡全局搜索和局部收斂方面的缺點。但經實驗，其在面對高緯度復雜系統(tǒng)尋優(yōu)時，效果并不能完全滿足要求，在性能方面仍具有很大的改進裕度。針對此問題，本文提出了一種加入2N分段Tent 混沌映射和末位淘汰機制的改進麻雀搜索算法（TESSA）。

首先，在種群位置初始化時采用2N分段Tent混沌映射，使其初始位置更加具有均勻性和遍歷性，增加種群多樣性，提高算法收斂速度與全局搜索能力。其次，在種群位置更新后期加入淘汰機制，加快局部收斂速度與精度，同時改進跟隨者位置更新公式為一種非線性自適應擾動，更好地平衡了全局尋優(yōu)與局部挖掘能力，整體上進一步提升了SSA在數值尋優(yōu)方面的效果。

1 基本麻雀搜索算法（SSA）

SSA 是受麻雀種群的覓食與生存行為啟發(fā)而產生的一種數值尋優(yōu)算法。其種群中包含3 類個體，第1 類是適應度值較高的發(fā)現者，這些麻雀總會找到食物最為豐富的地點，并且會帶領整個種群進行覓食行為。第2 類為跟隨者，它們會監(jiān)視發(fā)現者的覓食行為并與之爭奪食物來提高自己的捕食率。第3 類為偵察者，當偵察者發(fā)現捕食者后立即發(fā)出報警信號，全體麻雀做出反捕食行為［12］。種群中每只麻雀的當前所在位置表示其對應解空間中的一個可行解。對于單只麻雀，有，其中，i表示當前麻雀編號。則種群中所有麻雀的位置可表示為：

其中，P 表示麻雀種群數量，d 為待求解問題維度；f（xP）表示每只麻雀所對應的適應度值，則麻雀種群所對應的適應度值為：

發(fā)現者的位置更新有兩種方式，其分別如式（3）所示：

跟隨者則會不斷監(jiān)視發(fā)現者的行為，一旦其發(fā)現了食物，跟隨者會立馬進行食物資源的爭搶，其位置更新公式如式（4）所示：

另外，種群中還存在10%～20%的警覺者，當其意識到危險時，會靠近其他麻雀來降低自己被捕食的幾率，其位置更新如式（5）所示：

其中，Xbest為全局最佳位置；β 為服從均值為0，方差為1 的正態(tài)分布隨機數；K∈［-1，1］為一個隨機數；ε 為極小常數，避免分母為0；fi為當前麻雀個體適應度值；fg與fw分別為當前全局最優(yōu)和最差適應度值；當fi＞fg時，表示當前個體處于種群邊緣，可能會受到捕食者的攻擊；fi= fg時，表明此時位于中心的麻雀感知到了危險，它們需要不斷靠近附近同伴，來減少自己被捕食的幾率。

2 加入淘汰機制的麻雀搜索算法

2.1 2N 分段Tent 混沌映射

傳統(tǒng)的SSA 隨機產生初始種群位置，容易導致后期種群多樣性降低，收斂速度變緩。而混沌映射有較好的均勻性與遍歷性，其被廣泛應用于各種算法當中。常見的有Sine 映射、Logistic 混沌映射、Circle 混沌映射等。

Tent 混沌映射具有對初值不敏感，分布均勻等特點。故本文采用以一種對其改進后的2N分段Tent混沌映射來對SSA 種群位置進行初始化［13］，提高種群多樣性。其表達式如式（6）所示：

其中，2N為分段數；Xn+1為經過映射后的數值；h 為設定的（0，1）之間常數；當2N=1，即N=0 時，式（6）即為普通的Tent 混沌映射。Lyaponuv 指數常常用來判斷系統(tǒng)的混沌性，其定義式為式（7）：

由式（7）計算出2NTent 混沌映射的Lyaponuv指數大于普通Tent 混沌映射。所以，2N越大，其對于SSA 種群位置的初始化則更具有隨機性和遍歷性。但同時隨著指數N 不斷增大，計算時間也會成倍增加，為了平衡種群多樣性與搜索時間，選取2N=16。

2.2 加入淘汰機制

傳統(tǒng)麻雀搜索算法中，種群會根據式（3）～式（5）不斷更新自己的位置，以達到逐步尋優(yōu)，但這種方式比較依賴與公式所定義的搜索范圍和步長，導致算法迭代速度不太穩(wěn)定。針對此問題，本文提出了一種在經過3 個公式的位置更新后，對此次迭代中所有個體加入淘汰機制來加強算法的收斂速度。

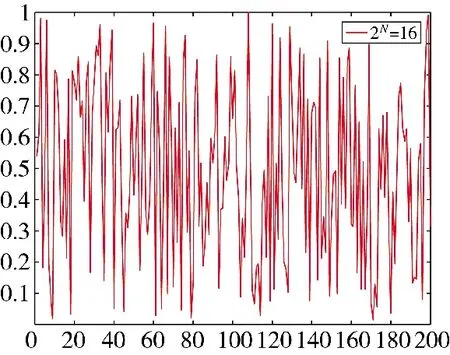
圖1 2N=16 時Tent 映射分布Fig.1 Distribution of Tent mapping when 2N=16

2.2.1 淘汰個體位置更新策略

淘汰機制即通過計算此次迭代中所有麻雀個體所對應的適應度值，淘汰掉適應度值排在末位的M 只個體，由于其被淘汰，所以下一代個體位置會更加傾向于在上代最優(yōu)值附近產生。新生成的個體位置按照式（8）進行更新：

2.2.2 自適應淘汰個體數量

由上述可知M 作為被淘汰個體的數量，其所設定的數值對平衡收斂速度與尋優(yōu)精度具有重要意義。分別取M=0.2，M=0.4，測試函數如表1 所示，取最大迭代次數為100，種群數量為50，發(fā)現者所占比例為20%，警覺者比例為10%，其尋優(yōu)效果如圖2所示。

表1 F1 測試函數Table 1 F1 test function

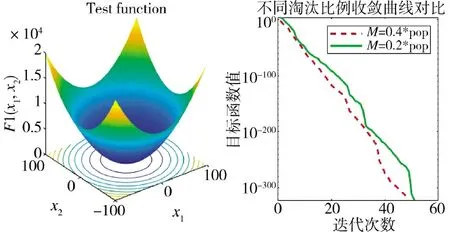
圖2 不同淘汰比例下的收斂曲線Fig.2 Convergence curves under different elimination ratios

由圖2 可知，雖然較大的M 會使算法收斂速度加快，但由于其不斷在最優(yōu)值附近產生固定的M 只新個體，容易導致全局搜索能力不足，迭代后期出現速度下降、無法收斂至極小值等問題，故并非M越大越好。

針對此問題，引入一種非線性自適應淘汰個體比例，即在初始迭代時對種群邊緣的麻雀加大淘汰比例，節(jié)省搜索時間，在迭代后期逐漸減小，保持種群的多樣性，其更新方式如式（10）所示：

其中，M 為淘汰個數；t 為當前迭代次數；Tmax為最大迭代次數；ω 為下降速率；Eli∈（0，0.5）為依據具體要求設定的初始淘汰比例；P 為種群總數；

取Tmax=500，ω 為1.5，Eli 分別為0.2 與0.4，P 為100，其自適應淘汰曲線如圖3 所示。

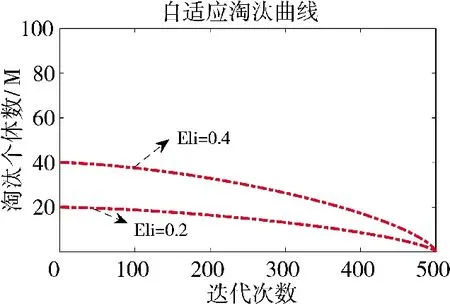
圖3 不同初始淘汰比例下的淘汰曲線Fig.3 Elimination curves under different initial elimination ratios

2.3 基于柯西變異的跟隨者位置更新

經過加入淘汰機制，每次迭代適應度最差的一部分麻雀個體會被直接淘汰，在最優(yōu)值附近產生，所以其在下一代位置更新時，大概率會進入發(fā)現者群體中，并執(zhí)行式（3），由于麻雀種群中發(fā)現者與跟隨者的比例是不變的，故相應的一部分發(fā)現者會變?yōu)楦S者并執(zhí)行式（4），并且跟隨者會在發(fā)現者附近覓食。為了平衡算法前期淘汰機制不斷在最優(yōu)值附近產生的缺陷、防止算法陷入局部最優(yōu)值，受文獻［10］啟發(fā)改進跟隨者位置更新公式，用來提高全局搜索能力，其更新方式如式（11）。

當i＞n/2 時，表明當前個體處于種群邊緣，其適應度值排在末位，所以要加大其搜索范圍，使其向更廣闊的區(qū)域進行覓食。

而對于適應度值排在靠前位置的跟隨者，引入柯西變異。Cauchy（0，1）為標準的柯西分布函數，比標準正態(tài)分布能產生更大的擾動，使其在最優(yōu)值附近進行相對廣泛的搜索。TESSA 算法流程如下頁圖4 所示。

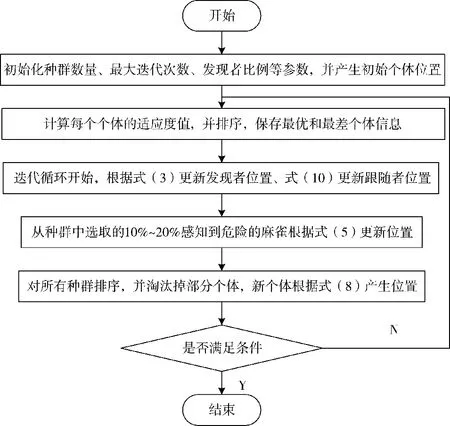
圖4 TESSA 算法流程圖Fig.4 TESSA algorithm flowchart

3 TESSA 算法性能測試

為驗證TESSA 對于提高函數尋優(yōu)速度、尋優(yōu)精度和穩(wěn)定性的效果，選取灰狼優(yōu)化算法（GWO）、粒子群優(yōu)化算法（PSO）、麻雀搜索算法（SSA）、融合正余弦和柯西變異的麻雀搜索算法（SCSSA）、與本文加入淘汰機制的麻雀搜索算法（TESSA）在6 個測試函數上進行仿真比較［10］。

3.1 測試函數選取

選取6 個測試函數進行仿真，為了確保算法性能的穩(wěn)定性，其中f1～f4為單峰測試函數，其搜索范圍分別為［-100，100］、［-10，10］、［-100，100］、［-100，100］，f5、f6為多峰測試函數，其搜索范圍為［-5.12，5.12］、［-32，32］。在單峰函數上的測試可以用來檢測算法的尋優(yōu)速度與精度。在多峰函數上，則用來驗證其跳出局部最優(yōu)的能力。測試函數表達式如表2 所示。

表2 測試函數表達式Table 2 Test function expression

3.2 TESSA 性能對比分析

將加入淘汰機制的麻雀搜索算法（TESSA）與融合正余弦和柯西變異的麻雀算法（SCSSA）［10］、基本麻雀算法（SSA）［8］、粒子群算法（PSO）［14］、灰狼算法（GWO）［5］在6 個基準函數上進行尋優(yōu)測試，各個算法公共參數即種群數量均設置為50，最大迭代次數Tmax為200，搜索范圍依據測試函數上下界。5 種算法參數選取如表3 所示時，經實驗，各個算法參數選取在6 個測試函數上均能達到其自身尋優(yōu)仿真的最佳效果。

表3 算法參數設置Table 3 Algorithm parameter settings

取最優(yōu)值、平均值、標準差作為實驗結果數據，最優(yōu)值反映了算法跳出局部最優(yōu)解的能力，平均值體現了尋優(yōu)精度，標準差則代表了算法的穩(wěn)定性。

由于函數維度變化時，對于算法尋優(yōu)能力的要求會增大，每個維度之間也會有一定的相互干擾，為了證明不同維度下TESSA 的優(yōu)越性，函數求解維度分別設置為30 和80。各個算法獨立運行50 次，以降低實驗的偶然性。仿真采用環(huán)境為intel-i5 處理器，2.30 GHz，16 GB 內存，MATLAB R2018b。

5 種算法在6 個測試函數下獨立運行50 次的實驗結果如下頁表4 所示。由表4 中的仿真數據可以看出：對于單峰測試函數f1～f3，TESSA 都能收斂至最優(yōu)值，且平均值與標準差均為0，而SCSSA 在f2中未能達到最佳效果，這展示出了TESSA 良好的尋優(yōu)精度。對于f4中的高維空間，TESSA 最優(yōu)值雖與SCSSA 相差一個數量級，但其平均值與標準差效果較好，這體現出TESSA 在穩(wěn)定性方面的優(yōu)勢。在f5、f6多峰測試函數中，TESSA、SCSSA、SSA 的尋優(yōu)精度都達到了最優(yōu)，且標準差都為0，故麻雀搜索算法相較于灰狼算法和粒子群算法具有更佳的函數尋優(yōu)能力。

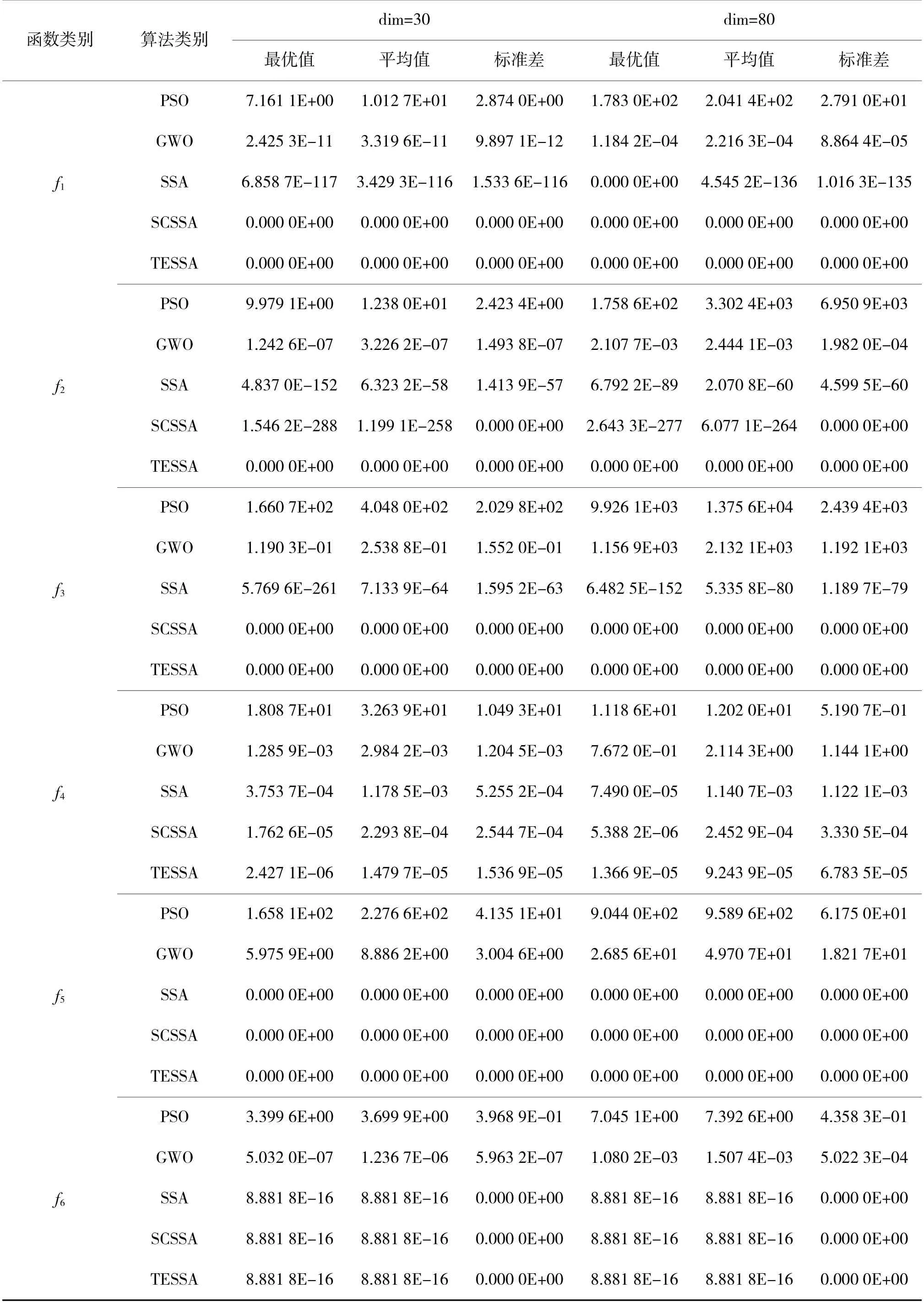
表4 算法性能比較Table 4 Comparison of algorithm performance

為體現TESSA 較其他兩種麻雀搜索算法在收斂速度方面的優(yōu)勢，畫出了各算法在6 個測試函數維度均為30 時的迭代收斂曲線，如第71 頁圖5 所示。

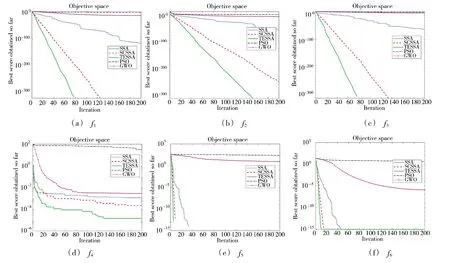
圖5 5 種算法在函數上的收斂曲線Fig.5 Convergence curve of five kinds of algorithms on functions

圖5（a）～圖5（d）為單峰測試函數的算法收斂曲線，圖5（e）和圖5（f）為多峰測試函數收斂曲線。由圖5（a）可以看出當TESSA 和SCSSA 都能夠收斂至最優(yōu)值時，TESSA 的收斂速度更快，在79 代便收斂至極小值，而SCSSA 需要迭代126 代。由圖5（b）可知，在5 種算法中，只有TESSA 達到最優(yōu)值，體現了其尋優(yōu)精度。圖5（d）中，當5 種算法都未能尋優(yōu)至最優(yōu)值時，TESSA 仍然保持著與其他算法相比更快的收斂速度與全局搜索能力。從圖5（e）與圖5（f）中則看出在多峰函數測試下，雖然SCSSA 改善了傳統(tǒng)麻雀算法的一些缺陷，性能有大幅提高，但TSEEA 仍在保持精度與穩(wěn)定性的同時具有更快的尋優(yōu)速度。

3.3 Wilcoxon 秩和檢驗

威爾科克森（Wilcoxon）秩和檢驗是一種非參數統(tǒng)計檢驗方法，本文用來檢測TESSA 與其他4 種算法是否具有非隨機性的顯著優(yōu)勢。Wilcoxon 秩和檢驗將在5%的顯著性水平下進行檢驗，當檢驗結果P＜0.05 時，拒絕H0假說，表明對比的兩種優(yōu)化算法在尋優(yōu)能力上存在著顯著差別；當P ＞0.05 時，接受H0假說，表明進行對比的兩種算法在尋優(yōu)效果上沒有區(qū)別。

在6 個測試函數（30 維）上TESSA 算法與其他4 種算法的Wilcoxon 秩和檢驗P 值如表5 所示；由表5 結果可知，大多數P 值＜0.05，證明TESSA 與其他算法具有顯著性差異。在f1～f4中P 值均大幅小于5%，故TESSA 尋優(yōu)性能高于SCSSA、SSA、PSO、WOA。在f5、f6中TESSA 較SCSSA 尋優(yōu)效果差異不明顯，但在其他4 種測試函數中性能顯著優(yōu)于SCSSA，可以說明改進的有效性。

表5 Wilcoxon 秩和檢驗的P 值Table 5 P-values of Wilcoxon rank sum test

4 結論

本文對基本麻雀搜索算法（SSA）在高緯復雜系統(tǒng)中收斂速度下降，無法平衡局部收斂與全局搜索等問題，提出了一種加入淘汰機制的麻雀搜索算法（TESSA）。在初始化種群位置時，引入分段Tent 混沌映射，來提高種群的多樣性。在跟隨者位置處，加入了一種基于柯西變異的自適應位置更新公式。最后在當代種群位置更新完后，增加了淘汰機制，并采用了非線性的淘汰個體比例。經過與其他4 種算法在6 個基準函數上的測試仿真后，結果表明，TESSA 改善了傳統(tǒng)麻雀搜索算法的諸多問題，平衡了收斂速度與尋優(yōu)精度，相較于其他改進后的麻雀搜索算法有一定性能方面上的提升。

在未來進一步的深入學習中，重點研究方向為將TESSA 應用于實際，優(yōu)化工程中的控制、解耦等方面，證明其解決具體問題的有效性。