一種動態不確定海洋環境下的USV 態勢自主感知及避障算法

王 瀲，陳 霄，完顏娟

（1.解放軍91054 部隊，北京 102442；2.軍事科學院，北京 100091）

0 引言

無人艇作為一種小型的海上無人智能平臺，具有高速機動、靈活隱蔽的特點，可潛入敵區，展開情報獲取工作，實現對關切海域的持續監視。此外，USV 還可用于反潛、掃雷、電子戰、海上搜救、海洋科考、執法取證、后勤支援等軍用和民用領域，具有廣泛的應用前景［1-3］。在USV 自主執行各項任務過程中，需要實時對其附近海洋環境進行態勢感知，收集靜態和動態障礙物等信息，來實現對各類障礙物的安全躲避，以此確保所肩負任務的順利完成［4-5］。

無人艇避障算法種類很多，包括Dijkstra、D*、A*、人工勢場法、快速隨機搜索樹、速度障礙法等［6-9］。周則興等提出了一種基于改進人工勢場法的USV 避障算法，通過引入自衰減斥力場解決了期望航向角突變和抖動的問題，仿真對比結果表明了算法的先進性［10］。張金澤等提出一種密集障礙物海況下的USV 自主避障算法，該算法基于模糊推理的改進型雙窗口動態窗口法設計實現，仿真實驗表明該算法能有效避免USV 從密集障礙物群外繞行，避障路徑更加合理［11］。竇強為解決無人作戰艇在未知海域避碰規劃問題，借鑒柵格法和人工勢場法，設計實現了一種基于導航雷達回波視頻的實時避碰規劃算法，并通過仿真和實際試驗證明了算法是可行的［12］。劉漸道等提出一種融合避碰規則的動態窗口法來解決USV 在海上航行時的自主避障問題，充分考慮開始避障的時機、避讓的轉向幅度以及何時進行復航等因素，仿真實驗驗證算法的可行性［13］。

無人艇等水面航行器在實際海洋環境中航行時，主要會受到風、浪、流等不確定因素的影響。通常情況下，為了確保無人艇自身能夠按照預定的航線和設定的航速航行，通常分兩種情況考慮海洋環境的動態不確定性：一方面無人艇通過裝備的風向、風速、海流等傳感器，實時感知海洋環境的動態變化，通過航跡跟蹤控制算法實時補償校準，確保無人艇更準確地跟蹤航線，主要需要考慮風向、風速、海流等傳感器的測量誤差；另一方面無人艇通過搭載的雷達等傳感器，實時感知周圍障礙物的情況，預測動態障礙物的運動軌跡，以在合適的時間啟動恰當的避障算法，實現對障礙物的準確躲避，主要需要考慮雷達等傳感器測量誤差、觀測漂移和動態障礙物隨機運動不確定性。本文主要研究USV態勢自主感知及避障算法，因此，考慮采用已經對風向、風速、海流等傳感器的測量誤差進行了補償校準的航跡跟蹤控制算法，例如文獻［14］中的算法，主要考慮傳感器測量誤差、觀測漂移和動態障礙物隨機運動不確定性這一類因素。

本文針對USV 在動態不確定海洋環境下的態勢自主感知和實時避障問題，充分考慮傳感器測量誤差、觀測漂移和動態障礙物隨機運動不確定性，對相關誤差進行不確定性建模，設計了一種融合COLREGs 海事規則的USV 態勢自主感知及避障算法，給出了算法詳細的流程設計圖，并通過正面相遇、追越、左右交叉相遇4 種典型的場景，對本文提出的算法進行了仿真實驗驗證，仿真結果表明了本文所提出的考慮COLREGs 規則和動態不確定海洋環境下的USV 態勢自主感知及避障算法的有效性。

1 三類海事規則

如圖1 所示，以USV 航向為基準，定義追越、交叉相遇和正面相遇3 個場景。追越：若USV 與障礙物的航向差在［0°，45°）和［315°，360°）區間，若有碰撞威脅，USV 須從障礙物左側通過。交叉相遇：若USV 與障礙物航向差在［45°，165°］區間，若有碰撞威脅，USV 須左側航行躲避；若差值在（195°，315°）區間，若有碰撞威脅，USV 須右側航行躲避。正面相遇：若USV 與障礙物的航向角度差值在（165°，195°］區間，若有碰撞威脅，USV 須右側航行躲避。

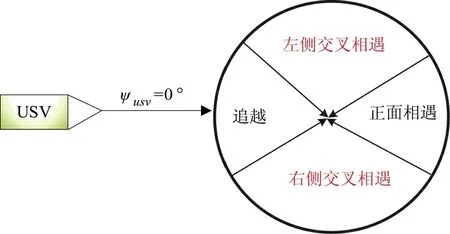
圖1 沖突場景定義Fig.1 The definitions of conflict scenes

2 融合COLREGs 規則的速度障礙法

定義使用COLREGs 規則的時機是十分困難的，當前學術界和工業界均沒有精確標準，本文采用判定距離L0，以此來觸發COLREGs 規則的啟用時機。具體如下：若USV 與障礙物之間的距離大于L0，則不進行避讓；若USV 與障礙物之間的距離小于L0，當存在碰撞危險時，則遵循COLREGs 規則啟用局部動態路徑規劃，USV 局部動態路徑規劃采用融入COLREGs 規則的速度避障法。

如下頁圖2 所示，假設障礙物為圓形并進行適度膨脹（非圓形可采用其外接圓表示），USV 相對于障礙物的速度為V=VA-VB，以USV 的位置為頂點，向障礙物作切線l1，l2，定義兩切線間為錐形碰撞區并記為VO，即V 處于兩切線之間時，必會碰撞。對于多個障礙物，VO 域記為多個障礙物計算后VOi的集合，即，m 為障礙物的個數。當USV 的速度矢量與VO 域有重疊部分且距離小于等于L0時，USV 立即改變航向或速度以脫離碰撞區。

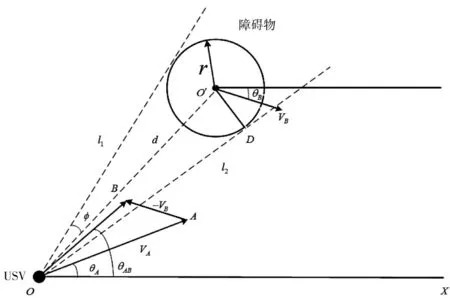
圖2 速度障礙法Fig.2 Velocity obstacle avoidance algrithm

以障礙物在USV 的左側為例，假定t=i 時刻，已知障礙物的速度為VB，航向為θB，USV 的速度為VA，航向為θA，障礙物的半徑為r，其與USV 之間的距離為d，且與USV 的連線OO'與X 軸之間的夾角為α，則，。根據余弦定理可得：

1）對于執行精確循跡任務的USV 和轉向困難或轉向代價較大的大型USV，在探測到未知障礙物時，可只改變航速，不改變航向。首先，求解相撞時的速度，其中，d 為USV 與障礙物間的距離，可通過傳感器獲取，T 為時間周期。之后，根據避障要求確定速度的改變量。若要求以避障最短時間為首要目標，則，dmin最小安全距離；若以安全為首要保證，則，dmax為最大安全距離。

2）根據COLREGs 規則，改變USV 的航向，可分為USV 航向、航速均改變和僅改變USV 航向兩種情況，需要根據其與障礙物的相遇場景來選定，具體設計如下：當USV 與障礙物相遇場景為“追越”時，在根據COLREGs 規則改變USV 航向的同時，USV 的期望速度設計為原期望航速的1.5 倍；當USV 與障礙物相遇場景為“交叉”時，在根據COLREGs 規則改變USV 航向的同時，USV 的期望速度設計為原期望航速的0.5 倍；當USV 與障礙物相遇場景為“正面相遇”時，USV 的期望速度設計為原期望航速的0.5 倍。

避障結束后，USV 根據自身所在的位置和原全局路徑規劃的航線信息，在恰當的跟蹤控制算法的作用下，恢復到原航線上，繼續自主航行。

3 信息的不確定性建模

由于USV 航行在復雜時變的海洋環境中，障礙物運動具有一定的不確定性，且USV 航行中對障礙物位置和運動的探測都依靠各類傳感器，如雷達、測速儀等，無法避免地存在測量誤差或漂移等問題。因此，在USV 態勢自主感知及避障過程中，須對傳感器測量誤差和障礙物隨機運動導致的不確定性進行建模。

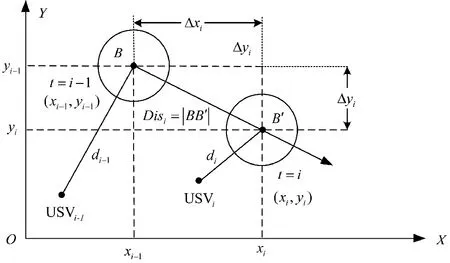
圖3 不同時刻的障礙物位置Fig.3 The obstacle location at different times

式中，θ 為待估計的參數，Θ 為其取值范圍。假設X的樣本值為，則的聯合分布率為。設定的樣本值為，則事件發生的概率為：

極大似然函數為：

由式（8）解得：

由此可得μ，σ2的極大似然估計量分別為：

同理，應用極大似然法估計Δv 和Δθ 的期望和方差：

在正態分布中，根據“3σ”法則約有99.7%的值分布在均值μ 附近3 個標準差σ 的區域內。

4 考慮不確定信息的USV 態勢自主感知及避障算法

如下頁圖4 所示，在t=i 時，根據t=1，2，…，i-1時刻障礙物的狀態，對t=i 時刻障礙物的速度矢量建模，并利用第3 章中的方法估計出t=i 時刻的由此求得t=i 時的和。根據“3σ”法則，t=i 時和的大小分別在區間內。障礙物速度矢量變化最大時，不確定性最高，據此確定其二次膨脹半徑R，從而將不確定性轉化為確定性。此外，由圖4 中幾何關系可得：

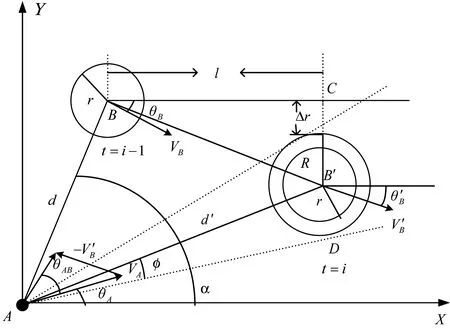
圖4 考慮障礙物不確定性的情況Fig.4 The situation considering uncertain information about obstacles

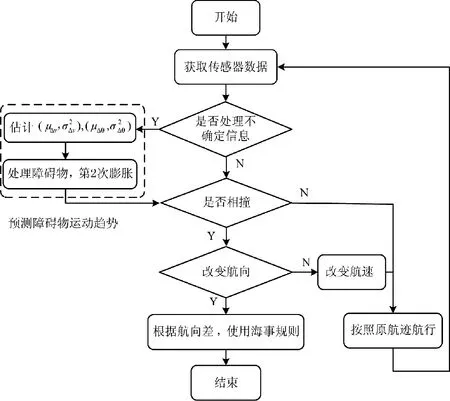
圖5 考慮COLREGs 規則和不確定性信息的USV 局部路徑規劃流程圖Fig.5 The local path planing flow chart of USV considering COLREGs rules and uncertain information

5 仿真實驗與分析

考慮USV 在沿全局路徑航行時對未知動態和靜態障礙物的避障問題，如圖6 所示，紅色區域為已知的靜態障礙物，為模擬動態障礙物運動的不確定性，其速度變化量為Δv=0.2 kn，變化范圍為［-2，2］kn；角度變化量設置為Δθ=2°，變化范圍為［-15°，15°］，在t=i 時，根據t=1，2，…，i-1 時刻障礙物的運動狀態，利用第3 章中的方法估計出t=i 時刻的，由此求得t=i 時的和。根據“3σ”法則確定障礙物的二次膨脹半徑。取判定距離L0=80 m，最小和最大安全距離為dmin=20 m，dmax=80 m。本章分4 種典型的相遇場景進行仿真實驗。

圖6 USV 與障礙物正面相遇Fig.6 USV encountering the obstacle face to face

5.1 正面相遇和追越場景

障礙物設置如下：

障礙物1：起始點位置坐標（350，210），航速為10 kn，航向為220°，t=10 s 時，障礙物開始運動；

障礙物2：起始點位置坐標（850，500），航速為6 kn，航向為35°，t=85 s 時，障礙物開始運動。

USV 的初始航速仍設定為20 kn，全局路徑起始點為A，終止點為B，從圖6 可以看出，USV 通過對障礙物一段時間內（本節仿真中從障礙物開始運動時刻開始計算）運動不確定性航向、航速數據進行不確定性建模，得到膨脹半徑，據此對障礙物進行二次膨脹，如圖6 中紅色虛線圓所示。

當USV 距離障礙物1 80 m 時，USV 判定會遇場景為正面相遇，并立即開始進行局部路徑規劃進行自主避障，依據COLREGs 規則，USV 從被超越障礙物的右舷處航行通過。如下頁圖7 所示，可以看到USV 在障礙物的右側規劃出了一條局部避障路徑，并在航跡跟蹤控制算法的作用下，通過跟蹤規劃好的局部路徑，實現了對障礙物的右舷超越，之后USV 能夠繼續沿任務之初規劃好的全局路徑航行。

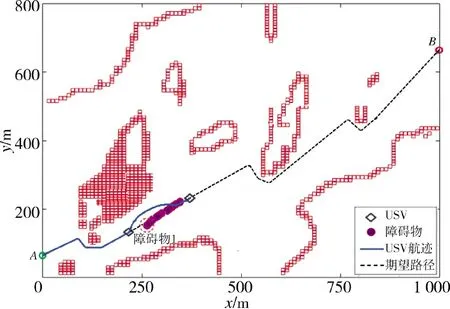
圖7 正面相遇下USV 自主避障Fig.7 The autonomous obstacle avoidance of USV in head-on encounter

USV 在沿全局路徑航行過程中，實時檢測未知障礙物，如圖8 所示，當USV 距離障礙物2 80 m時，USV 判定會遇場景為追越并開始進行局部路徑規劃，依據COLREGs 規則，當存在碰撞危險時，要求USV 從被超越障礙物的左舷處安全通過，如圖9所示，可以看到USV 在障礙物的左舷規劃出了一條局部避障路徑，并在航跡跟蹤控制算法的作用下，通過跟蹤規劃好的局部路徑，實現了對障礙物的左舷超越，之后USV 能夠繼續沿任務之初規劃好的全局路徑航行。

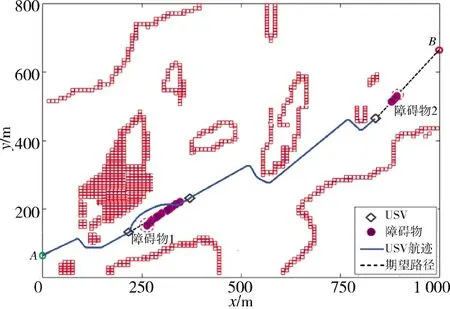
圖8 USV 與障礙物追越場景仿真圖Fig.8 The overtaking scene simulation diagraph between USV and the obstacle

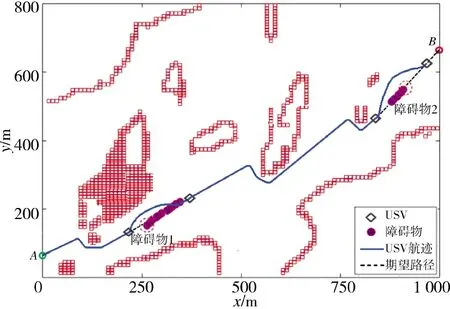
圖9 追越場景下USV 自主避障Fig.9 The autonomous obstacle avoidance of USV under overtaking scene

5.2 左右交叉相遇場景

障礙物設置如下：

障礙物3：起始點位置坐標（295，375），航速為15 kn，航向為145°，t=20 s 時，障礙物開始運動；

障礙物4：起始點位置坐標（750，305），航速為12 kn，航向為325°，t=60 s 時，障礙物開始運動。

同樣地，USV 全局路徑的起始點為A，終止點為B，初始航速仍設定為20 kn，從圖10 可以看出，USV 通過對障礙物一段時間內運動不確定性航向、航速數據進行不確定性建模，得到膨脹半徑，據此對障礙物進行二次膨脹，如圖10 中紅色虛線圓所示。

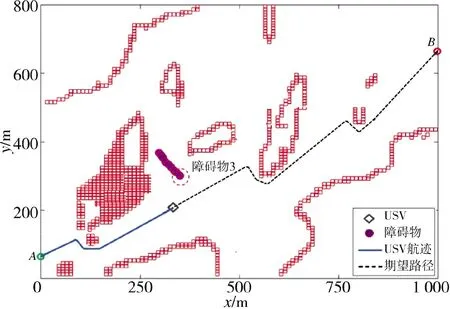
圖10 USV 與障礙物左交叉相遇場景仿真圖Fig.10 The left cross encounter scene simulation diagraph between USV and obstacle

當USV 距離障礙物3 80 m 時，USV 判定會遇場景為左交叉相遇并開始進行局部路徑規劃，依據COLREGs 規則，當存在碰撞危險時，要求USV 左側航行躲避。如圖11 所示，可以看到USV 在原航行路線的左側規劃出了一條局部避障路徑，并在航跡跟蹤控制算法的作用下，通過實時跟蹤規劃好的局部路徑，實現了對障礙物的有效躲避，之后USV 能夠繼續沿任務之初規劃好的全局路徑航行，并實時檢測未知障礙物。

圖11 左交叉場景下USV 自主避障Fig.11 The autonomous obstacle avoidance of USV under left cross scene

如圖12 所示，當USV 距離障礙物4 80 m 時，USV 判定會遇場景為右交叉相遇并開始進行局部路徑規劃，依據COLREGs 規則，當存在碰撞危險時，要求USV 右側航行躲避，如圖13 所示，可以看到USV 在原航行路線的右側規劃出了一條局部避障路徑，并在航跡跟蹤控制算法的作用下，通過實時跟蹤規劃好的局部路徑，實現了對障礙物的有效躲避，之后USV 能夠繼續沿任務之初規劃好的全局路徑航行，并實時檢測未知障礙物，直至安全到達全局路徑的終點。仿真結果表明了本文所提出的考慮COLREGs 規則和動態不確定海洋環境下的USV態勢自主感知及避障算法的有效性。

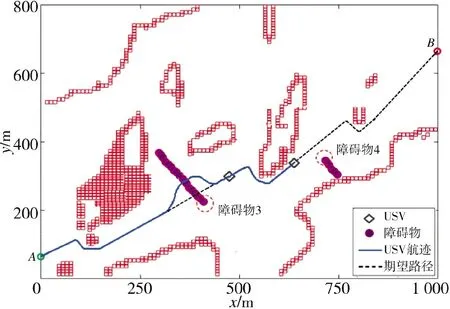
圖12 USV 與障礙物右交叉相遇場景仿真圖Fig.12 The right cross encounter scene simulation diagraph between USV and the obstacle

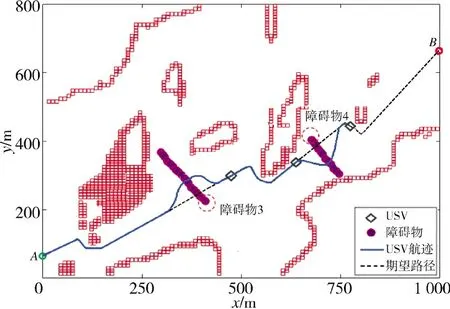
圖13 右交叉場景下USV 自主避障Fig.13 The autonomous obstacle avoidance of USV under right cross scene

6 結論

本文針對USV 在動態不確定海洋環境下的態勢自主感知和實時避障問題，設計了一種融合COLREGs 海事規則的USV 態勢自主感知及避障算法，該算法充分考慮了傳感器測量誤差和障礙物隨機運動不確定性，對相關誤差進行不確定性建模，并通過正面相遇、追越、左右交叉相遇4 種典型的場景進行仿真實驗證明了算法的先進性和有效性。

本文提出的算法融合了真實的海上航行規則，且擁有較強的穩定性和較低的計算量，在工程實踐中具備很好的指導意義。與此同時，對我國USV 相關航行避障技術和相關避障系統等裝備的研制具有一定的理論指導和現實意義。