基于BO-LSTM 神經網絡的地面無人系統網絡時延分析

王鑫鑫，田衛萍，田 野，劉 超，黨國龍

（北方自動控制技術研究所，太原 030006）

0 引言

近年來，隨著機器學習、人工智能、遠程控制、云計算、自主協同等前沿科學技術在無人系統領域的發展，催生了地面無人系統的跨越式變革［1］，地面無人系統由系統架構、運動規劃、環境感知、自主控制、安全防護等多種關鍵技術融合而成［2］。某地面反無人機系統主要包括操控終端和地面反無人機作業車，具體組成如圖1 所示。

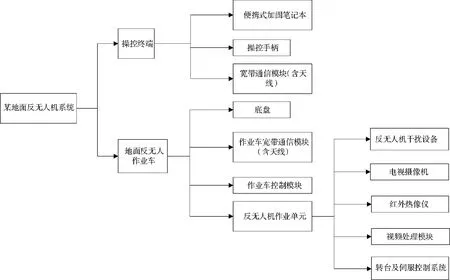
圖1 某地面反無人機系統組成圖Fig.1 Composition diagram of a ground anti drone system

目前常見的地面無人系統的通信方式主要是遙控數據鏈［3］，為實現操作人員對多個地面無人車輛的集群控制，無線通信網絡的引入是必然的發展趨勢。但由于網絡中各節點共享通信帶寬，隨著節點數量以及不同任務的差異，網絡時延也會發生變化，從而影響操控系統的實時性和精度。

本文對某地面反無人機系統的傳輸時延進行分析，針對網絡時延的隨機分布特性，建立貝葉斯算法（BO）優化的長短期記憶（LSTM）神經網絡時延預測模型，并在實驗測試獲得的網絡時延樣本數據集上對預測的效果進行驗證。

1 網絡控制地面反無人機系統

地面反無人機系統通信網絡結構圖如圖2 所示。操控終端和地面反無人作業車之間通過基站實現無線通信。地面反無人作業車電視攝像機和紅外熱像儀對無人機目標進行探測和跟蹤，采集并生成無人機目標視頻圖像信息，通過基站分配的無線信道回傳給操控終端，同時，多線激光雷達等傳感器采集的地面反無人作業車位置信息，網絡攝像頭采集的周邊環境信息也通過基站分配的無線信道回傳給操控終端。操控終端通過基站分配的無線信道發送操控指令，控制地面反無人作業車的行進，以及伺服轉臺的轉動，實現對無人機目標的探測、跟蹤和干擾。

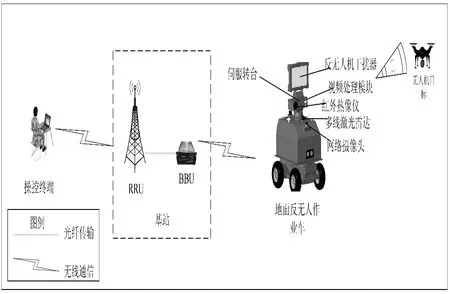
圖2 地面反無人機系統通信網絡結構圖Fig.2 Communication network structure diagram of ground anti-UAV system

地面反無人機系統網絡控制流程圖如圖3 所示。

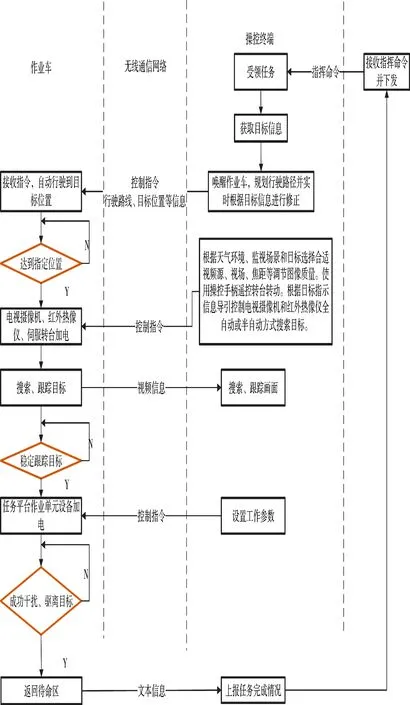
圖3 系統工作流程圖Fig.3 Flow chart of system operation

系統工作流程如下：

1）班組操作人員通過操控終端接收上級指揮中心下發的作業命令、目標位置信息，在對作業車上電后，根據作業車上傳的車體位置信息，規劃并實時修正行進路線，通過無線通信網絡發送給作業車，驅動作業車行駛至指定位置，同時，操控終端接收作業車上傳的視頻信息。

2）作業車到達指定位置后，根據目標位置信息、周邊環境信息，選擇合適的視頻源、視場、焦距等參數調節視頻圖像質量，通過操控手柄控制轉臺轉動，使目標在光電跟蹤設備視場內成像，計算目標在視場內的位置與視軸中心的偏移量，輸出脫靶量信息，設置轉臺方位軸和俯仰軸的轉動速度，通過無線通信網絡發送給伺服控制系統進行補償，將目標導引到視場視軸中心，完成對目標的探測和識別。

3）在探測和識別到目標后，由伺服控制系統控制光電跟蹤設備對目標進行自動跟蹤，在能夠穩定跟蹤后，設置作業單元的工作參數，完成對目標的干擾、迫降或驅離，然后，由操控終端向上級指揮中心上報任務完成情況。

2 地面反無人機系統時延分析

無線通信網絡以基站為接入節點，在操控終端和地面反無人作業車上集成寬帶通信模塊，操控終端和地面反無人作業車之間通過基站實現通信。

無線通信網絡工作帶寬最大為20 MHz，可以接入至少64 個終端設備，支持語音調度、視頻調度、視頻監控、文件傳輸等功能。

無線通信網絡具有以下幾個方面的特點：1）區域寬帶無線通信網絡通信覆蓋范圍廣，跨空間性高，能夠克服空間和地域的限制，只要有網絡的接入點，相應的軟硬件，就可以構成可靠的控制系統；2）在無線通信網絡中可以接入其他終端，擴展更多不同類型的業務。

相對地，由于無線通信網絡本身帶寬和上下行時隙配比，以及在各時隙上傳輸業務劃分的原因，數據（尤其是數據量大的視頻數據）在操控終端和作業車之間發送和接收需要花費較多的時間，此外，在數據傳輸的過程中，不可避免地會有數據碰撞和數據重傳等問題的產生，也會增加傳輸的時延。由數據傳輸所造成的時延，主要包括數據信號的采集、量化、編碼、壓縮、解碼以及顯示的過程。

傳輸時延的存在會影響數據傳輸的實時性，使得整個地面反無人機系統存在滯后性，不能及時對任務目標情況作出決策和響應，從而會降低系統的控制性能質量，影響系統的穩定性，此外，傳輸時延的存在還會使系統發生空采樣和多采樣等問題。

在實際執行任務時，地面反無人作業車回傳目標視頻圖像至操控終端，操作人員根據目標視頻圖像向地面反無人作業車發送操控指令，而視頻圖像信息回傳和操作控制指令的傳輸過程，各個環節都會產生時延，具體時延組成如圖4 所示。

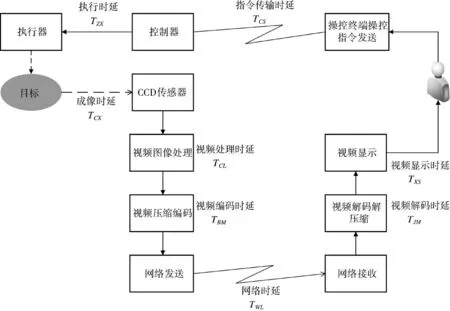
圖4 地面反無人機系統時延組成圖Fig.4 Time delay composition diagram of ground anti-UAV system

由圖4 可知，地面反無人機系統網絡控制的時延主要由兩部分組成，第一部分是視頻圖像信息回傳過程的時延，設為TH，另一部分是操控終端操作控制指令的傳輸時延，設為TK，則TH和TK可以由式（1）和式（2）表示，系統總時延T 可以由式（3）表示。

如圖5 所示，以無人機目標在CCD 傳感器上開始成像為起點，經過TH時間，無人機目標在操控終端上成像，操作人員通過操控終端向作業車發送控制指令，經過TK時間，作業車根據控制指令，開始對無人機目標進行跟蹤和干擾。從無人機目標在作業車CCD 傳感器上成像到作業車開始跟蹤和干擾，總時延如式（3）所示，TH和TK在時間上具有連續性，TK的產生在TH時刻之后。

圖5 地面反無人機系統時延關系圖Fig.5 Time delay relationship diagram of ground anti-UAV system

式（1）中，TCX是地面反無人作業車上，反無人機作業單元電視攝像機和紅外熱像儀中CCD 傳感器采集目標視頻圖像幀的時間，TCL是視頻圖像幀信號經過視頻圖像處理板處理的時間，TBM是視頻編碼器對視頻圖像進行壓縮、量化和編碼的時間，TWL是視頻圖像通過無線通信網絡，從地面反無人作業車發送到操控終端接收的時間，TJM是操控終端在接收到視頻圖像后經過解碼、反量化和解壓的時間，TXS是視頻圖像在解碼為視頻幀信號后在顯示器上輸出顯示的時間。

式（2）中，TCS是在看到視頻畫面后，操作人員通過操控終端發送操作控制指令到作業車控制模塊接收的時間，TZX是地面反無人作業車在接收到操作控制指令后，發送控制指令控制伺服電機驅動轉臺轉動的時間。

在上述時延中，伺服電機的執行時延TZX相對較小，在進行系統時延分析時，一般不考慮TZX的影響，可以忽略不計；操作人員在看到視頻圖像后，通過操控終端采集操控手柄轉動信號，編碼然后通過無線通信網絡發送，操控手柄轉動信號數據量相對很小，指令傳輸時延TCS可以忽略不計；由于視頻圖像數據量很大，視頻壓縮編碼和解碼的時間會相對較長，同時，無線通信網絡帶寬較窄，因為其他業務節點的存在，分配給視頻信號傳輸的時隙較小，視頻回傳時延TH較大，因此，本文對系統時延的分析主要是圍繞視頻回傳的時延TH展開。

在視頻回傳的時延TH中，成像時延TCX、視頻處理時延TCL、視頻編碼時延TBM、視頻解碼時延TJM、視頻顯示時延TXS都以幀為單位進行采集和處理，成像時延、視頻處理時延和視頻顯示時延取決于CCD傳感器、視頻處理板和顯示器的硬件結構和性能，當硬件結構和性能不發生變化時，每一幀圖像經過采集、處理和顯示的時間是固定的；視頻編解碼是對視頻圖像幀進行壓縮和重建的過程，以一部分完整幀圖像為基準，對每一幀中的運動目標的位置變化作殘差運算，最后獲得的是一部分完整幀圖像以及若干殘差幀，當采用的視頻編解碼器和編解碼標準不變時，對每一幀的壓縮比例是一樣的，最后獲得的幀數據量基本相同，因此，視頻編解碼時延是基本固定的；網絡時延TWL與無線通信網絡的結構、當前網絡中接入的業務節點的數量、當前業務信道資源的占用情況等有關，當網絡的結構不發生變化時，隨著業務數據量變化和信道時隙的分配，網絡時延會在一定范圍內隨機變化。

3 地面反無人機系統網絡時延預測

網絡時延TWL是在一段時間內維持在一個區間內波動的隨機時延，而且，在這一區間段內，網絡時延具有很強的自相關性，下一時刻的時延與前一段時間的時延存在一定的非線性關系［4］，正因為這種非線性和相關性，網絡時延在局部范圍內是可預測的。

目前，對于網絡時延數據的預測方法主要包括傳統的概率統計模型、人工智能模型以及混合模型等。傳統的概率統計模型包括自回歸模型、滑動平均模型、自回歸滑動平均模型等［5-6］，具有結構簡單、計算量小、計算時間短的特點，但對于復雜度較高的時間序列數據，該模型預測精度較難保證。人工智能模型主要有決策樹、支持向量機以及神經網絡等［7-8］，神經網絡又包括BP 神經網絡、RBF 神經網絡、RNN 神經網絡等，神經網絡是在數據預測領域的最新方法，且預測精度很高。混合模型是將各個預測算法和模型組合起來，共同對數據進行預測，可以補充單一預測模型的不足之處。

本文采用貝葉斯算法（BO）優化的長短期記憶（LSTM）神經網絡對處理后的網絡時延數據進行預測，LSTM 神經網絡相較于BP 神經網絡、RBF 神經網絡、RNN 神經網絡等，改善了對數據序列的長期依賴問題，緩解了在訓練時反向傳播帶來的“梯度消失”問題，同時，其內部網絡中“門”結構的設置，可以將數據的重要特征保存下來，可以實現對數據序列中數據趨勢和前后相關性的挖掘，在對時間序列數據的處理和分析上具有很大優勢。

3.1 自相關性檢驗

時延預估的前提是時延數據序列具有隨機性，而且當前時刻的數據與歷史數據相關，即時延數據序列具有自相關性，因此，在對時延數據進行分析和預測時，首先要對時延數據序列的自相關性進行檢驗。

對于一組時間序列是否具備自相關性，是通過自相關系數進行判斷的，而自相關系數是通過自相關函數（ACF）獲取的。時間序列的樣本自相關函數的計算公式為

式中，rk是自相關系數，t 為時間序列數據的時序，k為時間滯后步長，n 表示時間序列樣本數據長度，xt為時間序列在t 時刻的數值，xt+k為時間序列t 時刻滯后k 個步長時（t+k）時刻的數值，時間序列變量的均值可由式（5）進行計算。

利用式（4）和式（5），可以對時間序列數據逐個計算出自相關系數，再由這些自相關系數組成自相關系數變化圖，由自相關函數變化圖可以看出時間序列數據是否具備自相關性。

3.2 LSTM 神經網絡

LSTM 神經網絡［9］，是一種特殊的RNN 循環神經網絡，關鍵在于“記憶細胞”的狀態，通過設計“門”結構可以去除或者增加信息到“記憶細胞”狀態，“門”是一種讓信息選擇式通過的方法，主要包括輸入門、輸出門和遺忘門，后續的幾乎所有LSTM神經網絡的設計和應用都是以這三種“門”結構為基礎的。LSTM 神經網絡結構如下頁圖6 所示。

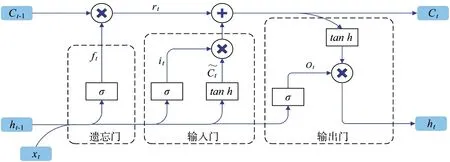
圖6 LSTM 神經網絡結構圖Fig.6 LSTM neural network structure diagram

1）遺忘門。遺忘門決定了將要從“細胞”狀態中丟棄哪些信息，計算公式為：

式中，Wfh、Wfx、bf是遺忘門的權重，ht-1為上一時刻的輸出，xt為當前時刻的輸入，σ 為激活函數。

2）輸入門。輸入門是確定需要將怎么樣的新的信息保存到“細胞”狀態中，計算公式為：

式中，WCh、WCx、bC是待加入“細胞”狀態的信息的權重。

3）輸出門。輸出門是確定當前時刻隱藏層的輸出ht，該輸出是基于當前時刻的“細胞”狀態過濾后的數值，計算公式為：

式中，Woh、Wox、bo是輸出門的權重。

3.3 貝葉斯算法（BO）優化LSTM 神經網絡

LSTM 神經網絡的構建需要確定的超參數眾多，超參數的選取對LSTM 神經網絡模型的訓練過程有很大的影響。在LSTM 神經網絡模型的訓練過程中，超參數通常由人為進行選取和調整，缺乏規律性，偶然性的成分居多，需要人為地對參數進行大量的調整和實驗，且不易獲得最優的超參數和訓練結果，因此，采用貝葉斯算法對訓練LSTM 神經網絡過程中的超參數進行優化。

貝葉斯算法是對待優化函數進行近似的一種模型，是一種非常有效的全局優化方法，目標是尋找到全局最優解，主要思想是給定一個待優化的目標函數，該函數是廣義的函數，只需給定輸入和輸出即可，無需知道函數的內部結構和數學性質，然后根據貝葉斯定理估計待優化目標函數的后驗概率分布，同時，通過不斷地添加樣本數據對待優化目標函數的后驗概率分布進行更新，即根據對目標函數過去參數信息的評估，更好地調整當前的參數信息。

核心過程主要包括概率代理模型（先驗函數）和采集函數。

用貝葉斯算法優化LSTM 神經網絡時延預測模型的流程如圖7 所示。

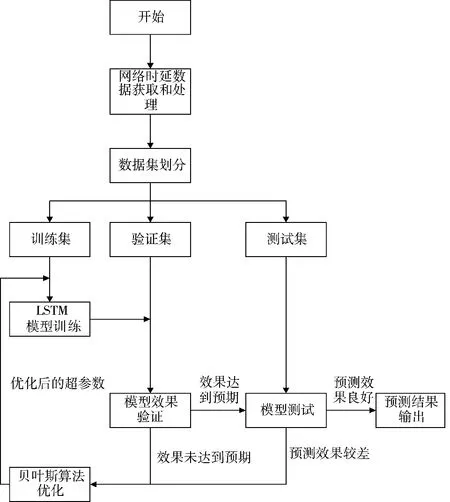
圖7 貝葉斯算法優化的LSTM 預測模型構建圖Fig.7 Construction diagram of LSTM prediction model optimized by Bayesian algorithm

LSTM 神經網絡模型訓練的過程相當于優化損失函數的過程，在設定超參數后，通過帶入訓練集數據，對LSTM 神經網絡的權重進行更新，使得LSTM 神經網絡的輸出，損失函數達到最小值，貝葉斯算法的優化是為了選取最優的超參數，以提高LSTM 神經網絡的訓練效果。

貝葉斯算法優化LSTM 神經網絡超參數的過程，首先，根據超參數的取值范圍，隨機產生初始的參數樣本數據，代入到高斯過程中，對LSTM 模型進行訓練，利用損失函數的值對高斯模型進行修正，使其更能擬合實際的數據分布；然后，選取新的一組超參數樣本數據代入高斯模型，對LSTM 神經網絡進行訓練，輸出對應的損失函數值，若符合要求，則該組超參數樣本值即為最優的超參數，若不符合要求，則重新選取超參數樣本數據代入高斯模型，對LSTM 神經網絡進行訓練，直到輸出的損失函數值符合要求。

3.4 模型評價標準

為了驗證貝葉斯算法優化LSTM 神經網絡時延預測模型對網絡時延數據預測的精確性，采用決定系數（R2）、均方根誤差（RMSE）和平均絕對誤差（MAE）來衡量，計算公式如式（12）～式（14）所示。

4 網絡時延預測模型驗證

4.1 網絡時延數據樣本

利用地面反無人作業車、操控終端和基站設備構建地面反無人機系統，在調整地面反無人作業車和操控終端時鐘同步的情況下，地面反無人作業車發送帶有時間戳的視頻幀圖像，發送時刻記為T1，操控終端接收時刻記為T2，則網絡時延為TWL=T2-T1。

通過上述測量方法進行測試，共獲得1 000 組網絡時延數據，如圖8 所示。

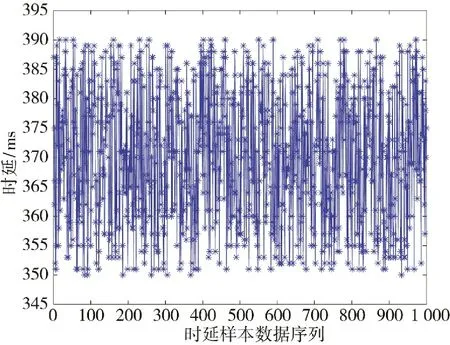
圖8 網絡時延測試樣本序列圖Fig.8 Sample sequence diagram for network time delay test

4.2 自相關性檢驗

基于4.1 節測量得到的網絡時延數據，由式（4）和式（5）計算自相關系數，畫出自相關系數變化圖，如圖9 所示。

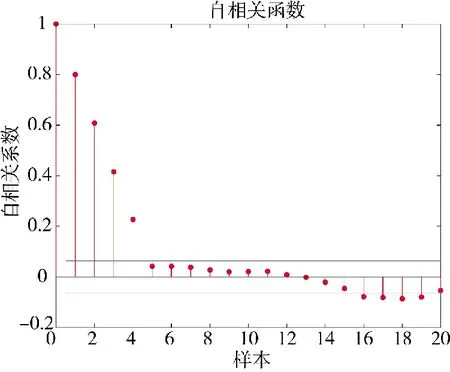
圖9 網絡時延自相關系數變化圖Fig.9 Graph of changes in network time delay autocorrelation coefficients

當計算得到的自相關系數取值為1 時，時間序列數據為完全正相關；取值為-1 時，時間序列數據為完全負相關；取值為0 時，時間序列數據不具備相關性。由圖8 可知，實驗測試采集到的1 000 組網絡時延數據序列自相關系數顯著不為0，表明該組數據具備自相關性，每組時延數據之間存在關聯。因此，可以利用實驗測得的網絡時延數據進行后續時延預測。

4.3 數據預處理

為提高模型的預測精度，采用平滑估計［10］的方法對上述數據進行處理，在處理過程中利用了“中位數”是均值的魯棒思想，起到對數據類似于過濾的效果，具體步驟如下：

處理后的時延樣本序列如下頁圖10 所示。

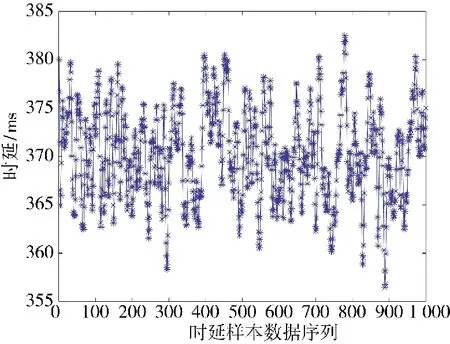
圖10 處理后的網絡時延樣本數據序列Fig.10 Processed network time delay sample data sequences

采用方差（δ2）來衡量圖8 中網絡時延數據序列和圖10 中經過平滑估計處理后的網絡時延數據序列的整體波動情況，方差計算公式如式（16）所示。

式中，μ 為樣本數據的平均值，N 為樣本數據個數。

方差值越小，樣本數據的整體波動越小，表明數據變化趨勢更加平滑和穩定，能夠更好地分析出數據的變化規律，能夠更好地進行預測。

上述圖8 和圖10 兩組數據的方差計算情況如表1 所示。

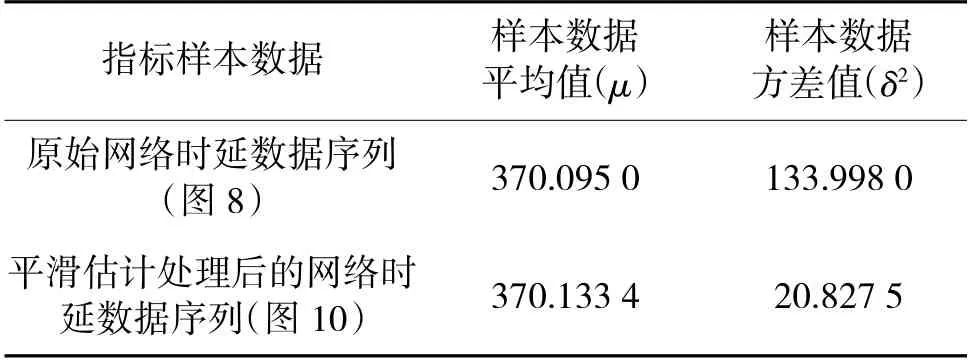
表1 圖8 和圖10 兩組數據方差計算情況Table 1 Calculation of variance for two sets of data in Fig.8 and 10

由表1 可知，經過平滑估計處理的網絡時延數據序列方差值小于原始網絡時延數據序列方差值，表明平滑估計的數據處理方法能夠過濾數據，降低樣本數據的整體波動，從而提升對數據的分析和預測效果。

設定模型的輸入維度為15，預測步長為1，即以連續的15 組網絡時延數據作為歷史數據，預測下一時刻的時延數據，與數據集中的第16 組數據進行對比。因此，劃分后新的網絡時延數據集共有985 組數據，每一組數據都由16 列數據組成，前15列為模型的輸入，最后一列數據與模型的輸出數據進行對比。

將新的985 組網絡時延數據集按照7∶3 的比例劃分為訓練集和測試集，其中，訓練集又以8∶2的比例劃分出驗證集數據。將訓練集、驗證集和測試集數據進行歸一化處理。

4.4 LSTM 神經網絡搭建

在基于網絡時延數據樣本搭建LSTM 預測模型時，需要對模型的輸入層、隱含層和輸出層的結構進行設計，同時，還要考慮模型在進行訓練和預測時超參數的設置，訓練時超參數的選取和設置如表2 所示。

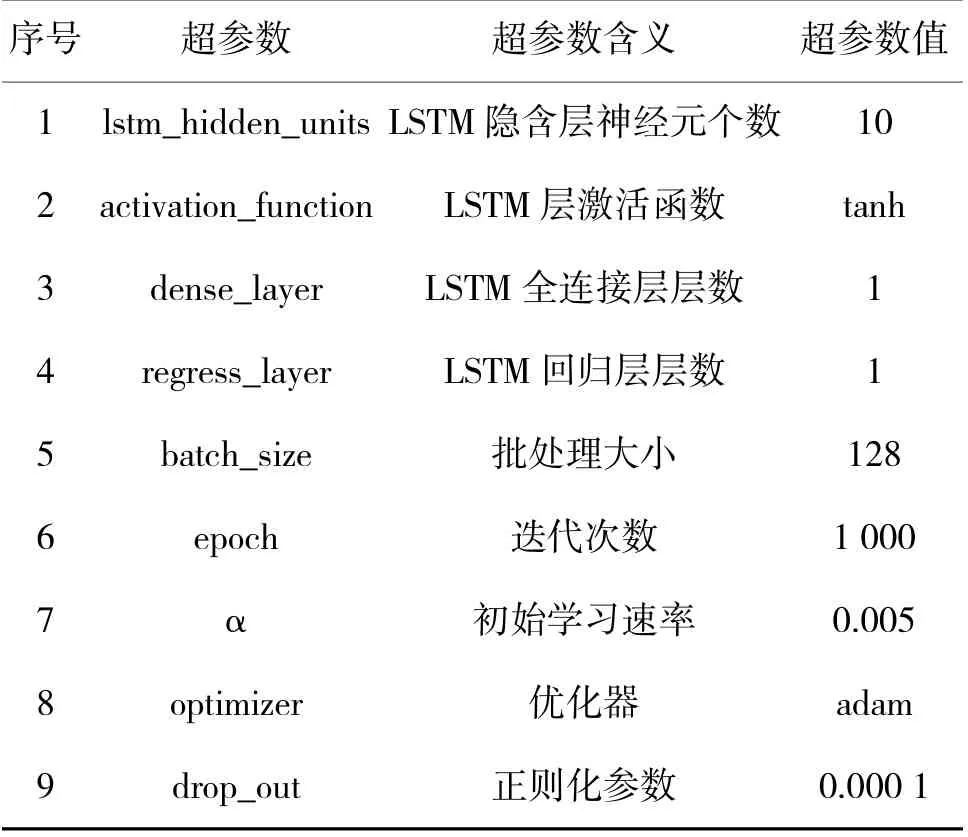
表2 LSTM 模型訓練超參數選取和設置表Table 2 LSTM model training hyperparameter selection and setting table

貝葉斯算法優化超參數的重點為隱含層層數、初始學習速率和正則化參數，激活函數選用tanh 函數，全連接層和回歸層層數還是設置為一層，優化器選用adam 優化器，批處理大小和迭代次數根據經驗公式進行設置。

4.5 貝葉斯算法優化LSTM 神經網絡超參數

以交叉驗證過程中用于評估訓練的模型對驗證集數據符合程度的均方差（MSE）指標作為貝葉斯算法優化的目標函數。

待優化的超參數約束范圍如表3 所示。

表3 超參數約束范圍表Table 3 Hyperparameter constraint range table

設定貝葉斯優化算法的迭代更新次數為30次，優化過程如下頁表4 所示。

表4 超參數優化過程表Table 4 Hyperparameter optimization process table

在第27 次迭代時，目標函數值最小，此時，對應的超參數即為最優值，將其代入LSTM 神經網絡進行訓練和測試。

4.6 實驗結果分析

在測試集上對訓練好的模型的預測效果進行測試，預測和評估結果如圖11 和表5 所示。

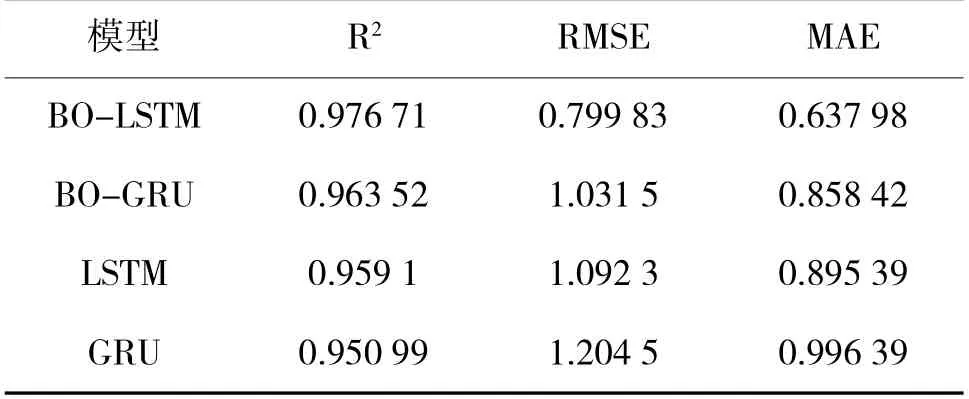
表5 不同預測模型評估結果對比Table 5 Comparison of evaluation results of different prediction models

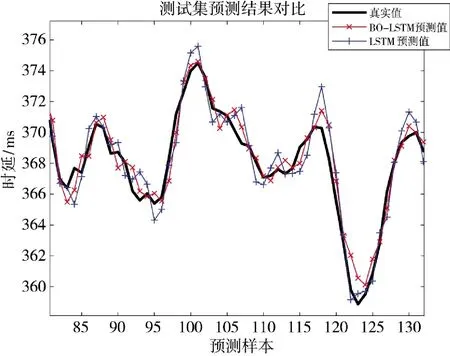
圖11 BO-LSTM 和LSTM 預測結果對比Fig.11 Comparison of prediction results between BO-LSTM and LSTM

從圖10 的預測結果和表4 中BO_LSTM 和LSTM 模型的決定系數（R2）可以看出，貝葉斯算法優化的LSTM 預測模型在測試集上的預測值，相較于LSTM 預測模型，更貼合測試集實際數據，驗證了貝葉斯算法在優化超參數問題的有效性。

為進一步驗證貝葉斯算法優化的LSTM 預測模型的有效性，采用了GRU 神經網絡，并利用貝葉斯算法優化相同的超參數，將預測結果進行對比，預測結果的對比如圖12 所示。

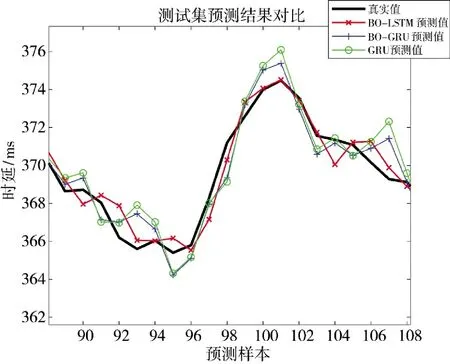
圖12 不同模型預測結果Fig.12 Prediction results of different models

GRU 神經網絡隱含層的神經元個數gru_hidden_units=21，初始學習速率α=0.009 761 2，正則化參數drop_out=1.027 9e-5。

不同預測模型的評估結果如表5 所示。

由表5 可知，當用決定系數（R2）來評估時，這4種預測模型的R2值都在95%以上，都可以很好地對測試集數據進行擬合，其中，BO-LSTM 預測模型的R2值最高，表明其擬合效果最好，GRU 預測模型的R2值最低，其擬合效果相對較差。

當用均方根誤差（RMSE）和平均絕對誤差（MAE）來評估時，BO-LSTM 預測模型的RMSE 和MAE 值最小，表明該模型預測精度最高，模型效果最好，GRU 模型的RMSE 和MAE 值最小，表明該模型預測精度最低，模型效果最差。BO-LSTM 模型相較于BO-GRU 模型，RMSE 值減小了22.46%，MAE值減小了25.68%，LSTM 模型相較于GRU 模型，RMSE 值減小了9.32%，MAE 值減小了10.14%，表明了LSTM 模型效果優于GRU 模型。BO-LSTM 模型相較于LSTM 模型，RMSE 值減小了26.78%，MAE 值減小了28.75%，BO-GRU 模型相較于GRU模型，RMSE 值減小了14.36%，MAE 值減小了13.85%，表明貝葉斯算法對模型的優化是有效的。

5 結論

針對通過無線通信網絡通信的某地面反無人機系統，分析了系統在工作過程中傳輸時延的產生與組成，針對網絡時延隨機變化的特性，提出了一種貝葉斯算法（BO）優化的LSTM 神經網絡時延預測模型，將實驗測試獲得的網絡時延數據劃分為訓練集和測試集，先用訓練集訓練模型，然后利用訓練好的模型在測試集上進行測試，并將預測結果與GRU 和BO-GRU、LSTM 預測方法進行對比，通過對比，BO 優化的LSTM 神經網絡時延預測模型預測精度更高，預測效果更好，驗證了該預測模型的有效性。