基于循環(huán)神經(jīng)網(wǎng)絡(luò)的彈藥著速預(yù)測(cè)

王現(xiàn)磊，王義江，陳春江，吳家健

（解放軍63861 部隊(duì)，吉林 白城 137001）

0 引言

在武器系統(tǒng)試驗(yàn)靶場(chǎng)，獲取高精度彈道參數(shù)是評(píng)定和分析武器打擊精度的重要內(nèi)容［1］。而彈藥的著速是影響目標(biāo)毀傷程度的重要參數(shù)之一，因此，精準(zhǔn)獲取彈藥的著靶速度成了重要研究目標(biāo)。目前靶場(chǎng)大多采用梳狀靶、電探針等區(qū)截裝置接觸式測(cè)量法［2］，測(cè)量值與真值相差較大；高速攝影裝置可以對(duì)彈藥飛行過(guò)程實(shí)時(shí)記錄其影像，但人工判讀底片過(guò)程，不可避免引入一定程度的測(cè)量誤差［3］；連續(xù)波測(cè)量雷達(dá)是獲取彈藥徑向速度的重要途徑，具有測(cè)速精度高的優(yōu)點(diǎn)，但是立靶對(duì)雷達(dá)回波信號(hào)產(chǎn)生較大噪聲和干擾，后續(xù)對(duì)彈藥著速的提取依賴于信號(hào)的濾波、特征點(diǎn)的提取以及對(duì)數(shù)據(jù)處理的經(jīng)驗(yàn)，其精度受到不同程度影響。本文通過(guò)使用雷達(dá)采集的時(shí)間速度序列數(shù)據(jù)，將循環(huán)神經(jīng)網(wǎng)絡(luò)應(yīng)用于彈藥著速的預(yù)測(cè)，以期提高彈藥著速的精確性，具有較大的理論意義。

彈藥飛行的速度數(shù)據(jù)，具有三大特性：隨機(jī)性、連續(xù)性和周期性。當(dāng)前時(shí)間點(diǎn)的速度受到溫度、風(fēng)速等空氣動(dòng)力學(xué)因素的影響，速度數(shù)據(jù)具有隨機(jī)性；相鄰時(shí)間速度的值是連續(xù)的，具有時(shí)間依賴性，因此，具有連續(xù)性；周期性是指時(shí)間速度數(shù)據(jù)呈某種趨勢(shì)的現(xiàn)象，因此，將速度數(shù)據(jù)作為時(shí)間序列進(jìn)行分析與預(yù)測(cè)具有可行性，利用RNN 對(duì)彈藥著速進(jìn)行預(yù)測(cè)，并與RFR 算法和基于BP 的MLP 模型預(yù)測(cè)結(jié)果進(jìn)行對(duì)比，取得了滿意的擬合效果，對(duì)彈藥后續(xù)指標(biāo)的評(píng)估具有實(shí)用價(jià)值。

1 時(shí)間序列預(yù)測(cè)

時(shí)間序列預(yù)測(cè)的方法主要包括基于數(shù)學(xué)理論模型的預(yù)測(cè)方法和基于大數(shù)據(jù)驅(qū)動(dòng)預(yù)測(cè)方法［4］。數(shù)學(xué)理論模型預(yù)測(cè)方法主要基于數(shù)學(xué)和統(tǒng)計(jì)學(xué)等知識(shí)，僅從時(shí)間的維度對(duì)被預(yù)測(cè)對(duì)象建模，對(duì)復(fù)雜時(shí)間序列數(shù)據(jù)難以建立精確的數(shù)理統(tǒng)計(jì)模型，適用性受到極大限制且預(yù)測(cè)精度大大降低。基于大數(shù)據(jù)驅(qū)動(dòng)預(yù)測(cè)的方法主要有傳統(tǒng)機(jī)器學(xué)習(xí)方法、前饋神經(jīng)網(wǎng)絡(luò)方法和循環(huán)神經(jīng)網(wǎng)絡(luò)等［5］。傳統(tǒng)的機(jī)器學(xué)習(xí)方法，如線性回歸、支持向量機(jī)、隨機(jī)森林等算法［6-8］，對(duì)于時(shí)間序列的處理，是利用數(shù)據(jù)中的維度特征，進(jìn)而構(gòu)建起從因變量到目標(biāo)預(yù)測(cè)值的函數(shù)方程，通過(guò)不斷優(yōu)化構(gòu)建的損失函數(shù)，來(lái)構(gòu)造回歸模型。但是該類(lèi)模型在建模時(shí)僅考慮時(shí)間序列當(dāng)前時(shí)間點(diǎn)的特性，忽略了數(shù)據(jù)彼此間具有時(shí)間依賴性，因此，預(yù)測(cè)精度不高。

神經(jīng)網(wǎng)絡(luò)是一種由大量運(yùn)算節(jié)點(diǎn)之間互相連接構(gòu)成的運(yùn)算模型。每個(gè)節(jié)點(diǎn)代表一種特定的輸出函數(shù)，即激勵(lì)函數(shù)。每?jī)蓚€(gè)節(jié)點(diǎn)間的連接都代表一個(gè)對(duì)于通過(guò)該連接信號(hào)的加權(quán)值，稱之為權(quán)重，這相當(dāng)于人工神經(jīng)網(wǎng)絡(luò)的記憶。網(wǎng)絡(luò)的輸出則以網(wǎng)絡(luò)的連接方式、權(quán)重值和激勵(lì)函數(shù)的不同而不同。而網(wǎng)絡(luò)自身通常都是自然界某種算法或者函數(shù)的逼近，也可能是一種邏輯策略的表達(dá)［9］。神經(jīng)網(wǎng)絡(luò)模型的神奇點(diǎn)就在于它是一個(gè)“黑盒”模型，輸入大量歷史數(shù)據(jù)，模型就可以自動(dòng)學(xué)習(xí)到序列之間的規(guī)則以及依賴關(guān)系。神經(jīng)網(wǎng)絡(luò)方法彌補(bǔ)了傳統(tǒng)統(tǒng)計(jì)模型固有的劣勢(shì)，可以處理具有非線性模式數(shù)據(jù)。根據(jù)需要，僅對(duì)前饋神經(jīng)網(wǎng)絡(luò)做簡(jiǎn)單介紹。

2 前饋神經(jīng)網(wǎng)絡(luò)

2.1 多層感知機(jī)

人工神經(jīng)網(wǎng)絡(luò)（artificial neural network，ANN）由神經(jīng)生理學(xué)家Warren McCulloch 和數(shù)學(xué)家Walter Pitts 于1943 年首次提出，通過(guò)對(duì)生物神經(jīng)元進(jìn)行建模，首次提出了一種形式神經(jīng)元模型；1957 年Frank Rosenblatt 提出了感知機(jī)，感知機(jī)是最簡(jiǎn)單的ANN架構(gòu)，能夠確定神經(jīng)元的連接權(quán)重，但無(wú)法解決線性不可分問(wèn)題，基于此人們提出了MLP 模型，也稱為前饋網(wǎng)絡(luò)模型。MLP 通常采用3 層結(jié)構(gòu)，由輸入層、隱藏層及輸出層組成。如圖1 所示。

圖1 多層感知機(jī)模型Fig.1 Multi-layer perceptron model

輸入層表示神經(jīng)元接受x1，x2，…，xn作為輸入，隱藏層通過(guò)權(quán)重與輸入層的各單元相連接，通過(guò)激勵(lì)函數(shù)計(jì)算隱藏層各單元的輸出值，同樣通過(guò)權(quán)重與輸出層相連接。由于模型的輸出與模型自身之間不存在反饋過(guò)程，因此，被稱為前饋神經(jīng)網(wǎng)絡(luò)。

2.2 誤差反向傳播算法

1986 年 David Rumelhart、Geoffrey Hinton 和Ronald Williams 發(fā)表的開(kāi)創(chuàng)性文獻(xiàn)［10］介紹了誤差反向傳播訓(xùn)練算法，該算法能夠針對(duì)每個(gè)模型參數(shù)計(jì)算網(wǎng)絡(luò)誤差的梯度，并通過(guò)比較實(shí)際輸出和期望輸出得到誤差信號(hào)E，把誤差信號(hào)從輸出層逐層向前傳播得到各層的誤差信號(hào)，再通過(guò)調(diào)整各層的連接權(quán)重以減小誤差。其權(quán)重的調(diào)整主要結(jié)合梯度下降法，過(guò)程如圖2 所示。

圖2 梯度下降法Fig.2 Gradient descent method

通過(guò)實(shí)際輸出和期望輸出之間的誤差E 和梯度，確定連接權(quán)重w0調(diào)整值，得到新的連接權(quán)重w1，然后反復(fù)不斷地調(diào)整權(quán)重以使誤差E 達(dá)到最小，并從中學(xué)習(xí)得到最優(yōu)的權(quán)重連接wopt，即網(wǎng)絡(luò)收斂到最優(yōu)解。

3 著速預(yù)測(cè)網(wǎng)絡(luò)模型

3.1 模型介紹

著速預(yù)測(cè)網(wǎng)絡(luò)模型是一個(gè)從序列到向量的網(wǎng)絡(luò)，由連續(xù)波雷達(dá)采集的時(shí)間速度數(shù)據(jù)作為輸入序列，并忽略彈藥著速外的所有輸出，即忽略飛行過(guò)程的速度值，輸出著靶速度。其模型按時(shí)間展開(kāi)的網(wǎng)絡(luò)如圖3 所示。

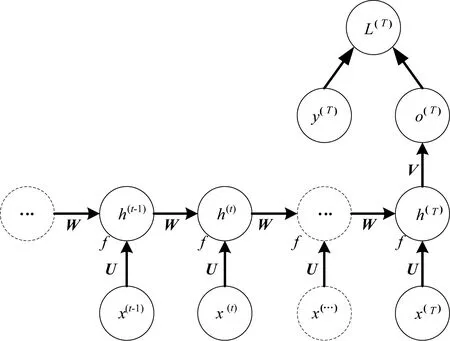
圖3 時(shí)間展開(kāi)的網(wǎng)絡(luò)模型Fig.3 Network model of time expansion

圖3 為含有一層循環(huán)神經(jīng)網(wǎng)絡(luò)、若干隱藏節(jié)點(diǎn)的著速預(yù)測(cè)模型。其中，損失衡量序列結(jié)束時(shí)的輸出與相應(yīng)的訓(xùn)練目標(biāo)的距離；U 表示RNN輸入層到隱藏層的連接權(quán)重矩陣，W 表示隱藏到隱藏的循環(huán)連接權(quán)重矩陣；V 表示隱藏到輸出的連接權(quán)重矩陣；f 為激活函數(shù)；為記憶單元且滿足式（1），即在時(shí)間步長(zhǎng)t 時(shí)刻遞歸神經(jīng)元的輸出是先前時(shí)間步長(zhǎng)中的所有輸入函數(shù)

式中，b 為偏置向量。

3.2 評(píng)價(jià)指標(biāo)

為量化實(shí)驗(yàn)結(jié)果便于比較，本文選取了預(yù)測(cè)問(wèn)題的典型性能指標(biāo)均方根誤差（RMSE），其公式如下：

4 實(shí)驗(yàn)及結(jié)果分析

4.1 數(shù)據(jù)集說(shuō)明

實(shí)驗(yàn)選用某型穿甲彈連續(xù)波雷達(dá)采集并處理后的速度數(shù)據(jù)共計(jì)60 發(fā)，作為實(shí)驗(yàn)數(shù)據(jù)集，每發(fā)彈的數(shù)據(jù)格式為等間隔的、連續(xù)的81 個(gè)時(shí)間速度點(diǎn)，其中，最后一點(diǎn)為彈藥著靶速度。隨機(jī)選取42 發(fā)（占70%）作為訓(xùn)練集，6 發(fā)作為驗(yàn)證集，剩余12 發(fā)（占20%）作為測(cè)試集。樣本輸入特征（x_train，x_valid，x_test）為［42，80，1］，即總共42 發(fā)數(shù)據(jù)，每發(fā)前80 個(gè)點(diǎn)作為輸入樣本，維度為1；輸出特征（y_train，y_valid，y_test）為［42，1，1］，即每發(fā)彈藥的著靶速度，共計(jì)42 發(fā)。

4.2 模型超參數(shù)設(shè)置及訓(xùn)練

激活函數(shù)選擇不同會(huì)導(dǎo)致梯度不穩(wěn)定問(wèn)題，通過(guò)控制變量方法，為著速預(yù)測(cè)網(wǎng)絡(luò)模型選取ReLU 激活函數(shù)，并使用其初始化策略即He 初始化；對(duì)比常規(guī)梯度下降優(yōu)化器，選取Adam 優(yōu)化器加快訓(xùn)練速度，由于Adam 是一種自適應(yīng)學(xué)習(xí)率算法，因此，不對(duì)學(xué)習(xí)率超參數(shù)η 進(jìn)行調(diào)整，使用其默認(rèn)值η=0.001。

本實(shí)驗(yàn)中多層感知機(jī)模型和預(yù)測(cè)網(wǎng)絡(luò)模型的隱藏層數(shù)（n_hidden）與每層包含的神經(jīng)元數(shù)（n_neurons），采取RandomizedSearchCV 探索超參數(shù)空間，如表1 所示。

表1 超參數(shù)空間Table 1 Hyperparametric space

設(shè)置n_hidden：［0，1，2，3］，n_neurons 為［0，100］，設(shè)置最大迭代次數(shù)為200，當(dāng)損失值連續(xù)10 次未發(fā)生改變或至最大迭代次數(shù)時(shí)，嘗試其他超參數(shù)組合，結(jié)束并輸出最佳超參數(shù)組合。

經(jīng)過(guò)RandomizedSearchCV 探索超參數(shù)空間，多層感知機(jī)模型和著速預(yù)測(cè)網(wǎng)絡(luò)模型返回最佳超參數(shù)組合及超參數(shù)設(shè)置如表2 所示，根據(jù)訓(xùn)練過(guò)程，兩個(gè)模型epoch 在90 左右RMSE 值收斂于穩(wěn)定狀態(tài)，因此，設(shè)置epoch=110。

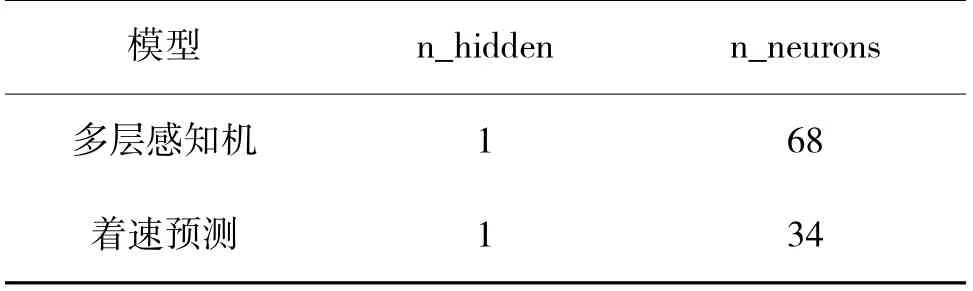
表2 最佳超參數(shù)組合Table 2 Best combination of hyperparametric

多層感知機(jī)模型和著速預(yù)測(cè)網(wǎng)絡(luò)模型訓(xùn)練過(guò)程中其訓(xùn)練樣本RMSE 曲線分別如圖4、圖5 所示；隨機(jī)森林回歸算法，通過(guò)調(diào)整參數(shù)訓(xùn)練樣本并對(duì)測(cè)試集進(jìn)行預(yù)測(cè)，其RMSE 值如表3 所示。從圖中可以看出，訓(xùn)練樣本在兩種模型中RMSE 最終均趨于穩(wěn)定的收斂狀態(tài)，其網(wǎng)絡(luò)學(xué)習(xí)過(guò)程較為類(lèi)似，相較而言著速預(yù)測(cè)網(wǎng)絡(luò)模型收斂速度更快；由表3 可直觀的看出著速預(yù)測(cè)網(wǎng)絡(luò)模型在測(cè)試集上的RMSE值相比其他兩種更小，即擬合效果更佳。

表3 測(cè)試集RMSE 值Table 3 RMSE values of test set

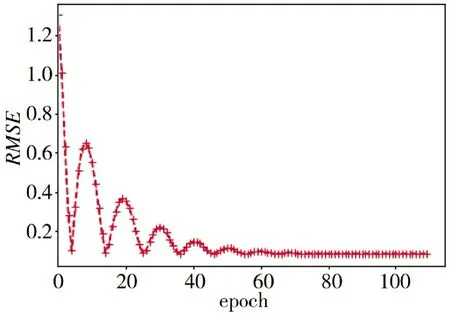
圖4 多層感知機(jī)訓(xùn)練過(guò)程Fig.4 Training process of multi-layer perceptron

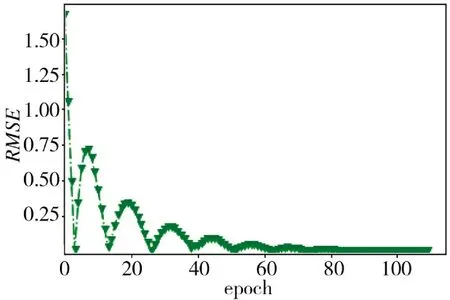
圖5 著速預(yù)測(cè)模型訓(xùn)練過(guò)程Fig.5 Training process of target velocity prediction model

著速預(yù)測(cè)模型真值與預(yù)測(cè)結(jié)果如圖6 所示，實(shí)驗(yàn)結(jié)果表明該模型的適用性較強(qiáng)，可通過(guò)網(wǎng)絡(luò)模型的不斷訓(xùn)練較準(zhǔn)確的學(xué)習(xí)出不同彈速的飛行規(guī)律，并給出精準(zhǔn)的預(yù)測(cè)，由后續(xù)的測(cè)試誤差圖可知，該模型具有很好的穩(wěn)定性。

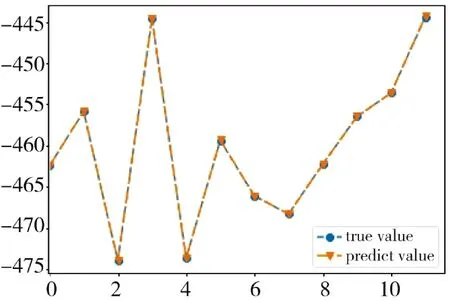
圖6 著速預(yù)測(cè)模型測(cè)試結(jié)果Fig.6 Test results of target velocity prediction model

為了直觀地對(duì)比3 種模型對(duì)彈藥著速的預(yù)測(cè)，實(shí)驗(yàn)測(cè)試集誤差結(jié)果如圖7～圖9 所示。

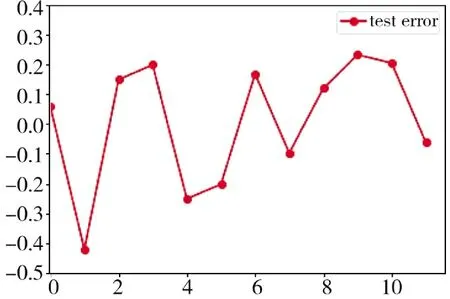
圖7 隨機(jī)森林測(cè)試誤差Fig.7 Random forest test errors

隨機(jī)森林回歸算法是一種基于集成學(xué)習(xí)的監(jiān)督式機(jī)器學(xué)習(xí)算法，通過(guò)加入不同或相同類(lèi)型算法獲取強(qiáng)大且穩(wěn)健的預(yù)測(cè)模型，且不易陷入過(guò)擬合；但因其隨機(jī)性，由圖7 可知預(yù)測(cè)結(jié)果不是很穩(wěn)定，有較大的波動(dòng)性，該算法對(duì)測(cè)試集著速預(yù)測(cè)誤差在0.2 左右。多層感知機(jī)模型，超參數(shù)空間較大且復(fù)雜，其隱藏層包含的神經(jīng)元數(shù)更多，通過(guò)選擇適宜的激活函數(shù)和超參數(shù)，基于BP 算法訓(xùn)練其模型用于著速預(yù)測(cè)，由圖8 可知，測(cè)試集著速預(yù)測(cè)誤差在0.15 左右，相比于隨機(jī)森林回歸算法預(yù)測(cè)精度和穩(wěn)定性得到改善，但預(yù)測(cè)結(jié)果穩(wěn)定性仍有起伏。而著速預(yù)測(cè)網(wǎng)絡(luò)模型受益于隱藏層之間有循環(huán)連接，考慮了速度數(shù)據(jù)之間存在時(shí)序上的依賴關(guān)系，極大地提高了網(wǎng)絡(luò)模型對(duì)速度數(shù)據(jù)的分析、學(xué)習(xí)能力和預(yù)測(cè)精度，且加快了網(wǎng)絡(luò)模型的訓(xùn)練速度，從而使網(wǎng)絡(luò)學(xué)習(xí)效果得到提高，由圖9 可知，其預(yù)測(cè)誤差絕對(duì)值在0.02 左右，且穩(wěn)定性更好；相比于前兩個(gè)算法模型，其預(yù)測(cè)精度有數(shù)量級(jí)的提升，取得了較好的實(shí)驗(yàn)效果，得到了更精確的預(yù)測(cè)結(jié)果。

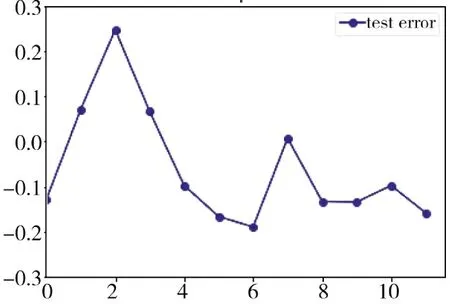
圖8 多層感知機(jī)測(cè)試誤差Fig.8 Multi-layer perceptron test errors

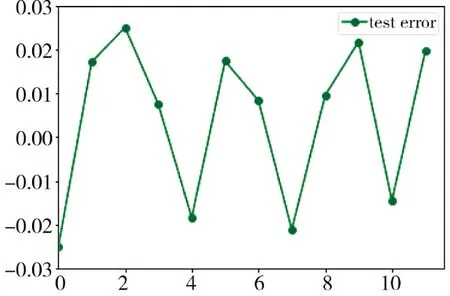
圖9 著速預(yù)測(cè)模型測(cè)試誤差Fig.9 Test errors of target velocity prediction model

5 結(jié)論

本文分別使用隨機(jī)森林回歸算法、基于BP 的多層感知機(jī)模型和基于RNN 的著速預(yù)測(cè)模型，對(duì)某型穿甲彈的著速進(jìn)行預(yù)測(cè)，從預(yù)測(cè)結(jié)果分析得出基于RNN 的預(yù)測(cè)模型，可更好地從速度數(shù)據(jù)中挖掘序列之間的內(nèi)部關(guān)聯(lián)且模型的適應(yīng)性較強(qiáng)，預(yù)測(cè)精度優(yōu)于傳統(tǒng)方法。實(shí)驗(yàn)結(jié)果表明，基于RNN 的著速預(yù)測(cè)模型，切實(shí)提高了分析預(yù)測(cè)效果，其預(yù)測(cè)結(jié)果可作為彈藥著靶速度。本文構(gòu)建的模型具有一定的應(yīng)用推廣價(jià)值，可推廣應(yīng)用于雷達(dá)測(cè)速數(shù)據(jù)跳點(diǎn)、丟失點(diǎn)的填補(bǔ)。