滾動還是滑動

馬小強　柳小林

［摘 要］從一道常見物理習題的解答過程入手，深化拓展題目所給條件，應用質心運動定律、剛體轉動定律分析均質小球繞球面運動的過程，計算小球運動過程中由無滑滾動變為有滑動滾動的臨界角度，通過圖像直觀地給出臨界角以及呈現此時大球面對小球的支持力隨球面間摩擦因數變化的關系。

［關鍵詞］無滑滾動；有滑滾動；臨界角；摩擦因數

［中圖分類號］? ? G633.7? ? ? ? ［文獻標識碼］? ? A? ? ? ? ［文章編號］? ? 1674-6058（2024）05-0050-03

一、習題呈現及解析

如圖1所示，光滑球面[A]固定在水平面上，其半徑為[R]。一個可以當作質點且質量為[m]的小球[B]放在球面A的頂部，由于受到擾動，小球B無初速地沿[A]的表面滑下，求小球[B]與球面[A]分離時的速度和位置。

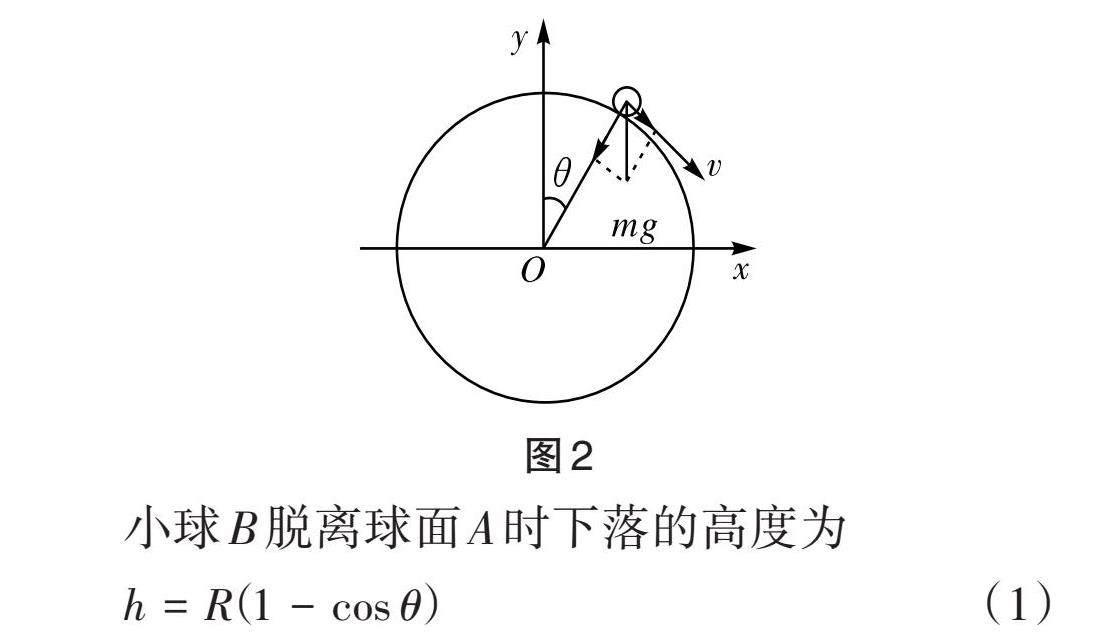
解析：小球[B]未脫離球面[A]之前做圓周運動，下滑過程中只有重力做功，小球[B]機械能守恒，小球[B]減少的重力勢能全部轉化為它的動能。假設當小球[B]在球面[A]上的偏離角度為[θ] 時，小球B與球面A脫離，脫離時，小球所受重力沿球面法線方向的分力提供做圓周運動的向心力（如圖2）。

小球B脫離球面A時下落的高度為

[h=R（1-cosθ）] ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （1）

設此時小球[B]的速度為[v]，根據機械能守恒定律可得：

[mgh=12mv2] ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （2）

圓周運動的向心力由重力的分力提供，則：

[mgcosθ=mv2R] ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（3）

聯立式（1）（2）（3），解得角度[θ]滿足[cosθ=2 3]， 即[θ=48.19°]。

結論：當小球B的偏離角度為[48.19°]時，小球B與球面A脫離，脫離時小球B的速度[v=2gR3]，下落高度[h=R 3]。

二、習題拓展分析

提出問題：如果小球不能當作質點，大球面不完全光滑，小球將如何運動？

定性分析：小球靜止在大球面頂端時，受到重力以及球面所施加的支持力，合力為零，處于不穩定平衡狀態。小球由于擾動一旦偏離平衡位置，則受重力mg、支持力[N]、與兩球面都相切的靜摩擦力[f] （為方便分析，將小球進行放大；如圖3）。

小球剛開始運動，角度[θ]較小，質心速率[vc]較小，小球法向加速度較小，重力的法向分量[mgcosθ] 較大，因此支持力[N]較大，此時所受靜摩擦力小于最大靜摩擦力[fmax=μsN]（其中[μs]為靜摩擦因數），小球做無滑滾動。一方面，隨著[θ]增大，小球所受支持力[N]和球面間的最大靜摩擦力減小；另一方面，由對瞬軸的角動量定理可知，隨著角度[θ]增大，小球重力對瞬軸的力矩逐漸變大，小球自身轉動的角速度和角加速度逐漸變大。另外，在質心的平動參考系中，重力和支持力對質心的力矩為零，由質心的角動量定理可知要使小球繞質心轉動的角加速度和角速度增加，必須要求靜摩擦力隨[θ]的增大而增大。當[θ]達到一定值時，無滑滾動需要的摩擦力和能提供的最大靜摩擦力相等，此時為無滑滾動和有滑滾動的臨界狀態，此角度為臨界角，記為[θc]，如果[θ>θc]，就會出現滑動，但小球已經具有繞質心轉動的角速度，由定量分析可知該臨界狀態支持力不為零，小球不會立即脫離大球面，還會繼續有滑滾動一段時間。隨著[θ]繼續增大，質心速度[vc]也增大，小球法向合力逐漸增大，而重力的法向分力越來越小，所以支持力會越來越小，當支持力[N]減小到零時，達到最小值，此時小球脫離大球面。

定量計算：大球面的半徑與小球的半徑分別用[R]和[r]（[R>r]）表示。如圖3所示，小球由于偏離大球面的豎直方向的夾角為[θ]，小球滾動轉過的角度為[φ]，小球繞大球面圓心運動的角速度和角加速度分別為[ω1] 和[β1] ，小球繞自身質心（球心）運動的角速度和角加速度分別為[ω2]和[β2]，小球的轉動慣量為

[I=25mr2] ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（4）

小球繞大球面運動，質心的線速度和角速度之間滿足以下關系：

[vc=（R+r）ω1] ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （5）

1.小球做無滑滾動時角速度、角加速度與偏離角度的關系

在開始階段，小球做無滑滾動，設[t=0]時，[θ=0]，[φ=0]，無滑滾動過程中的幾何條件可以寫為：

[R+rθ=rφ] ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （6）

無滑滾動時兩球面接觸位置相對靜止，所以小球的角速度和角加速度滿足以下關系：

[R+rω1=rω2] ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （7）

[R+rβ1=rβ2] ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（8）

以小球為研究對象，由質心運動定律可知，小球運動的滿足方程為：

切線方向：[mgsinθ-f=mR+rβ21]? ? ? ? ? ? （9）

法線方向：[mgcosθ-N=mv2cR+r]? ? ? ? ? ? ? ? ? （10）

由轉動定律可以得到：

[Iβ2=fr]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （11）

由式（4）（8）（9）（11）解得小球質心繞大球面球心轉動的角加速度與偏離角度的關系為：

[β1=57gR+rsinθ]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （12）

又因為小球做無滑滾動時摩擦力為靜摩擦力，摩擦力和支持力都不做功，根據機械能守恒定律可知：

[mgR+r1-cosθ=12mv2c+12Iω22]? ? ? ? ?（13）

由式（4）（5）（7）（13）解得小球質心繞大球面球心轉動的角速度與偏離角度之間的關系為：

[ω1=107gR+r（1-cosθ）]? ? ? ? ? ? ? ? ? ? ? ? ? （14）

式（12）（14）為小球做無滑滾動時質心繞大球面圓心轉動的角加速度和角速度與偏離角度的關系，可以由式（7）（8）得到小球繞自身質心轉動的角速度和角加速度，不再贅述。

2.摩擦因數足夠大時小球脫離大球面的角度以及脫離球面瞬間小球的角速度與線速度關系

由前面分析可知，靜摩擦因數足夠大時小球只能做無滑滾動，小球運動質心的角速度滿足式（14）。另外，小球脫離大球面時大球面對小球的支持力[N=0]，此時的偏離角度為最大偏離角度，記為[θmax]。當[θ=θmax]時，聯立式（5）（7）（10）（14）得到：

[107gR+r（1-cosθmax）=gR+rcosθmax]? ? ? ? ?（15）

所以[cosθmax=1017]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（16）

由式（16）求得為小球脫離大球面時偏離的最大角度[53.97°]。由式（5）求得此時小球運動質心的線速度為[vc=1017R+rg]，繞大球面圓心運動的角速度為[ω1=1017gR+r]，小球繞質心轉動的角速度可以由式（7）求得。

3.摩擦因數為[μ]時，小球做有滑滾動的臨界角

小球做無滑滾動時，摩擦力與壓力之間的關系可以寫為[f=μN']（[N']為壓力），由牛頓第三定律可知小球所受支持力和小球對大球面的壓力是作用力和反作用力，大小相等。小球的動力學方程滿足式（9）和式（10），當[θ=θc]，聯立式（4）（8）（9）（10）（11）（13）（14）可以得到：

[27mgsinθc=17μmg（17cosθc-10）]? ? ? ? ?（17）

結合[sin2θc+cos2θc=1]，余弦函數在[0→90°]是減函數，當[θc]取較小解時已經達到無滑滾動和有滑滾動的臨界狀態， [θc]的較大解就不可能達到臨界狀態，所以解得：

[θc=arccos170μ2+2189μ2+4289μ2+4]（已舍棄較大值） ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （18）

顯然無滑滾動和有滑滾動的臨界角大小和兩個球面接觸的摩擦因數相關。

討論：為了看出臨界角與摩擦因數之間的直觀關系，得出[θc]與[μ]（取[0≤μ≤1]）之間的關系，作出了它們的圖像如圖4（左軸）所示。

由圖4可以看出，[θc]隨[μ]增加而增大。當[μ=0]時，[θc=0°]，即接觸面光滑時，小球一旦偏離平衡位置，只能滑動不會滾動，這時候由于摩擦力為0，小球只受重力和支持力，這兩個力的方向均通過小球質心，產生的力矩為零，根據轉動定理可知小球繞質心轉動的角速度為0，只有純的滑動，沒有轉動。當[μ]足夠大時，[θc=53.97°]，這個角度是小球能夠做無滑滾動的最大角度，由前面的分析可知，這個角度也是小球和大球面脫離的位置。

當小球運動達到無滑滾動和有滑滾動臨界狀態時，由式（10）（19）可以得到，大球面對小球的支持力為：

[N=17mg34189μ2+4-40289μ2+4]? ? ? ? ? ? ? ? ? （19）

作出支持力[N]隨[μ]的變化圖像如圖4（右軸）所示，從圖像上可以看到，支持力隨摩擦因數增大而減小。當[μ]為零時，臨界狀態出現在[θ=0]的位置，此時壓力為[mg]。當摩擦因數足夠大時，臨界狀態的支持力為零，此時的臨界角為最大，也是小球脫離大球面的角度。

從圖4還可以看出，摩擦因數為有限大或有限小時，小球的運動由無滑滾動變為有滑滾動，小球受到的支持力不為零，說明在這個臨界狀態，小球和大球面沒有脫離，小球的偏轉角超過臨界角后，小球還要繼續在大球面上以有滑滾動的形式繼續運動一段時間，只有轉過更大的角度才會和大球面脫離。

三、反思小結

物理習題練習不是簡單地模仿，更重要的是通過對習題進行深層次挖掘，變換題目已知條件，以起到舉一反三的作用。通過對習題的深層次拓展分析，既能豐富學生的知識，又能讓學生深入理解物理題目蘊含的物理規律；既能幫助學生鞏固所學知識，使學生對知識達到融會貫通和觸類旁通的效果，又能有效訓練學生的物理思維，提升學生的解題能力。

［? ?參? ?考? ?文? ?獻? ?］

［1］? 強元棨，程稼夫.物理學大題典：力學［M］.北京：科學出版社，2005.

（責任編輯 黃春香）