基于有限元法的叉車式AGV門架系統結構分析

杜星杰 王飛

摘?要：叉車式AGV作為智能物流工具之一，是未來倉儲物流、智能工廠的重要組成部分。本文以叉車式AGV為研究對象，通過有限元法建立其關鍵結構的分析模型，對其整體結構及關鍵零部件進行靜力學和動力學分析與計算。結果表明，在極限受載狀態下，門架系統各部分的結構強度、變形量及模態分析結果均符合設計要求，為驗證叉車式AGV結構設計的合理性及后續結構優化提供了數據支撐和參考。

關鍵詞：叉車門架；結構分析；有限元法；靜力學；動力學

Abstract：The?forklifttype?Automated?Guided?Vehicle（AGV）is?regarded?as?one?of?the?intelligent?logistics?tools?and?a?crucial?component?in?the?future?of?warehouse?logistics?and?smart?factories.This?study?focuses?on?the?forklifttype?AGV，utilizing?the?finite?element?method?to?establish?an?analytical?model?for?its?key?structures.Both?static?and?dynamic?analyses?and?calculations?were?performed?on?the?overall?structure?and?critical?components.The?results?indicate?that，under?extreme?loading?conditions，the?structural?strength，deformation，and?modal?analysis?of?various?components?of?the?gantry?system?meet?the?design?requirements.This?provides?data?support?and?reference?for?verifying?the?rationality?of?the?forklifttype?AGV's?structural?design?and?subsequent?structural?optimization.

Keywords：Forklift?gantry；structural?analysis；Finite?element?method；statics；dynamics

叉車是一種專門用于搬運、裝卸貨物、堆垛和短途運輸的物料搬運工具［1］，以其易操作、低噪聲、輕巧靈活等優勢，廣泛應用于工廠、倉庫、車站、港口、機場、流通中心等各類場所［23］。近年來，隨著叉車式AGV技術的快速發展和物流行業的高度自動化需求，叉車式AGV（下簡稱“無人叉車”）逐漸成為倉儲物流裝備中不可或缺的一部分。在無人叉車的設計和制造中，叉車門架作為其重要的組成部分之一，主要承擔著叉臂的支撐和操控的重要角色。

叉車門架是叉車中的關鍵部件，通常包括支撐和固定貨叉的框架系統。門架的結構設計將直接影響叉車的穩定性和承載能力。在一般情況下，門架系統由液壓缸、叉架、門架、滾輪以及貨叉等組件構成［4］，這些組件共同協作，使得叉車能夠有效地搬運、裝卸貨物，同時保持平衡和穩定性。由于叉車常常不停歇地工作，叉車門架升降與前后傾動作極為頻繁，其結構設計的合理與否關系到叉車部件運行過程中的應力分布、位移變化等狀況，直接影響叉車門架的工作性能、工作效率和作業的穩定性，進而決定叉車的整體壽命。此外，叉車門架作為主要的承載結構，對多項技術參數都將產生影響，包括額定起重量、載荷中心距、最大起升高度和門架傾角等。因此，深入分析和研究門架的結構特性是提升叉車綜合性能的關鍵［5］。童水光等［6］通過虛擬樣機技術進行叉車的動力學仿真，模擬整個工作過程并生成門架在最危險工況下的載荷文件，然后利用有限元分析技術對叉車門架在這一最危險工況下進行靜力學分析，以觀察門架的應力和應變分布情況，最后針對貨叉根部的應力集中問題，采用多目標數值優化法對貨叉的設計參數進行調整，這一優化過程有助于提高叉車門架的結構穩定性和性能。方文勇等［7］通過FEM有限元分析，比較在不同條件下門架的應力變化情況，以判斷是否需要增強特定部件的強度或者是否需要采取其他操作條件來確保門架的安全使用和壽命。王祖皓等［8］采用各級門架單獨建模和整體建模的方法分別對其進行應力應變分析，然后對門架進行應力應變電測試驗，結合結果進行評估，證明了在有限元分析時，采用整體建模的方法更高效、更可靠。李建萍等［9］通過靜力學分析確定了叉車門架系統在正常工況下的受力狀況，再通過對中橫梁采用不同厚度、折彎半徑和寬度等情況進行有限元分析，最后通過結果分析確定了適宜的中橫梁尺寸，強調應盡可能增大中橫梁的折彎半徑以提高中橫梁的強度。王天等［10］通過Pro/Engineer和ANSYS軟件對叉車門架的有限元強度和剛度進行了分析，并進一步將有限元分析的計算結果與應力測試的試驗值進行了合理性驗證。周京京等［11］采用Solidworks建立了門架系統的實體模型，并通過COSMOSWorks進行了有限元分析，證明在危險條件下，門架的機械特性可以確保叉車的安全操作。Zhuang等［12］針對FEM有限元法分析的準確性不可靠，采用基于MPC184單元模擬方法的有限元法以及獨立分析組件的方法對門架系統進行整體分析。

本文以叉車式AGV為研究對象，采用有限元法對其關鍵部件門架系統進行靜力學和動力學分析與計算，旨在為該類叉車的強度、剛度和振動分析提供仿真數據，同時也為其結構優化提供了數據支撐和參考。

1?門架系統工作原理

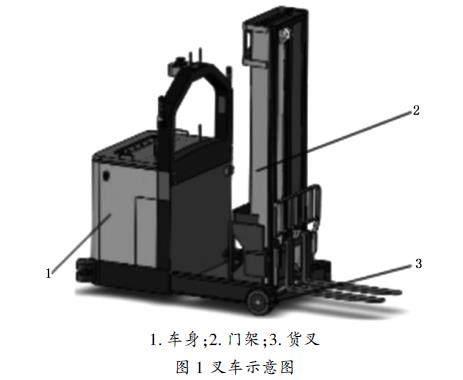
叉車的門架系統主要由貨叉、貨叉架、門架以及起升鏈條組成，如圖1所示。貨叉作為叉車升降貨物的主要部件被安裝在貨叉架上，一般由一對L型的鋼板組成，隨貨叉架上下移動進行裝卸貨物［13］。貨叉架主要用于固定貨叉等其他配件，在液壓油缸和起升鏈條的共同作用下，貨叉架沿門架內的軌道運動。門架是通過橫梁連接而成的門式框架其內側設有豎直軌道，可供貨叉架滑移。起升鏈條為兩條左右對稱分布的片式鏈條，其一端繞過鏈輪與貨叉架底端相連，另一端與門架的上橫梁相連［14］。

門架系統運動狀態可分為兩個階段：在貨叉提升階段，液壓泵將液壓油送入液壓缸，當液壓缸接收到液壓油后，活塞開始向外伸出，驅動鏈輪帶動鏈條，牽動貨叉和貨叉架起升。在貨叉下降階段，液壓缸內的液壓油通過閥門回流至油箱，液壓缸的活塞則會緩慢返回，從而實現貨叉的下降［1516］。

2?門架結構有限元分析

通過對叉車門架結構進行有限元分析能模擬和評估門架在各種負載和工作條件下的行為，包括強度、剛度、振動特性以及疲勞壽命，可幫助深入了解叉車的結構性能，用于預測結構在不同工況下的響應，確保門架在長期使用中的安全性和可靠性。

2.1?模型建立

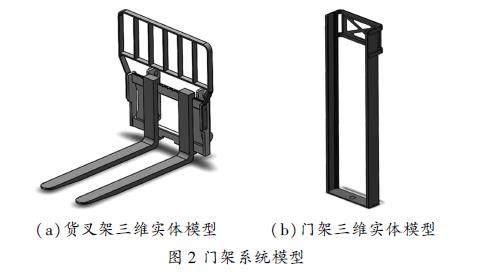
門架系統包含零件眾多，為了提高計算效率，在保證計算精度的前提下對模型進行一些簡化。本文以某型號平衡重式無人叉車為例進行分析，采用三維建模軟件建立了門架的簡化幾何模型，只保留門架主體結構主要部分，簡化了一些小型連接件等不重要的次要細節。如圖2所示，簡化后的模型由貨叉架和門架組成。

2.2?材料屬性

貨叉架和門架結構材料選用65Mn，詳細特性參數如表1所示。

2.3?門架結構靜力學分析

靜力學分析采用節點—位移模型，將幾何模型離散化，單元位移和節點位移間的關系表達式如下：

{u}=［N］{δ}e（1）

其中：{u}為單元內部任意一點的位移列陣，［N］為形函數矩陣，{δ}e為節點位移矩陣。由式（1）可導出單元應變與節點位移的關系：

{ε}=［B］{δ}e（2）

其中{ε}為單元內部任意一點的應變列陣，［B］為單元應變矩陣。

根據本構方程，單元應力和節點的位移關系為：

{σ}=［D］{ε}=［D］［B］{δ}e（3）

其中{σ}為單元內任意一點的應力列陣，［D］為單元彈性矩陣，與材料相關。

根據變分原理，建立單元節點力和節點位移的平衡方程，并導出單元的剛度矩陣：

{f}e=［K］e{δ}e（4）

［K］e=∫BT［D］［B］dv（5）

其中{f}e為單元載荷列陣，［K］e為單元剛度矩陣。

將各單元剛度矩陣組合可得總體結構平衡方程：

{f}=［K］{δ}（6）

其中，{f}為總體載荷列陣，［k］為總體剛度矩陣。

將邊界條件和載荷代入式（6）可求得各節點處的位移，再根據式（2）和式（3）可求得各單元處的應變和應力。

對整個門架系統進行靜力分析以研究叉車在極端工作條件下的數據。當貨叉架提升至最大高度時，對門架的底部和背部施加固定約束，對兩個貨叉架分別施加9800N的壓力，以模擬貨叉均勻受載2噸的情況。

P=FA=9800113653.87=0.086MPa（7）

在網格劃分時進行網格靈敏度分析，當網格尺寸為5mm時，網格數量約為220萬，此時網格質量為0.88；當網格尺寸為10mm時，網格數量為22.6萬，此時網格質量為0873。因此為了節約計算成本，將網格尺寸設定為10mm，劃分的網格模型如圖3所示。分析計算得到門架系統滿載下等效應力圖及結構變形圖（如圖4、圖5所示）。

由圖4所示，在貨叉表面均布載荷的作用下，貨叉的應力主要集中在貨叉折彎處，表現為拉應力，應力由折彎處向兩側遞減。門架系統的最大應力發生在貨叉根部，大小為102.12MPa，小于65Mn的屈服極限（785MPa），變化量均在彈性范圍內的變形，不會出現塑性變形。在載荷作用下，貨叉根部出現應力集中現象，有可能發生疲勞斷裂。根據計算貨叉安全系數為7.69，大于設計安全系數3.0。因此，貨叉符合設計要求。由圖5所示，在額定載荷作用下，貨叉變形量由叉尖向根部減小。最大變形值位于貨叉尖端，為13.23mm，校核其剛度：

13.23mm＜l50=96050=19.2mm（8）

式中l為貨叉長度。從分析可知，貨叉剛度在許用范圍內，但是變形量較大，可以進行優化設計。

2.4?門架結構動力學分析

叉車式AGV在實際工作不僅會受到貨物靜載荷，還會受到隨時間變化的動載荷。門架系統和叉車前橋連接，為了防止叉車工作中發生共振，對車身和門架系統進行振動分析是十分必要的。

常用模態分析微分方程為：

Mx¨+Cx·+Kx=ft（9）

式中：［M］為質量矩陣，［C］為阻尼矩陣，［K］為剛度矩陣，x¨為加速度矩陣，x·為速度矩陣，x為位移矩陣，f（t）為外激勵矩陣，這里為零矩陣。根據叉車結構及各部件之間連接關系，設定阻尼剛度矩陣為零。多自由度無阻尼振動系統微分方程可表示為：

Mx¨+Kx=0（10）

綜合考慮門架系統振動和路面激勵帶來的影響，選取前六階作為頻率提取范圍。對門架進行前六階模態分析，獲得門架前六階自由模態頻率和振型，分別如表2門架前六階振動頻率和圖6門架前六階振型圖所示。

如圖6所示，門架不僅呈現純彎曲振動，還表現出繞其中心旋轉的振動。在前六個振型中，純彎曲振型占據主導地位，對門架的影響最為顯著。這些振動形式都會對門架立柱結構的剛度和強度產生影響。因此，在實際工程設計中，可以通過合理布置門架的質量、增加橫梁數量、調整橫梁布置位置等方法，有效降低振動對門架的不良影響。

一般情況下，路面激勵的頻率屬于較低的范圍，即時間頻率在0.5～20Hz之間。通過對門架的前六個固有頻率進行分析，發現門架的第一階固有頻率為29.846Hz，超出了常規的激勵頻率范圍。這符合設計要求，意味著叉車在工作過程中門架不太可能發生共振現象。

門架由于底部固定在叉車前橋上，且重心位置極少發生變化，所以，剛度較大，產生的振動較輕。門架與車的振動頻率不相等，因此不會產生共振現象，滿足設計要求。

結語

本文以叉車式AGV為研究對象，運用靜力學和動力學分析對叉車門架系統進行了研究，并采用有限元法對門架結構進行了仿真分析，結果表明，在靜力學分析中，門架和貨叉的強度剛度均符合設計要求，但貨叉的變形量較大，需要進一步優化；在動力學分析中，門架與車身將不會發生共振，確保了無人叉車的運行平穩性。上述仿真結果為驗證叉車門架的強度、剛度和振動頻率提供了依據，同時也為門架系統的結構優化提供了數據支撐和參考。

參考文獻：

［1］張義壯，馮川.電動叉車舉升機構設計及有限元分析［J］.機械研究與應用，2020，33（03）：4851.

［2］趙子文，張其豐，呂巖軍.叉車門架剛度有限元分析［J］.現代制造技術與裝備，2022，58（02）：15.

［3］齊善朋，岳君.基于ANSYS的叉車外門架結構有限元分析［J］.科技創新與應用，2014（29）：61.

［4］陳利杰.叉車門架結構的改進與優化［J］.科技與企業，2016（04）：164.

［5］相曙鋒.叉車門架強度分析與結構改進［J］.工程機械，2022，53（04）：2326+8.

［6］童水光，何順，童哲銘，等.叉車門架動靜態聯合仿真及多目標優化［J］.機械設計，2018，35（12）：711.

［7］方文勇.FEM在叉車門架重疊度更改中的應用［J］.機械工程與自動化，2017（05）：8990.

［8］王祖皓，尹輝俊，張蕓華，等.某叉車門架有限元模型評估［J］.廣西科技大學學報，2015，26（04）：2125.

［9］李建萍，李澤陽，許金棟，等.叉車外門架中橫梁的受力及有限元分析［J］.工程機械，2013，44（11）：4650+3.

［10］王天，韓振.3t平衡重式叉車門架有限元分析［J］.工程機械，2012，43（12）：2427+7.

［11］周京京，穆希輝，馬振書，等.全向側面叉車門架有限元分析及運動仿真［J］.起重運輸機械，2009（02）：6568.

［12］Zhuang?Y，Shan?D?Z，Zhang?Q.Finite?Element?Analysis?of?a?Forklift?Truck?Mast?System［J］.Applied?Mechanics?and?Materials，2014，2963（494495）：668672.

［13］姚鍇，袁曉金，段志梅，等.叉車門架裝置類型的探討［J］.機電工程技術，2022，51（02）：189191.

［14］丁亮.叉車起升系統設計思路的探討［J］.物流技術與應用，2021，26（05）：151153.

作者簡介：杜星杰（1988—?），男，漢族，內蒙古烏蘭察布市涼城縣人，本科，技師，研究方向：車輛工程。