數(shù)學(xué)軟件引入概率統(tǒng)計(jì)課堂教學(xué)的探索與實(shí)踐

寧桂英

（柳州工學(xué)院，廣西柳州 545616）

工業(yè)革命4.0 引發(fā)的快速變革，對(duì)高校人才培養(yǎng)提出了新的要求，在此背景下，新工科建設(shè)成為我國(guó)新時(shí)期高等教育改革的指導(dǎo)方針[1]。新工科的實(shí)質(zhì)是培養(yǎng)具備較強(qiáng)的工程實(shí)踐能力、創(chuàng)新能力，能夠滿足行業(yè)發(fā)展需求的應(yīng)用型和技能型人才[2]。大學(xué)數(shù)學(xué)作為本科院校的一門重要的公共基礎(chǔ)課程，傳統(tǒng)教學(xué)模式已不能滿足新工科需求，因此，許多學(xué)者已嘗試進(jìn)行改革[3-11]。

概率論與數(shù)理統(tǒng)計(jì)是研究隨機(jī)現(xiàn)象統(tǒng)計(jì)規(guī)律的一門數(shù)學(xué)學(xué)科，具有廣泛的應(yīng)用性，被應(yīng)用于工程技術(shù)、經(jīng)濟(jì)管理和預(yù)測(cè)、科學(xué)研究、企業(yè)管理等眾多領(lǐng)域[12]，且其理論和方法對(duì)解決許多實(shí)際問(wèn)題有著重要的作用。但由于該課程內(nèi)容深?yuàn)W抽象、公式繁多且計(jì)算復(fù)雜，傳統(tǒng)的課堂教學(xué)難以達(dá)到學(xué)生用所學(xué)知識(shí)解決實(shí)際問(wèn)題能力的培養(yǎng)。為了更好地滿足新工科對(duì)人才的需求，有必要對(duì)概率統(tǒng)計(jì)課程進(jìn)行教學(xué)改革。本文結(jié)合柳州工學(xué)院教學(xué)實(shí)際，探討了將數(shù)學(xué)軟件引入概率統(tǒng)計(jì)課堂，在激發(fā)學(xué)生學(xué)習(xí)興趣的同時(shí)，培養(yǎng)學(xué)生動(dòng)手能力和解決問(wèn)題能力，進(jìn)而提高課堂教學(xué)質(zhì)量。

1 概率統(tǒng)計(jì)課程教學(xué)現(xiàn)狀

概率論與數(shù)理統(tǒng)計(jì)是柳州工學(xué)院大學(xué)二年級(jí)理工科專業(yè)學(xué)生的一門重要的公共數(shù)學(xué)基礎(chǔ)課，共48學(xué)時(shí)，為解決課時(shí)少、內(nèi)容多、學(xué)生知識(shí)面拓寬受限等問(wèn)題，采用了線上線下混合教學(xué)模式，在一定程度上提高了課堂效率，但由于沒(méi)有單獨(dú)開(kāi)設(shè)數(shù)學(xué)實(shí)驗(yàn)課程，數(shù)學(xué)軟件在課堂教學(xué)中的應(yīng)用有限，難以很好地在課堂上動(dòng)態(tài)呈現(xiàn)隨機(jī)現(xiàn)象的變化規(guī)律，對(duì)一些復(fù)雜計(jì)算問(wèn)題也只停留在依靠板書推導(dǎo)的過(guò)程，缺乏用數(shù)學(xué)軟件進(jìn)行演示性操作和解決具體問(wèn)題的實(shí)踐操作，在一定程度上限制了學(xué)生的思維，難以調(diào)動(dòng)學(xué)生學(xué)習(xí)的積極性。

2 數(shù)學(xué)軟件引入概率統(tǒng)計(jì)課堂的探索

隨著教育技術(shù)的現(xiàn)代化和計(jì)算機(jī)軟件的快速發(fā)展，計(jì)算機(jī)作為多媒體教學(xué)的輔助工具，已廣泛應(yīng)用于各類課堂。目前已開(kāi)發(fā)出各種非常有效的統(tǒng)計(jì)軟件，在概率統(tǒng)計(jì)課堂教學(xué)中有針對(duì)性地引入這些數(shù)學(xué)軟件，一方面，可以幫助師生從煩瑣的計(jì)算中解脫出來(lái)，更好地觀察、理解、掌握基本理論和方法，調(diào)動(dòng)學(xué)生學(xué)習(xí)的積極性，提高教師課堂教學(xué)效率；另一方面，教師在案例分析中通過(guò)數(shù)學(xué)軟件引導(dǎo)學(xué)生進(jìn)行數(shù)學(xué)建模，在實(shí)踐中培養(yǎng)和提高學(xué)生發(fā)現(xiàn)問(wèn)題、分析問(wèn)題和解決實(shí)際問(wèn)題的能力，幫助學(xué)生建立用數(shù)學(xué)建模方法解決實(shí)際問(wèn)題的意識(shí)，學(xué)生有了實(shí)踐的機(jī)會(huì)，學(xué)習(xí)興趣顯著提高。已有學(xué)者研究了在大學(xué)數(shù)學(xué)課程中引入平板電腦的優(yōu)勢(shì)[13]。

3 數(shù)學(xué)軟件引入概率統(tǒng)計(jì)課堂的實(shí)踐

3.1 利用數(shù)學(xué)軟件對(duì)隨機(jī)現(xiàn)象進(jìn)行直觀演示和解釋

法國(guó)數(shù)學(xué)家拉普拉斯曾說(shuō)：“生活中最重要的問(wèn)題，絕大多數(shù)在實(shí)質(zhì)上都是概率問(wèn)題”[14]。誠(chéng)然，概率論與數(shù)理統(tǒng)計(jì)課程中很多概念與公式的產(chǎn)生都源于解決生活中的問(wèn)題，這些概念與公式的數(shù)學(xué)語(yǔ)言描述都很抽象，單一理論講解，學(xué)生難以理解，若用Excel 或Matlab 軟件進(jìn)行模擬演示，可以幫助學(xué)生更好地理解公式和概念，從而更好地運(yùn)用概念解決問(wèn)題，彌補(bǔ)了傳統(tǒng)課堂教學(xué)的不足。

如：在講頻率時(shí)，頻率具有穩(wěn)定性，隨著實(shí)驗(yàn)次數(shù)的增加，頻率會(huì)穩(wěn)定在某具體數(shù)值附近，按照傳統(tǒng)的教學(xué)法學(xué)生難以理解。但如果教師在課堂上動(dòng)態(tài)演示拋硬幣實(shí)驗(yàn)，通過(guò)現(xiàn)場(chǎng)實(shí)驗(yàn)直觀觀察這一穩(wěn)定性，學(xué)生就能深刻理解隨著實(shí)驗(yàn)次數(shù)的增加，頻率穩(wěn)定于某一具體數(shù)值的過(guò)程，為后續(xù)對(duì)概率定義的理解做好鋪墊。圖1 是用Matlab 模擬拋硬幣100 次、1 000 次和10 000 次的過(guò)程中，動(dòng)態(tài)演示硬幣正面和反面出現(xiàn)次數(shù)的過(guò)程。

圖1 拋硬幣實(shí)驗(yàn)

中心極限定理是概率論與數(shù)理統(tǒng)計(jì)中一個(gè)非常重要的定理，也是比較難以理解的內(nèi)容之一，在實(shí)際問(wèn)題中，許多隨機(jī)現(xiàn)象都是由大量相互獨(dú)立的隨機(jī)因素綜合影響而形成的，其中每個(gè)因素所起作用又都是微小的，這類隨機(jī)變量都服從或近似服從正態(tài)分布。而中心極限定理指出：無(wú)論隨機(jī)變量服從什么分布，n個(gè)隨機(jī)變量和的極限分布一定是服從正態(tài)分布的。定理內(nèi)容很抽象，可以用Matlab 分別演示離散型0～1 分布和的分布與連續(xù)型均勻分布和的分布情況（見(jiàn)圖2），引導(dǎo)學(xué)生觀察，隨機(jī)變量個(gè)數(shù)越多，和的分布就越接近正態(tài)分布，學(xué)生通過(guò)動(dòng)態(tài)觀察后，更易理解定理的內(nèi)容。

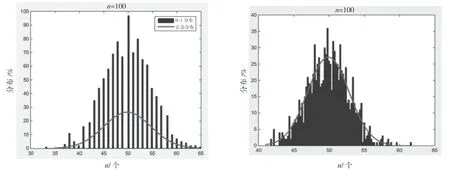
圖2 隨機(jī)變量的個(gè)數(shù)n 越大，和的分布越近似于正態(tài)分布

為使學(xué)生加深對(duì)中心極限定理的理解，可用該定理解釋身邊的現(xiàn)象，如：在賭博游戲里，莊家常常在兩邊放置值錢的東西吸引顧客，這種游戲可信嗎？以高爾頓釘板實(shí)驗(yàn)為例，用Matlab 動(dòng)態(tài)演示，如圖3 所示，在演示的過(guò)程中可以看出，小球落在中間的概率遠(yuǎn)遠(yuǎn)大于落在兩邊的概率，即小球落入小槽的個(gè)數(shù)是呈正態(tài)分布的，這也就揭穿這個(gè)游戲的奧秘。通過(guò)計(jì)算機(jī)演示，解釋了生活現(xiàn)象，達(dá)到學(xué)以致用的目的。

圖3 高爾頓實(shí)驗(yàn)

3.2 設(shè)置應(yīng)用型案例，強(qiáng)化軟件應(yīng)用，培養(yǎng)數(shù)學(xué)建模能力，增強(qiáng)教學(xué)內(nèi)容的實(shí)效性

概率論與數(shù)理統(tǒng)計(jì)是研究隨機(jī)現(xiàn)象的一門學(xué)科，在生活中有著廣泛的應(yīng)用。教學(xué)中挖掘概率知識(shí)在生活中的應(yīng)用案例，一方面，增強(qiáng)學(xué)生學(xué)習(xí)的積極性，拓展知識(shí)面；另一方面，通過(guò)對(duì)實(shí)際問(wèn)題的求解，培養(yǎng)學(xué)生數(shù)學(xué)建模能力和軟件應(yīng)用能力，進(jìn)而提高學(xué)生的高階思維能力，為學(xué)生后續(xù)的學(xué)習(xí)、工作奠定基礎(chǔ)。

全概率公式和貝葉斯公式是概率論部分的重點(diǎn)和難點(diǎn)內(nèi)容，公式抽象復(fù)雜，學(xué)生難以理解公式內(nèi)涵。在教學(xué)中，教師用案例教學(xué)法，以“海難空難”搜救案例引入，并將概念及其應(yīng)用融入案例中。如：以美軍“天蝎號(hào)”核潛艇搜救為例，圖4 為以Matlab模擬“天蝎號(hào)”搜救過(guò)程。

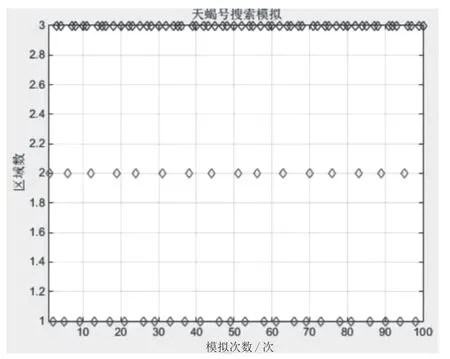
圖4 Matlab 模擬“天蝎號(hào)”搜救過(guò)程

首先將實(shí)際問(wèn)題數(shù)學(xué)化，簡(jiǎn)化為如下數(shù)學(xué)問(wèn)題：

設(shè)“天蝎號(hào)”核潛艇沉沒(méi)在甲、乙、丙3 個(gè)區(qū)域之一，潛艇技術(shù)部門判斷其概率分別為1/2，1/3，1/6；搜救專家搜索這些地域，若有核潛艇，發(fā)現(xiàn)的概率分別為1/2，2/3，1/4；如果搜索甲區(qū)域后未找到核潛艇，“天蝎號(hào)”沉沒(méi)于甲區(qū)域的概率是多少？

先從簡(jiǎn)單問(wèn)題入手，設(shè)A=“搜索甲區(qū)域未找到核潛艇”，B1，B2，B3分別表示核潛艇沉沒(méi)在甲、乙、丙三個(gè)區(qū)域，則

貝葉斯公式：P(B1|A)=P(AB1)/P(A)=P(B1)P(A|B1)/P(A)=1/3

接著教師引領(lǐng)學(xué)生深入探討，在第一輪搜索后，“天蝎號(hào)”最可能沉沒(méi)在哪個(gè)區(qū)域？啟發(fā)學(xué)生用貝葉斯公式判斷，在引導(dǎo)學(xué)生進(jìn)行了兩輪的計(jì)算后，學(xué)生基本掌握了貝葉斯方法的迭代過(guò)程，理解了貝葉斯公式的原理，此時(shí)進(jìn)一步提問(wèn)：“天蝎號(hào)”最終是如果找到的？是這樣一直用手工計(jì)算下去嗎？有沒(méi)有簡(jiǎn)單的方法呢？面對(duì)這個(gè)復(fù)雜的實(shí)際問(wèn)題，學(xué)生也很想知道用什么方法計(jì)算簡(jiǎn)單。此時(shí)啟發(fā)學(xué)生可以用計(jì)算機(jī)計(jì)算，鼓勵(lì)學(xué)生動(dòng)手操作，通過(guò)計(jì)算機(jī)動(dòng)態(tài)模擬搜救過(guò)程，能快速實(shí)現(xiàn)在200 次的搜索中展示搜索區(qū)域的變化情況，即形象生動(dòng)，又展示了計(jì)算機(jī)計(jì)算的高效性，這種理實(shí)結(jié)合的教學(xué)方式，使學(xué)生在知識(shí)學(xué)習(xí)的過(guò)程中也掌握了獲取知識(shí)的方法，學(xué)生學(xué)習(xí)興趣高漲。學(xué)生課后反饋：不僅輕松掌握了貝葉斯公式，而且了解了貝葉斯公式的具體應(yīng)用，更重要的是了解了以數(shù)學(xué)建模方法解決實(shí)際問(wèn)題的基本思想，記憶深刻。

3.3 借助數(shù)學(xué)軟件，實(shí)現(xiàn)復(fù)雜的數(shù)學(xué)計(jì)算

概率論與數(shù)理統(tǒng)計(jì)的教學(xué)目標(biāo)之一是使學(xué)生能夠熟悉數(shù)據(jù)處理、數(shù)據(jù)分析、數(shù)據(jù)推斷的基本方法，并能用所掌握的方法分析和解決實(shí)際問(wèn)題。在大數(shù)據(jù)時(shí)代，信息資源越來(lái)越豐富，在用數(shù)理統(tǒng)計(jì)知識(shí)處理實(shí)際問(wèn)題時(shí)面對(duì)的數(shù)據(jù)量也越來(lái)越龐大，需要借助計(jì)算機(jī)軟件來(lái)計(jì)算。在Matlab 的統(tǒng)計(jì)工具箱中，提供了常見(jiàn)的樣本求解函數(shù)，操作簡(jiǎn)單，容易實(shí)現(xiàn)，如樣本均值、樣本方差的計(jì)算，點(diǎn)估計(jì)的計(jì)算等。教師在數(shù)理統(tǒng)計(jì)部分的教學(xué)中適當(dāng)介紹Matlab 的應(yīng)用，可簡(jiǎn)化樣本處理的計(jì)算過(guò)程，增加課堂活力，拓寬學(xué)生眼界，提高課堂教學(xué)效率，同時(shí)也為學(xué)生進(jìn)一步利用軟件處理大數(shù)據(jù)能力的培養(yǎng)奠定基礎(chǔ)。

在求解樣本均值時(shí)，調(diào)用mean 函數(shù)，直接返回樣本平均值；調(diào)用var 函數(shù)，返回樣本無(wú)偏估計(jì)的方差；調(diào)用mle（‘norm’,x,0.05）格式，返回正態(tài)分布的置信水平為95%的置信區(qū)間；調(diào)用ztest 函數(shù)，可實(shí)現(xiàn)在方差已知情況下對(duì)總體均值的檢驗(yàn)，而在方差未知時(shí)可調(diào)用ttest 函數(shù)對(duì)均值進(jìn)行假設(shè)檢驗(yàn)等，實(shí)踐證明：正確運(yùn)用Matlab 軟件，不僅可避免繁瑣的計(jì)算，而且調(diào)動(dòng)了學(xué)生學(xué)習(xí)的積極性，學(xué)生也有動(dòng)手實(shí)踐的機(jī)會(huì)，增加了數(shù)學(xué)課堂的趣味性。

3.4 數(shù)學(xué)軟件引入教學(xué)，促進(jìn)學(xué)生核心素養(yǎng)的培養(yǎng)

數(shù)學(xué)軟件的引入，提高了課堂效率，在此情況下組織課堂教學(xué)內(nèi)容、設(shè)置教學(xué)案例、設(shè)計(jì)教學(xué)活動(dòng)等都對(duì)教師提出了更高的要求。教學(xué)內(nèi)容的組織安排、教學(xué)案例的挑選、教學(xué)活動(dòng)的設(shè)計(jì)旨在促進(jìn)學(xué)生核心素養(yǎng)的培養(yǎng)，為學(xué)生后續(xù)的學(xué)習(xí)和發(fā)展奠定堅(jiān)實(shí)的基礎(chǔ)。數(shù)學(xué)建模是根據(jù)實(shí)際問(wèn)題來(lái)建立數(shù)學(xué)模型，然后利用軟件對(duì)數(shù)學(xué)模型進(jìn)行求解，最后根據(jù)計(jì)算結(jié)果解決實(shí)際問(wèn)題。因此，將數(shù)學(xué)建模思想引入課堂，通過(guò)設(shè)置解決實(shí)際問(wèn)題的教學(xué)案例，引導(dǎo)學(xué)生用所學(xué)知識(shí)分析、建模，并用數(shù)學(xué)軟件求解，不僅實(shí)現(xiàn)了教學(xué)模式和教學(xué)方法的創(chuàng)新，而且使學(xué)生學(xué)會(huì)了主動(dòng)思考和動(dòng)手實(shí)踐，在這個(gè)過(guò)程中，學(xué)生的創(chuàng)新精神和創(chuàng)新能力都得到了培養(yǎng)，邏輯思維能力和軟件應(yīng)用能力也得到鍛煉和提升，真正實(shí)現(xiàn)了以學(xué)生為主體的教學(xué)理念。同時(shí)在教學(xué)中，深入挖掘數(shù)學(xué)概念、教學(xué)案例中的課程思政元素，使學(xué)生在學(xué)習(xí)數(shù)學(xué)知識(shí)的同時(shí)得到思想的啟發(fā)和教育，可促進(jìn)學(xué)生核心素養(yǎng)的培養(yǎng)，教學(xué)效果顯著。

4 數(shù)學(xué)軟件引入概率論與數(shù)理統(tǒng)計(jì)課程的實(shí)踐效果

筆者將數(shù)學(xué)軟件引入概率論與數(shù)理統(tǒng)計(jì)課堂教學(xué)，通過(guò)近兩年的教學(xué)實(shí)踐，學(xué)生反饋：提高了數(shù)學(xué)興趣，被數(shù)學(xué)的魅力吸引，增強(qiáng)了數(shù)學(xué)建模解決實(shí)際問(wèn)題的意識(shí)，提高了動(dòng)手能力和軟件應(yīng)用能力。相對(duì)于傳統(tǒng)課堂教學(xué)，學(xué)生學(xué)習(xí)興趣提升，課外學(xué)習(xí)情況明顯好轉(zhuǎn)，課堂教學(xué)質(zhì)量明顯提高。學(xué)生分析問(wèn)題、解決問(wèn)題的能力得到提升，在各級(jí)各類數(shù)學(xué)建模競(jìng)賽中多次打破紀(jì)錄，創(chuàng)造佳績(jī)。這些充分證明將數(shù)學(xué)軟件引入概率統(tǒng)計(jì)課堂，能夠順應(yīng)新時(shí)代教育教學(xué)要求，符合學(xué)生發(fā)展需求，值得推廣。

5 結(jié)束語(yǔ)

本文以在新工科背景下高校人才培養(yǎng)目標(biāo)為出發(fā)點(diǎn)，改革教學(xué)內(nèi)容、教學(xué)模式和教學(xué)方法，強(qiáng)化統(tǒng)計(jì)思想和方法的理解，突出知識(shí)的運(yùn)用，這些改革措施依托數(shù)學(xué)軟件的引入來(lái)實(shí)現(xiàn)。將數(shù)學(xué)軟件引入概率論與數(shù)理統(tǒng)計(jì)課程的教學(xué)，能夠簡(jiǎn)化煩瑣的手工計(jì)算，實(shí)現(xiàn)了理論教學(xué)與實(shí)踐教學(xué)的有機(jī)結(jié)合，實(shí)踐證明：改革后的教學(xué)方法新穎，教學(xué)內(nèi)容更加直觀清晰，易于理解，課堂教學(xué)效率高。教無(wú)定法，需要因材施教，要想達(dá)到滿意的效果，需要教師認(rèn)真鉆研教學(xué)素材，精心組織教學(xué)，從人才培養(yǎng)角度考慮，將數(shù)學(xué)軟件引入課堂是教學(xué)改革的趨勢(shì)，值得廣大數(shù)學(xué)教學(xué)工作者探索和思考。