中國上市企業的損失厭惡：行為特征與驅動因素

魏彥杰，鐘 娟

（安徽財經大學 國際經濟貿易學院，安徽 蚌埠 233030）

0 引言

企業面對不確定時的風險抉擇行為一直是經濟學領域的熱點問題。由于企業未來的經營狀態存在不確定性，因此他們需要依據自身對不確定性的感知及風險厭惡程度，在回報和風險之間作出選擇。不過，現實中的企業常常表現出相互矛盾的風險偏好[1]，個體決策的“前景理論”[2]將這種兼具風險追求和風險厭惡的雙重特征歸結為企業面對不確定性時的損失厭惡，即厭惡損失而非厭惡風險。企業的風險決策事實上取決于回報與目標之差[3]：當回報低于目標值時，企業表現出風險追求；相反，當回報高于目標值時，企業表現出風險厭惡。即在目標值（拐點）兩側，企業在回報和風險之間的選擇截然不同，形成一種非線性的“U”型關系[4]。這種“U”型關系反映了企業面對不確定時的羊群行為，即企業僅追求一個尚可的目標績效，這是企業經營上的惰性行為，它背離了企業家精神，降低了微觀主體效率。

雖然前景理論整體解釋了企業決策中回報和風險承擔之間的因果機制，但關于中國企業的損失厭惡行為卻一直缺乏系統性討論[5]：（1）研究者往往更關注拐點左側的風險追求行為以及這種冒險傾向的后果及其治理，卻很少關注損失厭惡行為的整個曲線形態及其驅動力；（2）研究者也并未關注“U”型曲線非對稱性的形成過程；（3）損失厭惡行為的特點在于它同時包含拐點左側的風險追求行為與拐點右側的風險厭惡行為，但目前研究者很少關注企業內外部因素對風險追求與風險厭惡的不同作用。

前景理論將企業視為激進與惰性、冒險與保守的組合體，因此更全面地觀察企業的損失厭惡行為特征和驅動因素，對激發企業家精神、幫助企業更合理地應對外部不確定性風險，以及建設世界一流企業具有重要意義。基于此，本文使用2000—2019年中國上市企業財務數據，針對損失厭惡行為的非線性整體特征、分位數特征和分樣本特征三個方面，以及分行業的異質性進行分析，細致觀察企業行為決策中“回報-風險”因果機制的非線性關系，以便全景式地展現中國企業面對不確定性時的“回報-風險”抉擇行為，為企業行為研究提供來自中國的經驗證據。

1 研究設計

1.1 變量選取

1.1.1 被解釋變量與解釋變量

被解釋變量：企業風險承擔（SDrebit）。本文使用盈余波動性來度量企業風險承擔水平，它反映了管理者在資源配置中的風險決策所帶來的企業收入不確定性。具體測度性方法如下：首先，計算企業當年息稅前利潤率與當年該企業所處行業平均盈余回報率的差值；其次，以每三年（t-1 年至t+1 年）為一個觀測時段①采用其他年份滾動方法，如t 年至t+2 年的數據來測度企業盈余波動性并不改變本文的主要結果。，計算該差值的標準差；最后，為避免解釋變量回歸系數過小，將得到的標準差乘以100②這種處理并不影響回歸系數的正負和顯著性水平，只是將回歸系數放大了100倍，以避免回歸系數過小難以表示的問題。。其中，測度過程中使用的行業劃分標準為證監會《上市公司行業分類指引》（2012年版）。

解釋變量：企業回報（rebit）。與企業風險承擔的測度方法相對應，本文選取息稅前利潤率來代表企業回報水平。

1.1.2 控制變量

（1）企業經營層面變量：①資產負債率（Lev）：企業總負債除以總資產。一般認為，資產負債率越高的企業（杠桿水平更高），其風險承擔水平也越高，因此預期Lev的系數為正。②企業規模（Size），企業總資產的對數。企業規模也是決定風險承擔水平的重要因素，相對于大企業，小企業具有更強烈的風險偏好，其風險承擔水平更高，因此預期Size系數為負。③企業成長性（Grow），營業收入增長率。營業收入增長越快的企業，其經營狀況越好，盈利能力也越強，企業通過高風險經營方式獲取利潤的動機則越弱，因此預期Grow系數為負。④創新效率（InnoEff），計算方法為Patent/ln(1+研發支出)，其中，Patent的計算方法為企業發明、實用新型和外觀設計三種專利的年度總申請量加1 后的自然對數，3 種專利按3∶2∶1 設置權重。InnoEff反映了每單位研發投入的專利申請數，InnoEff越高，創新產出能力越強。（2）企業特質層面變量：企業年齡（Age），計算方法為觀測年份減去公司成立年份。（3）公司治理層面變量：獨立董事比例（Idp），計算方法為獨立董事人數除以董事會總人數。（4）企業外在環境變量：行業內市場集中度（HHI）。首先，本文將各細分行業合并為20個行業大類；然后，設某細分行業l下的公司i在年份t的營業收入為ORl，i，t，其市場占有率為MSl，i，t=ORl，i，t/∑ORl，t，則該行業l的HHI為HHIl，t=∑(MSl，i，t)2；最后，設某行業大類L下的公司數量為lnum，其包含的每個細分行業公司數目為lnum，并以此為權重，得到每個行業大類L的HHI為HHIL，t=∑(lnum/lnum)HHIl，t。HHI越小，表明行業內競爭越激烈，反之亦然。

1.2 研究方法

1.2.1 損失厭惡行為的非線性模型

按照前景理論的假設，若企業存在損失厭惡行為，則其回報水平與風險承擔水平之間具有“U”型的非線性關系。因此，使用半參數固定效應回歸方法來驗證這一假設，同時指定企業回報rebit為進入模型的非線性連續變量，并設定如下模型：

其中，i和t分別表示公司和年份。

1.2.2 損失厭惡行為的分位數回歸模型

為了進一步從企業風險承擔水平的角度觀察企業損失厭惡行為，本文使用其分位數來考察不同風險承擔水平下企業損失厭惡程度的變化情況。計量方法使用廣義分位數回歸[6]，計量模型中同時包含變量rebit的一次項和二次項，模型表述式如下：

分位數q包括0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、0.99，并按照各分位數下SDrebit的均值，使用Fisher 最優分割法將其劃分為三種類型，即低風險（q≤0.5）、中風險（0.5＜q≤0.8）、高風險（q＞0.8）。

按照二次函數的定義，本文重點觀察兩個指標：（1）二次函數曲線的開口方向和陡峭程度，即β2。若β2＞0，則曲線開口向上，為“U”型曲線；| |β2越大，二次函數曲線開口越小，曲線越陡峭。（2）二次函數曲線拐點的橫坐標，即-β1/2β2。按照前景理論，該數值代表了“U”型曲線的拐點值。

1.2.3 損失厭惡行為的分樣本回歸模型

為了進一步厘清曲線左側風險追求行為和右側風險厭惡行為的細節，特別是他們在驅動因素上的差異，使用“U”型曲線拐點將總樣本分割為風險追求和風險厭惡兩個子樣本，分別記為Srs 和Sra。

第一步，為保證拐點值估計盡可能準確，本文單獨對rebit進行擬合，并同時考慮時間、個體和行業效應，設定如下模型：

由此得到拐點值為0.0691（即息稅前利潤率為6.91%）。

第二步，按照0.0691 的拐點值，將rebit＜0.0691 的數據點定義為Srs，rebit≥0.0691的數據點定義為Sra。并使用如下模型分別估計兩個子樣本：

在模型（4）中，各控制變量被作為調節變量，與rebit分別構成交叉項。本文使用控制函數法處理內生性問題，先針對rebit使用工具變量法生成殘差項res，再在模型回歸中加入殘差項res作為解釋變量。

工具變量選擇如下：在Srs 下為中國貿易政策不確定性指數TPU和滯后一期的融資約束指數（kz）（kz的計算方法參照文獻[7]）；在Sra 下為企業年度發明專利授予量Patent.Award（發明專利授予量加1后取自然對數）、監事與董事比例（RSD）、中國經濟政策不確定性指數（EPU）、中國貿易政策不確定性指數（TPU）、PPP調整后全球經濟不確定性指數（GEPU）。EPU、TPU、GEPU數據均來源于www.policyuncertainty.com。

1.3 數據來源

初始樣本為2000—2019 年中國滬深A 股上市企業，數據來自國泰安（CSMAR）數據庫，并進行以下處理：（1）剔除金融業上市企業；（2）對息稅前利潤率、資產負債率、營業收入增長率進行1%和99%的縮尾處理，以消除異常值的影響；（3）剔除樣本數據少于3 年的企業和企業數小于2家的行業，并據此計算2000—2019年每家企業的風險承擔水平。最終獲得3254 家上市企業的30315 個非平衡面板數據。

2 實證分析

2.1 損失厭惡行為的整體特征

對模型（1）使用Phillips-Perron 方法的Fisher PP 檢驗結果顯示，P值均在5%的水平上拒絕原假設，所有變量均平穩。模型回歸結果見圖1和表1。

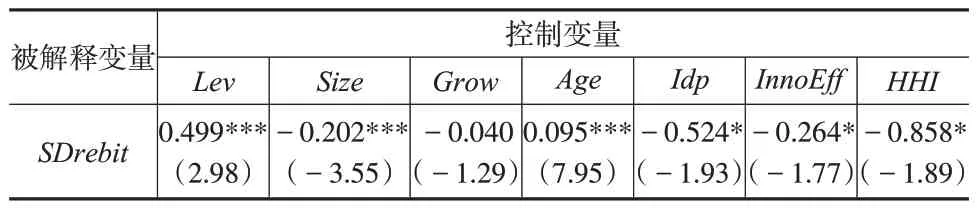
表1 半參數模型中控制變量回歸結果

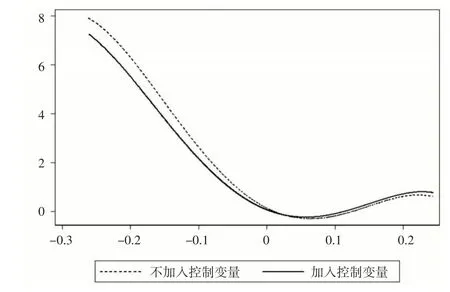
圖1 半參數模型中非線性變量rebit 的回歸結果

圖1 報告了企業回報rebit的平均非參數擬合結果，本文同時比較了不加入和加入控制變量兩種情況。（1）擬合結果符合前景理論的假設（圖1中黑色實線），企業回報rebit與其風險承擔SDrebit之間具有非對稱“U”型關系。（2）即使不加入控制變量，“U”型曲線形態也初步完備（見圖1 中黑色虛線），這說明損失厭惡行為主要受到回報水平的影響。（3）加入控制變量后，“U”型曲線拐點左側斜率明顯降低，右側變化則不明顯。這可能是因為控制變量影響企業風險承擔水平，且這一影響在拐點左右兩側對rebit與SDrebit的關系產生了不同的間接作用，進而差異化地影響了“U”型曲線形態，本文在后文使用調節效應驗證了這一假設。

從表1 中各類控制變量的回歸結果看：資產負債率Lev對SDrebit具有顯著正向作用，企業規模Size則具有顯著負向作用，資產負債率越低、規模越大的企業，其風險承擔水平也越低。企業年齡Age具有顯著正向作用，企業年齡越大，其風險承擔水平越高。獨立董事比例Idp具有顯著負向作用，獨立董事的風控功能抑制了企業風險承擔。創新效率InnoEff具有顯著負向作用，提升創新效率有助于緩解企業風險承擔。行業內市場集中度HHI具有顯著負向作用，行業內競爭越激烈，企業風險承擔水平越高。不過，企業成長性Grow沒有表現出顯著作用。

2.2 損失厭惡行為的分位數特征

依據模型（2）的設定，本文在不同分位數下重點觀察了二次函數曲線的開口方向和陡峭程度β2以及二次函數曲線拐點的橫坐標-β1/2β2的動態變化，結果見圖2。

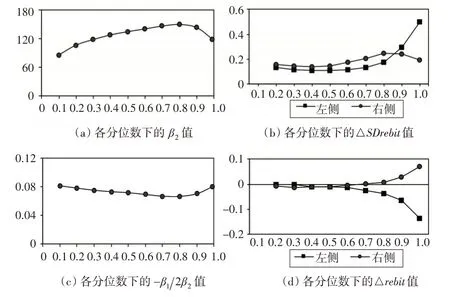
圖2 不同風險承擔水平分位數下二次函數曲線的形態特征

2.2.1 “U”型曲線形態的變化

（1）圖2（a）顯示，模型（2）中β2＞0，符合損失厭惡“U”型曲線特征。在中低風險區間（0.1～0.8 分位數），隨著企業風險承擔水平增加，β2值持續增加，“U”型曲線變得陡峭，損失厭惡行為增強。在0.8 以上的高風險區間，β2值轉而降低，損失厭惡程度略有下降，“U”型曲線曲率變小。

（2）為進一步揭示“U”型曲線曲率變化的動態過程，本文計算了SDrebit各分位數下拐點值兩側數據點的風險承擔均值，并設其邊際值為ΔSDrebit（見圖2（b））。可以發現，在0.8 分位數及以下的中低風險區間，拐點兩側ΔSDrebit呈現一致性的緩慢上升趨勢，風險追求與風險厭惡行為同步增長。但在0.8 分位數以上的高風險區間，拐點右側的ΔSDrebit快速下降，風險厭惡行為減弱，左側ΔSDrebit則快速上升，風險追求行為急劇增強。由此可見，損失厭惡程度在0.8 分位數后下降主要受到拐點右側風險厭惡程度降低的影響，“U”型曲線變平緩。

2.2.2 “U”型曲線拐點值的變化

（1）圖2（c）顯示，在中低風險區間（0.1～0.8 分位數），隨著β2值不斷增加，拐點值-β1/2β2也不斷減小，為回避風險增加和盡可能擠進羊群，企業愿意接受更低的心理目標回報，保守程度增強。但在0.8 分位數以上的高風險區間，隨著風險繼續增加，拐點值-β1/2β2轉而上升，該范圍內新增了風險水平最高的19.9%數據點，他們反而具有激進的回報與風險抉擇特征，追求高風險、高回報。

（2）為了進一步揭示拐點值動態變化的根源，本文計算了SDrebit各分位數下拐點兩側數據點的回報水平均值，并設其邊際值為Δrebit（見圖2（d））。可以發現，在0.8分位數及以下的中低風險區間，拐點兩側Δrebit值非常接近，且在0 值上下波動，索取風險回報的行為均不強烈。但在0.8 分位數以上的高風險區間，拐點右側的Δrebit快速上升（回報水平均值從0.106上升到0.118），回報對風險的補償增強，增長的回報降低了風險壓力，風險厭惡減弱，曲線右側變緩；而左側Δrebit則快速下降（回報水平均值從0.038 下降到0.031 下），回報對風險的補償降低，風險壓力增大，風險追求增強，曲線左側變陡。由此可見，拐點值在0.8分位數后轉而開始上升主要是受到拐點右側新增數據點對高風險索取額外回報的影響。

總體來看，圖2中需要特別關注那些在0.8 分位數以上新增的數據點，他們在“U”型曲線動態形成過程中扮演關鍵角色，是曲線非對稱性的主要驅動力。與處在0.8 分位數及以下中低風險區間的企業不同，在0.8分位數以上，處于拐點左側的企業具有快速增長的風險、快速降低的風險回報以及由此引發的強烈風險追求；而處在拐點右側的企業也承受著高風險，并具有索取額外風險回報的激進行為，其風險厭惡程度也更低。從某種意義上講，他們更像是同一類企業，其風險偏好都極易引發冒險性的經營行為。因此，“U”型曲線的非對稱性歸因于不同風險承擔水平下風險追求與風險厭惡行為的非對稱性。

2.3 區分風險追求行為與風險厭惡行為的分樣本特征

依據模型（3）得到的“U”型曲線拐點值，本文將總樣本分割為風險追求和風險厭惡兩個子樣本，分別記為Srs 和Sra，并使用模型4 進行估計，結果見表2。表2 結果顯示：在Sra 子樣本下，加入交叉項后調節變量發生了較大變化（見列（5）至列（8）），這種共線性問題在調節效應分析中比較常見。因此，在Sra 子樣本下，調節變量解讀應以列（5）和列（7）為準，調節效應解讀以列（6）和列（8）為準。

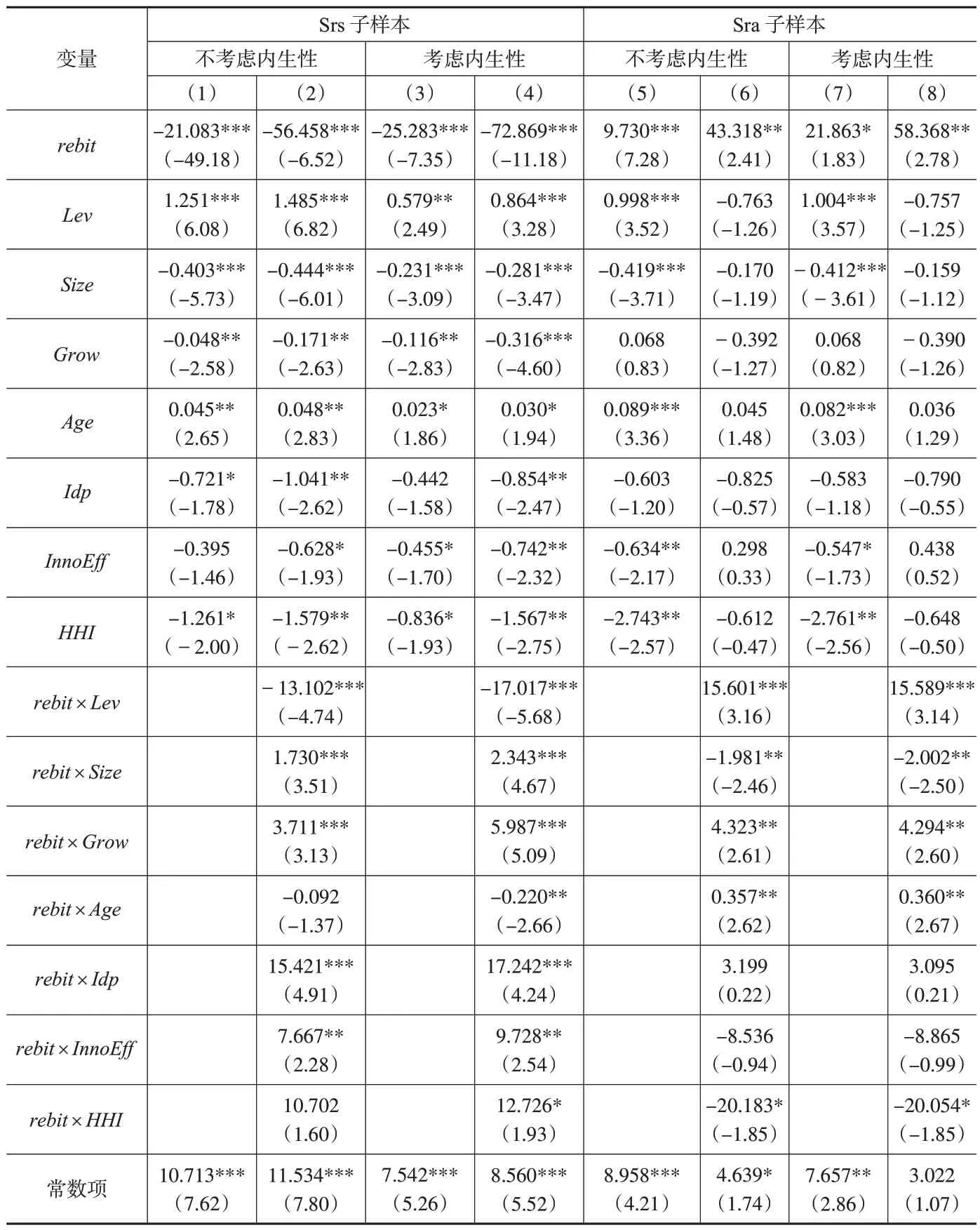
表2 區分風險追求與風險厭惡的分樣本回歸結果

第一，從主效應的回歸結果看，企業回報水平對企業風險承擔的影響符合損失厭惡行為特征。在Srs 子樣本中，企業回報rebit與企業風險承擔SDrebit顯著負相關，拐點左側存在風險追求行為。在Sra 子樣本中，rebit與SDrebit顯著正相關，拐點右側存在風險厭惡行為。

第二，從調節效應回歸結果看，各控制變量在拐點兩側表現出不同的調節作用。在Srs 子樣本中，主效應rebit顯著為負。調節變量Size、Grow、Idp、InnoEff、HHI的系數均顯著為負，且其交叉項rebit×Size、rebit×Grow、rebit×Idp、rebit×InnoEff、rebit×HHI的系數均顯著為正，表明這5 個調節變量在影響風險追求行為中與rebit具有替代關系，并對降低企業風險追求具有關鍵作用。調節變量Lev、Age的系數顯著為正，且其交叉項rebit×Lev、rebit×Age的系數顯著為負，表明這兩個調節變量強化了rebit對SDrebit的負向影響，企業資產負債率越高、企業年齡越大，其風險追求行為越強烈。在Sra 子樣本中，主效應rebit的系數顯著為正。交叉項rebit×Grow的系數顯著為正，顯示高營業收入增長率加劇了企業的風險厭惡。調節變量Lev、Age的系數顯著為正，且其交叉項rebit×Lev和rebit×Age的系數也顯著為正，更高的資產負債率和企業年齡會助長風險厭惡行為。調節變量Size和HHI的系數顯著為負，且其交叉項rebit×Size和rebit×HHI的系數也顯著為負，表明Size和HHI弱化了rebit對SDrebit的正向影響，企業規模越大以及其所處行業集中度越高（競爭越弱），企業的風險厭惡程度越低。交叉項rebit×Idp和rebit×InnoEff沒有顯著作用，與拐點左側的情況不同，獨立董事比例和創新效率與風險厭惡行為沒有顯著關系。

第三，各控制變量的調節效應在拐點兩側存在強度差異。比較列（4）和列（8）中交叉項系數的絕對值可以發現：（1）資產負債率加劇風險追求的作用更強，拐點左側低回報企業對負債壓力更敏感。（2）與資產負債率的情況相反，企業年齡和行業內市場集中度更易加劇風險厭惡。高齡企業出現強風險厭惡的可能性更高，高回報企業比低回報企業對市場競爭更敏感。（3）企業規模對風險追求的抑制作用更強，規模增長更有利于低回報企業減少冒險行為而非激勵高回報企業增加風險承擔。（4）企業成長性在拐點兩側有不同作用，但其抑制風險追求的作用強于其加劇風險厭惡的作用。（5）獨立董事比例和創新效率則是僅對拐點左側風險追求行為具有抑制作用的調節變量，他們減弱了低回報企業的激進冒險程度。

總之，這些調節變量對風險追求與風險厭惡行為施加了不同影響，如表3所示。

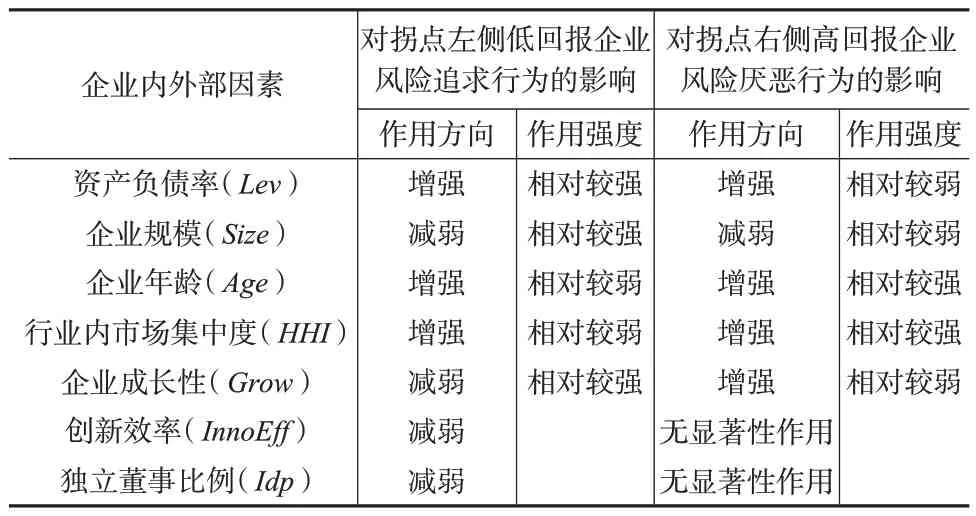
表3 企業內外部因素對風險追求與風險厭惡行為的調節效應差異

3 穩健性檢驗

3.1 放寬樣條平滑中的級數

為檢驗“回報-風險”函數的“U”型關系的可靠性，本文放寬樣條平滑中的級數。一般來說，采用不超過5階的級數已足夠精確擬合任何形式的多項式函數[8]。因此，針對模型（1）分別使用6階、7階的級數設置，見圖3。

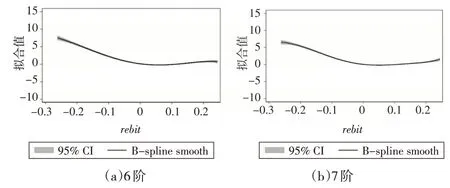
圖3 模型（1）使用6階、7階級數的估計結果比較

圖3 顯示，雖然本文放寬樣條平滑中的級數到6 階、7階，但各級數間曲線形態變化很小，“回報-風險”函數關系非常穩健，企業回報與其風險承擔之間確實存在著前景理論所推斷的損失厭惡“U”型曲線關系。

3.2 替換被解釋變量與擴大樣本范圍

為檢驗企業損失厭惡行為的可靠性，本文使用擴大樣本范圍并替換被解釋變量的方法對“回報-風險”的“U”型曲線再次進行驗證。（1）使用企業營業利潤率（opr）來測度SDopr。（2）改變Winsor方法，在原始數據中按照3σ原則重新對息稅前利潤率和營業利潤率進行0.27%和99.73%縮尾處理。結果見圖4。

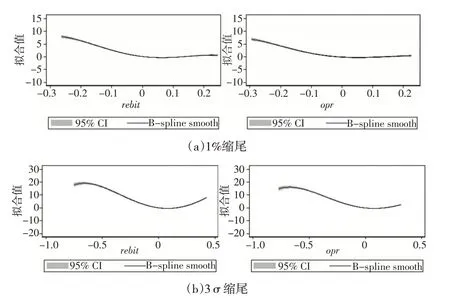
圖4 兩種縮尾處理方法下rebit 和opr 非參數擬合結果比較

圖4 結果顯示：（1）在1%縮尾處理下，使用營業利潤率opr替換rebit后的擬合結果與圖1 非常相似。（2）在擴大樣本的3σ縮尾處理下，“回報-風險”函數的非對稱“U”型曲線關系依然成立。（3）由于3σ縮尾增加了更多rebit和opr極高和極低的數據點，按照前景理論的觀點，企業盈余水平越低，風險追求傾向越強烈；盈余水平越高，風險厭惡傾向越強烈，因此3σ縮尾下的“U”型曲線比1%縮尾下的更為陡峭。（4）opr擬合結果的曲線較rebit的更為平緩。這說明中國企業對息稅前利潤率比營業利潤率更敏感，對上市公司而言，努力維持一個尚可的息稅前盈余水平，是自己仍在羊群中的重要標志。

3.3 替換解釋變量

本文針對模型（4），替換其解釋變量，以檢驗其穩定性。（1）企業創新。使用創新投入（Rd）和創新產出（Patent）來代替創新效率（InnoEff），其中，Rd的計算方法為公司年度研發支出占總資產的比重，Patent的計算方法為發明、實用新型和外觀設計三種專利的總申請量加1后的自然對數①此處使用的創新產出指標與計算創新效率時使用的創新產出指標稍有不同，3種專利沒有進行加權處理。。（2）公司治理。使用直接控股股東持股比例（Ssr）替代獨立董事比例（Idp）。更高的股權集中度意味著控制人對企業具有更強的控制力和更高的利益相關性，這可能會促使控制人選擇更為穩健的經營方式，以保證其私有收益。結果見下頁表4。

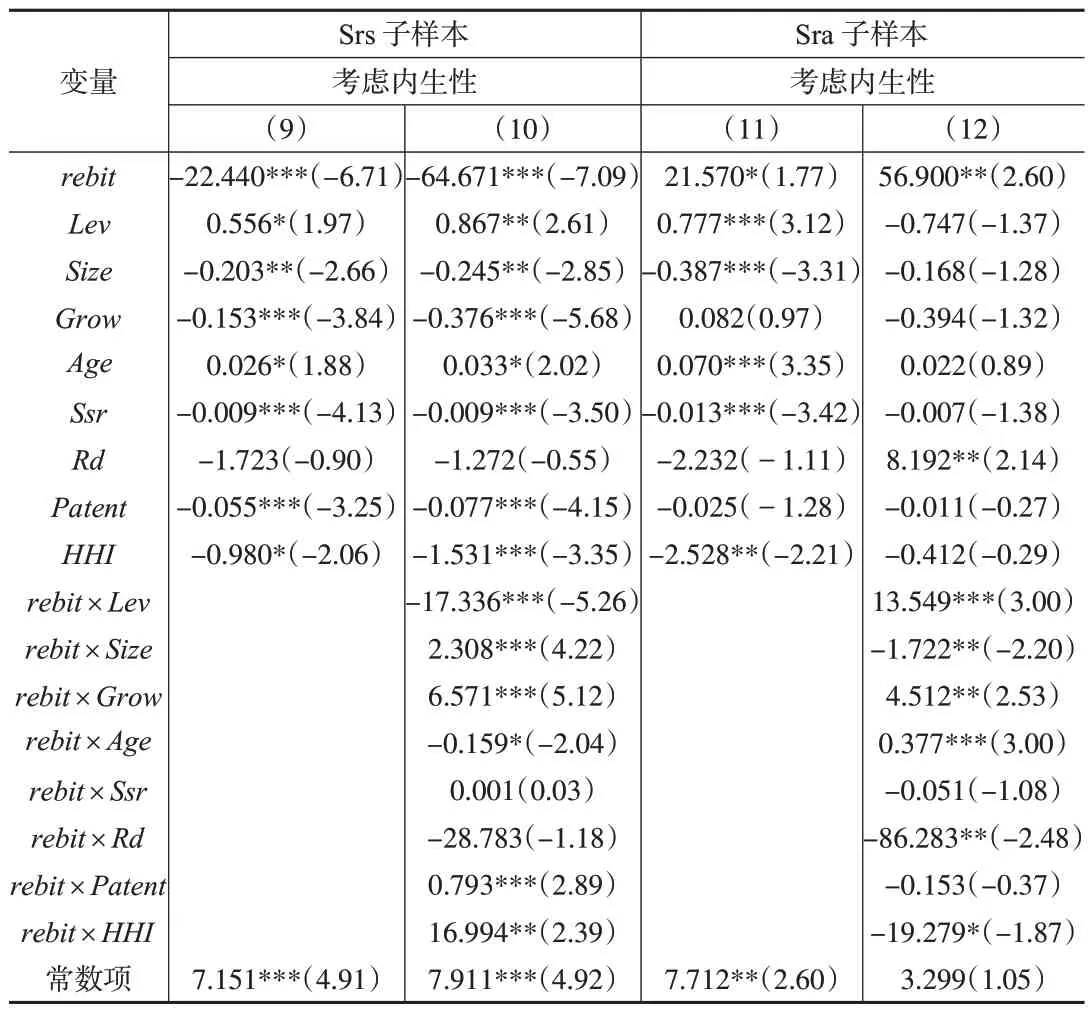
表4 替換解釋變量的穩健性檢驗

與表2 相比，替換解釋變量后的回歸結果差異很小。但從列（10）、列（12）可以看出，在拐點兩側的調節效應都不顯著，更高的股權集中度并不具有獨立董事制度所特有的風控功能。此外，創新投入（Rd）與創新效率（InnoEff）的調節作用不同，Rd對企業風險追求行為沒有顯著影響，但對風險厭惡有助長作用，這說明Rd對高回報企業具有明顯的成本壓力，強化了其風險厭惡。

4 分行業的異質性分析

本文嘗試從上市公司行業特征差異的角度對損失厭惡行為進行探討，按照20個行業大類，分別使用模型（3）得到企業回報rebit的平均非參數擬合結果。回歸結果顯示：在20 個行業大類中，對非參數部分rebit的擬合結果整體符合“回報-風險”函數的非對稱“U”型關系。但曲線形態在行業間差異較大。雖然多數行業均呈現左側略陡峭、右側略平緩的特征，但部分行業也表現出左側很陡峭但右側很平緩（醫藥；房地產業）、兩側差異很小（電力燃氣及水的生產和供應業等）、右側反而比左側更陡峭（建筑業）、右側呈現負斜率（農林牧漁業）等比較特殊的“回報-風險”函數關系。

本文推測，各行業間“回報-風險”“U”型曲線的差異可能緣于各行業競爭程度的差別。因為：（1）當行業內競爭激烈時，預期回報低于目標回報的概率將增加，企業在拐點左側的風險追求傾向增強，“U”型曲線左側變得陡峭。（2）當行業內競爭激烈時，在拐點右側存在兩種可能。第一種，如果競爭導致預期回報超越目標回報的難度增大，企業在拐點右側的風險厭惡程度將增強，曲線右側將變得陡峭；第二種，如果競爭引發強烈的競優行為，企業在拐點右側的風險厭惡程度將降低，曲線右側反而變得平緩。（3）同理，當行業內競爭弱化時，一方面，回報不達標概率將降低，曲線左側變得平緩；另一方面，壟斷水平提升增加了獲取壟斷利潤的可能性，曲線右側將變得平緩。

為驗證這一推斷，本文使用Fisher最優分割法將20個行業大類的HHI區分為高低兩類。同時，將每一行業大類的總樣本分為rebit小于拐點值的子樣本S.rebit 和大于等于拐點值的子樣本L.rebit，并分別對rebit和SDrebit進行線性回歸，得到每一行業大類在拐點左右兩側的rebit回歸值，并與該行業大類的市場集中度進行比較，如圖5所示。圖5 中高HHI 和低HHI 行業均按HHI 值降序排列，所得結果支持了前文的推斷。

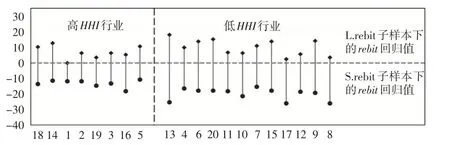
圖5 高HHI行業、低HHI行業“U”型曲線拐點兩側斜率比較

5 結論

本文實證考察了2000—2019 年中國上市企業的損失厭惡行為特征與驅動因素，結果表明：（1）中國上市企業存在損失厭惡行為，其主因來自企業回報水平的變化，且回報水平與風險承擔水平之間具有非對稱的“U”型關系。（2）“U”型曲線的非對稱性歸因于不同風險承擔水平下風險追求與風險厭惡行為的非對稱性。（3）企業內外部的其他因素也會影響“U”型曲線的形態，并對風險追求與風險厭惡行為施加不同影響。