一種基于AK-MCS-K的失效概率函數估計方法

宋海征 周長聰 李磊 林華剛 岳珠峰

摘要：

針對可靠性優化設計中失效概率函數求解復雜、計算量大等問題，提出一種求解失效概率函數的高效方法。所提方法的基本思路是利用自主學習Kriging方法構造輸入變量全空間在失效邊界處的局部代理模型，進而通過該局部代理模型結合Monte Carlo模擬法計算在指定分布參數樣本下結構的失效概率，然后基于Kriging方法擬合分布參數樣本點與對應結構失效概率之間的函數關系，最終建立用Kriging模型表達的失效概率函數的隱式函數。為了檢驗所提方法的精度和效率，給出了兩個算例，對比了所提方法與已有的求解失效概率函數方法的計算結果。算例結果表明，所提方法適用于求解復雜的功能函數問題，并在滿足精度要求的基礎上顯著降低了計算量。

關鍵詞：結構可靠性；失效概率函數；自主學習Kriging方法；代理模型

中圖分類號：TB114.3

DOI：10.3969/j.issn.1004132X.2024.05.003

開放科學（資源服務）標識碼（OSID）：

An Estimation Method of Failure Probability Function Based on AK-MCS-K

SONG Haizheng1，2? ZHOU Changcong1，2? LI Lei1，2? LIN Huagang1，2? YUE Zhufeng1，2

1.School of Mechanics，Civil Engineering and Architecture，Northwestern Polytechnical University，

Xian，710072

2.State Key Laboratory of Clean and Efficient Turbomachinery Power Equipment，

Northwestern Polytechnical University，Xian，710072

Abstract： An efficient method for solving the failure probability function was proposed to address the difficulties of solving the failure probability function in reliability optimization design， such as complexity and large amount of computation. The basic idea of the proposed method was to utilize the adaptive Kriging method to construct a local surrogate model of the full space of input variables at the failure boundary. The local surrogate model was then combined with the Monte Carlo simulation method to calculate the failure probability of the structures under the specified distribution parameter samples. The functional relationship between the sample points of the distribution parameters and the structural failure probability was then fitted by the Kriging method. Finalization of the implicit function of the failure probability function expressed in terms of the Kriging model. In order to test the accuracy and efficiency of the proposed method， two examples were given to compare the computational results of the proposed method with those of the existing methods for solving failure probability functions. The results of examples show that the proposed method is suitable for solving complicated functional function problems and significantly reduces the amount of computation while satisfying the accuracy requirements.

Key words： structural reliability; failure probability function; adaptive Kriging method; surrogate model

收稿日期：20231229

基金項目：航空科學基金（20220015053005） ，陜西省自然科學基金（2021JQ-072）

0? 引言

工程實際中往往存在著大量由于加工制造誤差、外部載荷差異以及人為因素而導致的結構的不確定性，基于可靠性的優化設計逐漸成為一種有效的分析手段［1-2］。工程中，一般輸入隨機變量的分布形式是已知的，但其分布參數通常是未知的。結構失效概率與分布參數之間的函數關系式被稱為失效概率函數［3-5］。在可靠性優化設計中，通常需要計算結構在不同分布參數下的結構失效概率值。求得結構失效概率函數后，可將結構可靠性優化問題轉化為一般確定性優化問題，從而顯著提高優化的效率［6-8］。

然而，失效概率函數的求解是非常不易的。最直接的策略是在不同的分布參數值下進行多次可靠性分析，得到逐點的失效概率，該方法被稱為雙循環Monte Carlo模擬（double-loop Monte Carlo simulation，DLMCS）法［3］。然而，在復雜的工程背景下，DLMCS需要重復多次對功能函數進行評估，其計算量往往是不能接受的，一般將DLMCS法計算結果作為測試其他新方法的參考。AU［9］提出了一種單循環Monte Carlo模擬（single-loop Monte Carlo simulation，SLMCS）法，基于貝葉斯規則和擴展可靠性思想，將失效概率函數的求解轉化為擴展失效概率和分布參數的條件聯合概率密度函數的求解問題，提高了失效概率函數的求解效率。CHING等［10］對AU［9］提出的方法進行了擴展，核心思想是利用最大熵原理估計設計參數的后驗分布，進而估計失效概率函數。YUAN［4］提出了一種“加權方法”，其基本思想是用一次可靠性分析中所產生樣本的顯示函數表示為失效概率函數。SONG等［11］提出了一種基于一次線抽樣信息就能得到失效概率函數的局部近似方法。此外，基于代理模型的方法也被用于失效概率函數的估計，該類方法的基本思想是在設計參數空間中選擇一些預定義的插值點，并利用代理模型構建近似值，從而逼近失效概率函數［12］。KAYMAZ［13］提出采用Kriging法、支持向量機法等去逼近失效概率函數。JENSEN［14］提出采用線性多項式逼近失效概率函數的對數，并進一步求解失效概率函數。LING等［3］基于貝葉斯規則和擴展可靠性理論提出一種自主學習Kriging結合Monte Carlo模擬（MCS）法估計失效概率函數的方法。

一種基于AK-MCS-K的失效概率函數估計方法——宋海征? 周長聰? 李? 磊等

中國機械工程 第35卷 第5期 2024年5月

為了解決已有方法存在的計算量較大、計算效率低下及計算精度較差等問題，本文提出了一種基于自主學習Kriging結合Monte Carlo模擬法和Kriging（adaptive Kriging and Monte Carlo simulation and Kriging， AK-MCS-K）的失效概率函數估計法。該方法首先在輸入變量全空間內通過自主學習Kriging方法構造靠近失效域邊界處的局部Kriging模型，然后將該模型作為功能函數的粗略估計并結合Monte Carlo 模擬法計算分布參數樣本點的結構失效概率，最后利用Kriging法擬合分布參數樣本點與結構失效概率之間的函數關系，此時將得到的Kriging模型視為失效概率函數的隱式表達。

1? 失效概率函數

1.1? 失效概率函數的表達

在工程設計問題中，假定某結構的功能函數為Y=g（X），其n維輸入變量表示為X=（X1，X2，…，Xn）T，通常輸入變量的分布形式已知，但是其分布參數（如均值和方差）需要設計。假設n維輸入變量的分布參數為θ=（θ1，θ2，…，θd）T（d為分布參數的個數），考慮θ為不確定性變量。當分布參數θ固定時，其條件聯合概率密度函數為fX（x|θ）（x為當分布參數θ取固定值時的樣本，每個樣本均有多維元素），結構的失效域定義為F={x∶g（x）≤0}，此時系統的失效概率可表示為

Pf（θ）=P（F|θ）=∫…∫RnIF（x）fX（x|θ）dx（1）

其中，IF（x）表示失效域內指示函數，當x∈F時，IF（x）=1，否則IF（x）=0。可以看到，結構的失效概率隨著分布參數θ的變化而變化，也即失效概率可看作分布參數θ的函數，此時Pf（θ）被認為是失效概率函數。

以失效概率為約束條件的優化問題可以表示為

min f（θ）

s.t.Pfi{gi（θ）≤0}≤P*fi? ?i=1，2，…，p1

hj（θ）≤0j=1，2，…，p2

gk（θ）=0k=1，2，…，p3

θL≤θ≤θUθ∈Rn（2）

式（2）被稱為可靠性優化問題。其中，θ為未知的分布參數向量（即優化模型中的設計變量）；f（θ）表示目標函數；Pfi為第i個失效概率約束，P*fi為第i個失效概率閾值；p1為失效概率約束的個數；hj、gk分別為確定性的不等式約束和等式約束；p2、p3分別為不等式約束和等式約束的個數；θL、θU分別為θ的下限和上限。如果在優化前求得結構的失效概率函數Pf（θ），則上述可靠性優化問題可以轉化為一般的確定性優化問題，這無疑可以顯著提高優化的效率。

1.2? 失效概率函數的求解

1.2.1? DLMCS法

雙循環Monte Carlo模擬（DLMCS）法是求解失效概率函數最直接的方法，其基本思想是：首先將輸入變量的分布參數離散化，然后針對每個分布參數樣本點求解對應的失效概率，最后利用插值法求解結構的失效概率函數。求解步驟如下：

（1）在分布參數空間中抽取N個分布參數樣本。

（2）針對每個樣本點θi（i=1，2，…，N），根據其條件概率密度函數fX（x|θi）生成M個輸入變量樣本（x（i）1，x（i）2，…，x（i）M）T，其中，θi為分布參數θ的一組固定值。

（3）計算M個輸入變量的功能函數值g（x（i）j）（i=1，2，…，N;j=1，2，…，M）。

（4）計算逐點的失效概率函數估計值，其表達式如下：

P^f（θi）=1M∑Mj=1IF（x（i）j）（3）

利用DLMCS法只是得到了失效概率函數在某些分布參數樣本點處的離散值，并不是顯示的失效概率函數表達式。該方法計算失效概率函數的計算量為NDLMCS=N×M。在實際工程應用中，DLMCS法的計算量很大，往往難以接受，但其計算結果準確，通常用作檢驗其他新方法的標準解。

1.2.2? SLMCS法

單循環Monte Carlo模擬（SLMCS）法的出現是為了解決DLMCS法計算量過大的問題的。基于貝葉斯規則，SLMCS法將失效概率函數Pf（θ）轉換成如下式所示：

Pf（θ）=Pθ（θ|F（x，θ））×P{F（x，θ）}fΘ（θ）（4）

其中，F（x，θ）表示當x和θ同時為隨機變量時組成的空間（x，θ）上的失效域；fΘ（θ）表示分布參數的聯合概率密度函數；Pθ（θ|F（x，θ））表示分布參數θ的條件概率密度函數；P{F（x，θ）}表示當x和θ同時為隨機變量時的擴展失效概率，可由下式表示為

P{F（x，θ）}=∫F（x，θ）fX（x|θ）dxdθ（5）

由式（4）可知，通過求得Pθ（θ|F（x，θ））和P{F（x，θ）}后，很容易得到失效概率函數Pf（θ）。基于貝葉斯規則和擴展可靠性思想，求解失效概率函數Pf（θ）的計算量僅存在于計算擴展失效概率P{F（x，θ）}中，因此SLMCS法能夠顯著降低失效概率函數求解時的計算量。但在工程實際中，SLMCS法仍然需要多次調用功能函數以保證擴展失效概率P{F（x，θ）}的準確性，在復雜工程問題上，其計算量依然很難接受。

針對SLMCS方法計算量依然較大的問題，采用自主學習Kriging結合Monte Carlo模擬法（AK-MCS）對其進行了改進。AK-MCS法通過采用自主學習Kriging法構造一個收斂的Kriging模型，替代SLMCS法中分布參數的離散過程，減少擴展失效概率的計算量，并最終降低了失效概率函數求解時的計算量。由于構造Kriging模型所需要的樣本點數目遠小于樣本池中樣本的數目，因此AK-MCS方法的高效性可以得到保證。

2? 基于AK-MCS-K的失效概率函數估計

2.1? 基本原理

本文提出了一種基于AK-MCS-K方法估計失效概率函數的新方法。利用Monte Carlo模擬法構造分布參數的大容量樣本池S（θ），針對S（θ）中每個分布參數樣本進行抽樣，進而構造輸入變量的全空間樣本池S。在諸多代理模型中，Kriging模型是一種估計方差最小的無偏估計模型，具有全局近似與局部隨機誤差相結合的特點，因此本文利用樣本池S中的部分樣本構造收斂的Kriging模型。Kriging近似表達為多項式與高斯過程之和，其表達式如下：

gk（X）=pT（X）β+z（X）（6）

其中，gk（X）表示未知的Kriging模型；pT（X）為回歸函數向量；β為未知系數向量；z（X）表示高斯過程，其均值為零，協方差為

Cov（z（xi），z（xj））=σ2R［R（xi，xj）］（7）

其中，σ2為過程方差；R為相關矩陣；R（xi，xj）表示任意兩個樣本點的相關函數，i，j=1，2，…，m，m為訓練樣本點個數，其中高斯函數為常用的相關函數，如下式所示：

R（xi，xj）=∏nk=1exp（－θk（x（k）i－x（k）j）2）（8）

其中，n為輸入變量的維數；θk（k=1，2，…n）為未知的相關參數；x（k）i、x（k）j分別為xi和xj的第k個元素。

超參數{β，σ2，θ}的估計表示為{β^，σ^2，θ^}，可通過最大似然估計獲得，因此對于全空間樣本池S中的每一個樣本x，其均值和方差分別由下式計算：

g^k（x）=pT（x）β^+rT（x）R－1（g－Pβ^）（9）

σgk（x）=σ^2［1－rT（x）R－1r（x）+（r（x）R－1P－

p（x））T（PTR－1P）－1（r（x）R－1P－p（x））］（10）

rT（x）=（R（x，x1），R（x，x2），…，R（x，xm））T

其中，rT（x）為x與訓練樣本點之間的相關函數向量；g為訓練樣本點的響應值組成的列向量；P為單位列向量。

相對于其他代理模型，Kriging法一個顯著的優勢是在給出預測值的同時能夠給出預測的方差，因此本文建立了一種自主學習的Kriging模型。首先通過少量的訓練樣本集訓練粗糙的模型，然后將剩余樣本作為候選樣本集，通過自主學習函數選擇候選樣本集中符合要求的樣本點加入到訓練樣本集中，最后更新Kriging模型，直到模型精度達到要求。

失效概率的計算過程中，判斷極限狀態函數的正負極為重要。準確計算失效概率的關鍵是利用代理模型精確逼近失效面，即g（x）=0。本文的自主學習Kriging法中，在候選樣本集中篩選樣本點時需滿足以下條件：到失效面的距離越近，符號誤判的風險越大，即要求|g^k（x）|較小或σgk（x）較大，或者兩者均較大。在本文中采用了U學習函數作為自主學習Kriging法的學習函數，如下式所示：

U（x）=|g^k（x）σgk（x）|（11）

U學習函數綜合考慮了Kriging模型的預測值到失效面的距離和預測值的標準差。由式（11）可看出應該選擇使U學習函數值最小的樣本點及對應的真實函數值加入到訓練樣本集中，以更新當前Kriging模型。ECHARD等［15］提出，通常情況下可選擇min（U（x））≥2作為Kriging模型自主學習更新過程的收斂條件。

利用樣本池S中的部分樣本構造收斂的Kriging模型，命名為Kriging-Ⅰ。以Kriging-Ⅰ替代原功能函數判斷極限狀態函數的正負。在Kriging-Ⅱ的構建中，首先在樣本池S（θ）中抽取Nθ個分布參數樣本，利用Kriging-Ⅰ計算Nθ個分布參數樣本處的結構失效概率，得到Nθ組（θi，P^fi）（i=1，2，…，Nθ），然后利用該Nθ組數據構造符合精度要求的Kriging-Ⅱ。Kriging-Ⅱ即為結構失效概率函數的隱式表達式。

由于構造Kriging-Ⅰ時所需要的訓練樣本點的數目遠小于樣本池中的樣本數目，構造Kriging-Ⅱ時的訓練樣本點的響應僅是Kriging-Ⅰ模型的仿真結果，因此AK-MCS-K法的高效性可以保證。

2.2? 基本步驟

基于AK-MCS-K法估計失效概率函數的計算步驟如下：

（1）給定每個分布參數的概率密度函數fΘs（θs）（s=1，2，…，d）。理論上fΘs（θs）的選擇不影響失效概率函數Pf（θ）的計算結果，因此可以假設θ服從某一簡單分布，在本文中假定其服從均勻分布。

（2）由聯合概率密度函數fΘ（θ）生成nθ個分布參數樣本（θ1，θ2，…，θnθ）T。

（3）針對每個分布參數θi，根據fX（x|θi）生成n個輸入變量xij（j=1，2，…，n），并組合成輸入變量全空間樣本池S={x1，x2，…，xnθ}，將其用矩陣形式可表示為

S=x1x2xnθ=x11x12…x1nx21x22…x2nxnθ1xnθ2…xnθn（12）

（4）從候選樣本池S中選出輸入變量X的m個初始訓練樣本Xt=（xt1，xt2，…，xtm）T，計算相應的功能函數值gt={g（xt1），g（xt2），…，g（xtm）}。

（5）由（Xt，gt）構造（或更新）Kriging-Ⅰ模型，記為gk1（X）。

（6）利用gk1（X）對候選樣本池S中所有樣本的功能函數值進行預測，得到預測值{gk1（x1），gk1（x2），…，gk1（xnθn）}和標準差{σgk1（x1），σgk1（x2），…，σgk1（xnθn）}

（7）計算樣本池S中所有樣本點的U學習函數值，即

Uxj=|gk1（xj）|σgk1（xj）（13）

（8）滿足停止條件minj=1，2，…，nθnUxj≥2時停止更新Kriging-Ⅰ模型，執行步驟（9）；否則，加入新的訓練樣本點xu=argminj=1，2，…，nθnU（xj），令Xt←Xt∪xu，gt←gt∪g（xu），m←m+1，并返回步驟（5）。

（9）由聯合概率密度函數fΘ（θ）生成Nθ個分布參數樣本（θ1，θ2，…，θNθ）T，并利用步驟（8）中的Kriging-Ⅰ模型替代原功能函數并結合MCS法進行可靠性分析，計算每個分布參數樣本點θi處的結構失效概率PfΘ（θi）。

（10）根據步驟（9）生成的Nθ組（θi，PfΘ（θi））（i=1，2，…，N）構造符合要求的Kriging-Ⅱ模型，記為gk2。此時，gk2即為失效概率函數fΘ（θ）的隱式表達式。

3? 算例

本節中，采用極限狀態函數的非線性程度、隨機變量的維度和復雜程度不同的結構作為算例進行失效概率函數的估計。為驗證AK-MCS-K的精度及效率，分別采用本文方法和DLMCS、SLMCS、AK-MCS法求解失效概率函數。SLMCS法和AK-MCS法結合一階最大熵（first-order maximum entropy，F-MaxEnt）法擬合失效概率函數，以下分別記為SLMCS+F-MaxEnt和AK-MCS+F-MaxEnt。將DLMCS法的計算結果視為精確解。本文選取的算例均假設均值是變化的，即將均值作為未知的分布參數。為對比各種方法的優劣，本文定義了逐點相對誤差（point-by-point relative error，PPRE）EPPRE和平均相對誤差（mean relative error，MRE）EMRE，其表達式分別如下：

EPPRE=P^f（θj）－Pf（θj）Pf（θj）? j=1，2，…，M（14）

EMRE=1M∑Mj=1P^f（θj）－Pf（θj）Pf（θj）（15）

其中，M為計算EPPRE和EMRE時分布參數θ中采樣點的個數； Pf（θj）表示將分布參數θ固定在θj時用DLMCS法估計的失效概率；P^f（θj）表示將分布參數θ固定在θj時用其他方法估計的失效概率。逐點相對誤差EPPRE和平均相對誤差EMRE越小時，表明計算結果越精確。

3.1? 高非線性振子系統

高非線性振子系統是一個六變量算例，該系統如圖1所示。

該系統的功能函數為

g（c1，c2，mo，r，t1，Fa）=3r－2Famoω20sin（ωot12）（16）

ωo=（c1+c2）/mo

式中，c1、c2為兩個彈簧的剛度；mo為振子的質量；r為初始位置；t1、Fa分別為沖擊時長和沖擊幅值；ωo為該振子系統的頻率。

上述6個輸入變量均服從正態分布，且變量間相互獨立，其分布參數信息如表1所示。

（1）假設剛度的均值μc1為設計變量（即θ1=μc1），其中μc1∈［0.8，1.2］，μc2=0.1。首先從分布參數空間中均勻抽取10個采樣點，利用DLMCS法計算逐點的失效概率，每個采樣點處生成105個樣本進行失效概率的計算，此時DLMCS法的計算量為10×105=106。隨后利用SLMCS+F-MaxEnt法生成5×104個分布參數樣本估計失效概率函數，然后利用AK-MCS+F-MaxEnt法和AK-MCS-K法對失效概率函數進行估計。其中，AF-MCS+F-MaxEnt法中候選樣本池大小為5×104，初始訓練點為50個；AK-MCS-K法的樣本池大小為105，初始訓練樣本為50個。利用四種方法求得的失效概率函數如圖2所示，分布參數采樣點處誤差如圖3所示。采樣點處失效概率均值、平均相對誤差和功能函數調用次數結果如表2所示。

由圖2和圖3可看出，相對于SLMCS+F-MaxEnt法和AK-MCS+F-MaxEnt法，AK-MCS-K法在求解失效概率函數時誤差更小，對失效概率函數的擬合效果更佳。從表2中計算結果可看出，AK-MCS-K法和AK-MCS+F-MaxEnt法的計算量相當，相對于DLMCS法和SLMCS+F-MaxEnt法均顯著降低了計算量。

（2）假設剛度的均值μc1和μc2均為設計參數（即θ1=μc1，θ2=μc2），其中μc1∈［0.8，1.2］，μc1∈［0.08，0.12］。首先在兩個設計參數空間中分別抽取10個采樣點，則初始采樣點為N=10×10=100個，利用DLMCS法計算了逐點的失效概率。對于每個采樣點，生成了105個樣本點進行失效概率的計算，此時DLMCS法的總計算量為100×105=107。然后利用SLMCS+F-MaxEnt法對失效概率函數進行了估計，生成的總樣本量為5×104。最后利用AF-MCS+F-MaxEnt法和AK-MCS-K法對失效概率函數進行了估計。其中，AK-MCS+F-MaxEnt法中候選樣本池大小為5×104，AK-MCS-K法的樣本池大小為106，初始訓練樣本均為50個。利用DLMCS法和本文所提出的AK-MCS-K法求得的失效概率函數分別如圖4和圖5所示，利用四種方法在采樣點處失效概率均值、平均相對誤差和功能函數調用次數的計算結果如表3所示。

由圖4和圖5的對比可看出，AK-MCS-K法對失效概率函數的擬合情況較好，從表3中的計算結果可以直觀看出雖然AK-MCS-K法相比于

DLMCS3.4129×10-2106

SLMCS+F-MaxEnt3.3596×10-26.3654×10-45×104

AK-MCS+F-MaxEnt3.4250×10-25.8080×10-420+52

AK-MCS-K3.3699×10-28.7223×10-420+49

AK-MCS+F-MaxEnt法和SLMCS+F-MaxEnt法的誤差稍大，但在所能接受的范圍內，且AK-MCS-K法和AK-MCS+F-MaxEnt法均在滿足精度要求的同時顯著降低了計算量。

綜上，根據高非線性振子系統算例結果可看出，AK-MCS-K法擬合失效概率函數時誤差較小，且顯著降低了計算量。

3.2? 十桿桁架結構

十桿鋁桁架結構如圖6所示，所有水平桿和豎直桿的長度為L，點載荷分別為F1、F2、F3，每根桿的彈性模量均為E，截面面積為Ai（i=1，2，…，10），15個輸入變量服從正態分布且相互獨立。輸入變量的分布參數信息如表4所示，其有限元分析結果如圖7所示。根據有限元的分析結果，該結構的功能函數可定義為

g=0.0032－|Δ2|（17）

其中，Δ2=Δ（L，Ai，E，F1，F2，F3）（i=1，2，…，10）為節點2處的位移（單位為m），該位移是輸入變量的隱式函數，可以通過有限元模擬獲得。

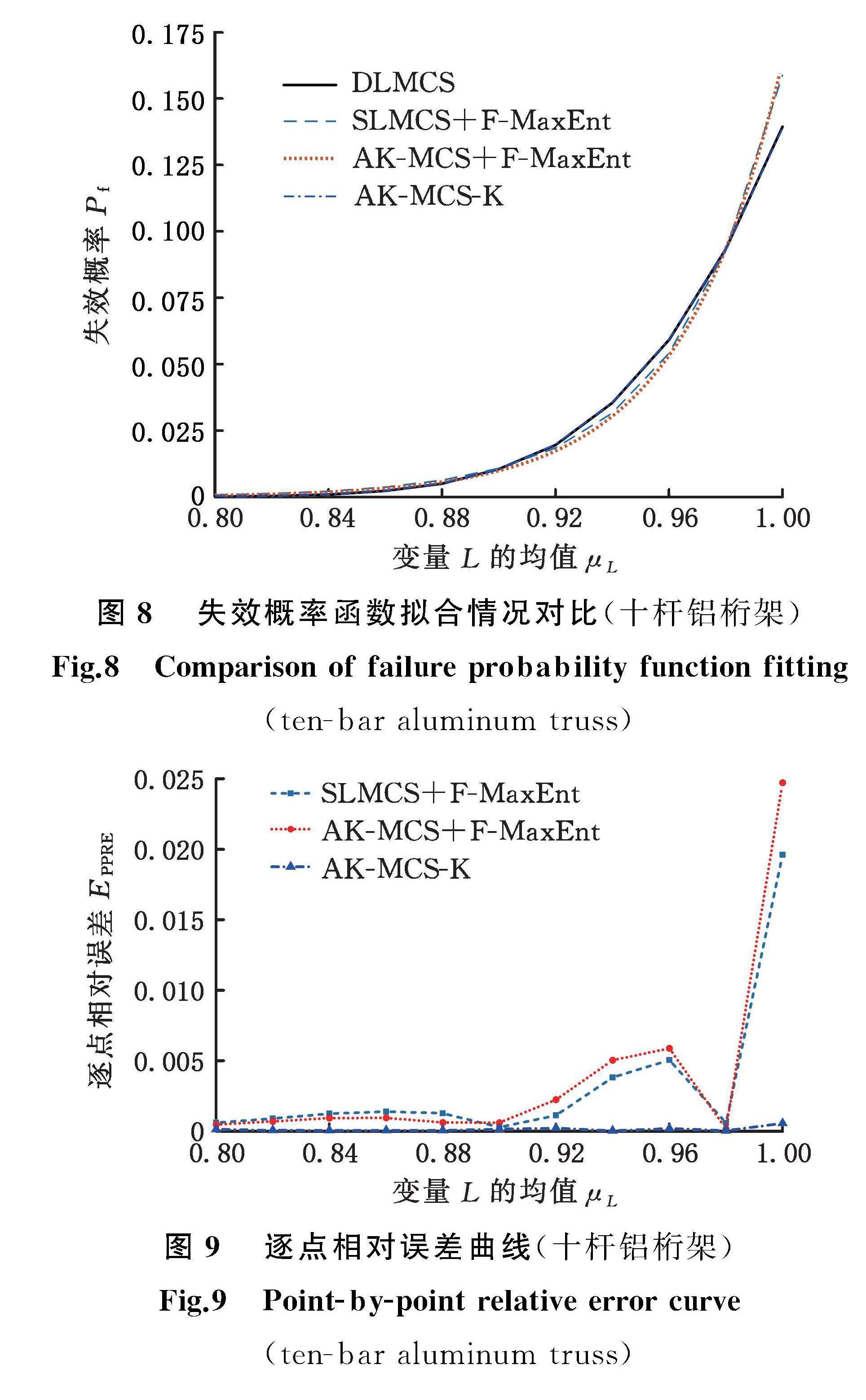
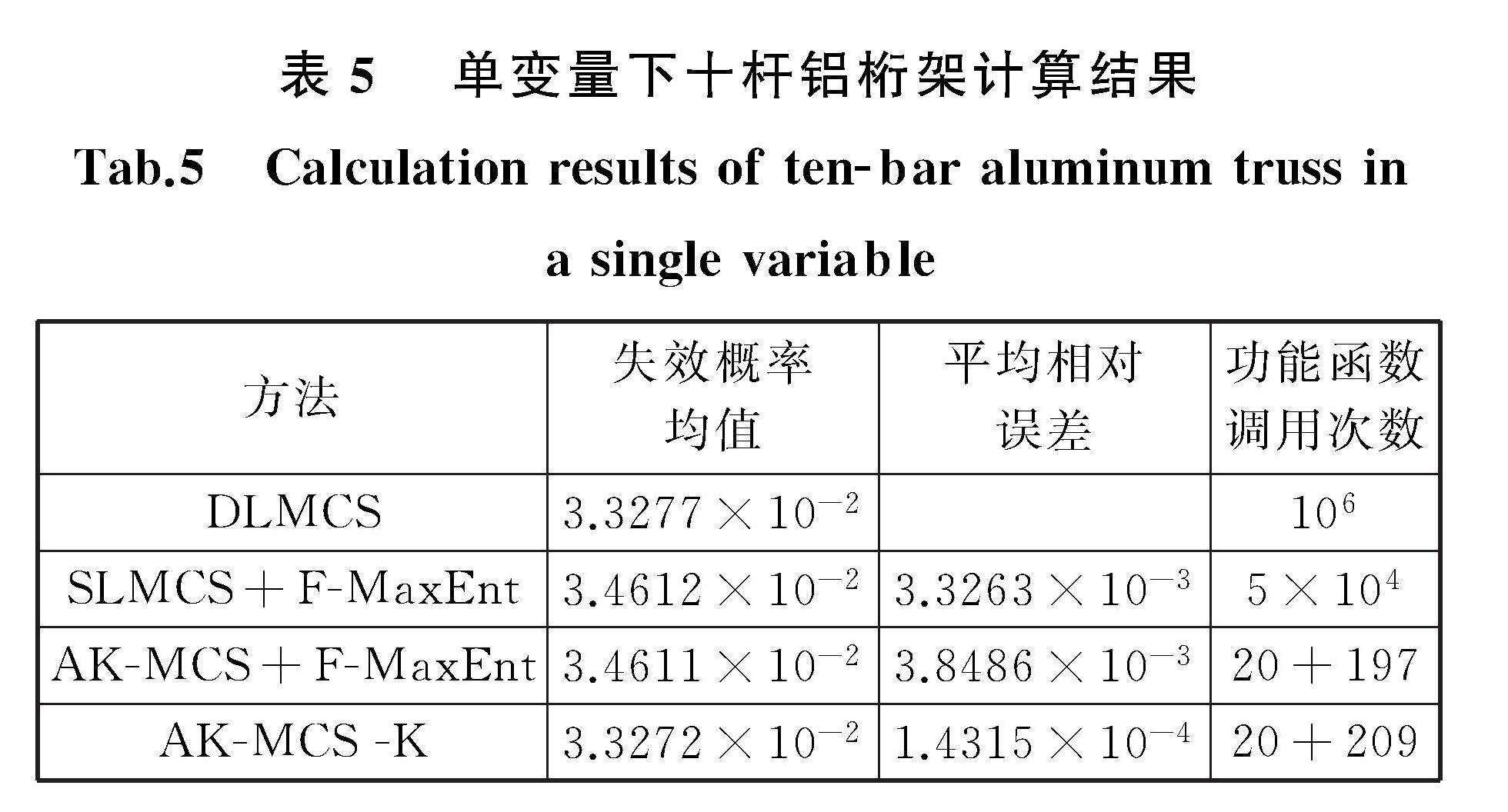
（1）假設長度L的均值為設計參數（即θ1=μL），且μL∈［0.8，1.0］。橫截面積A1的均值為μA1=0.001。四種方法求得的失效概率函數如圖8所示，分布參數采樣點處誤差如圖9所示，采樣點處失效概率均值、均值相對誤差和功能函數調用次數如表5所示。由圖8和圖9可看出AK-MCS-K法擬合失效概率函數的誤差較小，擬合效果更佳。從表5中的計算結果來看，AK-MCS-K法和AK-MCS+F-MaxEnt法的計算量相當，但擬合誤差相比AK-MCS+F-MaxEnt法和SLMCS+

F-MaxEnt法都較小，表明AK-MCS-K法具有優越性。

（2）假設長度L的均值μL和橫截面積A1的均值μA1均為設計參數（即θ1=μL，θ2=μA1），其中μL∈［0.8，1.0］，μA1∈［0.0005，0.0015］。雙變量情況下DLMCS法和AK-MCS-K法估計失效概率函數分別如圖10和圖11所示，四種方法計算的失效概率函數結果如表6所示。由圖10

和圖11可看出，AK-MCS-K法對失效概率函數的擬合情況較好，從表6中的計算結果可直觀看出，AK-MCS-K法相對于SLMCS+F-MaxEnt法和AK-MCS+F-MaxEnt法的誤差均較小，同時AK-MCS-K法與AK-MCS+F-MaxEnt法的計算量相當，這兩種方法均顯著降低了失效概率函數求解時的計算量。

綜上，根據十桿桁架算例結果可看出，AK-MCS-K法對失效概率函數的擬合效果更好，且計算量較小，表明AK-MCS-K法適用于求解復雜功能函數的失效概率函數問題。

4? 結論

針對可靠性優化設計中失效概率函數的求解難題，本文提出了一種基于自主學習Kriging方法結合Monte Carlo模擬法（MCS）和Kriging高效求解失效概率函數的新方法（AK-MCS-K法）。通過自主學習Kriging方法在輸入變量全空間內擬合失效邊界，并替代原模型判斷極限狀態函數的正負。通過MCS法計算分布參數空間中各采樣點的失效概率，最后再次利用Kriging方法進行失效概率函數的擬合。從算例結果中可以看出，AK-MCS-K法在保證精度的基礎上，其計算效率相比于DLMCS法和SLMCS+F-MaxEnt法均有大幅提高。AK-MCS-K法在估計復雜非線性功能函數的失效概率函數時有較好表現，為失效概率函數的求解提供了新思路，也為可靠性優化效率的提升打下了堅實基礎。

參考文獻：

［1］? 賀向東， 聶超. 基于貝葉斯理論的結構系統可靠性優化設計［J］. 中國機械工程， 2010， 21（6）：660-662.

HE Xiangdong， NIE Chao. Reliability Optimization Design of Structure Systems Based on Bayesian Theory［J］. China Mechanical Engineering， 2010， 21（06）：660-662.

［2］? KUSCHEL N， RACKWITZ R. Two Basic Problems in Reliability-based Structural Optimization［J］. Mathematical Methods of Operations Research， 1997， 46（3）：309-333.

［3］? LING C Y， LU Z Z， ZHANG X B. An Efficient Method Based on AK-MCS for Estimating Failure Probability Function［J］. Reliability Engineering and System Safety， 2020， 201（2）：445-468.

［4］? YUAN X K. Local Estimation of Failure Probability Function by Weighted Approach［J］. Probabilistic Engineering Mechanics， 2013， 34：1-11.

［5］? LIU W S， CHEUNG S H. Reliability Based Design Optimization with Approximate Failure Probability Function in Partitioned Design Space［J］. Reliability Engineering and System Safety， 2017， 167：602-611.

［6］? ZOU T， MAHADEVAN S. A Direct Decoupling Approach for Efficient Reliability-based Design Optimization［J］. Structural and Multidisciplinary Optimization， 2006， 31（3）：190-200.

［7］? CHENG G D， XU L， JIANG L. A Sequential Approximate Programming Strategy for Reliability-based Structural Optimization［J］. Computers and Structures， 2006， 84（21）：1353-1367.

［8］? CHING J Y， HSU W C. Transforming Reliability Limit-state Constraints into Deterministic Limit-state Constraints［J］. Structural Safety， 2008， 30（1）：11-33.

［9］? AU S K. Reliability-based Design Sensitivity by Efficient Simulation［J］. Computers and Structures， 2005， 83（14）：1048-1061.

［10］? CHING J Y， HSIEH Y H. Local Estimation of Failure Probability Function and Its Confidence Interval with Maximum Entropy Principle［J］. Probabilistic Engineering Mechanics， 2007， 22（1）：39-49.

［11］? SONG J W， VALDEBENITO M， WEI P F， et al. Non-intrusive Imprecise Stochastic Simulation by Line Sampling［J］. Structural Safety， 2020， 84（January）：101936.

［12］? ZHANG H L， ZHOU C C， ZHAO H D， et al. An Ensemble Model-based Method for Estimating Failure Probability Function with Application in Reliability-based Optimization［J］. Applied Mathematical Modelling， 2022， 108：445-468.

［13］? KAYMAZ I. Application of Kriging Method to Structural Reliability Problems［J］. Structural Safety， 2005， 27（2）：133-151.

［14］? JENSEN H A. Structural Optimization of Linear Dynamical Systems under Stochastic Excitation：a Moving Reliability Database Approach［J］. Computer Methods in Applied Mechanics and Engineering， 2005， 194（12/16）：1757-1778.

［15］? ECHARD B， GAYTON N， LEMAIRE M. AK-MCS：an Active Learning Reliability Method Combining Kriging and Monte Carlo Simulation［J］. Structural Safety， 2011， 33（2）：145-154.

（編輯? 胡佳慧）

作者簡介：

宋海征，男，1996年生，博士研究生。研究方向為結構可靠性優化、靈敏度分析等。E-mail：haizhengsong@mail.nwpu.edu.cn。

林華剛（通信作者），男，副教授。研究方向為結構動力學分析、可靠性優化設計。E-mail：huagangl@126.com。