回顧與展望


【摘要】高三數學復習備考,涉及“函數與不等式”的復習內容有很多,為了高效復習備考,文章從回顧2023年高考數學試卷(僅限于使用廣泛的兩套新高考全國卷)中“函數與不等式”內容的試題入手,結合課程標準分析其命題規律,進而展望2024年新高考數學全國卷中“函數與不等式”內容試題的特點.
【關鍵詞】函數與不等式;導數;函數的單調性;高考;展望
函數是整個高中數學的一條主線,又與不等式緊密聯系,因而“函數與不等式”(注:這里的“函數”不包括三角函數,而“導數”包括三角函數的導數;“不等式”僅指函數不等式,不包括數列不等式)是高三數學復習的重要內容之一.
考生要熟練掌握函數(特別是冪、指、對等基本初等函數及三次函數)的概念、基本性質(包括定義域、值域、單調性、奇偶性與圖象),了解其他性質(包括連續性、周期性、對稱性、有界性、可導性、凹凸性、極值與最值等).函數最重要的性質是單調性:若求出了一個函數的所有單調區間,就可畫出該函數的圖象,進而可得到該函數的極值、最值、值域等等性質[1].
2023年高考數學試卷共7套[2],其使用情況見文.2024年高考數學試卷也是同樣的7套,其中地方自主命題卷3套:北京、天津、上海;全國卷4套(其使用情況謹供讀者參考):甲卷(分文科與理科,四川、西藏共2個省區使用)、乙卷(分文科與理科,內蒙古、陜西、青海、寧夏、新疆、山西、河南共7個省區使用)、新高考卷Ⅰ(下簡稱卷Ⅰ)(山東、廣東、湖南、湖北、河北、江蘇、福建、浙江共8個省使用)、新高考卷Ⅱ(下簡稱卷Ⅱ)(遼寧、重慶、海南、云南、甘肅、黑龍江、吉林、安徽、江西、貴州、廣西共11個省市使用).
涉及“函數與不等式”的復習內容有很多,為了高效復習備考,本文將從回顧2023年高考數學試卷(僅限于使用廣泛的兩套新高考全國卷)中“函數與不等式”內容的試題入手,結合教育部制定的《普通高中課程標準(2017年版2020年修訂)》[3]分析其命題規律,進而展望2024年新高考數學試卷中“函數與不等式”內容試題的特點.
文章內容僅代表個人觀點,謹供讀者參考.
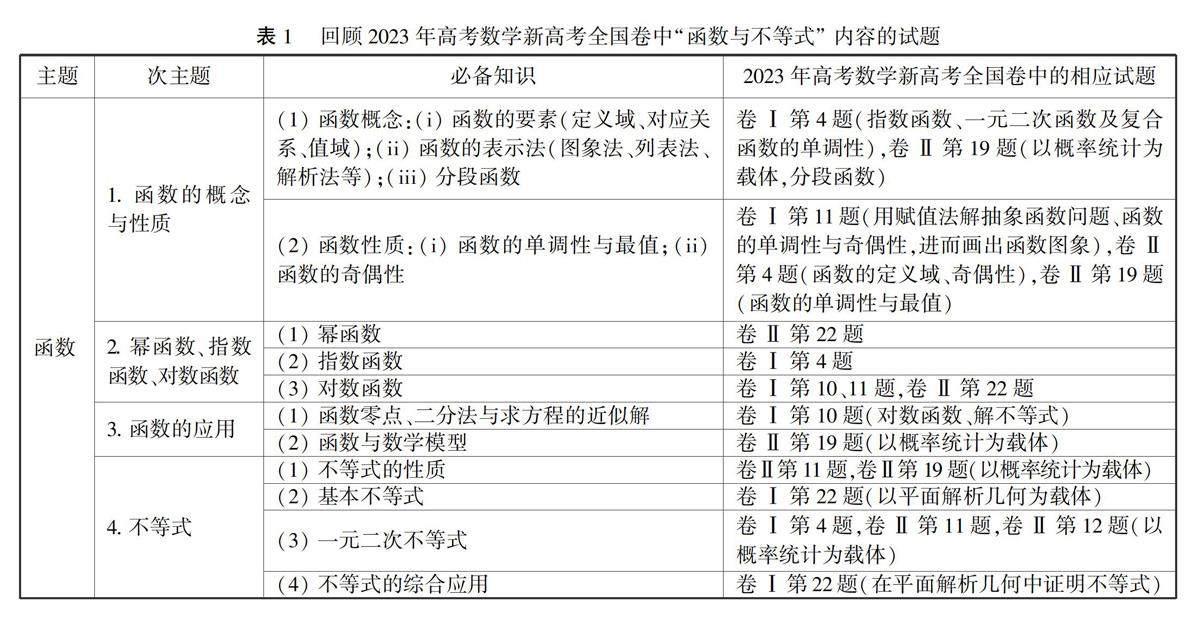
1回顧2023年高考數學新高考全國卷中“函數與不等式”內容的試題
2023年高考數學新高考全國卷中的相應試題
函數
1.函數的概念與性質
2.冪函數、指數函數、對數函數
3.函數的應用
4.不等式
2.12其他重點問題
函數零點問題依然是重要題型,函數不等式是難度較大的題目、雙參數問題可能出現(分別見文的第2.7,2.8節;證明函數不等式的常用方法見文).極值點偏移問題(其難度較大)涉及函數零點及函數不等式,其解法可見文.
讀者還應關注絕對值函數問題的解法(其難度較大).另外,涉及函數與不等式的多項選擇題、數學文化試題[16]及結構不良問題(比如2021年新高考全國卷Ⅱ第22題)也是近年高考試題的熱點.結構不良問題較結構良好問題多了一項考查功能:考查考生對選項難易程度的甄別,及對所求問題進行合理搭配再完成求解的能力.
《中國高考報告2023》[17]中還提出2023年數學高考的命題變化“數學的命題方式將加入復雜情景,重點強調對數學思維方法的考查”,還提出2023年數學高考命題的四大趨勢:落實立德樹人,鮮明體現時代主題;高考由“考知識”向“考能力”轉變;聚焦“關鍵能力”和“思維品質”的考查;高考由“以綱定考”到“考教銜接”轉變.這些對2024年的數學高考也有重要指導意義.
關于高三數學復習備考策略,在筆者發表的文章中已闡述較多,比如文及其文末列出的參考文獻,有興趣的讀者可研讀.
參考文獻
[1]甘志國.回顧與展望:以高考數學全國卷中函數與不等式的內容為例.中學數學雜志,2022(03):32-38.
[2]蔣海燕,甘志國.2023年高考“函數與導數”復習指導.中學數學雜志,2023(05):23-28.
[3]中華人民共和國教育部.普通高中課程標準:2017年版2020年修訂.2版.北京:人民教育出版社,2020.
[4]甘志國.關于函數圖象的對稱性與周期性的幾個結論.數理化學習(高中版),2022(01):3-4.
[5]甘志國.函數y=lnxx的單調性及其應用.中學數學雜志,2015(11):34-37.
[6]甘志國.2023年高考數學新課標全國卷Ⅰ第11題的背景是柯西方程.中學生理科應試,2023(08):17-18.
[7]甘志國.“考查素養、引導教學”是2023年高考數學北京卷的鮮明特色.中學數學雜志,2023(09):47-53.
[8]甘志國.用指數對數恒等式x=elnx簡便解題.高中數學教與學,2020(05):7-9.
[9]甘志國.立德樹人服務選才引導教學:賞析2022年高考數學北京卷.中學數學雜志,2022(09):42-47.
[10]甘志國.簡解2016年高考全國卷Ⅲ文科第21(3)題.數理化解題研究,2017(10):23.
[11]甘志國.不可忽視的非等價轉化解題.高中數學教與學,2016(03):13-15.
[12]甘志國.用導數證明函數不等式的4種常用方法.高中數理化,2018(03):6-8.
[13]甘志國.在極值點偏移問題中證明二元不等式時的兩種常規策略及其優化.數理化學習(高中版),2023(08):9-13.
[14]甘志國.談談極值點偏移問題的解法:以2021年新高考全國卷Ⅰ壓軸題為例.湖北招生考試,2021(34):49-53.
[15]甘志國.研究極值點偏移問題的新方法.中學生理科應試,2021(11):12-14.
[16]甘志國.數學文化與高考研究.哈爾濱:哈爾濱工業大學出版社,2018.
[17]中國高考報告學術委員會.中國高考報告2023.北京:新華出版社,2023.

