基于改進四叉樹和比例邊界有限元法的自適應設計域拓撲優化方法

王浩 王江北 羅浩東 王立文

摘要：

針對大型結構拓撲優化計算成本高和固體各向同性材料懲罰模型（SIMP）在優化后結構邊界處求解精度低的問題，提出了一種基于SIMP法的自適應設計域（ADD）拓撲優化方法。將改進四叉樹法應用在拓撲優化的過程中，通過自動劃分不同等級的網格單元來減少網格數量、減輕計算負擔并提高邊界處求解精度；采用比例邊界有限元法（SBFEM）實時計算劃分后結構的有限元信息，解決了不同等級網格間懸掛節點的問題。所提方法可在初始網格相對較少的情況下得到更加精確的結果，大幅度地降低了計算成本。數值算例結果表明，所提方法在最終結構邊界處精度相同的情況下，計算時間最快可縮短為原來的1/100，可以為后續降低大型結構拓撲優化的計算成本提供參考。

關鍵詞：拓撲優化；改進四叉樹法；比例邊界有限元法；網格自適應

中圖分類號：TH122

DOI：10.3969/j.issn.1004132X.2024.05.016

開放科學（資源服務）標識碼（OSID）：

An Adaptive Design Domain Topology Optimization Method Based on

Improved Quadtree and SBFEM

WANG Hao1，2? WANG Jiangbei3? LUO Haodong3? WANG Liwen4

1.College of Safety Science and Engineering，Civil Aviation University of China，Tianjin，300300

2.Engineering Techniques Training Center，Civil Aviation University of China，Tianjin，300300

3.College of Aeronautical Engineering，Civil Aviation University of China，Tianjin，300300

4.Institute of Science and Technology lnnovation，Civil Aviation University of China，Tianjin，300300

Abstract： Aiming at the problems of high computational cost of large-scale structure topology optimization and low solving accuracy of solid isotropic material with penalization（SIMP） at the optimized structure boundary， an adaptive design domain（ADD） topology optimization method was proposed based on SIMP. The improved quadtree method was applied in the processes of topology optimization to reduce the computational burden and improve the solution accuracy at the boundaries through different levels of grid cell. The SBFEM was used to calculate the finite element information of the partitioned structures in real-time， solving the problem of hanging nodes between different level cells. The proposed method might obtain more accurate results with fewer initial grids and significantly reduce the computational cost. Numerical example results demonstrate that， with the same final structural boundary accuracy， the proposed method may reduce the computation time to 1/100 of the original at most， offering a reference for reducing the computational cost of large-scale structural topology optimization in subsequent processes.

Key words： topology optimization; improved quadtree method; scaled boundary finite element method（SBFEM）; grid adaptation

收稿日期：20230914

基金項目：國家自然科學基金民航聯合研究基金重點項目（U2133202）；四川省重大科技專項（2021ZDZX0001）；中國民航大學研究生科研創新項目（2022YJS058）

0? 引言

拓撲優化方法是一種給定約束和目標函數，在規定設計域內對結構材料進行尋優的算法，可以對結構零件進行輕量化設計。目前，該方法已被廣泛地應用于航空航天、汽車工程、機械工程、海洋工程［1-6］等領域。早期由于計算條件的限制，主要應用于小型結構件，隨著有限元的發展，越來越多的大型結構［7］也會采用拓撲優化方法來達到減重的目的。

在航空航天領域中，飛機機身、發動機吊架、機翼前緣翼肋等大尺寸且具有高精度要求的零件，動輒需要幾十萬個網格單元，直接求解帶來的計算負擔讓人望而卻步，因此尋找一種適用于具有大量網格或大型結構的拓撲優化方法具有重要研究意義。

拓撲優化過程需要反復迭代，每次迭代過程都需要對結構進行性能分析，有限元計算占比較大，其中網格數量直接影響最終的計算時間。PRAMOD等［8］提出了利用自適應相場方法模擬脆性斷裂，將所需網格數量減少為原來的1/10； BAIGES等［9］采用自適應有限元網格和降階模型使計算效率提高11倍；INNERBERGER等［10］通過對三角形網格的細化，更加快速地求解了非線性偏微分方程的迭代線性化方法引起的問題。許多研究人員通過網格自適應的方法來對有限元網格數量進行控制，從而減輕計算負擔。

基于改進四叉樹和比例邊界有限元法的自適應設計域拓撲優化方法——王? 浩? 王江北? 羅浩東等

中國機械工程 第35卷 第5期 2024年5月

網格自適應算法中，四叉樹算法的靈活性強、計算效率高、精度高，最早被應用于計算機圖像學領域，是一種圖像壓縮算法，后被遷移到工程計算中，主要應用在求解尖端裂紋、應力強度因子［11-14］等方面。孫立國等［15］將水平集函數與圖像四叉樹法相結合對網格進行自適應劃分，求解了復合型應力強度因子； GRAVENKAMP等［16］將四叉樹與比例邊界有限元法（scaled boundary finite element method， SBFEM）相結合對復雜幾何形狀的靜態、諧波、模態和瞬態分析等的數值算例進行了分析。CORNEJO等［17］利用自適應網格與有限元法和離散元法耦合的方法，實現了在變量場曲率較大處細化網格，并對裂紋的擴展進行了分析。WIJESINGHE等［18］將數字圖像網格與SBFEM相結合，用于巖土邊坡穩定性分析的數值技術研究。

在斷裂力學中裂紋源位置是已知的，四叉樹算法可以準確地在裂紋尖端處進行網格自適應劃分。拓撲優化過程中生成的拓撲結構具有未知性，傳統四叉樹算法無法準確得到所需細化網格的位置，因此在拓撲優化過程中傳統的四叉樹細化策略失效。

改進四叉樹算法將拓撲優化結構中的密度值作為細化策略的判定條件，從而應用到拓撲優化中。細化結構邊界處的網格，可以大幅度提高拓撲優化結構邊界處的精度。經改進四叉樹算法細化后的拓撲優化結構具有不同等級的網格單元，首先通過SBFEM更新整體結構剛度矩陣，然后進行迭代優化。

本文將改進四叉樹算法和SBFEM相結合自適應地更新設計域內網格，提出了一種基于固體各向同性材料懲罰模型（solid isotropic material with penalization， SIMP）方法的自適應設計域（adaptive design domain，ADD）拓撲優化算法（以下簡稱“ADD-SIMP方法”）。本文詳細介紹了ADD-SIMP方法，給出了SBFEM的推導過程，并通過兩個數值案例對所提方法進行了驗證。ADD-SIMP方法可以通過更少的初始網格數量獲得邊界處相同精度的求解結果，大幅度降低了計算成本，可為大型結構的拓撲優化提供參考。

1? ADD-SIMP模型

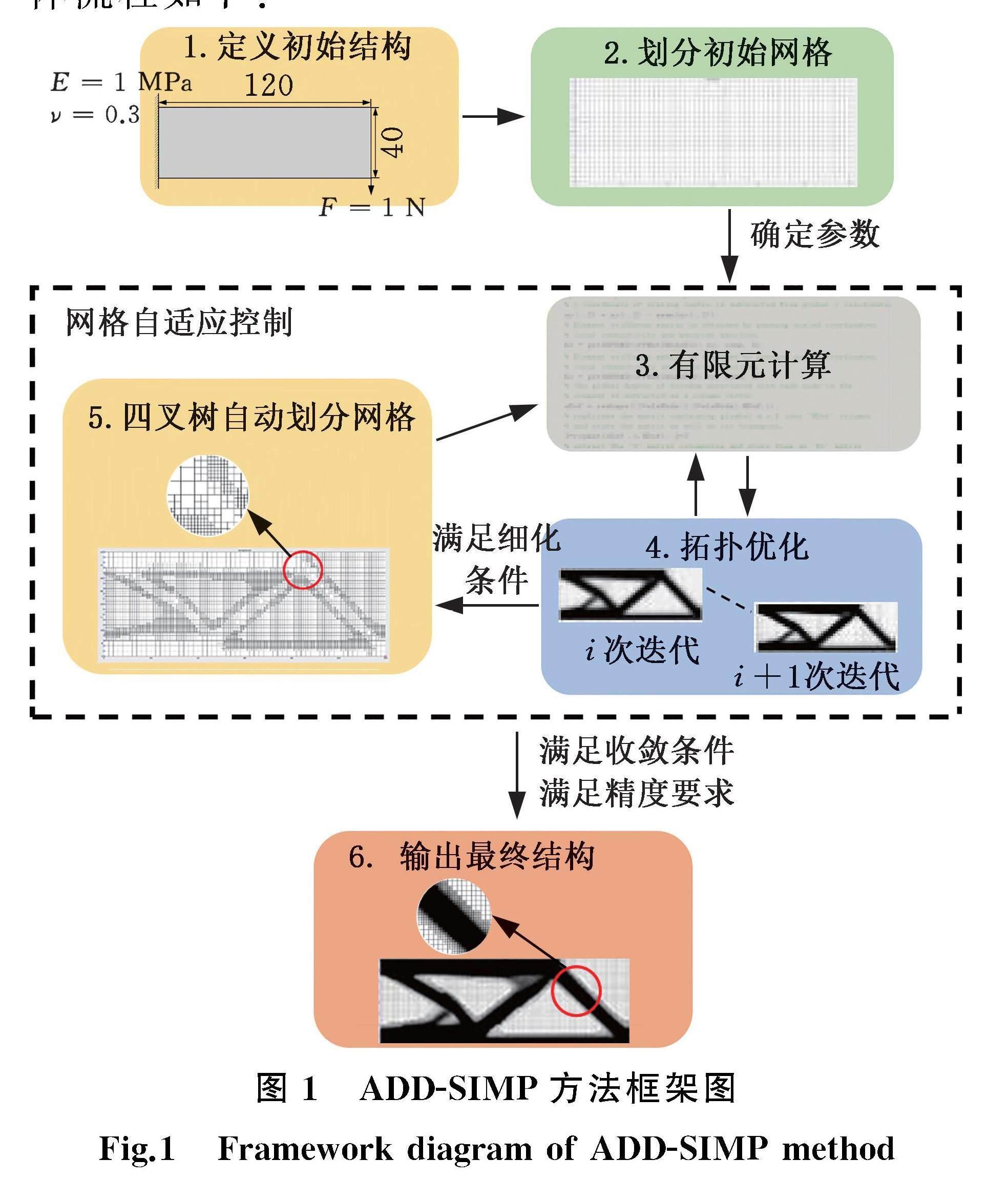
ADD-SIMP方法的整體框架如圖1所示，具體流程如下：

（1）給定結構幾何參數、材料參數、優化目標和約束等條件。

（2）根據需求設置初始網格劃分以及最小網格單元等級等參數。

（3）有限元計算得到每個單元的位移場、剛度矩陣等有限元參數，計算結構柔度和靈敏度，并對單元靈敏度進行更新。

（4）通過優化準則（optimality criteria，OC）進行初步優化，當結構初步穩定時執行步驟（5）。

（5）通過改進四叉樹算法對結構邊界網格進行自動加密，以達到精確結構邊界位置的目的；迭代步驟（2）～步驟（5），直到結構最小網格單元等級滿足步驟（1）中規定的最小網格單元等級時不再對網格進行細化。

（6）對該結構繼續進行拓撲優化，直至最終結構滿足收斂條件后輸出該結構。

1.1? SIMP方法

固體各向同性材料懲罰模型（SIMP）［19］方法因其簡單易懂、靈活性強、可擴展性好等優點成為目前主流的拓撲優化方法之一。但SIMP法生成的拓撲結構往往會存在大量的偽密度單元，如圖2所示，在結構邊界處偽密度單元數量約為實體單元數量的3倍，這會致結構邊界處的求解精度受到限制，反映了較低的精度水平。精度要求高的大型結構就需要更多數量的網格來提高精度。

本文基于將結構的體積作為約束、最小柔度作為目標的拓撲優化問題進行了網格自適應的研究，其中優化問題的表達式如下：

其中優化問題的表達式為

find X=（x1，x2，…，xN）T∈D

min C=∑Ni=1xp0iuTikiui

s.t. V=φV0=∑Ni=1xiVi

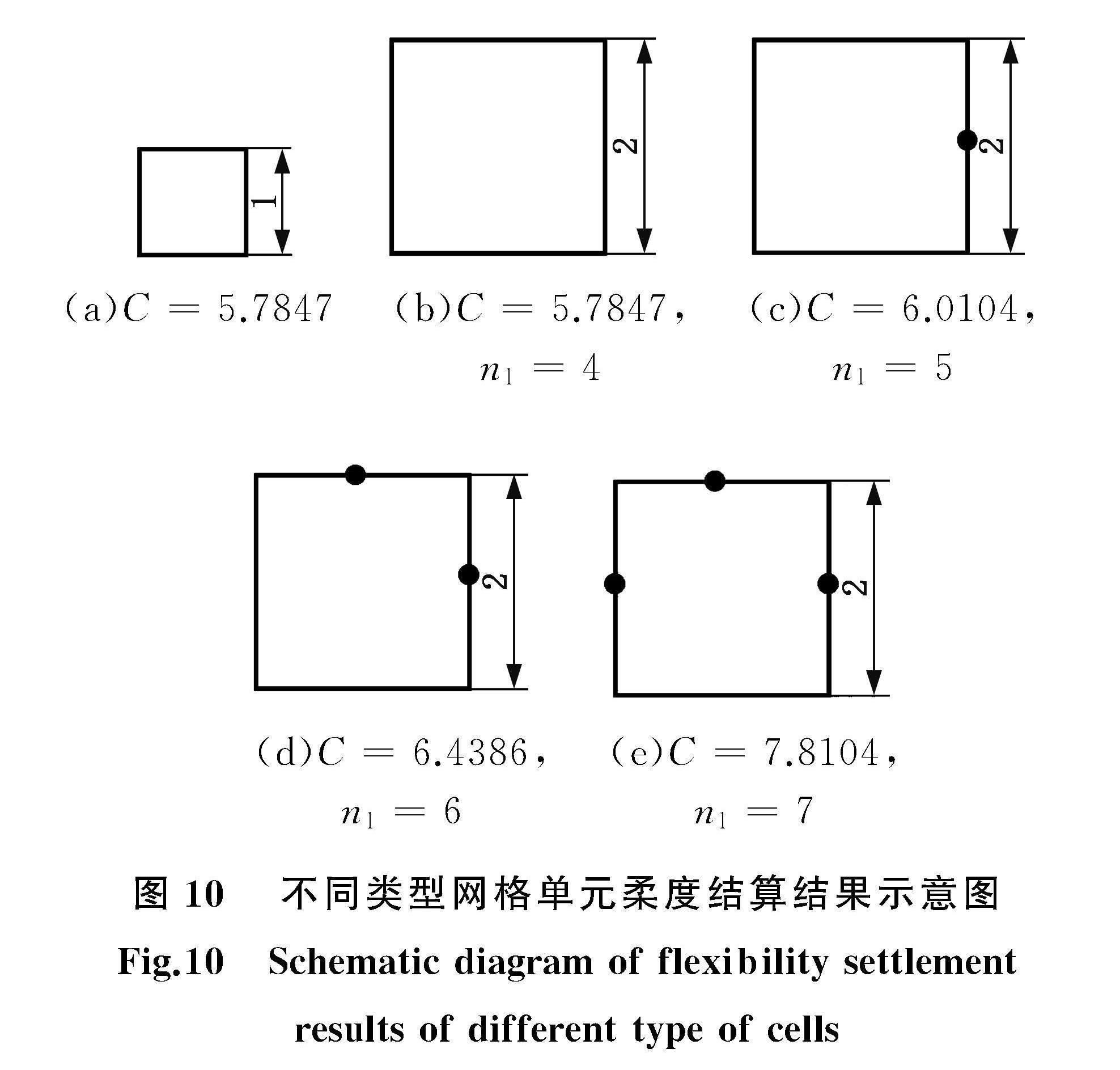
0

式中，X為結構設計域內單元的相對密度；xi、ui、ki、Vi分別為第i個單元的相對密度、位移矢量、剛度矩陣、體積；N為設計域內單元的總數；D為結構總設計域；C為結構柔度；p0為懲罰因子，工程上一般取p0= 3；V為結構總體積；V0為結構初始體積；φ為目標體積分數；xmin為單元相對密度值的下限，為了計算穩定，防止出現奇異性，一般設置xmin=0.001。

1.2? 改進四叉樹算法

四叉樹是一種數據結構，主要應用于計算機圖像學領域，本文引入一種改進四叉樹算法對拓撲優化過程中的網格進行自適應劃分。通過采用新的細化策略、網格單元和節點存儲方式，實現拓撲優化過程中的網格自適應控制，以提高計算效率并提高邊界處的精度，其中網格單元儲存于單元樹（cellMap）中，用于儲存結構網格單元的材料、位置等信息，具體參數含義詳見表1；節點存儲于節點樹（nodeMap）中，用于存儲節點位置和編號信息，具體參數含義詳見表2。兩個數據結構共同完成結構拓撲優化過程的網格實時更新。

1.2.1? 網格單元與節點存儲

圖3所示為單元細化后新增子單元與新增節點情況，其中新增網格單元順序如圖3a所示，新增節點順序如圖3b所示，角節點的序號不變，將新增節點作為新節點插入節點樹中。

每個網格單元有唯一的標識符與之對應，單元標識符的計算公式依靠單元結構中的單元等級lc和單元索引ic共同決定。lc=0表示該網格為初始網格，lc=h表示初始網格劃分h次后的h級網格，網格等級每增加1級，網格單元尺寸則會變為原來的1/2，邊界處的精度也隨之提高。

每次劃分每個單元時最多可以劃分為4lc個單元，為防止重復單元標識符出現，假設每級單元完全細化，并在此基礎上計算新網格單元編號，因此對于一個n行m列的結構中當前網格單元等級為h、單元索引為（x，y）的單元，其唯一標識符kc的計算表達式如下：

kc=2h（y-1）m+x+∑hlc=14（lc－1）mn （2）

細化后出現的單元索引可由下式計算得到：

ic，pa=（p，q）

ic，ch（1，1）=（2p－1，2q－1）

ic，ch（1，2）=（2p－1，2q）

ic，ch（2，1）=（2p，2q－1）

ic，ch（2，2）=（2p，2q）（3）

其中，p、q為父級單元的索引ic，pa。得到子網格的索引ic，ch后通過式（2）計算出子網格的編號。

需要說明的是，節點唯一標識符kn由 x、y方向上的標識符kn，x和kn，y構成，其計算由給定結構的尺寸參數、最小細化等級共同決定。最小細化等級為初始網格大小和設定的最小單元尺寸共同決定，單個網格邊界上最多可以劃分2lc，max+1個節點（其中lc，max為當前最高單元等級），單元真實最小尺寸smin為單元尺寸sc除以2lc，max，根據單元位置坐標Pn（Pn，x，Pn，y）可計算得到節點的kn，x和kn，y，則節點唯一標識符kn通過下式確定：

sc2lc，max=smin? lc，max∈Z

kn，x=floor（Pn，xsmin）

kn，y=floor（Pn，ysmin）

kn=kn，x_kn，y（4）

其中，floor（·）表示向下取整函數。

由于節點標識符不具有連續性，因此節點標識符的作用僅為確定設計域中的某個唯一節點，為后續計算的順利進行需要引入連續的節點編號nn作進一步處理，具體流程如下：

（1）計算新增節點的唯一標識符kn。根據新增節點的位置信息，利用式（4）可以計算出該節點的kn。

（2）依據步驟（1）中計算出的kn，在節點樹中搜索出對應的節點。

（3）若節點樹中不存在相應kn的節點（即返回值為空），則新增節點，賦予其節點編號（即當前節點樹中最大節點編號值加1），并加入節點樹；若已存在，則保持原節點所有信息不變。

有限元計算需要將網格單元中的節點按逆時針排序，因此網格單元通過左下角節點的位置進行定位，如圖4中網格單元3的節點順序為｛1，2，5，3，6，4｝。

圖4中，節點5、6（僅列舉出了圖中標出節點）為T型節點，SBFEM與FEM計算得到的位移場的誤差最大為8%，最小為0.9%。同時為防止某個網格單元具有過多的T型節點而導致計算數值不穩定，因此新增網格單元等級控制策略，其具體步驟如下：

（1）讀取當前單元的ic，并計算得到相鄰所有單元索引的集合。

（2）根據式（2）計算出相鄰單元的kc值。

（3）讀取單元樹中對應kc值下的單元信息，若返回空數組則表示單元不存在，通過計算得出父級單元的ic，pa并通過式（2）計算出kc，pa值，讀取單元樹對應的網格單元信息，若仍返回空數組則表示單元等級差超過1，并對父級單元的上級單元進行網格劃分。父級單元的索引ic，pa可表示為

ic，pa=k??? ic∈2k??? k=1，2，…

k+1ic∈2k+1k=1，2，…（5）

1.2.2? 細化策略

當拓撲優化中兩次輸出結構的單元最大改變量小于設定閾值時對結構進行細分，該閾值為細化閾值，為網格是否需要細化的判定條件。細化閾值的選取影響了網格細化時主承力結構是否出現。為保證拓撲優化結構的穩定，將細化策略分為網格細化和網格檢查兩步。

網格細化的目標單元主要是生成的拓撲優化中所有偽密度單元和已經穩定的邊界單元，其余單元不參與網格的細化。通過網格細化可以獲得不同等級的網格單元，從而大幅度減少網格數量，提高網格的利用率和計算效率。網格細化后的效果如圖5所示。

網格檢查的目的是對細化后的整體網格單元進行檢查，對網格細化后不滿足要求的網格單元進行細化。網格檢查的目標為當前最大單元等級的上兩級單元。網格檢查步驟可以有效緩解鋸齒邊界的出現，鋸齒邊界如圖6所示。

鋸齒邊界主要是由網格細化后主承力結構在后續變化中移動至粗網格邊界處所產生的。鋸齒邊界出現的原因在于有限元方法由傳統有限元法替換為SBFEM后，靈敏度的改變引起優化準則出現不穩定現象。

細化策略中網格細化的具體步驟包括：

（1）從單元樹中讀取所有網格單元信息，提取的目標單元為所有未細化的網格單元。

（2）對未細化單元中所有偽密度單元進行細化。將懲罰因子p0設置為3，當單元相對密度x=0.1時，被懲罰后參與計算的實際相對密度值約為0.001；當x=0.8時，被懲罰后的相對密度值約為0.5，因此過程中參與細化的網格單元的單元相對密度值位于0.1～0.8。

（3）對于單元相對密度值大于0.8的網格單元，讀取與該單元相鄰的4個單元的密度值進行判斷，若相鄰單元中存在單元相對密度值小于0.8的網格單元，表明該單元處在結構邊界處，則對單元進行網格細化。

網格檢查的具體步驟包括：

（1）讀取所有處于當前網格最高等級上一級單元的網格，圖7中灰色單元為當前最高等級單元，紅色單元為上一級網格單元。

（2）獲取中心單元所在九宮格中所有的網格單元，計算9個單元的平均相對密度值。

（3）若平均相對密度值小于1且大于0.1，表明該單元為鋸齒邊界處單元，則對該單元進行細化。

圖8為經過網格檢查后，結構經第二次網格細化之后的效果圖，可以看出鋸齒邊界得到明顯改善。

1.3? 靈敏度分析與網格無關濾波器

對于細化后的網格，靈敏度更新策略與傳統方式不同。在傳統有限元中以每個網格單元為單位，其剛度矩陣為常數，因此每個單元對整體結構的靈敏度可以直接求解。隨著網格被細化后懸掛節點的出現，傳統的有限元算法失效，因此需要引入SBFEM來計算剛度矩陣等有限元信息。

SBFEM中每個網格由若干個線單元構成，細化后會產生不同等級單元相互接觸的情況，如圖9所示，其中3號單元包含6個線單元，而4號單元只包含4個線單元，計算得到3號單元的靈敏度要高于4號單元的靈敏度，因此由多個單元組成的網格的靈敏度要高于其他四邊形網格的靈敏度。

如圖10所示，單元柔度C與單元長度無關，與線單元的數量nl有關。

單元靈敏度受到網格中單元個數的顯著影響，為降低由于線單元數量不同所帶來的影響，進行了歸一化處理。具體操作是，將所有包含線單元的網格統一歸一化為四邊形單元。這樣的處理旨在降低不同數量的線單元對單元靈敏度的影響。為此，引入了一個新的修正公式來更加準確地評估單元靈敏度，以減少評估結果因網格中線單元的數量差異而產生的偏差，修正公式如下：

d=p0xp0－1C［1－（1－4nl）2］=8p0xp0－1Cnl－2n2l（6）

（a）C=5.7847? （b）C=5.7847，nl=4? （c）C=6.0104，nl=5

（d）C=6.4386，nl=6? （e）C=7.8104，nl=7

results of different type of cells

其中，為修正后的單元柔度，修正后的值如表3所示。

為防止出現棋盤網格現象，需要對過濾半徑rmin內所有網格單元進行靈敏度過濾處理。為節省計算資源，從中心單元j開始，搜索以單元j為中心、過濾半徑rmin內所有未劃分的網格單元，讀取rmin內所有網格單元的靈敏度，并根據下式對中心網格單元的靈敏度進行更新：

dc^j=1xj∑Mm=1H^m∑Mm=1H^mxmcmxm（7）

H^m=max（0，rmin－dist（j，m））

{M∈N|dist（j，m）≤rmin}

式中，c^j為修正后中心單元j的柔度；xj為當前中心單元j的相對密度；M為過濾半徑rmin內的單元個數；xm為過濾半徑內第m個單元（以下簡稱m單元）的相對密度；cmxm為m單元的靈敏度；H^m為m單元對中心單元的影響系數；dist（j，m）表示m單元與中心單元j的距離，距離越大，m單元對中心單元的影響系數越小。

搜索網格單元時可分為如下兩種情況。

（1）高等級網格單元為中心時的情況如圖11a所示，當將一個高等級（更細分）的網格單元作為中心進行搜索時，過濾半徑內可能會發現一些等級低于中心單元（尺寸較大）等級的網格單元。若搜索時與中心單元等級相同的鄰近單元1不存在，則會返回空結構數組，此時需要通過式（5）來計算獲取網格單元1的父級單元索引，并調用父級網格單元的靈敏度來參與計算，以確保考慮到高等級中心網格單元周圍較大尺寸單元的影響。

（2）低等級網格單元為中心時的情況如圖11b所示，當將一個低等級（即尺寸較大）的網格單元作為中心時，過濾半徑內可能存在一些高等級的網格單元。與第一種情況不同，這時由于鄰近單元（以灰色表示）實際存在，搜索不會返回空結構數組。在這種場景下，需要增加額外的判斷條件來檢查rmin半徑內的網格單元是否已經被細分。如果這些網格單元已經被細分，則需要通過式（3）計算獲取子網格的單元索引，并調用子網格單元的靈敏度來參與計算，以確保在以較大尺寸單元為中心時能夠適當考慮到周圍被細分的較小網格單元的影響。

1.4? 網格自適應流程

ADD-SIMP方法中的網格自適應主要是通過改進四叉樹算法來對邊界處的網格進行自動細化，并進行拓撲變量的更新。具體流程如下：

（1）檢查細化條件。判斷是否滿足網格細化的閾值條件。

（2）網格細化。若滿足細化條件則將偽密度單元劃分為四個小網格單元，并傳遞拓撲信息。

（3）網格檢查。對細化后的網格進行檢查，處理非正常網格。

（4）更新設計變量。將新生成的小網格與未細化的大網格組合，并參與后續拓撲優化。

（5）檢查最小網格要求。判斷是否滿足最小網格要求，若不滿足則返回步驟（1）。

（6）優化輸出結構。若滿足最小網格要求則完成優化并輸出結構。

2? SBFEM方法

2.1? 理論推導

由于網格局部劃分，新增的懸掛節點使傳統的全解析有限元計算方法失效。SBFEM是一種半解析算法［20］。傳統有限元方法通過使用所有角節點進行網格單元的拼裝，而SBFEM則通過將四邊形單元離散為四個線單元，并將具有懸掛節點的線單元分割成兩個線單元的組合，從而避免了懸掛節點處無法計算的問題，因此相較于傳統的有限元方法，SBFEM更適用于改進四叉樹算法對網格進行劃分后的有限元計算。

對于以柔度為目標的拓撲優化流程的有限元分析，主要需要求解單元上的位移場和單元剛度矩陣，因此面臨的主要問題是求解偽密度單元上的應變場和具有懸掛節點的單元剛度矩陣的問題。

笛卡兒坐標系中（x，y）與自然坐標系（ξ，η）的轉換關系如圖12所示，其中位于邊界上的節點B（xB，yB）所對應的自然坐標系下的計算表達式如下：

xB=ξx（η）=ξN（η）x

yB=ξy（η）=ξN（η）y（8）

其中，N（η）表示2節點線單元形函數，η為邊界插值坐標；ξ為放縮系數，當ξ=1時表示節點B位于邊界上，ξ=0表示節點B位于縮放中心O處。

SBFEM中位移方程u在自然坐標系下的表達式如下：

u（ξ，η）=ξN（η）u（9）

應變位移關系如下：

ε（ξ，η）=Lu（ξ，η）（10）

其中，L為微分算子矩陣，ε為應變方程。則線單元上應力的表達式如下：

σ（ξ，η）=Dε（ξ，η）（11）

其中，D為剛度系數矩陣。

根據虛功原理可以得到控制方程，其中E0、E1、E2為與線單元幾何有關的常系數矩陣。設式中自由度為n，通過引入變量式，將控制方程變為自由度為2n的一階常微分方程，具體表達式如下：

E0ξ2u″（ξ）+（E0+ET1－E1）ξu′（ξ）－E2u（ξ）=0

X（ξ）=u（ξ）q（ξ）

ξX′（ξ）=－ZX（ξ）

Z=E－10ET1－E－10－E2+E1E－10ET1－E1E－10（12）

式中，u（ξ）為節點位移矢量；q（ξ）為節點力矢量；u′（ξ）、u″（ξ）分別為u對變量ξ的一階偏導和二階偏導;X′（ξ）為X（ξ）的一階偏導;Z為哈密頓矩陣。

通過求解哈密頓矩陣的特征值λ和特征向量矩陣Φ，再結合邊界條件中的特殊點，可以求解得到積分常數c，其表達式如下：

X（ξ）=Φuλuc

Φqλqc（13）

結合式（12）和式（13），可得等效節點力矢量方程為

q（ξ）=ΦqΦ－1uu（ξ）=Keu（ξ）（14）

其中，Φu、Φq和λu、λq分別為與u和q相關的特征向量矩陣和特征值；Ke為單元剛度矩陣。根據式（14），當ξ =1時可以得到邊界處力與位移的關系，則宏觀結構上力與位移的關系表達式為

F=KU（15）

其中，F為結構外載荷矢量；U為結構位移矢量；K為總體剛度矩陣。結合式（14）和式（15），可得總體剛度矩陣的計算公式為

K=ΦqΦ－1u（16）

則SIMP插值后的單元剛度矩陣可表示為

Ke=ρp0eΦqΦ－1u

式中，ρe為單元密度。

2.2? 有限元信息更新

在SIMP方法中，所有網格都要通過有限元計算獲得應力場等其他有限元信息，其中關鍵是得到每個網格單元的剛度矩陣。經過改進四叉樹算法細化后的結構會增加大量具有懸掛節點的網格單元，因此，每次經過網格細化后的整體結構剛度矩陣需要得到實時更新。

SBFEM算法所需要的數據包括：①全部節點的坐標信息；②全部節點的唯一編號信息；③全部網格單元上的節點信息；④網格節點按逆時針排序信息。以上所有信息均由改進四叉樹算法進行存儲，以便后續調用。具體的操作如下：

（1）從單元樹中讀取所有未細化單元中的單元密度信息以及包含全部按逆序排序的節點編號信息。

（2）從節點樹中讀取所有節點位置信息與節點編號信息。

（3）通過式（15）計算獲得單元剛度矩陣并將其保存。

（4）結合步驟（1）中獲得的單元密度信息，依據式（16）計算獲得經過懲罰后的單元剛度矩陣。

（5）先對結構整體剛度矩陣進行組裝，后計算所有節點上的位移。

3? 數值案例和分析

本節通過兩個案例對ADD-SIMP與SIMP方法在計算時間、迭代次數、所用網格數、結構邊界的清晰度幾個方面進行了對比研究，并對其中主要參數的影響規律進行了分析，其中包含初始網格數量、細化閾值、過濾半徑。所有計算均在同一臺計算機上進行，計算機參數如表4所示。

3.1? 懸臂梁案例分析

如圖13所示，案例一為一個左端固支的懸臂梁，在右端最下角節點處施加外載荷為1 N的外力，懸臂梁的尺寸為120 mm×40 mm，彈性模量為1 MPa，泊松比為0.3。

SIMP方法的優化結果如圖14所示，當該方法獲得1 mm左右結構精度時，網格劃分至少應為480×160，網格數量為76 800個，單個網格尺寸為0.25 mm，此時受偽密度單元影響，結構邊界處的精度約為0.75 mm，優化后的結果如圖14a所示，計算時間為60 642 s（約17 h）。

ADD-SIMP方法的結果由不同等級網格單元組成，所有網格線均顯示，初始網格設置為120×40、初始網格尺寸為1 mm、最小網格單元等級為2、細化閾值設置為0.08的最終優化結果如圖15所示。最終所用網格總數為26 205，計算時間為711 s（約12 min），最小網格的尺寸為0.25 mm。

在保持原始結構比例不變的前提下，SIMP方法需要將設計區域劃分為270×90共24 300個網格，此時與ADD-SIMP方法所用網格數量相近。在270×90的結構中，每個網格的尺寸約為0.44 mm。SIMP方法最終的優化結果如圖14b所示，整個計算過程耗時為6644 s，是采用ADD-SIMP方法所需時間的9倍。SIMP方法的最小網格尺寸為采用ADD-SIMP方法時的兩倍左右，因此ADD-SIMP方法具有更優的邊界精度。

結合圖14和圖15可以看出，利用ADD-SIMP方法得到的最終結構與SIMP方法得到的120×40主結構相似（圖14c），隨著網格數量的增加，ADD-SIMP方法兼顧了270×90與480×160網格中的主要分支結構，減少了細小分支數量，具有更好的效果。

從圖16a中可以看出，SIMP方法優化結果中網格尺寸相同，結構中已穩定區域（實體單元和空白區域）充斥著大量的網格單元，但是對邊界處的精度并沒有貢獻，因此網格利用率低；相比之下，在圖16b所示的ADD-SIMP方法結果中，整體結構由三級尺寸不同的網格構成，已穩定區域的網格尺寸大且稀疏，結構邊界處網格尺寸小且密集。在ADD-SIMP方法中，結構邊界處的最小網格尺寸與SIMP方法中相同，因此兩者在邊界處的精度幾乎沒有差別。然而，ADD-SIMP方法在構建整體結構時所需的網格總數顯著少于SIMP方法所需的網格總數，表明ADD-SIMP方法在提高計算效率的同時保持了邊界精度，優化了網格的利用率。

從表5中可以看出，ADD-SIMP方法在達到相同精度水平時，最終所用的網格數量為26 205個，相較于SIMP方法在480×160結構所需的網格數量，ADD-SIMP方法僅用了其1/3的網格數量。兩種方法在針對結構最終目標函數的優化結果上相似，但是在邊界處精度相同的條件下，ADD-SIMP方法的計算效率顯著提高，可達到SIMP方法計算效率的85倍。此外，當與具有相似網格數量的SIMP方法相比時，ADD-SIMP方法的計算效率也有顯著提高，可達到原來的9倍。值得注意的是，在這種比較條件下，ADD-SIMP方法邊界處的精度提高至原來的兩倍。這些結果表明了ADD-SIMP方法在提高計算效率方面具有優勢。

3.2? 簡支梁

如圖17所示，案例二為一個兩端固支的簡支梁，在中點處施加外載荷為1N的外力，懸臂梁的尺寸為240 mm×40 mm，彈性模量為1 MPa，泊松比為0.3。

對于ADD-SIMP方法，初始網格劃分為120×20共2400個初始網格，最小網格單元等級設置為2，即最小網格的尺寸為0.5 mm，細化閾值設置為0.06；為保證相同精度，傳統SIMP的網格劃分應設置為480×80共38 400個網格。兩種方法的拓撲優化懲罰因子和過濾半徑均選取為3。ADD-SIMP方法經過30次迭代后的優化最終效果如圖18a所示。

ADD-SIMP方法計算所用時間為217.6 s（約0.06 h），SIMP方法經過201次迭代，所用時間為24 019.2 s（約6.67 h），ADD-SIMP方法的計算效率為原來的110倍，對于同樣迭代次數的SIMP方法，計算所用時間仍需要3584.9 s；在目標函數的優化上，ADD-SIMP方法的目標函數值小于SIMP方法的目標函數值；ADD-SIMP方法最終所用網格數量為15 231個，僅用原方法的1/2網格數量即可得到結構與精度相似的最終結構。

此外從圖18b中可以看出，SIMP方法得到的結果中細枝結構仍較多，ADD-SIMP方法得到的結構在一定程度上抑制了細小分支的出現。

3.3? 參數分析

3.3.1? 初始網格數量

對于ADD-SIMP方法，將初始網格劃分為30×10、60×20、120×40三組進行分析對比，如表6和表7所示。為保證最小網格單元尺寸相同，均設置為0.25 mm，因此上述三組的最小網格單元等級設置分別為4、3、2。

從表6中可以看出，三種初始網格劃分情況下所得到的最終網格數量均在26 000個左右，相對于原來的76 800個網格，所需網格數量僅為原來的1/3。

從表7中可以看出，初始網格數量為60×20的結構計算時間最短，為556.0 s（約9 min），時間僅為SIMP方法的1/109，計算效率提高了100倍以上；三組的目標函數值相近，SIMP方法最終目標函數值為182，因此使用ADD-SIMP方法可能導致目標函數值略微偏高；但是三種不同初始網格劃分的情況下，最終的目標函數值相差不大，可知初始網格數量對結構輕量化程度的影響較小；然而，初始網格數量對循環次數的影響顯著，計算時間會隨著初始網格數量的增加先減少后增加。

表8～表10分別展示了不同初始網格數量下結構的優化過程，可以看出，隨著初始網格數量由少變多，結構在第一次進行網格細化時所處狀態不同。初始網格過少時，一次細化的結構并未出現主承力結構，而是處于亂序狀態，直到后續網格數量增加才出現穩定的主承力結構，并趨向于穩定。當初始網格數量變多，結構首次細化時就

已經具有相對清晰的主承力結構，但是第一次細化所處的循環數也更大，進入第一次網格細化的時間會被延長。此外大量的初始網格數會直接增加計算負擔，最終導致計算時間變長。

從表8中還可以發現，當初始網格數量較少時，結構中出現的承力結構數量少、尺寸大，但是隨著后續網格數量的增加，結構有出現小分支的趨勢，因此ADD-SIMP方法在一定程度上具有減少結構細小分支的作用。

綜上可知，當初始網格數量選擇合適時，不僅可以大幅度縮短計算時間，還可以達到減少結構細小分支的效果。

3.3.2? 細化閾值

在ADD-SIMP方法中，細化閾值是作為網格細化策略的關鍵參數，用于決定何時對結構的網格進行細化。具體來說，該閾值設定了一個標準：只有當結構中網格單元的密度變化最大值不超過此閾值時，才會執行網格細化操作。由此可知，細化閾值的設定直接影響到拓撲優化過程中網格細化的時機。選擇合適的細化閾值是確保優化過程既高效又精確的關鍵因素。

在60×20的初始網格和最小單元等級為3的前提下，選擇細化閾值為0.06、0.08、0.1三個數值進行對比分析，如表11所示，可以看出，細化閾值設置取值越大，第一次進行網格細化時所處的循環數越小，則計算時間越短；但是細化閾值設置過大時可能導致結構主承力結構并未出現（如表12中0.1細化閾值下第一次細化結果），需要配合多次細化才能保證結果的準確性；若細化閾值取值偏小，則會延長結構進行細化的時間，從而降低計算效率；若細化閾值取值過小，甚至不會進入網格細化操作。

3.3.3? 過濾半徑

過濾半徑為SIMP方法中的主要影響參數之一，分別設計2、2.5、3、3.5、4五組過濾半徑，分析過濾半徑對ADD-SIMP方法的影響規律。對案例一初始網格數量的研究中，可以發現初始網格為60×20、細化閾值為0.08、最小網格單元等級設置為3的一組計算時間最短。

從表13中可以看出，隨著過濾半徑的增大，當過濾半徑為2.5～4之間時迭代次數先減少后增加，計算時間也是先增加后減少隨后又快速增加，最終網格數量整體呈現增加趨勢。

由于過濾半徑影響每次迭代中每個單元上的計算成本，則過濾半徑選擇過大會導致每個單元上靈敏度計算過濾的成本增加，但當過濾半徑為3左右時，迭代次數會減少，從而導致最終的計算時間縮短。此外由于過濾半徑內所有單元都會參與中心單元的靈敏度計算，因此導致過濾半徑內的每個單元都會獲得部分周圍實體單元的相對密度，從而導致邊界處的偽密度單元數量增加，進而影響ADD-SIMP方法細化后的網格數量。

從表14中可以看出，過濾半徑對最終結構會產生較大的影響，過濾半徑選擇較大時，靠近約束端的細小分支結構會被整合，同時偽密度單元數量會增加；當過濾半徑過小時，會具有更多的細小分支，但是邊界處的偽密度單元數量會減少。

4? 結論

對于大型結構拓撲優化方法計算成本高和固體各向同性材料懲罰模型（SIMP）方法在優化后結構邊界模糊的問題，通過改進四叉樹算法、比例邊界有限元法（SBFEM）和自定義細化網格的策略，本文提出了基于SIMP方法的自適應設計域（ADD）拓撲優化算法（以下簡稱“ADD-SIMP方法”），并對其中的參數設置進行了分析，在懸臂梁和簡支梁上進行了應用。從本文應用的案例中可得出如下結論：

（1）改進四叉樹算法通過定義細化策略可以實現在拓撲優化過程中對結構的邊界自動進行劃分網格操作，從而提高最終結構在邊界處的計算精度。

（2）若設置最小網格單元等級為2時，僅需要1/3左右的初始網格數量即可得到同邊界精度的優化結果。

（3）ADD-SIMP方法得到的結構分支較少，可制造性更高，在邊界處的平滑程度和精度與傳統方法相似。

（4）ADD-SIMP方法的在計算成本方面遠優于傳統方法，最終網格數量僅為原來的1/3，最快的計算速度效率是原始SIMP方法的100倍。

對于網格數量更多、結構更龐大、計算需要數天的大型結構，采用ADD-SIMP方法可以節省更多的計算資源、縮短設計周期。

參考文獻：

［1］? 郭西園， 衛鐘可， 杜建國， 等. 基于3D打印的減速箱體拓撲優化及應用［J］. 航天制造技術， 2022， 235（5）：59-61.

GUO Xiyuan， WEI Zhongke， DU Jianguo， et al. Topology Optimization and Application of Gearbox Based on 3D Printing［J］. Aerospace Manufacturing Technology， 2022， 235（5）：59-61.

［2］? 孟亮， 仲明哲， 李文彪， 等. 面向增材制造的航空發動機外部系統支架拓撲優化設計［J］. 中國機械工程， 2022， 33（23）：2822-2832.

MENG Liang， ZHONG Mingzhe， LI Wenbiao， et al. Topology Optimization Design of Aero-engine External System Brackets for Additive Manufacturing［J］. China Mechanical Engineering， 2022， 33（23）：2822-2832.

［3］? 梁健， 李曉杰， 謝炯. 拓撲優化在工業機器人造型設計中的應用［J］. 機械設計， 2020， 37（9）：128-133.

LIANG Jian， LI Xiaojie， XIE Jiong. Application of Topology Optimization in Industrial Robot Modeling Design［J］. Journal of Machine Design， 2020， 37（9）：128-133.

［4］? 朱鵬程， 楊志勛， 閻軍， 等. 基于拓撲優化方法的海洋柔性管纜限彎器新型設計研究［J］. 船舶力學， 2023， 27（3）：415-426.

ZHU Pengcheng， YANG Zhixun， YAN Jun， et al. New Configuration Design Methodology of Bend Restrictor of Marine Flexible Pipes and Cables Based on Topology Optimization［J］. Journal of Ship Mechanics， 2023， 27（3）：415-426.

［5］? 劉英杰， 胡強， 趙新明， 等. 汽車發動機連接支架拓撲優化及增材制造研究［J］. 中國機械工程， 2023， 34（18）：2238-2247

LIU Yingjie， HU Qiang， ZHAO Xinming， et al. Research on Topology Optimization and Additive Manufacturing of Automotive Engine Connection Brackets［J］. China Mechanical Engineering， 2023， 34（18）：2238-2247