基于嚴格反饋模型的電液伺服作動器控制策略研究

倪濤 呂博 張泮虹 趙澤仁 孫旭 張紅彥

摘要：

主動懸架可根據車輛實時狀態調節懸架參數，顯著提高應急救援車輛救援效率，電液伺服作動器是電液伺服主動懸架系統實施主動控制的核心部件。對電液伺服作動器控制策略展開了研究，建立了主動懸架液壓伺服作動器模型；基于該模型提出了基于嚴格反饋模型的自適應位置跟蹤控制策略，并證明了該策略在Lyapunov意義下的穩定性。仿真和單缸實驗驗證表明，與傳統控制方法相比，所提出的位置跟蹤算法可有效提高電液伺服作動器的位置跟蹤性能。

關鍵詞：三軸應急救援車輛；主動懸架；電液伺服作動器；位置跟蹤；自適應

中圖分類號：

DOI：10.3969/j.issn.1004132X.2024.05.018

開放科學（資源服務）標識碼（OSID）：

Research on Control Strategy of Electro-hydraulic Servo Actuators

Based on Strict Feedback Model

NI Tao1? LYU Bo1? ZHANG Panhong1? ZHAO Zeren1? SUN Xu1? ZHANG Hongyan2

1.School of Vehicle and Energy，Yanshan University，Qinhuangdao，Hebei，066000

2.College of Mechanical and Aerospace Engineering，Jilin University，Changchun，130022

Abstract： The active suspension might adjust the suspension parameters according to the real-time status of the vehicles， which greatly improved the rescue efficiency of emergency rescue vehicles. Electro-hydraulic servo actuator was the core component of active control of electro-hydraulic servo active suspension system， the control strategy of electro-hydraulic servo actuator was studied. The active suspension hydraulic servo actuator model was established. Then， based on the model， an adaptive position tracking control strategy was proposed based on a strict feedback model， and the stability of the proposed strategy in the Lyapunov sense was proved. The simulation and single-cylinder experiments show that the position tracking algorithm proposed may effectively improve the position tracking performance of electro-hydraulic servo actuators compared with the traditional control methods.

Key words： three-axis emergency rescue vehicle; active suspension; electro-hydraulic servo actuator; position tracking; adaptive

收稿日期：20230317

基金項目：河北省重點研發計劃（21351802D）；吉林省重點研發計劃（20200401130GX）

0? 引言

應急救援車輛作為災害應急救援的專用車輛［1］，在搶險救援中發揮著重要作用，因此要求應急救援車輛在惡劣的行駛條件下必須保持良好的行駛機動性、平順性和穩定性［2］。

懸架系統是連接車身與車輪的主要裝置，通常由彈性元件、減振器及導向機構等部件組成，是車輛底盤的重要組成部分［3］。傳統被動懸架系統因其懸架剛度和阻尼系數無法實時自動調整，嚴重制約其平順性和道路友好性的提升空間［4］。為解決現有應急救援車輛被動懸架系統存在的問題，人們提出了可自動調節阻尼和剛度的主動懸架系統，在面對復雜路面時，主動懸架系統可根據路面情況與車身狀況對各個車輪處的作動器進行調節，從而能夠有效降低由于路面凹凸不平所引起的車身起伏及振動［5］。

主動懸架性能不僅依賴執行器的類型，也與控制算法密切相關［6］，簡單有效、性能良好的控制算法一直是主動懸架開發的關鍵問題之一［7］，因此在將主動懸架系統應用于應急救援車輛的基礎上，還需針對執行機構設計有效的控制方法。目前廣泛應用于車輛主動懸架的作動器主要包括電控空氣彈簧、電磁致動器以及電液伺服作動器［8］。相比于空氣彈簧和電磁致動器，電液伺服作動器具有更大的承載能力以及更高的可靠性。考慮到本文所研究的三軸應急救援車輛具有承載大、質心高、行駛工況較復雜等特點，電液伺服作動器更切合應急救援車輛對主動懸架執行機構功能的需求。此外，電液伺服作動器可以進行快速響應和高精度伺服控制［9］。

電液伺服主動懸架系統主要由液壓泵、電液伺服閥、液壓缸等液壓元件及電控系統組成［10］。作為主動懸架系統實施主動控制的核心部件，其作動性能的好壞將直接影響車輛主動懸架系統的性能。PID控制雖然早在20世紀30年代就出現，但直到今天仍是各種工業控制領域應用最為普遍的閉環控制器［11］，由于PID控制結構簡單，參數調整方便，目前已廣泛應用于電液伺服系統的控制領域［12］。但常規的PID控制難以應對被控系統參數時變等情況，因此各國學者針對電液伺服控制系統的不同應用情況開發了多種先進的控制策略。在現有研究中，學者針對電液伺服作動器的跟蹤精度、時間滯后以及外部擾動等問題進行了分析，并設計了反步、自適應等控制器。但反步設計方法也存在著明顯的缺陷［13］，由于各種控制器的實現都是基于模型設計的，因此若模型過于簡潔，雖然可以使控制器設計過程變得簡單，但卻會影響系統實際工作時的控制效果。若考慮復雜高階的模型，則所設計的控制器性能優異，但難以工程實現，因此需對電液伺服作動器模型進行進一步研究。

本文建立了電液伺服作動器的非線性模型，介紹了相關控制理論及引理和假設；針對具有非線性特性以及外部擾動的電液伺服作動器，研究了高精度的位置跟蹤策略，提出了一種嚴格反饋模型，在此基礎上設計了滑模自適應控制器，解決了模型中存在不確定參數和擾動的問題，并利用Lyapunov穩定性理論證明所設計控制器的穩定性；通過仿真進行驗證，并在電液伺服作動器試驗臺進行試驗，驗證了所設計的控制方法在實際應用中的控制效果。

1? 系統模型分析

三軸應急救援車輛底盤空間較為緊湊，采用閥控單出桿液壓缸作為主動懸架系統的執行機構，圖1所示為電液伺服作動器模型，作動器通過調節伺服閥的開度控制油液流入上下腔并調節其流量，通過改變上下腔的壓力產生壓力差，推動液壓缸上下移動，從而調整作動器位移Xs，同時輸出相應主動力。圖1中m為質量塊質量，Din為無桿腔內徑，dr為桿直徑，u為控制閥芯移動的輸入電壓；當伺服閥的開度｜Xv｜大于0時，液壓油通過供油管路流入無桿腔，供油壓力為ps，伺服閥開度控制無桿腔流量q1以及無桿腔壓力p1，同時有桿腔與回油管路相連，回油壓力為pr，有桿腔內油液進行回流，此時有桿腔內流量為q1且其壓力為p2；當｜Xv｜小于0時，有桿腔與供油管路相連，伺服閥開度控制有桿腔流量q2及有桿腔壓力p2，同時無桿腔與回油管路相連；當｜Xv｜為0時，流量通道切斷，兩腔壓力保持穩定不變。

定義上下腔的進油與回油流量方程為

q1=cdW｜Xv｜2（ps－p1）/ρ? ｜Xv｜≥0

cdW｜Xv｜2（p1－pr）/ρ｜Xv｜<0（1）

q2=cdW｜Xv｜2（p2－pr）/ρ? ｜Xv｜≥0

cdW｜Xv｜2（ps－p2）/ρ｜Xv｜<0（2）

式中，W為伺服閥面積梯度；cd為閥芯控制口流量系數；ρ為油液密度。

令

kq=cdW2ρ（3）

引入s（x）函數：

s（x）=1? x≥0

0x<0（4）

則流量方程可表示為

q1=kqs（Xv）｜Xv｜（s（Xv）ps－p1+

s（－Xv）（p1－pr）（5）

q2=kqs（Xv）｜Xv｜（s（Xv）p2－pr+

s（－Xv）ps－p2）（6）

定義因上下兩腔壓力差而在活塞間隙處產生的內泄漏流量為

q11=Ct（p1－p2）（7）

式中，Ct為液壓缸內泄漏系數。

定義液壓缸頭部與活塞桿之間的縫隙處產生的外泄漏流量為

q12=Cpp2（8）

式中，Cp為液壓缸外泄漏系數。

定義因上下兩腔壓力的動態變化而產生的流量變化分別為

q13=p·1Vh1+A1｜Xs｜β（9）

q14=p·2Vh2－A2｜Xs｜β（10）

式中，Vh1+A1｜Xs｜、Vh2－A2｜Xs｜分別為上下兩腔因活塞上下移動而產生的容積變化；Vh1、Vh2分別為無桿腔初始容積和有桿腔初始容積；A1、A2分別為無桿腔截面積和有桿腔截面積；β為油液彈性模量。

根據流量守恒定律，由式（1）～式（10）可得到有關液壓缸上下兩腔壓力的動態變化方程分別為

q1=A1｜X·s｜+Ct（p1－p2）+p·1Vh1+A1｜Xs｜β（11）

q2=A2｜X·s｜+Ct（p1－p2）－

Cpp2－p·2Vh2－A2｜Xs｜β（12）

式中，A1｜X·s｜、A2｜X·s｜分別為作動器上下兩腔因活塞位移改變而產生的流量變化。

根據牛頓第二定律及液壓缸的工作原理，可得到圖1中的動力學方程為

m｜X¨s｜=（A1p1－A2p2）－b｜X·s｜+

｜FL（Xs，X·s，X¨s，t）｜（13）

式中，b為油液的黏性阻尼系數；FL為液壓伺服作動器的外部干擾；t為時間。

至此，得到主動懸架液壓伺服作動器的動力學模型，包括液壓缸上下腔壓力的動態方程，以及由于腔內壓力變化產生對外主動力時所得到的外部的力平衡方程。

為使所設計的控制策略便于讀者理解，下面給出本文在設計控制策略以及穩定性分析時所需要的假設與引理。

假設1? 假設作動器的期望位移上下有界，且其多階導數同樣有界。

假設2? 設計控制器時，所提到的參數θi（i=1，2，3，4，5）都為正值且有界［14］。

假設3? 若存在未知常數D≥0和已知非負光滑函數φ（x，t）：R3×R+→R，x∈R3，t∈R+，則外負載擾動dL滿足｜dL（x，t）｜≤Dφ（x，t）［15］。

引理1? 對于ε>0，η∈R，存在0≤｜η｜－ηtanh（η/ε）≤kε，且k=exp（－（k+1））≈0.2785［16］。

引理2? 假設a′、b′為非負實數，1c′+1d′=1，則a′b′≤（a′）c′c′+（b′）d′d′，且僅當（a′）c′=（b′）d′時，等號成立，此為楊氏不等式的一般形式。

引理3? 在現代控制理論中，Lyapunov第二法是穩定性分析的常用方法，因此本文利用第二法進行系統的穩定性分析。

引理4? ?變結構控制理論是系統可以根據當前狀態自動改變控制輸入的結構。

2? 基于嚴格反饋模型的自適應位置跟蹤控制

圖2為系統的整體控制框圖。定義模型中的四個狀態變量，形式為x1= ｜Xs｜，x2= ｜X·s｜，x3=p1，x4=p2，由此可導出液壓伺服作動器的狀態空間方程為

x·1=x2

x·2=－θ1x2+θ2（A1x3－A2x4）+dL

x·3=f31（x1，x2）θ3+f32（x1，x3，x4）θ4+

g3（x1，x3，Xv）θ5｜Xv｜

x·4=f41（x1，x2）θ3+f42（x1，x3，x4）θ4+

g4（x1，x4，Xv）θ5｜Xv｜（14）

θ1=b/m? θ2=1/m? θ3=β? θ4=βCt

θ5=βg? dL=｜FL｜/m

f31（x1，x2）=－A1x2Vh1+A1x1

f32（x1，x3，x4）=x4－x3Vh1+A1x1

f41（x1，x2）=A2x2Vh2－A2x1

f42（x1，x3，x4）=x3－x4Vh2－A2x1

g3（x1，x3，Xv）=

s（Xv）ps－x3+s（－Xv）x3－prVh1+A1x1

g4（x1，x4，Xv）=

－（s（Xv）x4－pr+s（－Xv）ps－x4）Vh2－A2x1

其中，g為重力加速度，s（Xv）在式（4）中已給出其具體形式。

引入x-3=p1－p2A2/A1作為新的狀態空間變量，則系統的狀態空間方程可改寫為

x·1=x2

x·2=－θ1x2+θ2A1x-3+dL

x·-3=（f31（x1，x2）－f41（x1，x2）A2/A1）θ3+

（f32（x1，x3，x4）－f42（x1，x3，x4）A2/A1）θ4+

（g3（x1，x3，Xv）－g4（x1，x4，Xv）A2/A1）θ5｜Xv｜（15）

其中，x-3為液壓伺服作動器的等效負載壓力。

本文提出一種嚴格反饋結構，將模型中狀態變量直接用于控制設計，具體形式如下：

x·1=x2

x·2=－θ1x2+θ2｜μT2ζ｜+dL

ζ·=f34（X）（θ3，θ4）T+μ34（X，Xv）θ5Xv（16）

μ34（X，Xv）=（g3（x1，x2，Xv），g4（x1，x2，Xv））T

μ2=（A1，－A2）T? ζ=（x3，x4）T

f34（X）=f31f32f41f42

根據第1節的模型分析，可將g3和g4兩個函數分為以下三種形式：

（1）Xv>0時，g3（x1，x3，Xv）=ps－x3Vh1+A1x1，g4（x1，x4，Xv）=－x4－prVh2－A2x1；

（2）Xv<0時，g3（x1，x3，Xv）=x3－prVh1+A1x1，g4（x1，x4，Xv）=－ps－x4Vh2－A2x1，因此當Xv≠0時，g3和g4兩個函數可進行簡化；

（3）Xv=0時，相當于系統的過渡階段，在系統過渡階段，由式（14）可知x3、x4、dL和θ2均有界，且θ1大于零，此時系統變為關于作動器位移的二階系統。

在上述嚴格反饋模型的基礎上設計自適應位置跟蹤控制器，首先定義狀態誤差變量：

e1=x1－x1r

e2=x2－x·1r

e3=｜ζ－α｜（17）

式中，x1r為期望位移；α為虛擬控制變量；e1、e2、e3為誤差變量。

由式（17）得到誤差變量的導數為

e·1=x·1－x·1r

e·2=x·2－x¨1r

e·3=｜ζ·－α·｜（18）

定義不確定參數的估計誤差變量為

θ～i=θi－θ^i

D～=D－D^（19）

式中，θ^i、D^分別為參數θi、D的估計值。

針對控制算法選取合適的滑模面：

s1=ce1+e2（20）

其中，c為正常數，則該滑模面的導數為

s·1=ce·1+e·2=c（x·1－x·1r）+

（－θ1x2+θ2｜μT2ζ｜+dL）－x¨1r（21）

然后通過多次選取合適的Lyapunov函數，逐步解算出中間過程的虛擬控制變量，再推出系統的最終控制輸入。所選取Lyapunov方程為

V1=12s21+12λ1θ～21+12λ2θ～22+12λDD～2（22）

其中，λ1、λ2、λD為正常數，則V1的導數為

V·1=s1s·1－1λ1θ～1θ·^? 1－1λ2θ～2θ·^? 2－1λDD～D·^? =

（ce·1+e·2）－1λ1θ～1θ·^? 1－1λ2θ～2θ·^? 2－1λDD～D·^? =

s1（ce2－θ1x2+θ2｜μT2ζ｜+dL－x¨1r）－

1λ1θ～1θ·^? 1－1λ2θ～2θ·^? 2－1λDD～D·^? ≤s1（ce2－θ1x2+

θ2｜μT2ζ｜－x¨1r）+s1Dφ（x，t）tanh（s1φ（x，t）/ε）+

kDε－1λ1θ～1θ·^? 1－1λ2θ～2θ·^? 2－1λDD～D·^? （23）

其中，ε、k均為正常數，且由假設3及引理1知其滿足：

ε=ε0/D（24）

η=s1dL（25）

s1dL≤s1Dφ（x，t）tanh（s1φ（x，t）/ε）+kDε（26）

由給出的Lyapunov方程及其導數，可得出自適應參數的方程以及虛擬控制變量為

θ·^? 1=－λ1s1x2－λ1γ1（θ^1-θ10）

θ·^? 2=λ2s1｜μT2ζ｜－λ2γ2（θ^2-θ20）

D·^? =λDs1φ（x，t）tanh（s1φ（x，t）/ε）－λDγD（D^-D0）（27）

α=（A1/（A21+A22），－A2/（A21+A22））T（1/θ^2）·

［－k1s1－ce2+θ^1x2+x¨1r－

D^φ（x，t）（tanh（s1φ（x，t）/ε）］（28）

其中，γ1、γ2、γD、k1均為正常數，θ10、θ20、D0分別為對應參數的初始值。

根據楊氏不等式，可得

θ～i（θ^i－θi0）≤－θ～2i/2+（θ^i－θi0）2/2? i=1，2

D～（D^－D0）≤－D～2/2+（D^－D0）2/2

（29）

將式（24）～式（29）代入式（23）可得

V·1≤V－·1+s1θ^2｜μT2e3｜+Ω1（30）

V－·1=－k1s21－∑2i=1γiθ～2i/2－γDD～2/2<0

Ω1=

γ1（θ^1－θ10）2+γ2（θ^2－θ20）2+γD（D^－D0）22+kDε

為得到自適應參數θ3、θ4、θ5的最終控制輸入，需再次選取Lyapunov函數：

V2=V1+12｜eT3e3｜+12λ3θ～23+12λ4θ～24+12λ5θ～25（31）

其中，λ3、λ4、λ5均為正常數，則V2的導數為

V·2=V·1+｜eT3e·3｜－1λ3θ～3θ·^? 3－1λ4θ～4θ·^? 4－1λ5θ～5θ·^? 5≤

V－·1+s1｜θ^2μT2e3｜+｜eT3（f34（X）（θ3，θ4）T+

μ34（X，Xv）θ5Xv－α·）｜－1λ3θ～3θ·^? 3－1λ4θ～4θ·^? 4－

1λ5θ～5θ·^? 5+Ω1（32）

至此，可推導出其他參數的自適應律以及作動器閥芯位移的最終控制輸入如下：

θ·^? 3=｜λ3（f31，f41）e3｜－λ3γ3（θ^3-θ30）

θ·^? 4=｜λ4（f32，f42）e3｜－λ4γ4（θ^4-θ40）

θ·^? 5=｜λ5eT3μ34（X，Xv）Xv｜－λ5γ5（θ^5-θ50）（33）

Xv=（－k2eT3e3－s1θ^2μT2e3+eT3α·－

eT3f34（X）（θ^3，θ^4）T）/（eT3μ34（X，Xv）θ^5）（34）

其中，γ3、γ4、γ5、k2均為正常數，θ30、θ40、θ50分別為對應參數初始值。

同上，根據楊氏不等式，可得以下公式：

θ～i（θ^i－θi0）≤－θ～2i/2+（θ^i－θi0）2/2 （35）

i=3，4，5

將式（33）～式（35）代入式（32）可得

V·2≤V－·1－k2｜eT3e3｜+∑5i=3γiθ～i（θ^i－θi0）+

Ω1≤－k2｜eT3e3｜－k1s21－∑5i=1γiθ～2i/2－

γDD～2/2+Ω2≤V－·2+Ω2（36）

V－·2=－k2｜eT3e3｜－k1s21－∑5i=1γiθ～2i/2－

γDD～2/2<0

Ω2=

12∑5i=1γi（θ^i－θi0）2+12γD（D^－D0）2+kDε

其中，參數k1、k2影響系統的跟蹤性能和控制響應的抖動，λi（i=1，2，…，5）、λD、γi（i=1，2，…，5）、γD影響參數估計的收斂速度。

由選定的Lyapunov函數可知V2>0，假設

c1=max{12，12λi12λD}? i=1，2，…，5

c2=min{k1，k2，λD2，λi2}? i=1，2，…，5

則由式（31）和式（36）可進行以下推導：

V2≤c1（s21+｜eT3e3｜+∑5i=1θ～2i+D～2）（37）

V·2≤－k2｜eT3e3｜－k1s21－∑5i=1γiθ～2i/2－γDD～2/2+

Ω2≤－c2（｜eT3e3｜+s21+∑5i=1θ～2i+D～2）+Ω2（38）

進而得到有關V2導數的不等式如下：

V·2≤－c2c1V2+Ω2（39）

對式（39）等號兩邊同時乘以exp（tc2/c1）并積分，可得

V2（t）≤V2（0）exp（-tc2/c1）+Ω2/（c2/c1）－（Ω2（0）+

∫t0exp（tc2/c1）dtΩ2）exp（-tc2/c1）/（c2/c1）（40）

又由于當t≥0時，exp（tc2/c1）≥1，因此可得到：

V2（t）≤Ω2（1－exp（-tc2/c1））/（c2/c1）+

V2（0）exp（-tc2/c1）（41）

由式（41）可得，當t→∞時，ei（i=1，2，3）、θ～i和D～收斂到Ω2/（c2/c1）。根據假設1，由于期望位移與其多階導數均有界，以及誤差ei（i=1，2，3）收斂，可得系統的狀態變量xi（i=1，2，3，4）有界。同理根據假設2和假設3，可得不確定參數的估計值θ^i（i=1，2，…，5）有界，估計值D～有界。最后Ω2/（c2/c1）可通過調整各個控制增益的大小而減小到任意值。

該自適應控制方法與以往研究中常用的投影算子控制方法有所不同，可通過自適應法則在線估計外部負載擾動的未知邊界和作動器模型中的不確定參數，從而消除了由于參數不確定性和負載擾動而引起的不良影響，提高了液壓伺服作動器的輸出跟蹤性能。

3? 仿真分析

根據表1進行MATLAB/Simulink仿真分析。仿真中，參考位移選擇幅值為0.05 m，并根據實驗室所提供作動器的性能指標選擇頻率分別為0.5 Hz、1 Hz和2 Hz的正弦信號，三種控制方法的軌跡跟蹤對比結果如圖3～圖5所示。

作動器初始位置同為-0.05 m，將控制方法的自適應參數取值k1=1000、k2=15、c=20、γ1=γ2=γ3=γ4=γ5=0.001、γD=0.3、λ1=0.1、λ2=1×10-9、λ3=0.01、λ4=1×10-15、λ5=1×10-15、λD=1作為參考。

作動器在基于嚴格反饋模型的自適應控制方法、滑模自適應控制方法以及反步自適應控制方法下，跟蹤位移誤差的標準差如表2所示。通過仿真可知，不同頻率下，基于嚴格反饋模型的自適

應控制方法與滑模自適應控制方法相比，其跟蹤速度較快且跟蹤精度較高，與反步自適應控制方法相比，其跟蹤精度較高。

仿真中，參考位移的頻率均選取1 Hz的正弦信號，且正弦信號的幅值分別選擇0.05 m、0.08 m和0.1 m，三種控制方法的軌跡跟蹤對比結果如圖4、圖6、圖7所示。

在不同幅值下均可得到以下結論：基于嚴格反饋模型的自適應控制方法與滑模自適應控制方法相比，具有較好的跟蹤速度與精度，與反步自適應控制方法相比，具有較好的跟蹤精度。

綜合分析可知，在選取的參考位移的幅值和頻率發生變化時，本文所提出的控制方法與一般的控制方法相比，能以較快的速度與較高的精度進行位置跟蹤運動。

4? 試驗平臺搭建與試驗測試研究

本文試驗測試研究主要為電液伺服位置跟蹤控制試驗，采用了對比試驗方法，將實時采集的相應試驗數據進行標準量化及對比分析。

期望值μ的標準差為

σ=1N∑Ni=1（di－μ）2（42）

式中，di為采集到的第i個數據；N為采集到的數據數量。

誤差絕對值的最大值為

Md=maxi=1，2，…，N{｜di－μ｜}（43）

式中，di－μ表示期望值與實際值的誤差。

試驗數據的峰峰值為

MX=maxi=1，2，…，N{Xi}+mini=1，2，…，N{Xi}（44）

式中，maxi=1，2，…，N{Xi}表示試驗數據中的最大值；mini=1，2，…，N{Xi}表示試驗數據中的最小值。

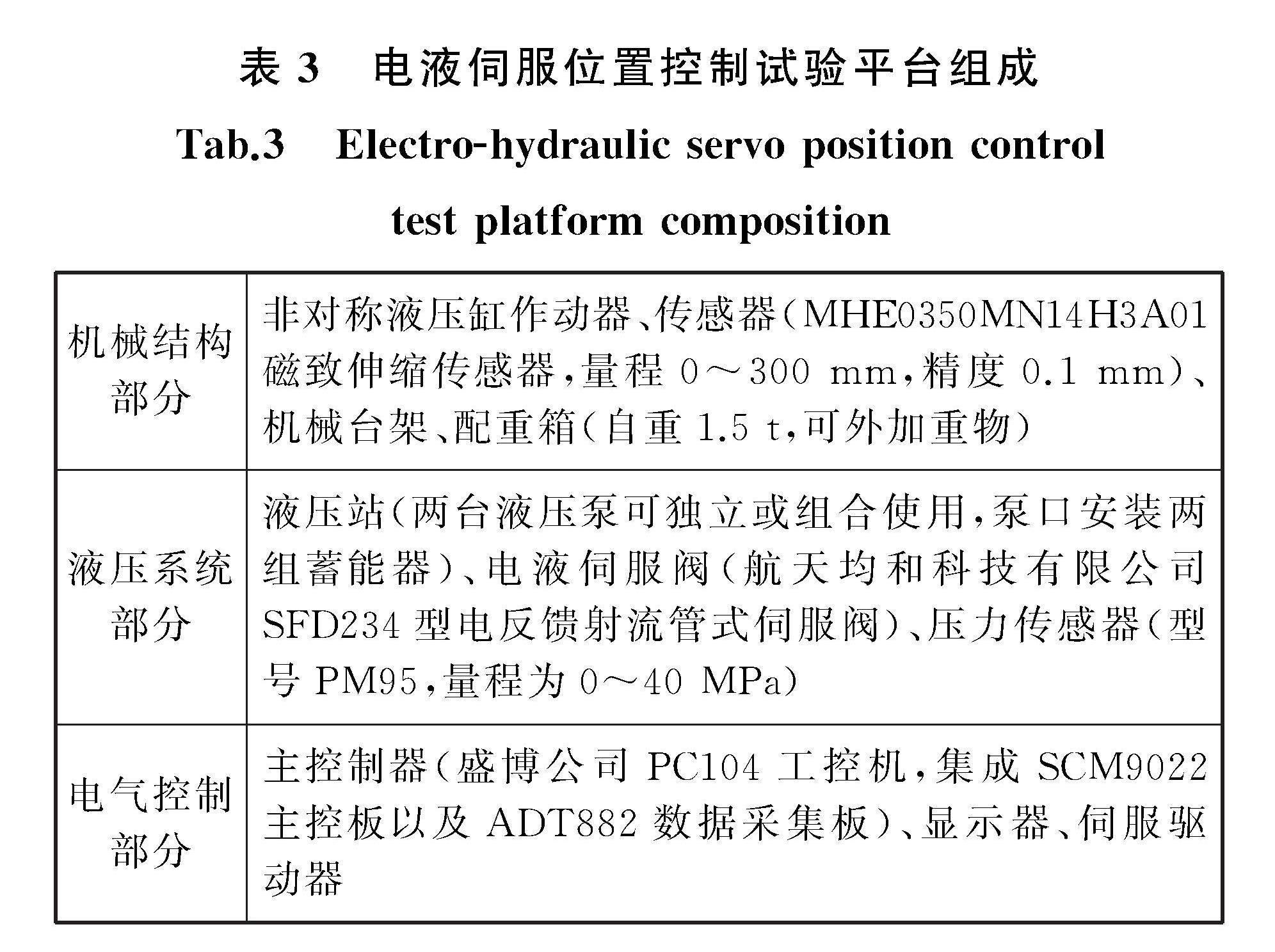
電液伺服位置控制試驗平臺包括機械結構部分、液壓系統部分以及電氣控制部分，具體組成見表3。

閥控缸位置控制系統原理如圖8所示，其中主控板與顯示器連接，用于控制算法的程序編寫

與實時控制。數據采集板與伺服驅動器連接，實現各傳感器信號的實時采集以及電液伺服閥的電流驅動，整體結構如圖9所示。

利用搭建的試驗平臺驗證本文所提出的電液伺服系統位置跟蹤控制方法的控制效果。分別選取不同頻率以及不同幅值的正弦信號作為系統跟蹤輸入，并同時采用基于嚴格反饋模型的自適應位置跟蹤控制方法和傳統PID方法進行對比試驗，最后采集試驗數據來對結果進行對比分析。控制算法程序在PC104工控機上編寫，周期為2 ms，PID控制算法的參數如下：比例系數為60，積分系數為0.1。基于嚴格反饋模型的自適應位置跟蹤控制方法參數如下：k1=1×104、k2=155、c=100、γ1=γ2=γ3=γ4=γ5=0.001、γD=0.3、λ1=0.1、λ2=1×10-7、λ3=0.1、λ4=1×10-10、λ5=1×10-10、λD=1。

如圖10～圖12所示，當幅值相同時三種頻率下自適應控制方法的正弦跟蹤誤差均小于PID控制的正弦跟蹤誤差，頻率越高，兩種方法的跟蹤誤差相差越明顯。對正弦跟蹤誤差的絕對值最大值進行量化對比，見表4。由表4可知，在幅值為0.1 m，頻率分別為0.25 Hz、0.33 Hz和 0.5 Hz的輸入下，基于嚴格反饋模型的自適應位置跟蹤控制與傳統PID控制的位置跟蹤誤差的絕對值最大值相比，可得所提自適應控制方法的跟蹤性能分別提高了9.1%、25%和25.9%。

由圖10～圖12的位置跟蹤曲線可以看出，隨著控制頻率的提高，兩種控制方法的跟蹤誤差隨著時間歷程而遞增，原因為液壓系統提供的流量和壓力不足以支撐快速響應的電液伺服位置控制。由此，將幅值適當減小到0.06 m，同時提高頻率，再次試驗。

由圖13和圖14可以看出，當減小正弦跟蹤輸入幅值到0.06 m且提高頻率時，基于嚴格反饋模型的自適應控制的正弦跟蹤誤差仍小于傳統

PID控制的正弦跟蹤誤差。且由圖12、圖13及表4可以分析得出，在頻率為0.5 Hz，幅值分別為0.06 m、0.1 m的正弦跟蹤輸入下，本文提出的位置跟蹤控制方法相較于傳統PID控制，在跟蹤性能上分別提高了21.4%、25.9%，即對于不同幅值、相同頻率的正弦跟蹤控制，基于嚴格反饋模型的自適應控制方法仍可表現出較好的跟蹤性能。

5? 結論

本文對電液伺服主動懸架系統中的電液伺服作動器進行了深入研究，并取得以下創新性成果：針對PID控制無法有效應對電液伺服作動器系統的時變參數問題，提出了基于嚴格反饋模型的自適應位置跟蹤控制方法。建立了與常規模型不同的嚴格反饋模型，該模型可有效避免模型降階問題。并在此基礎上提出了自適應控制方法，解決了系統的時變參數問題。最后通過仿真與試驗驗證其控制效果。

參考文獻：

［1］? 高路路， 馬飛， 周志鴻， 等. 應急救援車輛產品概況［J］. 鑿巖機械氣動工具， 2017（1）：52-61.

GAO Lulu， MA Fei， ZHOU Zhihong， et al. Product Overview of Emergency Rescue Vehicles［J］. Rock Drilling Machinery and Pneumatic Tools， 2017（1）：52-61.

［2］? 劉清河， 和題， 劉燕寧. 搶險救援車技術現狀分析及展望［J］. 中國應急救援， 2010（5）：16-17.

LIU Qinghe， HE Ti， LIU Yanning. Analysis and Prospect of Rescue Vehicle Technology Status［J］. China Emergency Rescue， 2010（5）：16-17.

［3］? 陳家瑞. 汽車構造［M］. 北京：機械工業出版社， 2011：12-13.

CHEN Jiarui. Automobile Structure［M］. Beijing：China Machine Press， 2011：12-13.

［4］? 嚴天一，任坤儒，王玉林， 等. 車輛半主動懸架系統模糊混合控制策略［J］.農業機械學報，2012，43（12）：11-15.

YAN Tianyi， REN Kunru， WANG Yulin， et al. Fuzzy Hybrid Control Strategy of Semi-active Suspensions for Vehicle［J］.Transactions of the Chinese Society for Agricultural Machinery，2012，43（12）：11-15.

［5］? 陳浩， 鞏明德， 趙丁選， 等. 電液主動懸架靈敏度分析與自適應跟蹤控制［J］. 中國機械工程， 2023， 34（4）：481-489.

CHEN Hao， GONG Mingde， ZHAO Dingxuan， et al. Sensitivity Analysis and Adaptive Tracking Control of Electro-hydraulic Active Suspensions［J］. China Mechanical Engineering， 2023， 34（4）：481-489.

［6］? 王剛，周知進，陳海虹.車輛主動懸架免模型輸出反饋控制器設計與實驗［J］.農業機械學報， 2019，50（7）：389-397.

WANG Gang，ZHOU Zhijin，CHEN Haihong.Design and Experiment of Model-free Output-feedback Control for Vehicle Active Suspensions［J］.Transactions of the Chinese Society for Agricultural Machinery，2019，50（7）：389-397.

［7］? 寇發榮，許家楠， 劉大鵬， 等. 電動靜液壓主動懸架雙滑模控制研究［J］. 中國機械工程， 2019， 30（5）：542-548.

KOU Farong， XU Jianan， LIU Dapeng， et al. Study on Dual Sliding Mode Control of EHA Active Suspensions［J］. China Mechanical Engineering， 2019， 30（5）：542-548.

［8］? 寇發榮， 方宗德. 汽車可控懸架系統的研究進展［J］. 汽車工程， 2007， 29（5）：426-432.

KOU Farong， FANG Zongde. Research Progress of Automotive Controllable Suspension System［J］. Automotive Engineering， 2007， 29（5）：426-432.

［9］? 鄧樂. 液壓傳動［M］. 北京：北京郵電大學出版社， 2010：4-6.

DENG Le. Hydraulic Transmission［M］. Beijing：Beijing University of Posts and Telecommunications Press， 2010：4-6.

［10］? 郭慶賀. 多軸應急救援車輛電液伺服主動懸架控制策略研究［D］. 秦皇島：燕山大學， 2021.

GUO Qinghe. Research on Electro-hydraulic Servo Active Suspension Control Strategy of Multi-axis Emergency Rescue Vehicle［D］. Qinhuangdao：Yanshan University， 2021.

［11］? 楊慧勇.基于PID控制器的半主動懸架聯合仿真分析［J］.汽車實用技術，2023，48（4）：107-111.

YANG Huiyong. Co-simulation Analysis of Semi-active Suspension Based on PID Controller［J］.Automotive Practical Technology，2023，48（4）：107-111.

［12］? 吳宏鑫， 沈少萍. PID控制的應用與理論依據［J］. 控制工程， 2003（1）：37-42.WU Hongxin， SHEN Shaoping. Application and Theoretical Basis of PID Control［J］. Control Engineering， 2003（1）：37-42.

［13］? 袁朝輝，袁鳴.電液系統中新型反步自適應控制器設計［J］.機電工程，2013，30（7）：769-773.

YUAN Chaohui，YUAN Ming. Design of New Backstep Adaptive Controller in Electro-hydraulic System［J］.Electromechanical Engineering，2013，30（7）：769-773.

［14］? ZHANG Z， DUAN G， HOU M. Robust Adaptive Dynamic Surface Control of Uncertain Non-linear Systems with Output Constraints［J］. IET Control Theory and Applications， 2017， 11：110-121.

［15］? POLYCARPOU M M， IOANNOU P A. A Robust Adaptive Nonlinear Control Design［J］. Automatica， 1996， 32：423-427.

［16］? 齊曉慧. “李雅普諾夫穩定性理論”的教學研究［J］. 電力系統及其自動化學報， 2005， 17（3）：91-94.

QI Xiaohui. Teaching and Research on “Lyapunov Stability Theory”［J］. Transactions of the Chinese Society for Electric Power Systems and Automation， 2005， 17（3）：91-94.

（編輯? 胡佳慧）

作者簡介：

倪? 濤，男，1978 年生，教授、博士研究生導師。研究方向為遙操作、虛擬現實和機器人技術。E-mail：nitao@ jlu.edu.cn。

張紅彥（通信作者），女，1973 年生，副教授。研究方向為智能車輛。E-mail：zhanghy@jlu.edu.cn。