基于功率微分項的雙VSG有功功率振蕩抑制策略

摘"要：

針對虛擬同步發電機（VSG）雙機并聯運行時產生的有功功率振蕩問題，通過建立雙VSG系統的小信號模型，分析了有功功率振蕩產生的機理，提出一種基于改進虛擬阻抗的瞬態功率均分策略和一種基于功率微分項的自適應慣量和阻尼的功率振蕩抑制策略，將有功功率微分項與角加速度結合起來實現慣量的自適應調節，同時將有功功率微分項引入阻尼控制環節以替代傳統的阻尼項，實現阻尼的自適應調節。所提出的策略可以使動態時VSG之間的角頻率差更快速地趨近于零，從而減小有功功率振蕩的超調，改善頻率動態響應性能。搭建了VSG并聯的仿真模型，仿真結果表明：所提改進控制策略可以使瞬態時實現有功均分，使動態時的有功功率振蕩超調減小41%，振蕩過程減小了1秒。

關鍵詞：虛擬同步發電機;功率微分項；自適應慣量；阻尼；功率振蕩抑制；功率均分

DOI：10.15938/j.emc.2024.01.017

中圖分類號：TM46

文獻標志碼：A

文章編號：1007-449X（2024）01-0177-12

Active power oscillation suppression strategy for dualVSG grid based on power differential term

ZHU Jun1，nbsp;YUAN Yafei1，"LIU Penghui1，"DU Shaotong1，"GUO Xiangwei1，"YANG Ming1，"QU Yubo2

（1.School of Electrical Engineering and Automation， Henan Polytechnic University， Jiaozuo 454000， China; 2.XJ Electric Co.， Ltd，Xuchang 461000，China）

Abstract：

Aiming at the active power oscillation problem generated when the virtual synchronous generator （VSG） is operated in parallel， the mechanism of active power oscillation was analyzed by establishing a smallsignal model of the dual VSG system， and a transient power equalization strategy based on the improved virtual impedance and a power oscillation suppression strategy based on the power differential term with adaptive inertia and damping were proposed to realize the combination of the active power differential term with angular acceleration to achieve the adaptive regulation of inertia， while the active power differential term was introduced into the damping control link to replace the conventional damping term to realize the adaptive regulation of damping. The proposed strategy can make the angular frequency difference between the VSGs converge to zero more quickly during the dynamic time， so as to reduce the overshoot of the active power oscillation and improve the frequency dynamic response performance. A simulation model of VSGs connected in parallel was constructed， and the simulation results show that the proposed improved control strategy can realize active equalization in transient state， reduce the overshoot of active power oscillation by 41% and the oscillation process by 1 second in dynamic state.

Keywords：virtual synchronous generator; power derivative term; adaptive inertia; damping; power oscillation suppression; power sharing

0"引"言

目前，為了擺脫對傳統化石能源的依賴，以風、光為代表的分布式新能源發電技術得到了廣泛的關注。分布式電源通常以逆變器作為接口向電網或負載進行供電，考慮到風、光等新能源出力具有間歇性和波動性，對負載或電網來說其供電可靠性和可調度性較差，因此通常將一定區域內的多種新能源，負荷，儲能和保護裝置等組成一個具有自治能力的微電網[1-4]，以增強其可靠性和可調度性，從而達到新能源的最大利用率。

微電網內部的分布式電源通常以逆變器為接口向系統饋電，因此逆變器的控制方式便尤為重要，常用的控制方式有PQ控制，V/F控制，下垂控制等。在以同步發電機供電為主的電網中，系統有足夠的慣量與阻尼抵抗外界擾動，但是在以新能源供電為主的電網，上述常用的逆變器控制方式不能為系統提供慣量與阻尼，此時系統呈現若弱慣性和弱阻尼的特性，任何微小的擾動都可能使系統發生振蕩甚至失穩[5]。這嚴重制約了新能源并網發電的規模。近年來，有學者提出虛擬同步發電機（virtual synchronous generator，VSG）技術[6-8]，通過在逆變器的控制器中引入同步發電機（synchronous generator，SG）的二階轉子運動方程使逆變器具有與同步發電機等效的慣量與阻尼，這一技術較好地解決了大規模新能源并網所造成的慣量與阻尼缺失的問題，有望成為以逆變器為接口的分布式電源的主流接入方式。

VSG技術已經成為近年來的研究熱點，文獻[9]對VSG的基本原理、拓撲、穩定性分析方法、未來的研究方向以及應用做了全面的綜述。文獻[10-11]基于VSG的小信號模型進行了穩定性分析，給出了具體的參數設計指標。轉子運動方程的引入使VSG具有了慣量與阻尼特性，同時也引入了同步發電機固有的功率振蕩問題。當VSG工作在并網模式時，指令功率或電網頻率出現擾動時，VSG會出現較大的動態功率振蕩和超調。針對此問題，文獻[12]提出了一種基于電網頻率前饋的改進控制方法，在消除有功功率振蕩的同時，保持良好的穩態性能。但所提控制方法需要鎖相環測量電網頻率，增加了系統的建設成本。文獻[13]提出了一種帶通阻尼功率的改進策略，通過在阻尼項中增加帶通濾波器，在動態時提供較大的阻尼功率以抑制功率振蕩。文獻[14]針對VSG并網PQ運行時，固定慣量與阻尼參數無法兼顧穩態與動態特性的要求的問題，提出在輸出角頻率上疊加其微分量，從而增大動態過程中的系統阻尼，減小了擾動后的有功振蕩超調，且微分環節不影響穩態性能。文獻[15]提出了一種基于極點配置的阻尼環節改進方法，通過調節反饋增益矩陣的參數，改變傳遞函數的極點位置，從而得到期望的系統阻尼比，改善了擾動后的系統暫態響應性能。文獻[16]提出了基于一階滯后環節的暫態電磁功率策略，消除了VSG響應有功參考階躍擾動時輸出有功功率的超調現象，但未考慮電網頻率波動對其輸出功率的影響。

而當雙VSG工作在并聯組網的模式下時[17]，系統的頻率由各個VSG共同決定，各個VSG相互影響，其有功功率振蕩的產生機理更加復雜[18]。文獻[19]建立了考慮控制延時的多VSG并聯系統的狀態空間模型，分析了下垂系數與控制延時對系統穩定性的影響規律。文獻[20]提出了一種暫態阻尼的功率振蕩抑制方法，但是沒有給出具體的參數設計原則。文獻[21]在分析了VSG輸出有功功率與其角加速度之間的關系后，提出了一種附加干擾補償的角加速度控制方法，但所提策略的參數設計不當會造成系統失穩，進而造成更加嚴重的有功功率振蕩。文獻[22]中VSG的轉動慣量為其輸出頻率與其相鄰VSG輸出頻率的差值和輸出頻率的導數項的函數，通過自適應改變轉動慣量的值，保持各個VSG輸出頻率在動態過程中的一致性，有效的減少了有功功率超調和振蕩。文獻[23]為雙VSG系統設計了中央狀態反饋控制器，能夠將系統的極點移動到所需區域以獲得良好的動態響應。文獻[24]提出將阻尼項改為VSG自身輸出頻率與其相鄰VSG輸出頻率的差值函數，又稱為互阻尼項，互阻尼項加速了系統暫態能量的消減，并進行了參數設計與穩定性分析。其本質上與文獻[22]抑制功率振蕩的原理相同，并且都需要用到分布式通信技術。

以上關于研究有功功率振蕩的文獻中，或需要VSG之間進行通訊，從而增加了系統的建設成本，或選擇慣量或阻尼單一的參數自適應變化抑制功率振蕩，沒有充分發揮VSG控制參數靈活可調的特點，考慮到VSG前級儲能容量和系統所需最低慣量的要求，VSG的轉動慣量通常需要在[Jmax，Jmin]范圍內變化，但是以上文獻在構造自適應慣量項與參數設計時未充分考慮這一條件。

在以上文獻研究的基礎上，本文分析了多VSG功率振蕩產生的機理，為了克服現有文獻所提控制策略的不足，提出一種基于功率微分構造自適應慣量與阻尼的功率振蕩抑制策略。其無需通訊，僅需通過測量本地信息，動態期間自適應轉動慣量的變化量始終控制在[Jmax，Jmin]范圍內，確定了關鍵參數的設計準則。通過在MATLAB/Simulink搭建VSG并聯的仿真模型驗證所提控制策略的有效性。

1"虛擬同步發電機原理

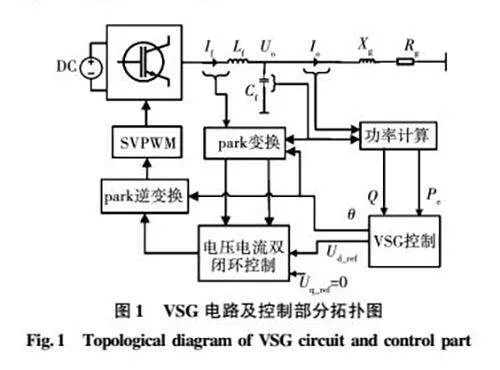
虛擬同步發電機主要包括主電路和控制環節。主電路部分包括三相逆變橋、LC濾波器。圖1是虛擬同步發電機的基本控制框圖，其中：Lf、Cf為輸出濾波電感與濾波電容；Rg為線路電阻；Xg為線路電抗；Uo為濾波電容上的電壓也即VSG的輸出電壓；If為濾波電感上的電流。在逆變器的直流側通常配有儲能裝置以維持直流側電壓的穩定，本文將直流側等效為直流電壓源。

控制部分通常采用三環控制結構，主要包括功率外環，電壓電流內環、調制環節。其中功率外環又分為有功環與無功環。有功環主要模擬同步發電機的轉子運動方程與有功-頻率下垂方程，從而使逆變器具有同步發電機的慣量與阻尼特性，轉子運動方程的表達式為：

式中：Tm代表原動機力矩；Te代表電磁力矩；TD代表阻尼力矩；Pm代表原動機功率，也即VSG的輸入功率；Pe是VSG的輸出電磁功率；D為VSG的阻尼系數；J為其轉動慣量；ω0為VSG的額定頻率；ω為VSG的輸出角頻率;θ為輸出電壓的相位角。VSG的調速器主要模擬同步機的有功頻率下垂特性，其方程可表示為

式中：Pref是VSG的輸出參考功率也即額定有功功率;Kp是VSG的有功頻率下垂系數。有功環產生輸出電壓的電角度。VSG的無功環主要模擬同步發電機的無功-電壓下垂特性，無功-電壓下垂方程為

式中：UN為VSG的額定電壓;Qref為VSG的額定無功功率;Q為VSG的輸出無功功率;Kq為VSG的無功-電壓下垂系數，無功環產生輸出電壓所需的幅值。VSG的功率環控制框圖如圖2。

電壓電流雙閉環控制使VSG的輸出電壓跟蹤功率環計算出的電壓參考值，采用PI控制器以保證較小的誤差與較快的響應速度[25]。

2"雙VSG系統有功功率振蕩分析

本節以雙機并聯系統為例，建立系統的小信號線性化模型，探究并聯系統功率振蕩產生的機理。為了簡化分析和功率解耦，將線路設為以感性為主。雙VSG孤島并聯的電路圖如圖3所示。

圖3中：R1和R2，X1與X2分別是VSG1和VSG2與公共耦合點（point of common couping，PCC）之間的傳輸電阻，傳輸電抗，傳輸電阻為線路電阻和濾波器寄生電阻之和，傳輸電抗為濾波器電抗與線路電抗之和。

E1、δ1、E2、δ2分別為VSG1和VSG2的虛擬內電勢的幅值和功角。Load為系統公共負載。Upcc為PCC點的電壓。

以PCC點為參考點，將VSG的功角設為其輸出電壓與PCC點電壓的相位差，以下i=1，2。VSG的功角表達式為

δi=∫（ωi－ωpcc）dt。（4）

式中ωpcc為公共耦合點的角頻率。圖3中，考慮到線路阻抗以感性為主，即：XgRg，實際中濾波電感也要遠大于其上的寄生電阻，因此總的傳輸電抗也以感性為主，傳輸電阻可忽略。則VSG的輸出功率可表示為

Pei=3EiUpccXisin（δi）。（5）

聯立式（1）和式（2）可得完整的VSG有功環控制方程

Jidωidt=Prefiω0－Peiω0－Kpiω0+Di（ωi－ω0）。（6）

由式（6）可知下垂系數與阻尼系數本質上是同一個參數，阻尼系數也會影響穩態時的功率分配。當VSG工作在孤島模式時，負載將全部由VSG承擔，此時有

從圖4可以看出，負載變化后VSG的輸出有功功率會依次經歷瞬態、動態和穩態過程。

瞬態項是一個不含s項的常數，瞬態過程在負載變化后的瞬間完成。動態過程中VSG1和VSG2輸出的有功功率主要由雙機系統的相對功角差決定，令式（12）中s→0可得穩態時VSGi所承擔的負載功率的情況。

瞬態過程中對應于負載突變后VSG1和VSG2的有功功率增量的比例為

由于分布式電源在地理分布上的分散性，導致每個逆變器到PCC點的傳輸電抗差異較大，每個逆變器的輸出電壓雖然也有差異，但是輸出電壓的比值遠沒有傳輸電抗的比值大，因此瞬態過程中VSG1和VSG2的功率增量的比例也即負載功率在兩個VSG之間的分配情況，主要由傳輸電抗的比例決定。

動態過程的特性取決于傳遞函數（12）的零極點位置。分析式（12）可以發現，當參數滿足式（14）時

G（s）會變成一個不含s項的常數，即傳遞函數的極點會和零點對消，此時傳遞函數G（s）的單位階躍響應呈現階躍特性，動態過程中不會有功率振蕩發生。

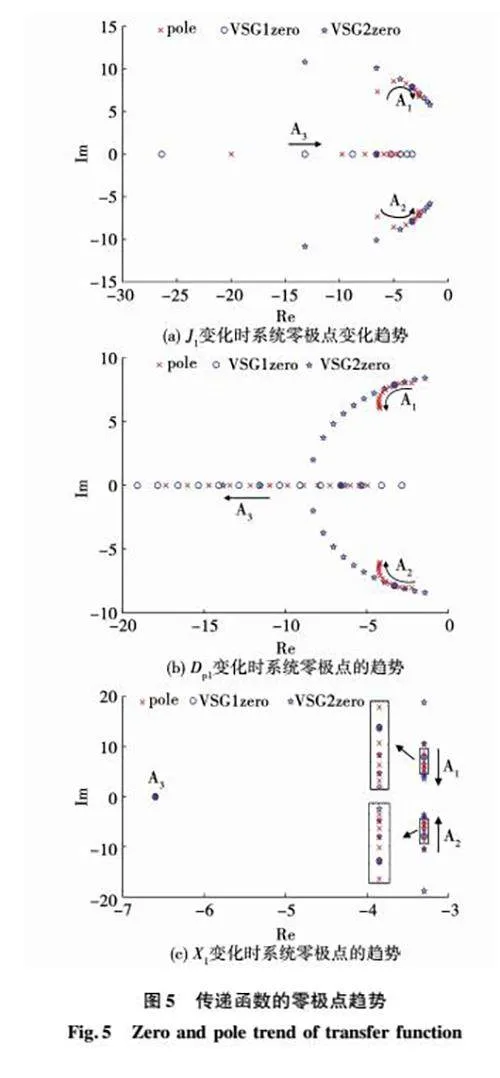
實際工程中VSG1和VSG2的參數并不會嚴格滿足式（14），并且難以根據式（12）寫出反映參數與零極點關系的顯函數。因此，需要研究VSG1和VSG2的J，Dp，X參數分別不滿足式時傳遞函數的零極點變化趨勢。將式（14）中的α設為1。

圖5（a）中Dp1Dp2=X2X1=1；圖5（b）中，J1J2=X2X1=1；圖5（c）中，J1J2=Dp1Dp2=1。

圖5中，如果VSG的各個參數和傳輸電抗符合式（14）時，共軛極點A1，A2會和一對零點相消，此共軛極點不會對系統響應產生影響。如果不符合，共軛極點不會與零點相消，在負載擾動下，此共軛極點對應的輸出有功功率的瞬態響應是一個幅值為指數衰減的正弦振蕩。并且隨著J1的增大，系統極點逐漸向虛軸靠近，振蕩頻率、衰減系數都將減小，系統穩定性降低。隨著等效下垂系數Dp的增加，系統極點遠離虛軸，靠近實軸，振蕩的衰減系數增大，振蕩頻率降低，有功功率的振蕩減小，但是當Dp增加到一定值時，振蕩的衰減系數開始減小，因此通過增大等效下垂系數來減小有功振蕩的作用是有限的。由圖5（c）可知，傳輸電抗只對振蕩頻率有影響，增大傳輸電抗X1會減小振蕩頻率。此外，改變VSG2的參數得到的系統零極點圖與改變VSG1參數得到的系統零極點圖相同，因此這里僅給出VSG1參數改變時系統的零極點圖。

穩態時，系統中每個VSG的輸出角頻率相等，角頻率差為0，輸出有功功率也不會發生變化。根據VSG的有功頻率下垂特性，在負載發生變化后，VSG的輸出角頻率會逐漸從負載變化前的穩態工作點向新的穩態工作點運動，由于轉動慣量J的存在，VSG的輸出角頻率不會突變，但VSG內部的轉矩平衡被打破，使VSG產生一個角加速度ω·，如式（16）[26]所示。

ω·=Tm-Te-TDJ。（16）

在VSG的輸出角頻率向新的穩態工作點運動的動態過程中，如果系統中VSG的角加速度不同，則其輸出頻率也不會相同，相應的VSG之間的角頻率差不等于0，相應的會引起VSG之間輸出有功功率的振蕩，并且角頻率差越大振蕩越劇烈，輸出頻率較大的VSG會承擔更多的系統負載。根據式（16），輸出電磁功率的增加也會減小VSG的角加速度，從而阻止角頻率差的增大，通常負載擾動后的第一個振蕩周期角頻率差的絕對幅值最大，在系統穩定的前提下，此后每一個振蕩周期角頻率差的幅值會逐漸減小，有功功率的振蕩也會減小。根據前文繪制的零極點圖5可知，當雙機系統的參數滿足式（14）時，傳遞函數極點與零點對消，此時對于VSG的輸出頻率，在動態過程中每個VSG的角加速度相等，輸出頻率始終保持一致，角頻率差始終為0，因此動態過程中不會產生有功功率振蕩。

3"基于改進虛擬阻抗與自適應慣量與阻尼的控制策略

3.1"基于改進虛擬阻抗的瞬態功率均分策略

由第二節的分析可知，瞬態過程中VSG1和VSG2的有功功率增量的比例取決于傳輸電抗的比例，理想情況下總是希望VSG1和VSG2的傳輸電抗的比例等于其額定容量的比例以達到功率均分的目的。但是，在實際工程中當并聯VSG傳輸電抗的比例不等于額定容量的比例時，將導致一部分VSG承擔過多的系統負載，不能實現負載按其額定容量分配。為了解決這一問題，可以通過運用虛擬阻抗等效的改變傳輸阻抗，使并聯VSG傳輸阻抗的比例與其額定容量的比例一致。

但是所加的虛擬阻抗過大又會使穩態時VSG的輸出電壓偏移嚴重，降低電能質量。因此，本文在傳統虛擬阻抗的基礎上提出改進的虛擬阻抗策略。

將輸出電流乘以虛擬阻抗可以模擬實際線路中有電流經過時產生的電壓降效果，虛擬阻抗值越大，電壓降越大。基于dq軸的傳統虛擬阻抗表達式為：

式中：iodq輸出電流的dq軸分量;Rv、Lv為虛擬電阻和虛擬電感;ΔUdq為虛擬阻抗上的電壓降。本文提出的改進虛擬阻抗的表達式為：

其中T為一階低通濾波器的時間常數。由式（18）可知，在負載突變的瞬態，一階低通濾波器的輸出不能立即跟隨iodq，作用在虛擬阻抗上的電流為輸出電流的增量部分，在虛擬阻抗上產生電壓降，從而等效的改變傳輸阻抗。而隨著VSG的輸出電流到達穩態，一階低通濾波器的輸出等于iodq，作用在虛擬阻抗上的電流為零，在虛擬阻抗上也不會產生電壓降。因此，改進的虛擬阻抗策略可以在不帶來穩態電壓降的情況下改善并聯VSG的瞬態功率分配特性。

3.2"基于功率微分項的振蕩抑制策略

如前所述，當雙機系統的參數和傳輸電抗不符合式（14）時，在動態過程中會出現功率振蕩，將參數全部按照條件（14）進行設置可以消除有功振蕩，但是這會降低參數選擇的自由度，并且轉動慣量受到前級儲能容量的限制。保持動態過程中并聯VSG輸出頻率的一致性可以減小有功功率振蕩，由式（16）可知，通過自適應改變慣量與阻尼可以改變VSG的角加速度，從而間接的改變VSG的輸出頻率，這為保持VSG輸出頻率的一致性提供了可能。

雙機系統中負載擾動后典型VSG角頻率波形如圖6所示。每個時間段內的角頻率差ωi－ωm以及角頻率變化率dωi/dt變化特性不同，為了保持動態過程中每個VSG輸出角頻率的一致性，每個時間段對慣量與阻尼的要求也不同。在給出慣量與阻尼的變化規律之前需要首先推導用于構造自適應慣量與阻尼的有功功率微分項的表達式。

3.2.1"功率微分項函數

對于孤島運行模式下的雙VSG并聯系統，其網絡模型可由節點導納矩陣表示，每個VSG的輸出功率為

式中zgt;0。式（22）表明P·e可以反映并聯VSG之間的輸出角頻率差異，但是注意到穩態后負載變化的瞬間會導致VSG輸出電壓與PCC點的電壓相位差發生突變，此時P·e表征的是相位差的突變，并不反映VSG之間的角頻率差異。通常在相位差突變時，P·e在兩個計算周期的值相差較大，持續時間短。功率振蕩時的P·e是VSG角頻率差的函數，其值在兩個計算周期的差很小，持續時間長。因此，可以對P·e在兩個計算周期值的差的大小進行判斷來區分兩者。此外，為了防止引入高頻干擾，首先需要對有功功率Pe進行低通濾波后得到Pef，并將其用于區分算法中：

式中：L為兩個計算周期P·ef的差的最大值；P·ef_last為上一計算周期的P·ef值。經過區分算法后得到的P·efs可以準確的反映出VSG之間的角頻率差異。

3.2.2"功率微分自適應慣量控制

由式（16）可知，轉動慣量J與VSG的角加速度成反比。定義雙機系統的角頻率差Δω=ω1－ω2。圖6中，t1時系統發生負載擾動，以VSG1為例，在t1～t2和t3～t4時間段內，其Δωω·1gt;0，此時應該增大其轉動慣量J1以減小其動態響應速度，阻止ω1偏離ω2。在t2～t3和t4～t6時間段內，其Δωω·1lt;0，此時應減小轉動慣量J1以加快其動態響應速度，使ω1加速趨向于ω2。VSG2轉動慣量J2的變化規律與VSG1相似。通過在各個階段改變轉動慣量J的大小，可以使VSG1和VSG2時刻趨于相同的輸出角頻率。

對于雙VSG系統，其角頻率差及其角頻率變化率的情況與對應的轉動慣量調節原則如表2所示。

表2中的角頻率變化率可以通過本地測量獲得，由3.2.1節的分析可知角頻率差可由本地有功功率微分項間接獲得。因此，本文提出的自適應轉動慣量方程為

式中：J0為穩態時的初始轉動慣量；Jmax、Jmin為轉動慣量的最大值和最小值；a為轉動慣量補償系數；sgn為符號函數。

3.2.3"有功功率微分阻尼控制

傳統VSG的阻尼項對有功功率振蕩的抑制作用不大，并且由于下垂系數與阻尼系數相互耦合，導致阻尼系數會影響穩態時的有功功率均分。

本文提出的基于功率微分項的改進阻尼控制如下：

TD=DP·efs。（25）

式中D為阻尼系數。

在系統負載擾動下，每個VSG的輸出角頻率會發生變化。將式（22）代入式（25），則改進的阻尼項可等效為

TD=Dz（ωi－ωk）。（26）

在雙機系統中，系統負載擾動發生后，如果ω1gt;ω2，在VSG1的有功環中，改進阻尼項表現為制動性質的力矩；在VSG2的有功環中，改進阻尼項表現為加速力矩。通過改進阻尼項在VSG1和VSG2的有功環路中附加的制動和加速力矩，可以使VSG1和VSG2的角頻率差更快的減小至零，從而有助于保持動態過程中VSG輸出角頻率的一致性。當ω1lt;ω2時，也可以得到類似的結論。因此，改進的阻尼項可以減小動態過程中的角頻率差，從而抑制有功功率振蕩，提高系統的頻率穩定性。

并且由于穩態時P·efs=0，此時改進阻尼項不會對有功環路造成影響，系統的功率分配只由有功頻率下垂環節決定，因此與傳遞的阻尼項相比，改進阻尼項不會影響穩態時的系統功率分配。

4"仿真驗證

4.1"改進虛擬阻抗策略驗證

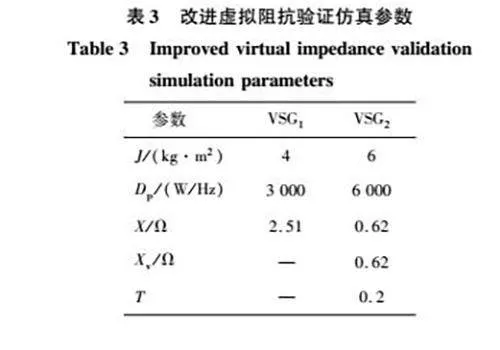
本節通過MATLAB/Simulink搭建含有公共母線的雙VSG并聯仿真模型，以驗證所提改進虛擬阻抗策略的有效性，系統中各參數見表3。

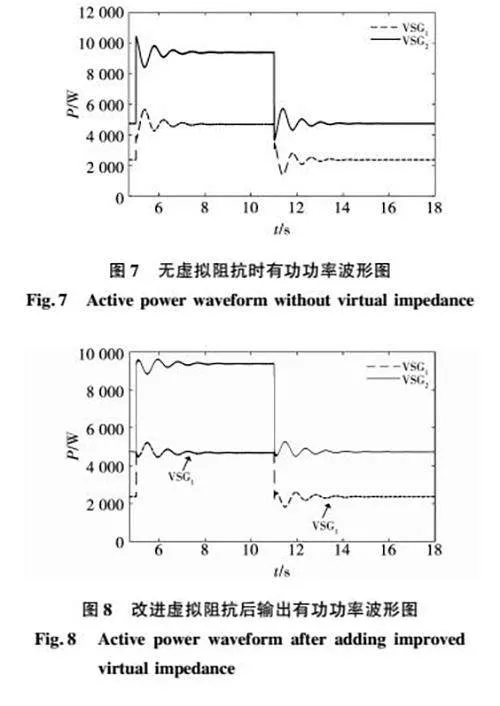
仿真工況為：在0 s時，仿真啟動，此時系統的初始負荷為7 000 W，穩定后VSG1和VSG2輸出功率分別為2 340、4 660 W，VSG1和VSG2的額定容量比為1∶2，按照額定容量分擔系統的負荷，在5 s時系統負荷增加了7 000 W，在11 s時系統負荷減小7 000 W。

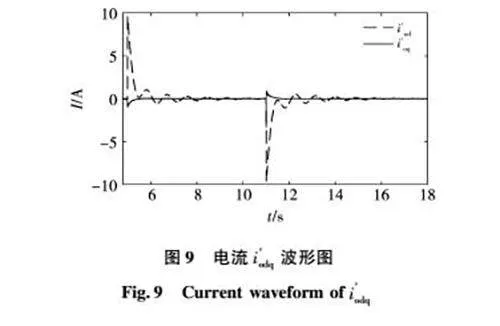
圖7和圖8分別為無虛擬電抗和改進虛擬電抗后的輸出有功功率波形圖。以5 s時系統負荷突增為例，在無虛擬阻抗時，VSG1和VSG2的輸出有功功率增量的比為5 600∶1 400，與傳輸電抗的比1/2.51∶1/0.62相等，與前文的理論分析結果一致。但是由于傳輸電抗的比例并不等于額定有功功率的比例，導致在負荷改變的瞬態不能實現功率均分。當為VSG2增加改進0.6Ω的虛擬電抗后，VSG1和VSG2傳輸電抗的倒數比為1/2.51∶1/1.24，輸出有功功率的增量的比為4 600∶2 400，約等于額定容量的比例，實現了瞬態過程中負荷按照額定容量均分。令i′odq=（1－1/（Ts+1））iodq，i′odq為作用在虛擬阻抗上的電流，由圖9可知，在瞬態和動態過程中，其值不為零，但是在穩態時由于低通濾波器的輸出與i′odq相等，因此，穩態時其值等于零，虛擬阻抗上的壓降也為零，即穩態時改進的虛擬阻抗不會導致VSG的輸出電壓跌落。

4.2"基于有功功率微分項的慣量與阻尼策略驗證

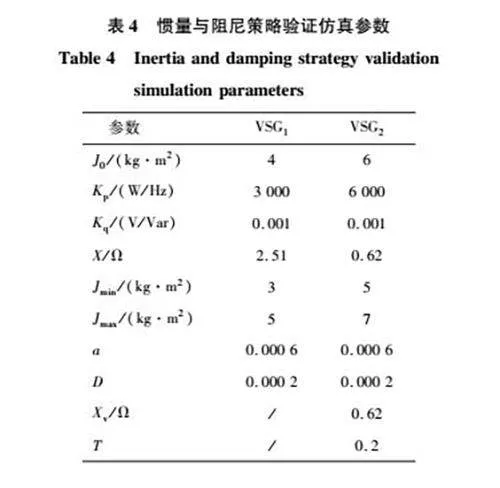
改進虛擬阻抗主要解決由于傳輸電抗不匹配導致瞬態時的功率不能均分問題。基于有功功率微分項的自適應慣量與阻尼策略主要解決的是動態過程中的功率振蕩問題，本節主要驗證所提自適應慣量與阻尼策略的有效性，所使用的仿真參數如表4所示，仿真工況與上節相同。

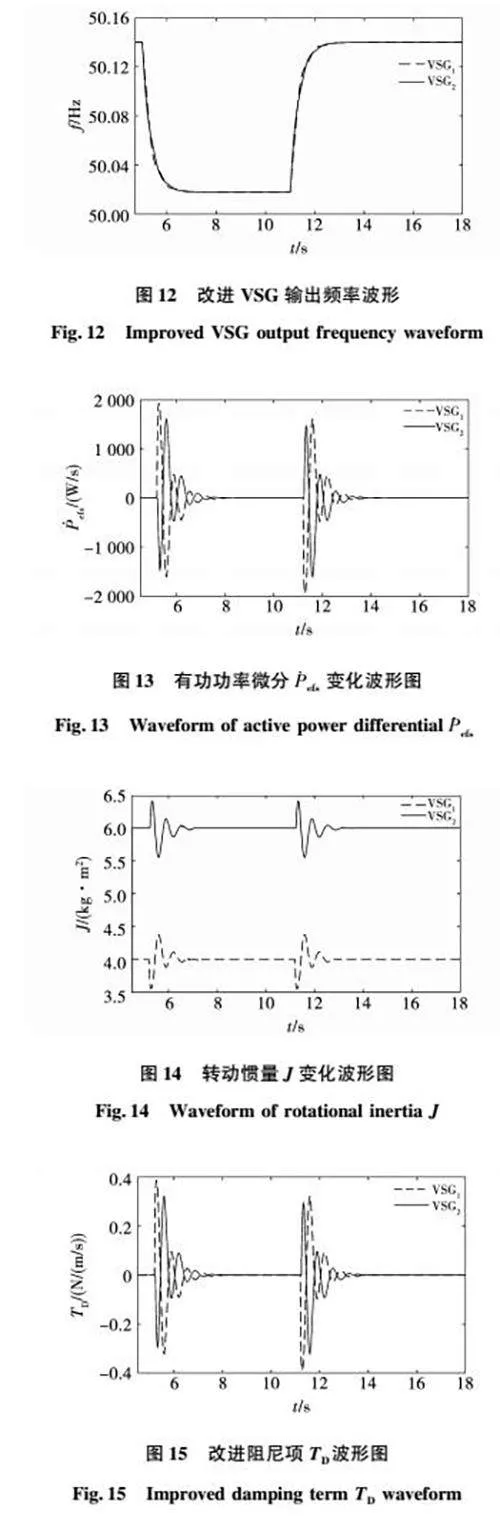
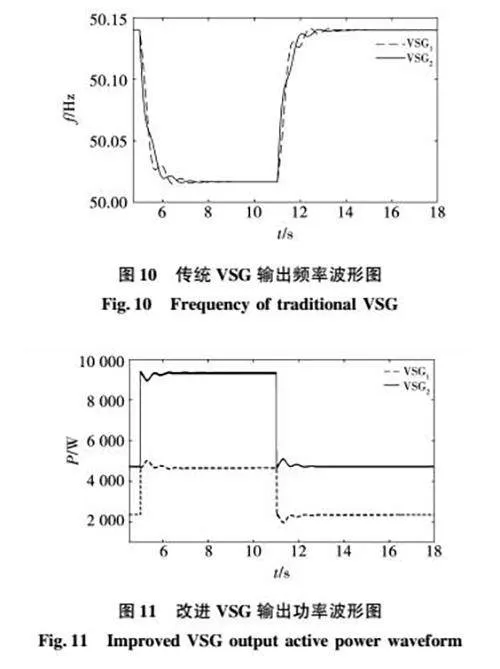
圖10為傳統VSG的輸出頻率波形圖。圖11和圖12分別為采用了改進虛擬阻抗與自適應慣量和阻尼策略的改進VSG的輸出功率與頻率波形圖。圖13為有功功率微分項P·efs的變化波形圖。圖14和圖15分別是轉動慣量J和阻尼項Td的變化波形。由式（25）可知，改進阻尼項TD和P·efs僅差一個常數D，則圖15和圖13的波形圖趨勢相同。對比傳統VSG的輸出功率與頻率可知，在本文提出的改進控制策略下，動態過程中有功功率振蕩明顯被抑制，頻率的動態特性明顯提升，VSG之間輸出頻率的差異較小。以5 s時負載突增為例，傳統VSG1的超調量為20.7%，振蕩過程約為2.2 s，而改進VSG方案的超調量僅有8.5%，振蕩過程僅持續約1.2 s，超調量減小了41%，到達穩態的時間減小了1 s。對比圖7和圖8可以發現改進虛擬阻抗策略也減小了動態時的有功功率振蕩，但對比圖8和圖11，可以發現動態時的有功振蕩幅值和振蕩時間明顯減小，從而證明了基于有功功率微分項的自適應慣量與阻尼策略對動態時的有功振蕩抑制作用的有效性。由圖14和圖15可知，轉動慣量和阻尼項的變化有利于VSG1和VSG2的輸出頻率趨于一致，以轉動慣量為例，穩態時J02∶J01=3∶2，比值約為1.5，在負載突增瞬間，各個參數的比例越接近額定容量的比例，其角加速度就越趨近于一致，頻率一致性越好，由圖14可知，在負載突增后轉動慣量的比J2∶J1=6.3∶3.6，比值為1.75，更接近額定容量的比值2。文獻[22，24]提出的改進方案需要運用分布式通信技術使VSG交換各自的輸出角頻率信息，極大的增加了系統的建設成本。本文發現VSG輸出有功功率微分項是角頻率差的函數，因此可用輸出有功功率微分項的值作為角頻率差的值，而VSG的輸出有功功率在有功控制環中已經采集過，因此無需增加額外的測量和通訊裝置。

5"結"論

1）建立了雙VSG并聯系統的線性化小信號模型，獲得了在負載擾動下每個VSG輸出有功功率的傳遞函數以及雙機系統的等效小信號模型。將VSG的輸出有功功率過程依次分為瞬態、動態和穩態3個階段。研究結果表明，在負載變化的瞬態階段，VSG輸出有功功率的增量的比例取決于各自傳輸阻抗倒數的比例，動態過程由傳遞函數零極點位置決定，當各個VSG控制參數和線路電抗的比例相等時，傳遞函數的極點與零點相消；不相等時，極點不會與零點相消，并且極點中包含一對共軛極點，該共軛極點對應得響應會引起動態階段VSG的有功功率振蕩。參數比例不匹配也會導致動態過程中各個VSG的輸出角頻率不相等，從而引起有功功率的振蕩。

2）采用改進的虛擬阻抗策略可以使VSG等效傳輸阻抗倒數的比例等于其額定容量比。推導了雙機孤島并聯模式下VSG輸出有功功率，發現其微分項是角頻率差的函數。根據兩機系統振蕩時的典型頻率圖，以及抑制振蕩相應的轉動慣量J和阻尼項Td變化規律，提出了自適應慣量和阻尼的有功功率振蕩抑制方法。仿真結果表明，相比傳統VSG的控制方案，改進虛擬阻抗策略可以使瞬態時并聯VSG實現按照額定容量均分負載，自適應慣量與阻尼策略可以使動態時有功功率振蕩幅值從5 600 W減小到5 100 W，超調量減小了41%，到達穩態的時間減小了1 s。

參 考 文 獻：

［1］"王成山，武震，李鵬，等. 微電網關鍵技術研究[J].電工技術報，2014，29（2）：1.

WANG Chengshan，WU Zhen，LI Peng，et al. Research on key technologies of microgrid[J]. Transactions of China Electrotechnical Society，2014，29（2）：1.

［2］"王成山，李鵬. 分布式發電、微網與智能配電網的發展與挑戰[J].電力系統自動化，2010，34（2）：10.

WANG Chengshan，LI Peng. Development and challenges of distributed generation，the microgrid and smart distribution system[J]. Automation of Electric Power Systems，2010，34（2）：10.

［3］"楊新法，蘇劍，呂志鵬，等. 微電網技術綜述[J].中國電機工程學報，2014，34（1）：57.

YANG Xinfang，SU Jian，L Zhipeng，et al. Overview on microgrid technology[J]. Proceedings of the CSEE，2014，34（1）：57.

［4］"顏寧，潘霄，張明理，等. 基于多時間尺度的微電網群階梯控制方法研究[J].電機與控制學報，2019，23（9）：26.

YAN Ning，PAN Xiao，ZHANG Mingli，et al. Step control method of multimicrogrids based on different time levels[J].Electric Machines and Control，2019，23（9）：26.

［5］"王博，楊德友，蔡國偉，等. 高比例新能源接入下電力系統慣量相關問題研究綜述[J]. 電網技術，2020，44（8）：2998.

WANG Bo，YANG Deyou，CAI Guowei，et al. Review of research on power system inertia related issues in the context of high penetration of renewable power generation[J]. Power System Technology，2020，44（8）：2998.

［6］"ZHONG Q C，WEISS G. Synchronverters： inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics，2011，58（4）：1259.

［7］"張玉治，張輝，賀大為，等. 具有同步發電機特性的微電網逆變器控制[J]. 電工技術學報，2014，29（7）：261.

ZHANG Yuzhi，ZHANG Hui，HE Dawei，et al. Control strategy of micro grid converters with synchronous generator characteristic[J]. Transactions of China Electrotechnical Society，2014，29（7）：261.

［8］"丁明，楊向真，蘇建徽，等. 基于虛擬同步發電機思想的微電網逆變電源控制策略[J]. 電力系統自動化，2009，33（8）：89.

DING Ming，YANG Xiangzhen，SU Jianhui，et al. Control strategies of inverters based on virtual synchronous generator in a microgrid[J]. Automation of Electric Power Systems，2009，33（8）：89.

［9］"CHEEMA K M. A comprehensive review of virtual synchronous generator[J]. International Journal of Electrical Power amp; Energy Systems， 2020， 120：106006.

［10］"WU H， RUAN X， YANG D， et al. Smallsignal modeling and parameters design for virtual synchronous generators[J]. IEEE Transactions on Industrial Electronics，2016，63（7）：4292.

［11］"ZHANG B， ZHANG J. Smallsignal modeling and analysis of a threephase virtual synchronous generator under offgrid condition[J]. Energy Reports，2022，8：1200.

［12］"王亞維，劉邦銀，段善旭，等. 虛擬同步控制的暫態特性優化策略研究[J]. 中國電機工程學報，2019，39（20）：5885.

WANG Yawei， LIU Bangyin， DUAN Shanxun， et al. Research on transient characteristic optimization of virtual synchronization generator control strategy[J].Proceedings of the CSEE，2019，39（20）：5885.

［13］"李明烜，王躍，徐寧一，等. 基于帶通阻尼功率反饋的虛擬同步發電機控制策略[J]. 電工技術學報，2018，33（10）：2176.

LI Mingxuan，WANG Yue，XU Ningyi， et al. Virtual synchronous generator control strategy based on bandpass damping power feedback[J]. Transactions of China Electrotechnical Society，2018，33（10）：2176.

［14］"徐海珍，張興，劉芳，等. 基于超前滯后環節虛擬慣性的VSG控制策略[J].中國電機工程學報，2017，37（7）：1918.

XU Haizhen，ZHANG Xing，LIU Fang，et al. Virtual synchronous generator control strategy based on leadlag link virtual inertia[J]. Proceedings of the CSEE，2017，37（7）：1918.

［15］"LIU J， MIURA Y， ISE T. A novel oscillation damping method of virtual synchronous generator control without PLL using pole placement[C]//2018 International Power Electronics Conference （IPECNiigata 2018ECCE Asia）， May 20-24， 2018， Niigata， Japan. 2018： 775-781.

［16］"蘭征，龍陽，曾進輝，等. 引入暫態電磁功率補償的VSG控制策略[J]. 電網技術，2022，46（ 4）：1421.

LAN Zheng，LONG Yang，ZENG Jinhui，et al. VSG control strategy introducing transient electromagnetic power compensation[J]. Power System Technology，2022，46（4）：1421.

［17］"萬曉鳳，詹子錄，丁小華，等.基于虛擬同步發電機的多逆變器并聯改進控制策略[J].電機與控制學報，2020，24（2）：118.

WANG Xiaofeng，ZHAN Zilu，DING Xiaohua，et al. Improved control strategy of multiinverter parallel based on virtual synchronous generator[J]. Electric Machines and Control，2020，24（2）：118.

［18］"杜威，姜齊榮，陳蛟瑞，等. 微電網電源的虛擬慣性頻率控制策略[J].電力系統自動化，2011，35（23）：26.

DU Wei，JIANG Qirong，CHEN Jiaorui，et al. Frequency control strategy of distributed generations based on virtual inertia in a microgrid[J].Automation of Electric Power Systems，2011，35（23）：26.

［19］"涂春鳴，謝偉杰，肖凡，等. 多虛擬同步發電機并聯系統控制參數對穩定性的影響分析[J].電力系統自動化，2020，44（15）：77.

TU Chunming，XIE Weijie，XIAO Fan，et al. Influence analysis of control parameters of parallel system with multiple virtual synchronous generators on stability[J]. Automation of Electric Power Systems，2020，44（15）：77.

［20］"SHUAI Z， HUANG W， SHEN Z J， et al. Active power oscillation and suppression techniques between two parallel synchronverters during load fluctuations[J]. IEEE Transactions on Power Electronics，2020，35（4）：4127.

［21］"CHEN M， ZHOU D， BLAAJERG F. Active power oscillation damping based on acceleration control in parallel virtual synchronous generators system[J]. IEEE Transactions on Power Electronics，2021，36（8）：9501.

［22］"FU S，SUN Y， LIU Z， et al. Power oscillation suppression in multiVSG grid with adaptive virtual inertia[J].International Journal of Electrical Power amp; Energy Systems，2022，135：107472.

［23］"POURMOHAMMAD M， TOULABI M. Designing a central MIMO state feedback controller for a microgrid with multiparallel VSGs to damp active power oscillations[J]. International Journal of Electrical Power amp; Energy Systems，2021， 133（5）：106984.

［24］"洪灝灝，顧偉，黃強，等.微電網中多虛擬同步機并聯運行有功振蕩阻尼控制[J].中國電機工程學報，2019，39（21）：6247.

HONG Haohao， GU Wei， HUANG Qiang， et al. Power oscillation damping control for microgrid with multiple VSG units[J]. Proceedings of the CSEE，2019，39（21）：6247.

［25］"余裕璞，顧煜炯，和學豪，等. 逆變器電壓電流雙閉環控制系統設計[J].電力科學與工程，2019，35（3）：1.

XU Yupu， GU Yujiong， HE Xuehao， et al. Design of voltage and current double closedloop control system for inverter[J]. Electric Power Science and Engineering，2019，35（3）：1.

［26］"郭建祎，樊友平.基于改進粒子群算法的VSG參數自適應控制策略[J].電機與控制學報，2022，26（6）：72.

GUO Jianwei， FAN Youping. Adaptive VSG parameter control strategy based on improved particle swarm optimization[J].Electric Machines and Control，2022，26（6）：72.

（編輯：劉素菊）

收稿日期： 2022-08-11

基金項目：國家自然科學基金（U1504506）；河南省科技攻關項目（202102210093，212102210256）；河南省高等學校青年骨干教師培養計劃項目（2020GGJS055）；河南理工大學青年骨干教師培養計劃項目（2018XQG-08）

作者簡介：朱"軍（1984—），男，博士，副教授，研究方向為新能源發電、特種電機驅動與控制；

袁亞飛（1997—），男，碩士研究生，研究方向為虛擬同步發電機；

劉鵬輝（1992—），男，博士，講師，研究方向為電力系統繼電保護；

杜少通（1985—），男，博士，副教授，研究方向為多電平變流器控制、電能質量控制；

郭向偉（1987—），男，博士，副教授，研究方向為電力電子技術、新能源汽車能量管理系統；

楊"明（1982—），男，博士，副教授，研究方向為新能源并網發電技術、虛擬同步發電機等；

曲玉博（1996—），男，碩士研究生，研究方向為虛擬同步發電機技術。

通信作者：朱"軍