提出好的問題是問題教學的核心

馬林剛

數學是問題的學科，提出問題、解決問題在解題的過程中往往起著關鍵作用，通過提出問題、解決問題，架設起已知和未知之間的橋梁.同樣一個問題，從不同的角度進行分析、聯想，建立不同的解題思路，會提出不同的問題，但落腳點都是解決問題.在教學中鼓勵學生展示思考的成果，教師和學生一起提出問題、解決問題.不僅提高了學生的思維水平、表達能力，還豐富了學生解題體驗，拓寬了解決問題的內涵，提升對數學問題的認知.本文以教學中處理一道習題的過程為例，談提出好的問題在解決問題中的作用.

問題 （2022年全國高中數學聯賽四川預賽試題第5題）已知函數f：{1，2，…，10}→{1，2，3，4，5}，且對一切k=1，2，…，9，有|f（k+1）－f（k）|≥3.則符合條件的函數f的個數為 .

分析：老師布置此題目作為課后思考題，給了學生充足的時間思考.講解之初，由老師拋磚引玉.

一道看似很簡單考察函數的定義的題目，似乎用列舉就可以輕而易舉的解決.但實際操作起來卻發現很復雜，容易算錯.

講解之前教師提出三個問題：

（1）怎樣化繁為簡，研究出問題的本質，得到準確的答案？

（2）哪些數學解題思想在主導著解決問題的方向？

（3）此問題還可以怎樣變形？

首先，直接列舉：

雖然發現到了一些對解題有作用的性質：（1）f（x）≠3.若f（x）=3，f（x-1）或f（x+1）沒有解.（集合{1，2，3，4，5}中最大的元素為5，最小的元素為1，|3－1|=|5－3|=2<3）f（x）的可能取值只能是集合{1，2，4，5}中的4個元素；（2）函數值隨著自變量的改變呈現類似于周期性的性質；（3）考慮對題目做“退化”處理，研究f：{1，2，…，5}→{1，2，3，4，5}，或者研究f：{1，2，…，4}→{1，2，3，4，5}.

其次，教師再次提出問題：退化處理后發現解決確定函數的過程就是確定定義域內每個元素的象.但是題目要求并不是求出這些函數，而是求出符合條件的函數的個數，是否可以把這個周期性用得更寬泛？

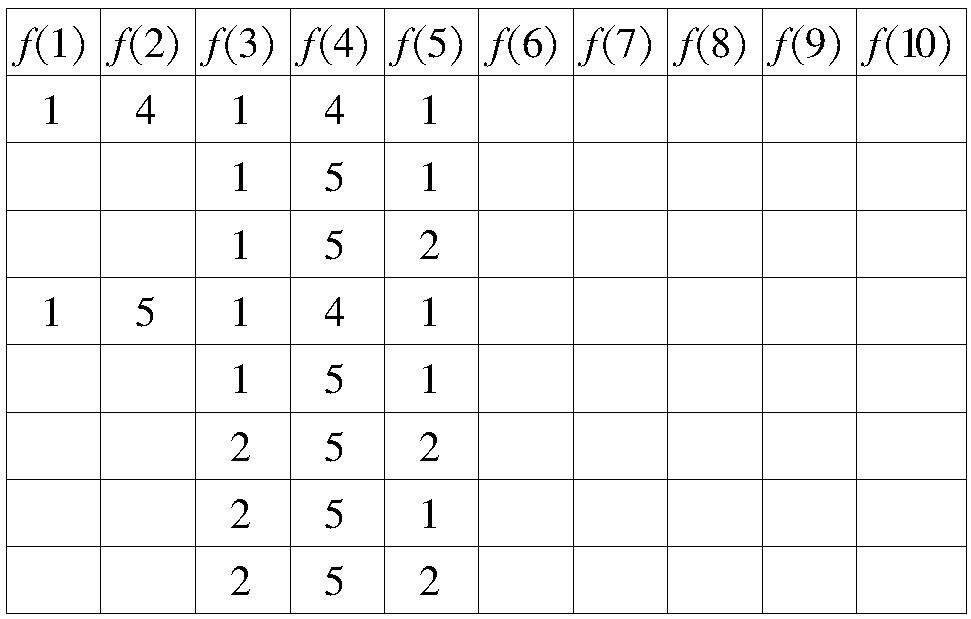
這時想到的是從f（1）→f（5），f（5）→f（10）結果不夠理想.于是列出表格：

繼續進行討論：當f（1）=1時，f（4）有2種時候等于4，有3種時候等于5；

當f（1）=2時，f（4）有1種時候等于4，有2種時候等于5；當f（1）=4時，f（4）有2種時候等于1，有1種時候等于2；當f（1）=5時，f（4）有3種時候等于1，有2種時候等于2.

繼而得到： f（4）會出現5次1，3次2，3次4，5次5.對于f（7）而言，f（4）=1會產生5×2次4，5×3次5；f（4）=2會產生3×1次4，3×2次5；f（4）=4會產生3×2次1，3×1次2；f（4）=5會產生5×3次1，5×2次2.共有21次f（7）=1，13次f（7）=2，13次f（7）=4，21次f（7）=5.對于從f（7）到f（10），f（7）=1得到f（10）有21×5種情況，f（7）=2得到f（10）有13×2種情況，f（7）=4得到f（10）有13×3種情況，f（7）=5得到f（10）有21×5種情況.共計288種情況.

教師：這是本人的做法，解答比較繁雜，自己覺得成功之處在于分三步走，先退化到簡單情形，本來想兩步解決，但列舉時發現可以分三次走更輕松.個人覺得沒有把題目蘊含的本質搞清楚，只看到了問題的一面.對題目的本質局限在函數的定義，沒有找到更好的數學模型.

教師提出問題：本題還可以做什么樣的推廣和拓展？

學生甲：我先證明一個引理：從左至右m個位置（m≥2n+1），n個相同的元素放在m個位置，要求這n個元素互不相鄰，有Cnm－n+1種放法.

因為n個元素要占用n個位置且不相鄰，所以需要用m－n個座位來隔開這n個元素，于是出現m－n+1個空格（因為兩端各有1個，中間有m－n－1個），n個元素在這m－n+1個空格種選擇，因為不分彼此，所以有Cnm－n+1種放法.

這對于本題有什么作用呢？我們先來看一種特殊情形：5 1 5 1 5 1 5 1 5 1 .

現在5的位置可以用4替換，1的位置可以用2替換，但是相鄰的兩個數不能同時被替換，那樣就不滿足|f（k+1）－f（k）|≥3.而 1 5 1 5 1 5 1 5 1 5 的情況與之類似，故總的對應有2（C010－0+1+C110－1+1+C210－2+1+C310－3+1+C410－4+1+C510－5+1）=2（C011+C110+C29+C38+C47+C56）個.

教師：甲同學的解答重在建立了一種可靠的模型，比我的做法簡單很多，值得借鑒，把不熟悉的問題通過建立模型轉化到熟悉的場景下解決是常用的方法.給甲同學掌聲鼓勵.

教師再次提出問題：（1）可以用有限歸納的方法來討論嗎？（2）如果用有限歸納的方法討論是不是不嚴謹？（3）怎么處理這個不嚴謹的問題？

我發現乙同學的做法很有趣，他回答了問題（1），下面請乙同學在黑板上板書講解.

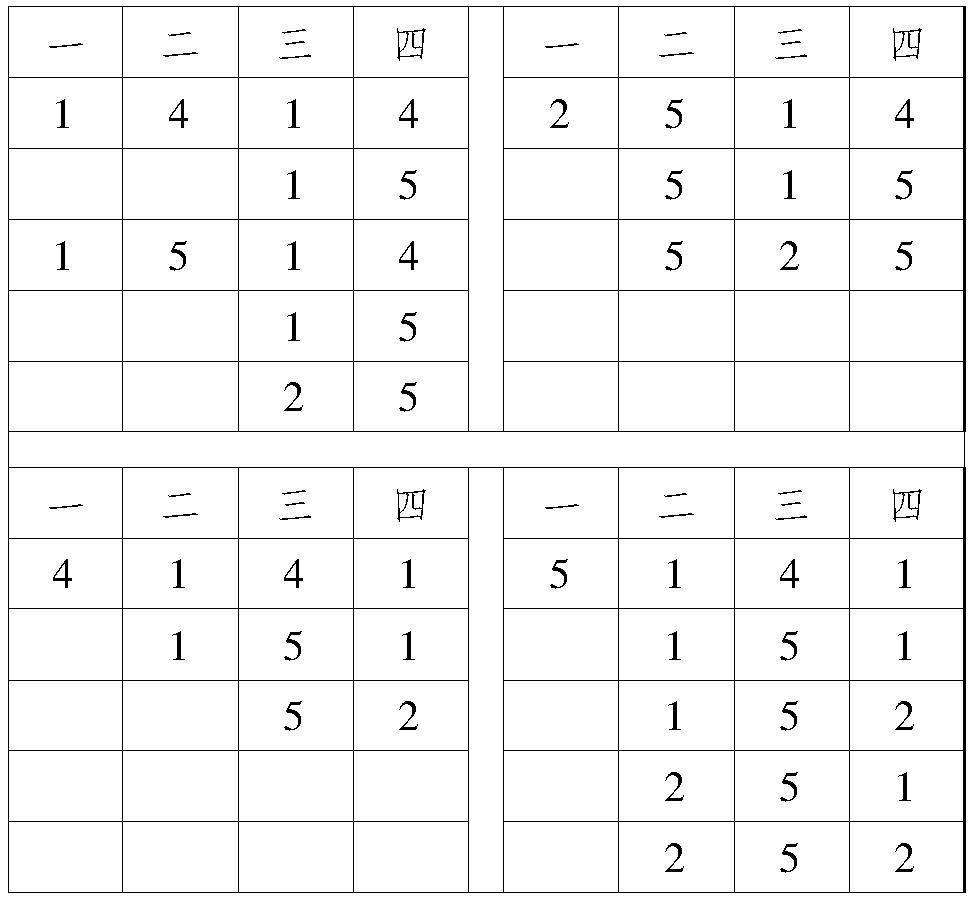
乙同學：我也是列舉了一個樹狀圖，不過是以對應的種數來列的，結果好象出現了斐波那契數列.首先：確立如右的對應，建立這樣的對應是基于1和5有相同的屬性，就是對應的元素可以有兩種情形，如f（k）=1，則f（k+1）=4或者5；f（k）=5，則f（k+1）=1或者2；而如果f（k）=2，則f（k+1）=5；f（k）=4，則f（k+1）=1.于是A→B或A，而B→A.

經過有限歸納，我猜想：接下來是

當f（1）=1或者2時，情況一樣，也是144種，所以共有288個對應.如下所示.

教師：乙同學做得很棒，如果能夠給后面的推導有個更加嚴格的說明就好了.有沒有同學想好的？

丙同學：還是針對黑板上的情況，我們分析f（k）=ak，{an}滿足斐波那契數列，就是要滿足：①a1=a2=1，②n≥2時，an+1=an+an－1.顯然①滿足，對于②，f（k－1）出現了x個A，y個B，即an-1=x+y.則f（k）出現了x+y個A，x個B，即an=（x+y）+x；于是f（k+1）出現了x+（x+y）個A，x+y個B，即an+1=x+（x+y）+（x+y）=3x+2y=an－1+an.

教師：謝謝丙同學給出了相對嚴格的證明.乙同學借助斐波那契數列的模型解決了問題，丙同學的分析也很科學.本題的求解中對于條件的簡化與假設都是值得學習的，這就是去偽存真，抓住本質的過程.希望同學多思考，多總結，多交流，把學習數學、深化問題解決越做越好.感謝三位同學的精彩分析.

課后記：縱觀三種做法，乙同學的做法在得到丙同學的嚴格證明后不失為最接近本質的做法，甲同學借助的排列組合知識值得肯定，只有老師的做法顯得不夠精巧，說明同學們的思維非常開放而又靈活，值得表揚.合理聯想，建立契合題目的數學模型，是今后解決問題中應該有意考慮的問題.