教材中的兩道例習題解法對比及問題探究

侯懷有 王志華

習題是教材的重要組成部分，是課堂教學內容的鞏固和深化，也應當為學生發展數學核心素養提供平臺［1］.大量的習題是在典型例題的基礎上通過各種變式演變而成的，屬于數學通性通法的解題策略也不多，大部分屬于一題一用的解題技巧.因此，如果能夠優化教科書習題的設計，聚焦核心的數學概念和通性通法，不僅有助于學生對核心數學內容的理解，積累重要的數學活動經驗和理解重要的數學思想方法，而且可以減輕學生的負擔.本文對兩道例習題的解法進行對比，引出對φ的范圍以及求解φ值的方法兩個問題進行探究，尋找求解φ值的通性通法.

一、問題提出

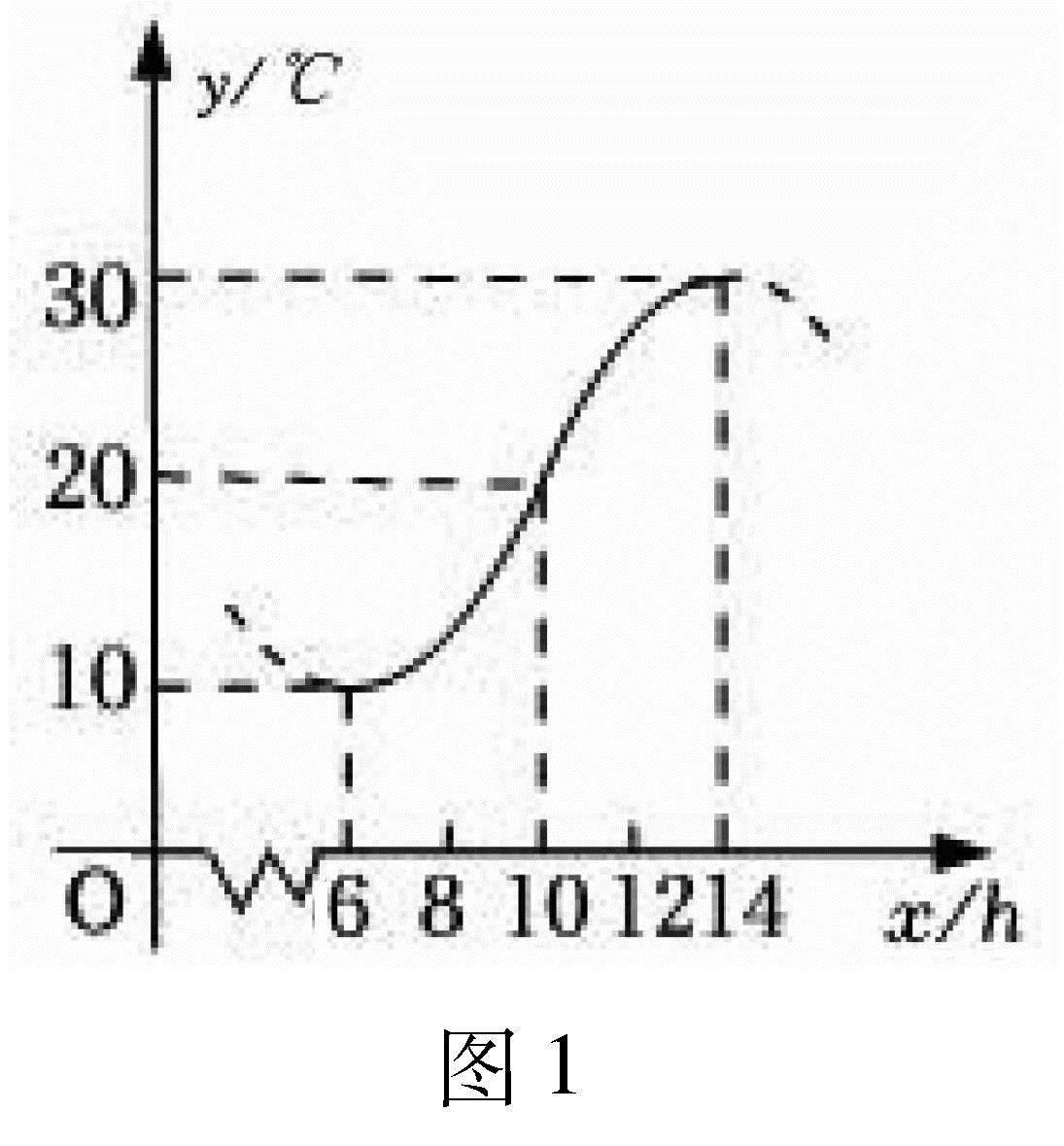
普通高中教科書數學必修第三冊（人教A版）第245頁例1：如圖1，某地一天從6～14時的溫度變化曲線近似滿足函數y=Asin（ωx+φ）+b.

（1）求這一天6～14時的最大溫差；

（2）寫出這段曲線的函數解析式．

教科書給出的解答：（1）由圖1可知，這段時間的最大溫差是20℃.

普通高中教科書數學必修第三冊（人教B版）第68頁第8題：如圖2，某地一天從6時到14時的溫度變化曲線近似滿足函數y=Asin（ωx+φ）+b，其中A＞0，且函數在6時與14時分別取得最小值（最低溫度）和最大值（最高溫度）.

（1）求這段時間的最大溫差；

（2）寫出這段曲線的函數解析式．

教師教學用書給出的解答：（1）由題中圖2可知，這段時間的最大溫差是30-10=20（℃）.

二、問題探究

1.φ有沒有取值范圍

φ有沒有取值范圍？φ的取值范圍是什么呢？筆者查閱了普通高中教科書（人教A版）和普通高中教科書（人教B版），以及相應的教師教學用書，對于φ的取值范圍都沒有明確規定，深感失望.筆者從另一個角度出發，對教材中求解析式的習題進行統計，如表1所示，來尋找φ取值范圍的蛛絲馬跡.

由表可知，人教A版、人教B版、北師大版和蘇教版普通高中教科書涉及求解析式的問題共18題，給出取值范圍有7題，約占38.9％，都是根據函數的圖像求函數的解析式；沒有給出范圍的有10題，約

由于例1和習題第8題沒有給出取值范圍，得到了兩種截然不同的正確結果.在給出范圍且區間長度為2π的習題中，都會產生增根，原因在于在已知三角函數值求角，在一個周期內一般總有兩個解.只有在有限的范圍才能得出一個解.

2.求φ值有沒有通性通法

對于φ值的求法，有多種雜志都刊載了這方面的文章.如文［2］中，逆用“五點法”確定初相φ的值；文［4］中，給出了單調性法、最值點法和五點法求φ的值；文［5］中，介紹了最值法、五點法、單調性法和平移法；文［6］中，指出非最值點+單調性、最值點法和五點作圖法是正確求解初相φ的必由之路.歸納起來，求φ值的主要方法有四種：非最值點+單調性、最值點法、五點作圖法和平移法.其中，單調性法（非最值點+單調性）、最值點法、平移法與五點作圖法有內在的聯系，非最值點和最值點都是五點中的某個點，而平移法需要先判定起始點.筆者根據多年的教學實踐，五點作圖法學生最容易接受，解題過程比單調性法、最值點法簡便，且答案唯一，準確率較高，比平移法思路更清晰.因此，我們認為，解決求解正（余）弦型函數解析式或相關的問題，五點作圖法最簡便，可謂是通性通法.

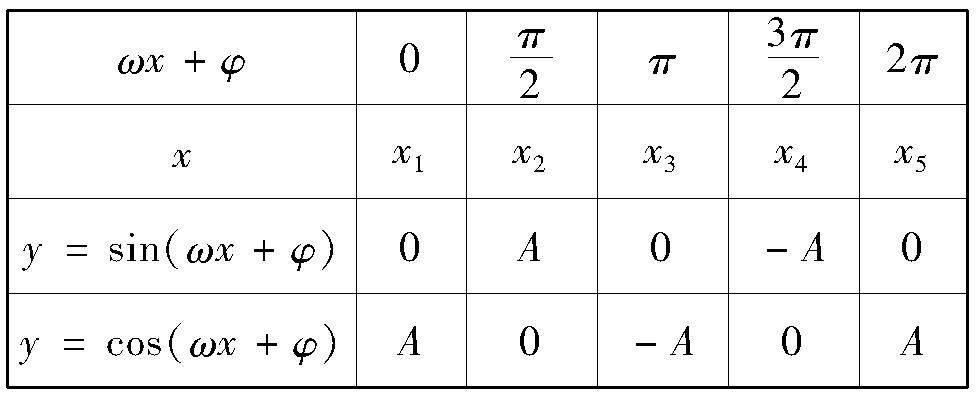
我們通常用“五點法”作函數y=Asin（ωx+φ）或y=cos（ωx+φ）（A＞0，ω＞0，0＜｜φ｜＜π）在一個周期上的圖像.

逆用“五點法”的關鍵是辨清起始點，即點P1，起始點清楚了，問題中已知點對應五點中的第幾點便一目了然.這是一個難點，要向學生講清楚，學生要深刻體會，真正理解.

正弦型函數圖像的起始點就是與x軸的交點，位于y左側或右側，距離y軸最近且處于單調上升曲線中的點.從起始點向右，依次是第二個點（最大值點），第三個點，第四個點（最小值點），第五個點.

余弦型函數圖像的起始點就是最大值點，位于y左側或右側，距離y軸最近的點.從起始點向右，依次是第二個點，第三個點（最小值），第四個點，第五個點（最大值點）.

弄清楚已知點對應五點中的第幾點后，將該點的橫坐標代入ωx+φ，解方程即可求出φ的值.

下面列舉數列予以說明.

由此可見，逆用“五點作圖法”可以作為求解函數解析式以及相關問題的通性通法，既避免了代入平衡點產生增根的弊端，又簡化了代入最值點的解題過程，還克服了平移法中平移方向左、右不清和平移量不準確的錯誤.因此，在平時的教學中，要優化精選習題，提高練習的有效性，掌握核心概念和通性通法，不僅可以培養學生“發現和提出問題，分析和解決問題的能力”，還可以培養學生的數學運算、直觀形象、數學建模等數學核心素養.

參考文獻

［1］中華人民共和國教育部.普通高中數學課程標準（2020修訂版）［S］.北京：人民教育出版社，2020：93.

［2］翟洪亮，杜惠平．逆用“五點法”確定初相φ的值［J］．數學通訊，2023（4）：37-41．

［3］汪繼波．初相角有沒有取值范圍［J］．中學數學雜志，2013（7）：63-64．

［4］郭守虎．消除求初相φ的誤區［J］．高中數學教與學，2018（8）：12-13．

［5］張惠．例談函數y=Asin（ωx+φ）的初相的確定［J］．中學數學，2021年1月．

［6］秦文波．求解初相φ的錯解辨析和模型建構［J］．中學生理科應試，2023（2）：14-16．