大語言模型的會計垂域推理能力探究

鐘慧 陳宋生 王明

【摘要】大語言模型（Large Language Models， LLMs）目前正在重塑各行各業的學習方式、 思維模式和研究范式。如何使 LLMs 與行業結合、 重構 LLMs 與行業的關系， 是推動企業數字化變革和社會發展的重要命題。要實現LLMs在垂域發揮重要作用， 最重要的是提升LLMs的推理能力。本文以如何提升LLMs在會計領域的推理能力為起點， 提出會計垂域推理能力的概念、 研究路徑、 評測標準， 分析中文開源模型清華智譜的GLM 系列的評測結果， 為后續的推理研究提供標準范式， 并為如何提升會計推理能力提供評價標準， 力圖推動LLMs在會計領域達到應有水平。同時， 為驗證LLMs的會計推理能力， 本文比較了GLM-6B、 GLM-130B、 GLM-4 在算術推理能力和會計常識推理能力方面的差別， 并將 OPENAI 的 GPT-4作為基準進行分析。結果表明， 在不同推理提示工程下， 模型規模顯著影響推理能力， 雖然各種模型算術推理能力已經得到極大的提高， 但是會計推理能力還遠不能達到應用水平， 需要在應用中逐層優化， 研究為LLMs會計垂域進入應用實踐的優化過程提供參考。

【關鍵詞】大語言模式；垂域模型；推理能力；提示詞工程；會計推理能力；基準數據集

【中圖分類號】 TP18；F231? ?【文獻標識碼】A? ? ? 【文章編號】1004-0994（2024）11-0017-9

一、 引言

隨著人工智能領域的發展， 人工智能技術［例如大數據、 超級計算、 腦傳感、 大語言模型（Large Language Models，LLMs）等特別是通用自然語言模型， 越來越受到理論界與業界的關注， 他們期望利用人工智能技術驅動社會走向智能化。人工智能儼然已經成為新一代科技創新和產業變革的核心驅動力、 國家和社會創新發展的核心動力、 產業轉型發展的核心支撐力， 以及提升國家競爭力、 維護國家安全的重要內容。2017年7月， 國務院印發《新一代人工智能發展規劃的通知》， 將人工智能作為一項重要發展目標， 力圖構筑我國在人工智能領域的先發優勢， 推動人工智能的跨學科探索性研究， 將人工智能與數學、 神經科學、 量子科學、 社會學、 經濟學等交叉融合， 推動關鍵技術的跨領域運用， 服務于社會各個領域。2023年7月， 國家網信辦等七部門聯合公布《生成式人工智能服務管理暫行辦法》， 鼓勵生成式人工智能技術在各行業、 各領域的創新應用， 鼓勵生成式人工智能算法、 框架、 芯片及配套軟件平臺等基礎技術的自主創新。

在人工智能與LLMs的浪潮下， LLMs技術更新迭代， 模型能力不斷加強， 逐漸形成從底層算力、 模型開發到行業深度應用的全新智能產業。隨著通用LLMs在垂域的發展， 如何使通用LLMs從基礎能力下沉到行業縱深領域的具體應用、 釋放企業數字化轉型潛力， 已成為LLMs技術未來發展的重要方向。相較于模型垂域應用， 通用LLMs在數據、 算力、 規模等方面具有較大的優勢。但從實用性和可實現性視角看， 垂域應用有著不可比擬的優勢， 如： 具有更豐富的縱深領域知識， 其通過提示詞工程和微調等訓練方式， 專注于特定的下游任務， 能夠以較低的成本實現高效率運行， 推動LLMs在業務中的具體落地。垂域LLMs在教育、 金融、 醫學、 法律、 數學等方面進行了初步探索（Li等，2023；Zhang等，2023；Wang等，2023；Yang等，2023）， 但目前在會計領域， 未發現訓練有效的垂域LLMs， 也沒有LLMs的垂域應用， 且尚不存在一個公認且有效的測試數據集。研究由此出發。

現有 LLMs與會計結合的實踐應用中， 通常采用兩種方式。第一種是直接使用計算機的思路與框架， 只是把數據換成會計相關語料（Liu等，2023）， 這種應用沒有針對性， 缺乏會計專業視角。第二種是會計人員對 LLMs的應用場景進行設計應用（Tong等，2024）， 由于把通用 LLMs 直接嫁接到使用場景， 缺乏對 LLMs 的原理分析， 無法進行專業優化。這兩種方式都是基于LLMs通用能力進行的， 并未考慮會計領域的特殊性。會計領域涉及眾多數學推導、 判斷和模型公式等， 相對于LLMs 的自然語言生成（Natural Langnage Generation，NLG）和自然語言理解（Natural Langnage Understanding，NLU）能力， LLMs在會計領域的應用應當更偏重LLMs的推理能力（Reasoning）。因此， 現階段LLMs在會計領域的應用， 應將會計專業理解與LLMs 的應用原理相結合， 制作可以評測LLMs會計專業能力的數據集， 且分析測評結果， 為后續優化指明方向。

本文可能的貢獻在于： 第一， 拓展了通用LLMs在會計領域的垂直應用研究。本文梳理了LLMs在邏輯推理、 數學推理、 常識推理、 抽象推理等方面的技術現狀， 分析了這些能力與會計推理的關聯， 為后續研究奠定了基礎。第二， 彌補了會計評測領域數據集缺失的空白。本文構建了一個覆蓋全面、 多樣化的會計常識推理基準測試集， 區別于已有財經領域數據集， 本測試集聚焦會計循環、 財務報表、 會計分錄等核心主題， 嚴格控制題目質量， 全面評估LLMs的會計領域推理能力。第三， 選取了GPT-4、 GLM 等代表性LLMs在自構建測試集上進行評測， 并分析其表現。這一結果對于理解LLMs在會計領域的適用性具有重要參考價值。第四， 探討融合了領域知識、 優化推理策略等提升LLMs會計推理能力的路徑， 為后續研究指明了方向， 有望推動LLMs與會計專業知識的深度融合， 加速智能化會計實踐的落地。

二、 文獻綜述

（一）LLMs 在會計垂域的發展

通用LLMs在垂直領域的發展在醫學和法律領域已嶄露頭角， 這為其在會計領域垂域應用的建設提供了借鑒。LLMs在醫學領域的成功應用（Panagoulias等，2024）集中在醫療圖像診斷方面， 因為圖像有極強的自然科學客觀規律性， 可以被AI識別， 并利用LLMs診斷的自然語言輸出， 提高AI應用的可解釋性， 使其在醫學上的應用比在其他行業有更好的前景。在法律領域的應用上（Chalkidis，2023）， LLMs難以達到應用級別， 原因是法律環境是一個人類環境， 影響因素不穩定， AI對這種人為規律的識別能力較弱， 且法律的解釋權威性是不能假借予LLMs的。會計領域介于醫學和法律之間， 既有相對客觀的經濟規律和穩定的會計準則， 又面臨復雜多變的人類環境， LLMs需要具備更強的能力， 不同于醫學圖像診斷的記憶， 它們需要像人類一樣解釋因果關系， 并具備舉一反三的邏輯推理能力。會計領域非常注重LLMs的推理能力， 尤其是計算推理和會計常識推理能力。本文探討了推理能力的關鍵性， 旨在突破現有會計應用的局限性。現有研究不足主要有：

1. 單純研究推理能力的提升。這種研究致力于提升LLMs的某一項或幾項推理能力（Huang和Chang，2022）， 但是沒有具體涉足會計常識推理能力， 而其整體提升的常識推理能力混進各種專業知識， 并且提升的推理能力只能達到50% ～ 80%的準確度（Li等，2023）， 不能保證會計推理達到理想狀態。此外， 尚未發現專門針對會計推理能力的文獻。

2. 只關心粗放型的語料基礎的預訓練垂域研究。BloombergGPT（Wu等，2023）、 FinGPT（Liu等，2023）等通過訓練語料的專業化和參數規模增大這種萬能方式來解決一切LLMs的能力提升問題， 但是這種方法依靠的是沒有規律的涌現能力， 尚未知其產生機理（Zhao等，2023）。

3. 任務式的LLMs微調研究。這類研究利用微調的方式提升情感分析任務的準確性（Fatouros等，2023）、 回答金融會計知識的準確性（Theuma和Shareghi，2024）、 金融會計文本分類的準確性（Shah等，2023）等， 這些都是自然語言本來就有的任務， 只是語料變成與金融會計相關， 沒有針對會計特有的任務特征——需要計算、 需要會計專業方能理解。

4. 概述式的研究。廖高可和李庭輝（2023）、 歐陽日輝和劉昱宏（2024）調研已有會計領域LLMs的研究情況與應用現狀后發現， 尚未形成會計領域LLMs的研究方法與范式， 更未涉及會計推理概念與能力提升的具體方案。

綜上， 已有會計垂域研究最大的問題是套用自然語言處理的研究方法， 研究會計文檔分類、 問答、 情感分析任務的完成能力， 而未抓住會計專業方向的重點能力——會計推理能力。這種套用掩蓋了LLMs的真實垂域能力。復旦大學的金融 DISC-FinLLM 的研究（Chen等，2023）按照自然語言的任務能力提升方式， 試圖大量使用金融相關語料微調提升金融能力， 但是效果甚微。原因主要是在提升能力之前， 未充分評測LLMs在專業領域缺失的具體能力， 繼而針對此能力進行后續提升方法研究。

（二）LLMs會計垂域推理能力

在 LLMs研究理論中， 模仿人的邏輯形式完成具體的事情， 簡稱推理（Huang和Chang，2022；Yu等，2023）。邏輯推理評測通常由LLMs回答推理問題的準確性來衡量。按照現行LLMs推理能力分類， 可將其劃分為四種推理能力： 邏輯推理、 數學和計算推理、 常識推理、 抽象推理（Sun等，2023；Huang和Chang，2022）。這四類推理能力在會計領域的應用至關重要， 每一個具體的會計應用場景都涉及不同的推理能力。會計領域大量依賴應用邏輯和數學計算能力， 意味著訓練出縝密的推理能力是LLMs應用于會計領域的關鍵。

邏輯推理能力指的是模型基于特定的事實與命題， 依據規則推導出其他命題的能力， 主要包括自然語言推理與論證推理。自然語言推理主要是判斷兩個句子之間的邏輯關系， 例如蘊含、 矛盾或是否相關等， 根據句子語意去判斷真實表達意圖。自然語言推理能力在會計領域發揮著重要作用， 例如它能夠分析財務報告中的敘述， 判斷管理層討論與財務數據之間是否存在邏輯的一致性（是否言行一致）等。論證推理則是評估論證的有效性和結構， 主要是識別論據和結論。論證推理在財務領域的應用體現在投資報告或市場分析方面， 用以評估其論證的合理性和市場走向預測是否基于有效論據。

數學和計算推理（Cobbe等，2021）主要是指LLMs解決數學運算、 邏輯推導以及運用計算機技術解決問題的能力， 包括算術問題求解、 幾何問題求解、 數學證明等。算術求解主要是基于文本描述解決數學問題， 例如從財務報表的敘述中自動提取和計算關鍵財務指標（利潤率、 增長率等）， 以便快速分析推斷出公司的財務健康狀況； 幾何問題求解是理解與解決結合圖形和文本描述的幾何問題， 具體可應用于行業估值中， 例如在評估商業地產價值時， 通過分析其形狀、 大小和位置信息（結合地理信息系統GIS數據）， 計算出潛在的商業利用價值； 數學證明是生成或驗證數學證明的邏輯過程， 在會計領域能夠實現復雜財務模型的驗證和模型的預測， 確保其在邏輯和數學上的正確性。

常識推理（Talmor等，2022）是基于常識和經驗的思維方式， 對事件發展的邏輯進行歸納總結， 得出合理判斷的能力。常識推理包括事件和因果推理、 常識問答等。事件和因果推理是指LLMs理解文本中事件之間的因果關系和順序， 在會計領域的表現也較為多樣化， 能夠分析市場事件如并購、 政策變更等對公司財務狀況的影響； 常識問答主要就是使用常識知識回答問題， LLMs需要懂得會計領域的專有名詞、 行業準則等基本常識性問題， 能夠回答有關財會相關知識， 輔助會計決策。

抽象推理（Hu等，2023）主要是指從抽象的概念出發， 得出普適性規律和認識的推理過程， 主要包括模式識別和分類、 類比和類比推理。模式識別和分類， 顧名思義就是識別分類抽象模式和概念， 在大量數據中識別出異常數據， 適用于公司風險管理與欺詐檢測； 類比和類比推理是在不同概念、 對象或情景之間的類比， 比較不同時點或不同事件的相同特征， 尋找其中的相似性與差異性。

上述計算機推理研究結合會計理論和會計推理教育定義會計推理（Accounting Reasoning）， 這是一個涉及財務和會計信息解讀、 分析與判斷的過程， 它依賴于對財務數據的理解、 評估和應用， 以做出合理的經濟決策。這種推理過程包括識別和分析會計信息的能力、 解釋財務報表中的數據， 以及將這些信息用于預測、 評估和制定策略。

（三）數據集評測基準

在自然語言處理（Natural Language Processing，NLP）發展初期， 通用LLMs的評測主要是使用簡單基準測試， 評估集中于語法與詞匯等， 包括句法分析、 詞義消歧等任務。隨著深度學習的出現， NLP擁有更加廣泛的基準， SNLI（Bowman等，2015）和SQuAD（Rajpurkar等，2016）這些基準測試不僅能夠評估模型的系統性能， 而且可以提供足夠的訓練數據， 以便于評估特定任務的準確性。隨后， 大規模預訓練語言模型的崛起， 例如BERT模型（Devlinet等，2019）， 使得LLMs的測評方法逐漸演變為適應這些新型通用模型的性能評估方法。如今越來越多的開源基準數據集用于評測LLMs對各項任務的應對與挑戰， 這些測試基準包括但不限于GLUE（Wang等，2018）、 SuperGLUE（Wang等，2019）和 BIG-Bench（Srivastava等，2022）。隨著語言模型規模的不斷擴大， LLMs在零次學習和少量學習的設置下都表現出顯著的改進， 可以與微調的預訓練模型相媲美。這一轉變促成了評估領域的轉變， 標志著從傳統以任務為中心的基準轉向關注以能力為中心的評估。隨著這一趨勢的發展， 設計用于知識、 推理和各種其他能力的評估基準的范圍已經擴大。這些基準的特點是放棄訓練數據， 并制定總體目標， 即在零次學習（Zero-shot）和少次學習（Few-shot）設置下全面評估模型的能力（Zhong等，2023；Zhang等，2023；Li等，2023）。

相比于通用LLMs， 垂直領域應用以其實用性及可實現性等優勢， 備受學術界和業界的關注。它具有更豐富的縱深領域知識， 能夠回答更加專業的問題， 推動LLMs在業務中的具體落地。它專注于特定的下游任務， 通用LLMs的測試基準已不完全適用于LLMs的垂域應用評測， 故需要引入一系列專門的基準測試評估 LLMs在特定領域和應用程序中的能力（Chang等，2023）。對于專業領域評測基準， CMMLU、 GAOKAO Benchmark、 MATH、 APPS、 CUAD、 CMB、 CFBenchmark 等任務與數據集已在中文、 教育、 數學、 計算機、 法律、 中醫、 金融等專業領域建立起基準測試（Li等，2023；Zhang等，2023；Wang等，2023；Yang等，2023）， 這些專業領域的基準能夠很好地評測模型在專有領域的能力， 也能夠通過基準數據集的建立構建其專有領域的垂直模型。

對于評測基準而言， LLMs的評測數據集涉及多個方面多項任務（例如 CLUE 中文理解評估基準有九項自然語言理解任務）， 但內容大多較為寬泛， 給出的答案往往是大眾化、 普適化的內容。通用模型強調的是全方位、 多層次的應對能力， 它對各個專業層次都有應對能力， 但應對復雜情況的處理能力較弱。對于LLMs的垂域評測方式， 以 DISC-FinLLM（Chen等，2023）模型為例， 該模型作為基于多個專家微調的財務金融LLMs， 通過微調形成垂直運用能力， 其主要評估方法包括四個組成部分： 財務NLP任務、 人員測試、 數據分析和實時分析。為評估這四部分能力， DISC-FinLLM模型通過爬蟲、 開源數據集等完成其財務NLP任務、 實時分析任務， 通過自建數據集方式實現數據分析任務（Wang等，2023）。同樣的， BloombergGPT（Wu等，2023）在金融領域特定任務和通用任務兩方面對模型進行整體評估。對于金融領域特定任務的評估， 數據是來源于開源數據集與彭博社專有的內部數據集； 對于通用任務的評估， 通過對BIG-Benchmark等基準數據集的提取與評估得出最終結果， 評估數據集來自HELM、 SuperGLUE、 MMLU和GPT-3等開源的評估基準（Lu等，2023）。

對于模型垂域評測來說， 通用LLMs的評測基準仍適用。LLMs垂域應用需要一定的通用能力， 但對于專業縱深能力來講， 需要建設自有數據集來進行訓練。對于LLMs的垂域建設， 各個專業領域已有布局和建設。以LLMs的會計垂域為例， LLMs垂域評測基準存在一些不足之處： 一是LLMs并無一個固定的會計垂域測評基準， 大多是自建基準或自建數據集， 這在一定程度上降低了垂域評測的可信度； 二是相較于通用LLMs， LLMs在會計垂域處理長文本內容的性能上存在差異， 它們的性能隨著上下文長度的增加而顯著惡化（Bai等，2023）； 三是模型的規模與模型精度之間存在正相關關系， 垂域應用要確保精度， 必須使用高質量數據（Liu等，2023；Li等，2023）， 通用模型測評基準不能完全有效評估模型垂域能力。

LLMs向垂直領域遷移的趨勢日趨明顯， 如何在盡可能保留模型通用能力的同時提高模型在垂直領域的能力一直是熱門話題。會計領域垂域應用的建立， 不僅需要進行邏輯探索、 模型的微調與提示， 還需要一個客觀的評測基準， 如果缺失評測基準， 垂域能力則會失去說服力。因此， 需要建立客觀的數據集測評已有或未來的新模型的會計能力。通過模型的評測得分判斷垂域LLMs是否能夠應用于實際會計場景， 為后續模型的優化提供借鑒。

三、 實驗設計與結果

（一）實驗設計

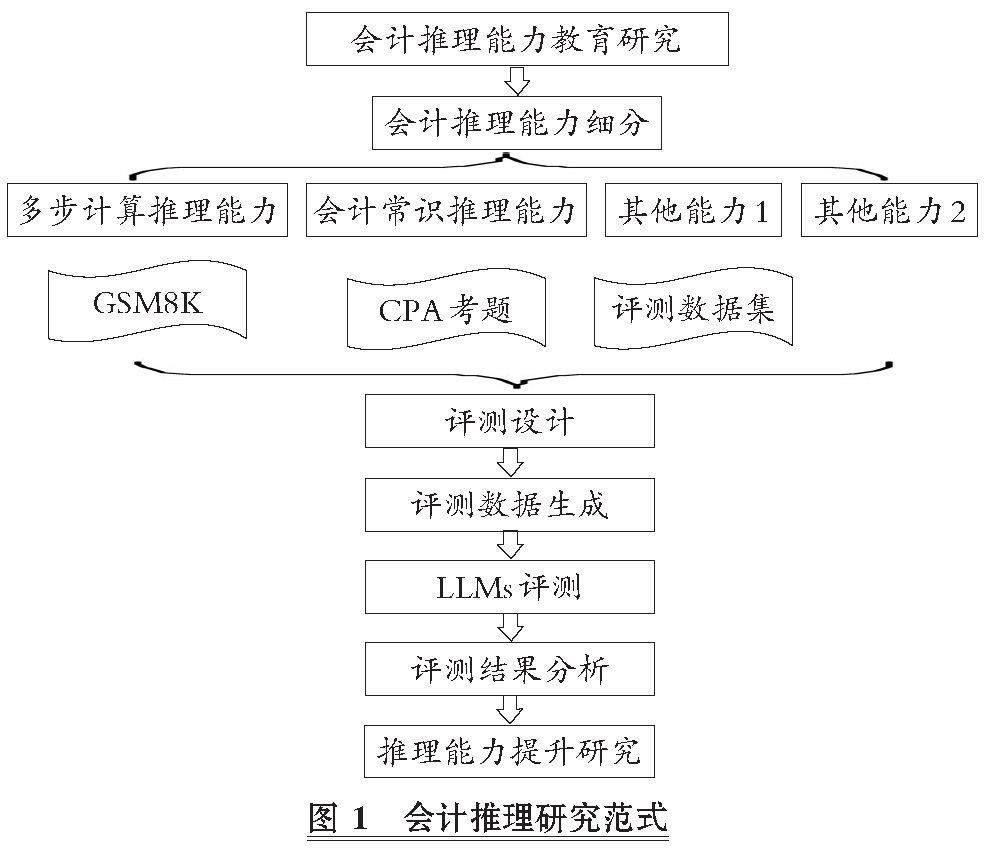
本文創新了LLMs會計推理能力研究范式（見圖1）。首先根據會計教育內容與推理定義理論， 抽象出細分會計推理能力； 然后對每一種細分能力進行評測設計， 包括細分能力的評測方法、 評測可參考的數據集、 評測體系設計； 接著根據評測設計生成測評數據集； 最后進行測評并生成測評結果分析， 根據測評結果提出提升評測能力的方法。

借鑒會計教育方法， 把LLMs當成一個已經有一定會計基礎的學生進行專業教育， 首先需要評測LLMs的會計水平， 定位其缺失的會計內容， 比如折舊方法使用不當、 經營現金流組成部分理解錯誤、 計算錯誤等， 再根據錯誤的內容進行處理。在處理過程中， 如果需要數據進行微調或者上下文提示工程設計， 則要根據具體錯誤內容生成相關性大數據。斯坦福大學陳丹琦團隊的研究表明， 使用精選過的5%數據比原來100%數據微調模型能產生更佳的效果（Xia等，2024）， 精選過的數據集能夠使用高度與提升能力相關的數據， 精準地優化LLMs的會計推理能力。因此， 會計推理能力研究的第一步是準確評測出LLMs會計推理能力的具體缺陷。這需要會計教育分析歸類， 把會計推理能力細分， 然后再進行評測方法研究。

為了不與計算機通用推理能力重合， 可以對跨級推理能力進行分類： 多步計算推理能力、 會計常識推理能力、 會計模式識別能力、 會計類比能力。其中， 多步計算推理是為了迎合會計分析中經常出現復雜連貫的計算， 會計常識推理能力包括各種會計概念理解、 方法選取、 方法使用能力。對于這兩種能力， 幾乎在一切會計問題上都需要LLMs具備較高的水平。而會計模式識別和會計類比能力在特定場合， 比如預測、 發現規律、 比較分析中會有特殊使用。因此， 多步計算推理能力和會計常識推理能力是基礎會計推理能力， 而其他能力是適用于不同應用場合的特殊會計推理能力。本文以基礎會計推理能力的評測為主。

在評價LLMs的推理能力時， 常用準確性來衡量。在會計和審計領域， 對推理能力的衡量除準確性外， 還需要推理過程具有可解釋性， 便于人類理解復雜過程得出的結果是否符合經濟原理或者人類目標。到目前為止， 尚未有LLMs在各項推理任務中都能達到100%的準確率， 但是部分已經達到人類水平。提高各種LLMs在各種推理任務中的完成準確率， 是目前推理研究的目標， 也是會計垂域LLMs真正應用于實踐的關鍵， 但甚少學者研究推理過程的可解釋性。因此， 本文設計一個推理過程， 讓LLMs在利用財務常識計算推理解決問題時， 提供一個可解釋的過程， 并提高計算準確性。

（二）多步計算推理能力評測標準

已有許多評測基準（Benchmarks）用以評測LLMs的通用推理能力［如表1所列（Srivastava等，2022；Yu等，2023；Chang等，2023）］， 這些評測基準一般是自然語言推理任務使用的公共數據集， 數據集中是測試某種推理能力的題目， 并且附有答案， 用來快速檢測LLMs在回答這些題目時的準確率， 包括邏輯推理、 常識推理、 數學推理等， 通過在不同類型的推理任務上測試模型來評估其推理能力。評測中文會計推理能力， 需要中文領域的評測基準， 特別是評測會計常識推理能力時， 如果使用外文的評測基準會使得評測錯誤率由于翻譯錯誤的存在而被高估。多步計算推理能力由于題目語言表達比較簡單， 翻譯錯誤率極低， 可以以數學和計算推理中的評測基準作為參考， 生成新的評測標準。

在計算推理基準數據集中， 最適合評測會計多步計算推理能力的數據集是GSM8K（Cobbe等，2021）， 它是一個包含8.5K個高質量、 語言多樣性的小學數學文字題目的數據集。該數據集旨在支持需要多步推理的基礎數學問題的問答任務。這些問題需要2 ～ 8步解決， 解決方案主要為使用基本算術運算（+、-、×、÷）執行一系列基本計算， 以得出最終答案。一位聰明的中學生應該能夠解決每個問題。問題不需要超出早期代數水平， 絕大多數問題可以在不明確定義變量的情況下解決。以自然語言提供解決方案， 而不是純數學表達式， 是最普遍有用的數據格式。香港中文大學對GSM8K進行改進， 生成的 MR-GSM8K（Zeng等，2024）挑選原數據集中的應用題部分， 把題目分成順向和逆向兩類， 逆向是需要通過設未知數解方程的題目， 順向是按照思路計算即可得到最終答案的題目。在會計知識中， 排除模型分析計算， 大多數計算處于小學數學水平， 涉及日期計算、 多步串聯計算時需要確保LLMs可以記住前面的計算結果， 以將其使用于后續步驟。因此， MR-GSM8K 的順向題目非常適合會計多步計算推理能力評測。MR-GSM8K是目前最常用的計算邏輯測試數據集， 在多種LLMs評測中被列為首選評測基準， 多年的測試經驗證明了其測試計算邏輯的可靠性。過濾掉MR-GSM8K中的逆向題， 再把答案字數少于 300字的題目也過濾掉， 剩下的題目就是分析步驟比較長（3步以上）且計算形式與一般會計計算相近的題目。最終， 剩下586條長計算步驟的MR-GSM8K題目， 其可以作為會計多步計算推理能力的基準數據集， 稱為Multi-Calculation-Benchmark。以下是會計多步計算推理能力基準數據集中的例子：

題目： 杰西卡正試圖計算她每個月需要支付的所有債務總額。她的學生貸款最低還款額為每月300美元， 信用卡的最低還款額為每月200美元， 而她的按揭貸款最低還款額為每月500美元。如果杰西卡想支付比最低額度多 50% 的金額， 她一年內需要支付多少錢？

（三）中文會計常識推理能力評測標準

中文會計常識推理評測基準有兩部分來源： 一是從英文評測基準翻譯而來； 二是通過原生中文會計常識推理任務標注或者爬取取得。相比于多步計算推理能力的評測， 中文會計常識推理能力有顯著的區域差異， 國內外使用的會計準則的差異， 導致國外的會計評測基準不能被直接使用， 而一般的原生評測基準是從通用常識推理 基準數據集中篩選出會計相關的數據作為評測基準。中文語言理解評測基準CLUE（Chinese Language Understanding Evaluation）（Xu等，2020）是一個面向中文的類似于GLUE（General Language Undersanding Evaluation）（Wang等，2018）的語言理解基準， 它旨在評估和提高中文自然語言處理模型的性能。CLUE包括一系列不同的任務， 如文本分類、 閱讀理解和命名實體識別、 推理任務等， 這些任務涵蓋語言理解的各個方面。通過這些任務， CLUE能夠全面評估中文處理模型能力， 并推動中文自然語言處理技術的發展。而由 CLUE 衍生出的推理數據集有以下幾種：

第一， CMNLI 自然語言推理數據集。該數據集內容來自fiction、 telephone、 travel、 government、 slate等， 通過對原始英文MNLI 和XNLI數據翻譯得到。該數據集可用于判斷給定的兩個句子之間是屬于蘊涵、 中立還是矛盾關系。數據集例子如下：

題目： 在這項任務中， 給你一對句。你的工作是選擇這兩個句子是否明確一致（蘊含）/不一致（矛盾）， 或者是否無法確定（中立）。你的答案必須是數字 0（蘊含）、 1（中性）或 2（矛盾）的形式。句子 1： 是的， 我告訴你， 雖然如果你去給那些網球鞋定價， 我明白為什么你現在知道它們的價格在 100 美元的范圍內了。句子 2： 網球鞋有一系列的價格。

第二， OCNLI 中文原版自然語言推理數據集。原生中文自然語言推理數據集 OCNLI是第一個非翻譯的、 使用原生漢語的大型中文自然語言推理數據集， 與CMNLI 具有相似的推理任務， 數據集例子如下：

題目： 在這項任務中， 給你一對句。你的工作是選擇這兩個句子是否明確一致（蘊含）/不一致（矛盾）， 或者是否無法確定（中立）。你的答案必須是數字 0（蘊含）、 1（中性）或 2（矛盾）的形式。句子 1： 因為營業額上升了、 看來， 擴銷的目標有可能實現。句子 2： 營業額上升了。

第三， 螞蟻金融語義相似度數據集（AFQMC）。AFQMC數據集與 OCNLI 一樣， 這些基準數據集提取出來的會計數據集可以評測出LLMs對語言表達相似度的推理能力， 確定LLMs對語言結構、 詞匯通用概念的理解。大規模中文金融領域語料庫BBT-FinCorpus（Lu等，2023）、 CFBenchmark（Lei等，2023）這兩個金融專業數據集注重一般自然語言任務， 如實體命名識別和分類等， 沒有結合會計的專業分析推理， 不能評測LLMs對會計專業概念的理解、 方法的使用能力。DISC-FinLLM 的語料（Chen等，2023）雖然涉及會計分析推理， 但是只涉及少數概念識別， 極少有方法評測。FinEval（Zhang等，2023）是一個真正意義上評測會計常識推理能力的基準數據集， 在會計常識上只有120道題目數據， 并沒有系統覆蓋會計學科理論上的大部分章節， 計算題只占1/4不到， 大部分是簡單的概念識別， 不涉及會計分析方法。數據例子如下：

題目： 哪個選項符合債務重組準則的會計處理要求。

A. 債務重組中涉及的債權、 重組債權、 債務、 重組債務和其他金融工具的確認、 計量

B. 通過債務重組形成企業合并

C. 債權人與債務人在債務重組前后均受同一方或相同的多方最終控制， 且該債務重組的交易實質是債權人或債務人進行了權益性分配或接受了權益性投入

D.以存貨清償債務

計算題可以很好地評測出LLMs對會計概念的理解以及方法的使用是否已經達到類人類理解的階段， 而不僅僅是記憶體能力。全面覆蓋會計知識點才能評測LLMs的會計常識推理能力的問題所在。因此， 以上評測基準并不能很好評測LLMs的專業會計能力， 并找出其問題。比較好的評測方法是使用會計考試題作為評測標準， 其可以滿足知識點覆蓋問題， 以及評測LLMs對概念、 方法的理解。使用入學考試或者學校專業考試（Cheng等，2023）的題目雖然可以從非常基礎的會計知識變化到更高級的知識， 但是它們不一定直接與成為一名執業會計師所需的知識相關聯， 不能評測LLMs的實踐能力。

本文通過使用專業認證考試題目來評測 LLMs 的會計常識推理能力。個人在某一專業認證考試的通過往往代表著個人在該領域有著足夠的認識與理解。只有大語言模型通過專業資格考試， 才能說明其具有某一行業的入門能力。 因此， 大語言模型通過會計專業認證能力測試是其在財會垂域應用的基礎。中國注冊會計師（CPA）考試共有六個科目， 據此可把會計常識推理能力劃分成對應的六個細分（會計、 審計、 稅法、 財務管理、 經濟法和戰略）。

本文以會計常識推理能力為例， 構建評測 LLMs 對應推理能力的數據集。在會計能力考試中， 相較于職稱考試， CPA考試的國際認可度更高、 專業范圍更廣， 能夠適用于多種財經行業的高級職位。因此， 采用CPA會計科目考試題目中的計算題作為基準數據集， 題目覆蓋CPA 考試大綱的各個章節， 包括30章113節知識點內容， 涉及會計分錄借貸判別、 科目選擇、 金額計算、 會計準則適用、 會計概念理解、 方法適用等共404題， 稱為Accoun-ting-Reasoning-Benchmark。評測題目的答案使用的是直接計算結果， 而不是選擇題項目， 原因在于： 研究發現， 某些LLMs在做選擇題項目時會有選項傾向， 而某些 LLMs 即使分析錯誤， 也會進行反復反省， 直到得出一個可選項為止， 這會導致評測失敗。數據例子如下：

題目： 2×17年12月30日， 綠地公司購入一項設備， 支付買價498 萬元， 另支付運輸費2萬元。該項固定資產預計使用年限為10 年， 綠地公司采用直線法計提折舊， 預計凈殘值為零。2×20年12月31日， 綠地公司對該項資產進行減值測試。在確定其公允價值時， 綠地公司根據相關信息得知市場上在1個月前有相關交易發生， 成交價為500 萬元， 成新率為100%。已知該項設備的成新率為60%， 2×20年12月31日綠地公司確定該項設備的公允價值為（）。答案： 300萬元 解析： 確定該設備公允價值時， 按照市場上成交價計算， 由于獲取的信息中成交價對應的成新率是100%， 而綠地公司購入的資產本身成新率為60%， 所以其公允價值應按照成交價乘以成新率來確定。綜上， 綠地公司該項設備的公允價值=500×60%=300（萬元）。涉及知識點： 公允價值概述 難度： 容易 是否真題： 否

對數據集的難度進行定義， 數據集難度界定涉及章節的難度以及計算步驟和邏輯的難度， CPA考試會計計算題章節難度如下（從難至易）： 合并報表—長期股權投資與合營安排—金融工具—收入—租賃—所得稅—股份支付—或有事項—政府補助—企業合并—會計政策、 會計估計—其他章節。根據計算難度和步驟界定如下： 難： 計算步驟較多（>3）或章節較為困難， 或人類正確率較低； 中等： 計算步驟中等（2 ～ 3 步左右）， 章節難度適中； 普通： 計算容易（1 ～ 2 步）， 章節簡單； 容易： 計算容易， 一般一步解決。

在覆蓋CPA考試大綱的30章內容中， 會計教授按照考點及知識點選取了真題和模擬題， 答案選用真題匹配答案和適用頻率高的刷題APP模擬題答案， 并讓擁有CPA《會計》科目及格資格的人員復核答案。題目選取后， 進行基本的清潔流程， 把重復性題目和冗余題目清除。

本文沒有確切預測LLMs在上述考試中表現如何的依據。但從Eulerich等（2023）的研究結果來看， 它應該能夠回答一些問題。預期GPT-4和GLM-4比小規模參數模型如GLM-6B表現得更好。

（四） 評測實驗結果分析

實驗以閉源模型 OPENAI的GPT-4模型評測為基準（Baseline）， 比較清華智譜開源模型 GLM-6B、 GLM-130B、 GLM-4 的測評結果。測評過程中， 使用思維鏈（Chain of Thought，CoT）（Wei等，2022）， 也就是讓LLMs在解答過程中把詳細分析過程輸出， 增加模型的分析能力， 便于最后評測結果分析模型的錯誤原因。同時， 使用Few-shot- Learning（Yu等，2023）方法， 在輸入題目的同時， 給予LLMs三個具體分析解答的例子， 讓其可以學習如何解題。實驗過程如下：

首先， 在上下文提示詞工程階段， 對Zero-shot、 CoT、 Few-shot-CoT分別進行抽樣題目的測試， 在CoT和Zero-shot測試過程中， 發現最終輸出結果混亂， 比如最終結果沒有明確表明、 語言會中英混合、 如有反思階段會循環進行直至達到上下文長度限制。因此， 為了在檢測結果時能夠使用LLMs進行簡單的答案對比判斷， 降低檢測人工成本， 利于檢測結果的推廣， 本文采用Few-shot-CoT進行。同時， Zero-shot對復雜多步的問題的測試準確率極低， 在抽樣中， 計算題的準確率只有Few-shot-CoT的50%不到， 在會計常識測試抽樣中更是達到了僅有的個位數準確率， 沒有發揮出LLMs的潛在能力。因此， 建議在所有的會計垂域應用中， 使用Few-shot-CoT作為上下文提示工程標準。本文的Few-shot-CoT僅選用三個GSM8K未入選題目的CoT例子作為CoT展開模式， 計算過程與輸出最終結果的示例如下：

仿照例子的做法， 逐步地思考， 并給出題目的答案。請嚴格按照例子的輸出格式， 在推理最后###答案： 處給出數字答案＼n例子： ＼n問題1： 一位電子產品銷售員以每臺700元的價格購買了5部手機， 并用價值4000元的鈔票付款。銷售員需要找回多少零錢？＼n 逐步思考： ＼n步驟1： 銷售員購買5部手機， 每部700元， 總共5×700 =[$]<<5×700=3500>>3500元。步驟3： 銷售員需要找回4000-3500 =[$]<<4000-3500=500>>500元的零錢。＼n###答案： 500＼n＼n

然后， 使用LLMs對數據集問題進行批量解決， 形成LLMs的輸出結果Responses。

接著， 以題目的正確答案Truth為基準， 讓GLM-4扮演會計閱卷教師的角色， 把每道題目的Responses作為學生答題答案， 讓GLM-4做出答題是否準確的判斷。

最后， 統計答題的準確率。

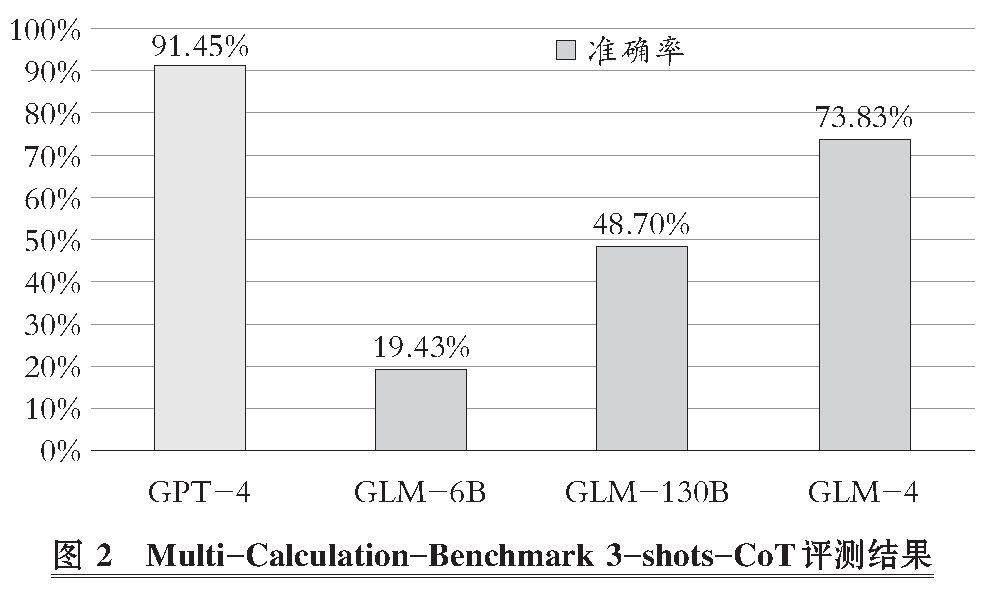
對LLMs進行Multi-Calculation-Benchmark評測， 結果如圖2所示。

GPT-4是其他LLMs評測的基準， 直至2024年2月， 其在普通推理能力中仍然處于第一梯隊， 相當于LLMs的標桿。開源模型在進行測評時， 對照GPT-4的表現， 分析開源模型的差距， 并且在后續改進中， 以基準為優化目標。從評測結果看， 多步計算推理能力在小規模參數如GLM-6B模型（60億參數）LLMs中表現極差， 只有20%不到的準確率， 與基準的差距過大， GLM-6B模型的多步計算推理能力遠達不到人工相比的及格率60%， 而會計對運算要求更高， 要達到90%以上， 才能滿足會計應用的要求。同樣是千億級別的LLMs， GLM-130B、 GLM-4和GPT-4也有明顯差距， GLM-130B雖然有涌現能力的參數規模， 但是準確率還沒達到人類及格線。這種低準確率LLMs在有計算場景的應用上沒有可行性， 嚴重影響分析結果。因此， GLM-6B和GLM-130B不適合獨立使用進行會計分析。

只對多步計算推理能力評測效果優良的GPT-4和GLM-4進行Accounting-Reasoning-Benchmark評測。由于這個Benchmark是由計算題組成， 多步計算推理能力會極大地影響其評測。在相同的會計常識推理能力下， 預期GPT-4的評測準確率會高于GLM-4， 但是結果卻相反， 如圖3所示， GPT-4 的準確率只有16.58%， 而GLM-4達到21.78%。總體來說， GLM-4的會計常識推理能力比GPT-4 要強5%。如果考慮多步計算的影響， 這個差距更大。兩個模型在會計常識推理能力上都沒有及格， 離應用還有很大距離， 需要進行后續的調優和改進。GLM-4相對于GPT-4有更優的會計常識推理能力， 從圖3中可以觀察到GLM-4容易難度下的數據集。由于大多只有一步計算， 準確率達到40%， 而其他三種難度的準確率與難度似乎沒有直接的關系， 證明GLM-4的難度表現與人類理解的會計常識難度是不一致的。它會對會計某些獨特的知識點理解較好， 對某些會計方法使用較差， 而不能用人類的會計準確率替代。這三種難度都屬于多步計算的會計常識題目， 因此多步計算推理能力的影響是比較接近的， 對只有一步計算的容易題目影響較少。因此， 去除多步計算推理錯誤的影響后， 后三種難度會有相對較高的提升。進一步提高GLM-4 的會計應用能力， 需要在后續分析GLM-4的會計常識推理缺陷， 進而進行改進。

在普通難度和中等難度兩類題目的準確率上， 出現了與難度相反的關系， 進一步印證了GLM-4在會計常識推理上的難度判定與人類的判定有差距。為了找出這種反差的原因， 本文對這兩種難度的錯題進行了分類統計， 可以把錯誤歸結為六類主要原因：

第一， 會計方法使用錯誤。LLM在分析過程中對相關會計準則或會計處理方法的運用出現偏差或錯誤， 如在特定情況下錯誤地選擇了計量屬性、 未能正確識別需要進行會計處理的事項、 對準則規定的確認條件理解有誤等， 由此導致在中間計算過程或最終答案上出現錯誤。

第二， 知識點掌握不全面。這部分題目中， LLM對題目涉及的部分知識點理解不到位或者遺漏了一些關鍵信息， 從而在分析過程中考慮不周全， 未能全面領會題意。

第三， 題目過于復雜導致難以處理。有一部分題目涉及特別復雜的會計處理或計算， LLM在這類題目上遇到了較大困難， 體現為分析邏輯不夠清晰或者處理方法失當。這可能超出了LLM目前的能力范圍。

第四， 答題邏輯和思路正確但計算出錯。這類題目中LLM對知識點的理解和運用大體正確， 構建了合理的答題邏輯， 但在具體數字計算環節出現了一些失誤。

第五， 知識點理解存在偏差。這部分錯題反映出LLM對一些會計概念或處理原則的理解存在偏差或混淆， 如資產減值準備的計提、 遞延所得稅的確認等。在一些需要綜合考慮多方面因素的問題上， 如或有事項的判斷、 資產減值跡象的識別等， LLM對各因素的權衡不夠到位， 得出的結論有時存在片面或矛盾之處。

第六， 知識應用不精準。LLM雖然對一些會計準則的原理性內容理解較好， 但在具體應用到實務問題時還不夠精準到位， 如現金流量表的編制、 所得稅費用的確認等。同時， 對一些細節的把握也有偏差。這反映出LLM在將理論知識運用到實務的能力上還有待加強。

圖4是兩種難度在六類錯誤原因中的占比， 有些題目錯誤的原因不是單一的， 所以占比總和不是100%。普通難度的題目極少涉及實務， 所以沒有實務錯誤類型。

第一種錯誤特征“會計方法使用錯誤”和第五種錯誤特征“知識點理解存在偏差”有一定的相似性和關聯性， 這兩種錯誤特征都反映出LLM對某些會計知識點的理解和掌握還不夠全面、 準確， 而知識點理解上的偏差很可能會導致會計方法使用上的錯誤。這種對知識的基本識別錯誤占了錯誤比例的50%以上， 而且相對于其他錯誤容易修正， 是一個值得關注的錯誤大類型。但是它們之間又有根本的區別： “會計方法使用錯誤”主要是指在具體運用會計處理方法時出現錯誤， 如錯誤選擇計量屬性、 未正確識別需處理的事項等， “知識點理解存在偏差”主要是指對會計概念、 會計原則等理論知識的理解存在偏差或混淆， 側重于會計理論認知層面； “會計方法使用錯誤”通常表現為在具體的會計處理環節如確認、 計量、 列報等方面出現的錯誤， 在解題過程中易于識別， “知識點理解存在偏差”可能會間接導致會計處理的錯誤， 但更多地體現在分析和論證環節對某些概念的錯誤表述或理解不到位， 有時可能不會直接反映在最終的計算答案中； 在提升難易度和評測精準度上， “會計方法使用錯誤”更有利， “知識點理解存在偏差”的識別需要對比分析， 更難發現。

第二類錯誤“知識點掌握不全面”是GLM-4無論在會計常識推理還是多步計算推理中都會出現的一種常見錯誤， GLM-4會經常遺漏題目影響因素， 這種錯誤與LLMs的本質特點關系更強烈， 需要提升通用能力才能較好地解決。從難度區分上分析， 兩種難度的計算步驟多是2 ～ 3步， 極少出現1步， 因此計算難度比較類似， 計算占比的差異可以歸咎于抽樣誤差， 與GLM-4在兩類題目中計算的差異性無關。第三種錯誤“題目過于復雜導致難以處理”是指對一些特殊或小眾的會計處理如BT項目、 售后租回等準則的了解不夠全面， 對新修訂準則的知識更新也有所滯后， 導致分析不夠周全， 未能全面領會題意。從第二、 三和四種錯誤的占比對比可以看出， 兩種難度的差距并不大， 而且從以上分析來看， 這三種錯誤一般跟題目難度關系不大。因此， 難度與準確度的反差可以歸咎于是第一種和第五種錯誤的反差造成的。而這兩種錯誤的題目難度， 在區分普通和一般時， 是以章節按CPA考試的難易度進行的。可以看出， GLM-4的章節難易度在這個維度與CPA考綱的難易度區分并不完全一致。這是由于大多數LLM內核的難易度是跟訓練語料的常見程度有關， 如果某些CPA章節的訓練語料更常見， 相對來說它就更容易學習到該章節的內容。

四、 結論

本研究探討LLMs在會計領域的應用前景， 通過設計兩個評測基準來評估 LLMs在多步計算推理以及會計專業知識方面的表現。結果表明， 盡管LLMs在通用領域已經取得令人矚目的成就， 但在會計專業領域， 它們的表現還有很大提升空間。具體而言， 當前最先進的LLMs如GPT-4在多步計算推理任務上的準確率最高可達91.45%， 而在會計專業知識任務上的準確率低于22%。通過進一步的分析， 本文探究了LLMs在會計常識推理過程中出現錯誤的主要原因并指出錯誤的六個類型， 分析出各類錯誤在難度分層中的占比及差異， 這也為后續改進指明了方向。

從本文設計的實驗中可以發現， LLMs難以利用訓練中獲得的通用知識來處理會計領域的具體問題。未來研究可以關注以下方面： 一是繼續擴充高質量的會計領域語料， 為 LLMs 提供更多專業知識的學習素材； 二是在通用LLMs的基礎上， 采用領域自適應的微調方法， 使其更好地適配會計場景； 三是探索在會計領域引入外部知識增強方法， 例如利用知識圖譜等先驗知識來指導 LLMs推理； 四是借鑒認知科學和教育學的理論， 優化LLMs的Few-shot學習范式， 提高其快速學習新知識的能力； 五是深度發掘LLMs缺失的會計能力， 從其推理錯誤內容中找尋具體的模型改進方法， 推動六類錯誤的改進。

總之， LLMs在會計領域的應用還處于起步階段， 未來仍需在數據、 模型和評測等多個層面開展研究。通過學界和業界的共同努力， LLMs必將在會計智能化進程中發揮越來越重要的作用。本研究為這一目標的實現提供了重要的理論與實踐參考。

【 主 要 參 考 文 獻 】

廖高可，李庭輝．人工智能在金融領域的應用研究進展［ J］．經濟學動態，2023（3）：141 ～ 158．

歐陽日輝，劉昱宏．生成式人工智能（AIGC）融入制造業的理論邏輯與實現路徑［J/OL］．新疆師范大學學報（哲學社會科學版）：1 ～ 14. ［2024-05-22］.https：//doi.org/10.14100/j.cnki.65-1039/g4.20240016.001．

Chalkidis I.. Chatgpt may pass the bar exam soon， but has a long way to go for the lexglue Benchmark［DB/OL］． https：//arxiv.org/abs/2304.12202，2023-03-09．

Chang Y.， Wang X.， Wang J.， et al.. A survey on evaluation of large language models［ J］． ACM Transactions on Intelligent Systems and Technology，2024（3）：1 ～ 45．

Chen W.， Wang Q.， Long Z.， et al.. Disc-finllm： A chinese financial large language model based on multiple experts fine-tuning［DB/OL］． https：//arxiv.org/abs/2310.15205，2023-10-23．

Chen Z.， Chen W.， Smiley C.， et al.. Finqa： A dataset of numerical reasoning over financial data［DB/OL］． https：//arxiv.org/abs/2109.00122，2021-09-01．

Cobbe K.， Kosaraju V.， Bavarian M.， et al.. Training verifiers to solve math word problems［DB/OL］．https：//arxiv.org/abs/2110.14168，2021-10-27．

Fatouros G.， Soldatos J.， Kouroumali K.， et al.. Transforming sentiment analysis in the financial domain with ChatGPT［ J］． Machine Learning with Applications，2023（14）：100508．

Hu H.， Lu H.， Zhang H.， et al.. Chain-of-symbol prompting elicits planning in large langauge models［DB/OL］．https：//arxiv.org/abs/2305.10276，2023-05-17．

Huang J.， Chang K. C. C.. Towards reasoning in large language models： A survey［DB/OL］． https：//arxiv.org/abs/2212.10403，2022-12-20．

Lei Y.， Li J.， Jiang M.， et al.. CFBenchmark： Chinese financial assistant Benchmark for large language model［DB/OL］．https：//arxiv.org/abs/2311.05812，2023-11-10．

Li C.， Liang J.， Zeng A.， et al.. Chain of code： Reasoning with a language model-augmented code emulator［DB/OL］． https：//arxiv.org/abs/2312.04474，2023-12-07．

Liu X. Y.， Wang G.， Zha D.. Fingpt： Democratizing internet-scale data for financial large language models［DB/OL］． https：//arxiv.org/abs/2307.10485，2023-07-19．

Lu D.， Wu H.， Liang J.， et al.. BBT-Fin： Comprehensive construction of chinese financial domain pre-trained language model， corpus and Benchmark［DB/OL］． https：//arxiv.org/abs/2302.09432，2023-02-18．

Panagoulias D. P.， Virvou M.， Tsihrintzis G. A.. Evaluating LLM--Genera-ted Multimodal Diagnosis from Medical Images and Symptom Analysis［DB/OL］．https：//arxiv.org/abs/2402.01730，2024-01-18．

Shah A.， Paturi S.， Chava S.. Trillion dollar words： A new financial data-set， task & market analysis［DB/OL］． https：//arxiv.org/abs/2305.07972，2023-05-13．

Srivastava A.， Rastogi A.， Rao A.， et al.. Beyond the imitation game： Quantifying and extrapolating the CPAabilities of language models［DB/OL］．https：//arxiv.org/abs/2206.04615，2022-06-09．

Sun J.， Zheng C.， Xie E.， et al.. A survey of reasoning with foundation models［DB/OL］． https：//arxiv.org/abs/2312.11562，2023-12-17．

Talmor A.， Yoran O.， Bras R L.， et al.. Commonsenseqa 2.0： Exposing the limits of AI through gamification［DB/OL］．https：//arxiv.org/abs/2201.05320，2022-01-14．

Theuma A.， Shareghi E.. Equipping language models with tool use CPAability for tabular data analysis in finance［DB/OL］．https：//arxiv.org/abs/2401.15328，2024-01-27．

Wang A.， Singh A.， Michael J.， et al.. GLUE： A multi-task Benchmark and analysis platform for natural language understanding［DB/OL］． https：//arxiv.org/abs/1804.07461，2018-04-20．

Wang Y.， Kordi Y.， Mishra S.， et al.. Self-instruct： Aligning language models with self-generated instructions［DB/OL］． https：//arxiv.org/abs/2212.10560，2022-12-20．

Wei J.， Wang X.， Schuurmans D.， et al.. Chain-of-thought prompting elicits reasoning in large language models［ J］． Advances in Neural Information Processing Systems，2022（35）：24824 ～ 24837．

Wu S.， Irsoy O.， Lu S.， et al.. Bloomberggpt： A large language model for finance［DB/OL］． https：//arxiv.org/abs/2303.17564，2023-03-30．

Xia M.， Malladi S.， Gururangan S.， et al.. Less： Selecting influential data for targeted instruction tuning［DB/OL］．https：//arxiv.org/abs/2402.04333，2024-02-06．

Xu L.， Hu H.， Zhang X.， et al.. CLUE： A Chinese language understanding evaluation Benchmark［DB/OL］． https：//arxiv.org/abs/2004.05986，2020-04-13．

Yu Z.， He L.， Wu Z.， et al.. Towards better chain-of-thought prompting strategies： A survey［DB/OL］． https：//arxiv.org/abs/2310.04959，2023-10-08．

Zhang L.， Cai W.， Liu Z.， et al.. Fineval： A chinese financial domain knowledge evaluation Benchmark for large language models［DB/OL］． https：//arxiv.org/abs/2308.09975，2023-08-19．

Zhao W. X.， Zhou K.， Li J.， et al.. A survey of large language models［DB/OL］． https：//arxiv.org/abs/2303.18223，2023-03-31．