數(shù)學(xué)抽象理解及解題技巧

胡新華

摘要：三角形是具有性質(zhì)特征的最簡單的幾何圖形，盡管圖形是直觀的，但將圖象概括為數(shù)學(xué)概念卻是一個抽象化的過程，因為三角形包含有邊的長短、角的大小等“數(shù)字化”的要素.換句話說是將“形”轉(zhuǎn)化為“數(shù)”的過程，是數(shù)學(xué)概念抽象概括的過程.“探索三角形全等的條件”就是對兩個邊長、角度一一對應(yīng)的三角形，結(jié)合前面學(xué)過的線段和兩角相等的知識進(jìn)行探究，找出它們中一一對應(yīng)的邊、角相等的條件，是數(shù)學(xué)抽象理解與應(yīng)用的過程.因此，在“探索三角形全等的條件”的課堂教學(xué)中，采用“實踐活動中構(gòu)建方法”的探究發(fā)現(xiàn)法最合適不過，既可以激活課堂氣氛，又可以驅(qū)動學(xué)生的探究熱情.

關(guān)鍵詞：三角形全等的條件；抽象理解；解題技巧

“探索三角形全等的條件”是蘇科版數(shù)學(xué)八年級上冊第一章的內(nèi)容，是繼認(rèn)識三角形之后，了解全等圖形和全等三角形之后的知識拓展，體現(xiàn)了抽象的“數(shù)形轉(zhuǎn)換”的數(shù)學(xué)基本思維方法［1］.基于此，在課堂教學(xué)中，教師需要精心創(chuàng)設(shè)適合學(xué)生探究的教學(xué)情境，讓學(xué)生自主在實踐活動中得到原理和結(jié)論，親歷解決質(zhì)疑情境問題的過程，從而構(gòu)建釋疑的方法，并內(nèi)化為解決問題的基本技能、技巧.

1 創(chuàng)設(shè)實踐案例，激發(fā)學(xué)生去思考

有人說“好奇是致勝的魔杖”，的確如此.好奇心強、探索心強是初中生的基本特征，根據(jù)這一點，教師可以創(chuàng)設(shè)能夠吸引學(xué)生眼球的案例，引導(dǎo)學(xué)生存疑，再通過實踐活動探究，找到釋疑的途徑.例如，在“探索三角形全等的條件”的課堂導(dǎo)入環(huán)節(jié)，可以這樣精心創(chuàng)設(shè)情境.

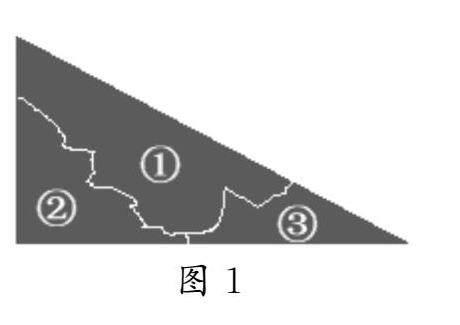
師：教室后面的小組評比欄目需要進(jìn)行周期性清理，然后重新記錄評估，欄目中張貼的小紅旗（紙質(zhì)）不可能完整揭下來，需要重新用紅紙剪裁出相同的小紅旗（三角形）.若某小紅旗揭下來時，撕成下列三塊，你認(rèn)為用其中的哪些碎片就可以重新用紅紙剪裁相同的小紅旗呢？

教師課前給每位學(xué)生分發(fā)小紅旗的碎片，如圖1所示，讓學(xué)生自己剪裁出小紅旗的三塊碎片.

學(xué)生選擇不同的碎片進(jìn)行探究，嘗試?yán)貌煌乃槠蛘咚槠慕M合重新用紅紙剪裁相同的小紅旗.

活動預(yù)案：取①②③中的一塊碎片，不能用紅紙剪裁出相同的小紅旗（三角形），這說明只知道一個角相同時，不能確定兩個三角形全等；取①②③中的任意兩塊碎片無縫對接，都能用紅紙剪裁出相同的小紅旗（三角形）（可以提醒學(xué)生注意，若有縫隙，或者碎片有部分重疊，則情況又會怎樣？），這說明只知道兩個角和其夾的一條邊相同時，能確定兩個三角形全等.

通過活動，教師及時.兩個三角形的兩邊及其夾角相等時即全等，簡稱“ASA”.

創(chuàng)設(shè)目的：“用紅紙剪裁相同的小紅旗”的實踐活動實質(zhì)就是探究三角形全等條件的過程.開展這樣的課堂活動，可以滿足學(xué)生的好奇心和探究知識的欲望，在親歷嘗試的過程中認(rèn)知三角形全等的條件.因此，探究發(fā)現(xiàn)法的是利用學(xué)生的好奇心發(fā)現(xiàn)生成知識的過程，是求知欲的體現(xiàn)，是可以實現(xiàn)的目標(biāo)［2］.

2 設(shè)置經(jīng)典問題，驅(qū)動學(xué)生去挑戰(zhàn)

從八年級學(xué)生的學(xué)情可知，他們對幾何知識的認(rèn)知還是瘠薄的，部分學(xué)生對探究幾何問題的方法、經(jīng)驗不足，達(dá)不到“數(shù)形轉(zhuǎn)換”的思維水平，使得獨立完成數(shù)學(xué)問題的探究成為空中樓閣.為了能讓這部分學(xué)生迎頭趕上，最有效的方法就是在課堂上生成新知之后及時設(shè)置課堂練習(xí)，通過小組合作的形式進(jìn)行探究、交流，在活動過程中領(lǐng)會知識扎實的學(xué)生的思維方法，并內(nèi)化為自己解決數(shù)學(xué)問題的能力.例如，在探索得到“兩邊及其夾角分別相等的兩個三角形全等”后，要求學(xué)生分組探究這一基本事實的具體形式.

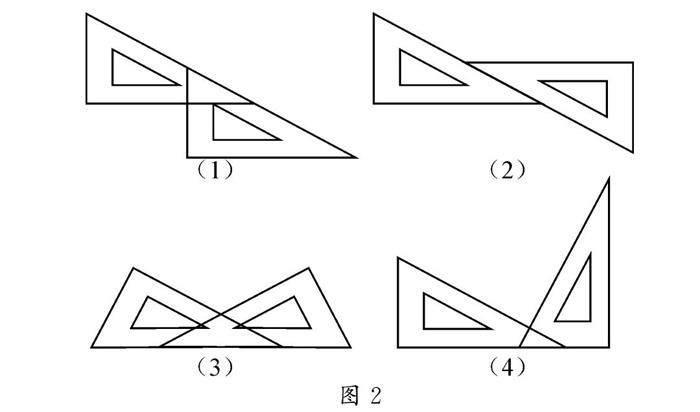
師：請同學(xué)們用兩個相同的三角板，使其一邊緊靠在一起，且不完全重合，觀察這兩個三角板的位置，編寫一道利用本節(jié)課所學(xué)知識證明三角形全等的題，并寫出證明過程.

生：用兩個相同的三角板嘗試滿足教師設(shè)置的問題的要求，可以得出眾多的位置.

活動預(yù)案：常見的兩個相同的三角板位置形式如圖2.

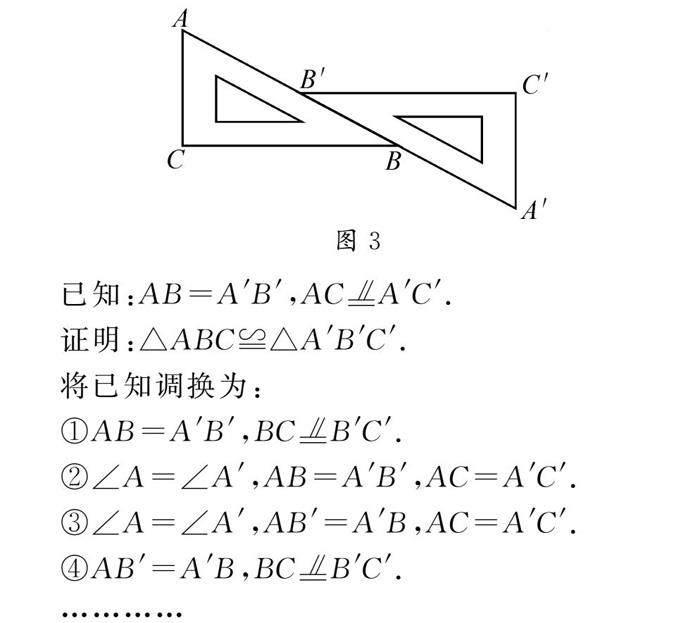
其中，用圖2（2）的形式編寫的數(shù)學(xué)證明題的成功案例如下：

如圖3，在△ABC和△A′B′C′中，A，B，A′，B′四點在同一直線上.

證明過程都是利用課堂學(xué)習(xí)的新知：兩邊及其夾角相等的兩個三角形全等，可以簡稱為“SAS”.

創(chuàng)設(shè)目的：通過用兩個相同的三角板的組合位置，編寫一道利用本節(jié)課所學(xué)知識證明三角形全等的題目的課堂活動是開放性的，因此采用了小組合作交流的方式.因為還未學(xué)習(xí)直角三角形的概念，不用考慮三角板的具體角度.課堂活動中，學(xué)生設(shè)計的兩個三角板的位置是五花八門的，如圖2中的（4），當(dāng)然也可以編寫其他數(shù)學(xué)問題，但已知條件就復(fù)雜得多，對學(xué)生應(yīng)用知識的能力有更高的要求.因此，本活動采用小組合作探究的形式，有利于幫助學(xué)生克服探究過程中出現(xiàn)思維障礙導(dǎo)致無法獨立解決的困難，同時，在合作中內(nèi)化知識、優(yōu)化構(gòu)建、積累方法、激活思維、形成技巧.

3 內(nèi)化生成知識，強化學(xué)生去拓展

課堂上學(xué)生對如何探究知識有了清晰的脈絡(luò)之后，就需要將所獲取的新知進(jìn)行提煉與內(nèi)化，真正了解數(shù)學(xué)問題的奧妙之處，這是課堂教學(xué)的重要環(huán)節(jié)，也是學(xué)生發(fā)展能力、形成學(xué)科素養(yǎng)不可或缺的組成部分.換句話說，就是驅(qū)動學(xué)生充分思考，獲取感悟，深入探究，掌握技能方法.

如，可以采用近年的中考試題來內(nèi)化所學(xué)的新知.

典例 （2021年福建中考題改編）如圖4，已知D是BC的中點，F(xiàn)為AD的延長線上一點，作BE∥CF交AD于點E，求證：BE=CF.

學(xué)生根據(jù)已知條件找到△BED≌△CFD，即可得出BE=CF.

活動預(yù)案：在探究后的展示環(huán)節(jié)中，有學(xué)生給出這樣的證明過程.

在△BED和△CFD中，因為D是BC的中點，故BD=CD；∠EDB=∠FDC；又由BE∥CF，得出∠DEB=∠DFC.所以△BED≌△CFD，故BE=CF.

展示之后有學(xué)生提出異議：本節(jié)“探究出的兩個三角形全等的條件”是“ASA”，而該學(xué)生給出的卻是“AAS”，兩個三角形能全等嗎？

于是，該學(xué)生進(jìn)行反駁：因為三角形的內(nèi)角和是180°，在△BED和△CFD中有兩個角相等，那么，它們的第三個角必定也相等，因此“AAS”也可以作為判斷兩個三角形全等的條件.

創(chuàng)設(shè)目的：在探索問題的時候，初中生時常會力不從心，分類探討時丟三落四是常見現(xiàn)象.因為他們正處于從直觀思維到邏輯思維的過渡期，討論問題時難免會出現(xiàn)思維跳躍等情況.本例旨在引導(dǎo)學(xué)生看問題時要注意養(yǎng)成全面思考的習(xí)慣，不斷提升思維水平，進(jìn)而內(nèi)化成數(shù)學(xué)思維、數(shù)學(xué)能力、數(shù)學(xué)素養(yǎng).

總之，只要在數(shù)學(xué)課堂教學(xué)中做到“創(chuàng)設(shè)實踐案例，激發(fā)學(xué)生去思考；設(shè)置經(jīng)典問題，驅(qū)動學(xué)生去挑戰(zhàn)；內(nèi)化生成知識，強化學(xué)生去拓展”，那么，數(shù)學(xué)抽象理解及解題技巧就會生根于學(xué)生的腦海中，內(nèi)化成自身的素養(yǎng)［3］.

參考文獻(xiàn)：

［1］尚衛(wèi)成，譚曉玲.初中數(shù)學(xué)核心素養(yǎng)“數(shù)學(xué)抽象”理解及解題技巧——以"探索三角形全等條件"為例［J］.數(shù)學(xué)之友，2022，36（23）：34-36.

［2］梁大胤.探索三角形全等條件案例分析［J］.試題與研究（教學(xué)論壇），2021（1）：122.

［3］魏凱，陳捷，張龍娟.基于數(shù)據(jù)采集與分析的課堂互動教學(xué)模式研究——以《探索三角形全等條件》一課為例［J］.中國信息技術(shù)教育，2020（2）：71-74.