基于Pythagorean模糊環(huán)境下MABAC方法的網(wǎng)絡(luò)貨運(yùn)平臺(tái)車貨匹配研究
劉玲 吳瑞東 馬楠 夏露

關(guān)鍵詞:車貨匹配;Pythagorean模糊;反正切Pythagorean模糊熵;MABAC
中圖分類號(hào):F252 文獻(xiàn)標(biāo)識(shí)碼:A 文章編號(hào):2096-7934(2024)05-0083-14
一、引言
網(wǎng)絡(luò)貨運(yùn)依托互聯(lián)網(wǎng)平臺(tái)整合配置運(yùn)輸資源,是一種新興的物流運(yùn)輸服務(wù)模式。網(wǎng)絡(luò)貨運(yùn)由無車承運(yùn)人的概念發(fā)展而來,無車承運(yùn)人早在2013年被提出。我國于2016年正式推行無車承運(yùn)人平臺(tái)試點(diǎn)工作,2019年交通運(yùn)輸部發(fā)布《網(wǎng)絡(luò)平臺(tái)道路貨物運(yùn)輸經(jīng)營管理暫行辦法》正式提出了網(wǎng)絡(luò)貨運(yùn),無車承運(yùn)人試點(diǎn)工作結(jié)束,網(wǎng)絡(luò)貨運(yùn)的發(fā)展逐步走向正規(guī)化和標(biāo)準(zhǔn)化。
網(wǎng)絡(luò)貨運(yùn)平臺(tái)(以下簡稱平臺(tái))的發(fā)展尚處于初級(jí)階段,各網(wǎng)絡(luò)貨運(yùn)平臺(tái)在快速發(fā)展的同時(shí)也面臨許多問題。2022(第五屆)中國網(wǎng)絡(luò)貨運(yùn)平臺(tái)年會(huì)指出我國網(wǎng)絡(luò)貨運(yùn)平臺(tái)面臨惡性競爭問題。一是價(jià)格戰(zhàn),一些企業(yè)為爭奪市場份額,采取不合理的價(jià)格競爭策略,不顧成本和利潤,大幅降低運(yùn)輸價(jià)格,導(dǎo)致整個(gè)行業(yè)的運(yùn)價(jià)水平持續(xù)下滑。二是不正當(dāng)競爭,一些司機(jī)為了爭搶訂單,未考慮自身的運(yùn)營能力,不惜花高價(jià)在平臺(tái)充值會(huì)員獲取訂單,但是在獲得訂單后會(huì)出現(xiàn)貨物送達(dá)時(shí)間延誤、貨物損失率增加等狀況。三是分單不合理,平臺(tái)利用算法單方面制定接單、派單規(guī)則,平臺(tái)推薦的匹配方案不合理,未考慮貨主對于車輛和運(yùn)輸時(shí)效的特殊要求,最終導(dǎo)致訂單無法成交。因此,對于各網(wǎng)絡(luò)貨運(yùn)平臺(tái)而言,探索有效的車貨匹配方法十分必要,這能在保證車主、貨主、平臺(tái)三方利益的前提下,維持整個(gè)行業(yè)的運(yùn)價(jià)水平的相對穩(wěn)定,提高訂單的成交率。
本文試圖通過多屬性群決策方法建立車貨匹配規(guī)則,在保證車主、貨主、平臺(tái)三方利益的前提下解決平臺(tái)間的價(jià)格戰(zhàn)、卡車司機(jī)間的搶單、平臺(tái)推薦匹配方案不合理問題。具體而言,采用Pythagorean模糊數(shù)表示專家評(píng)價(jià)語言,采用反正切Pythagorean模糊熵計(jì)算指標(biāo)權(quán)重和專家權(quán)重,采用Pythagorean模糊愛因斯坦加權(quán)平均(PFEWA)算子計(jì)算綜合評(píng)價(jià)矩陣,運(yùn)用多屬性邊界近似區(qū)域比較(Multiple Attribute Border Approximation Comparison,MABAC)方法對備選方案進(jìn)行排序,給出最佳決策方案。
二、國內(nèi)外研究現(xiàn)狀
近年來,網(wǎng)絡(luò)貨運(yùn)平臺(tái)車貨匹配的研究吸引了眾多學(xué)者的關(guān)注。目前國內(nèi)外學(xué)者的研究多圍繞建立以算法、目標(biāo)函數(shù)、要素為主的數(shù)學(xué)模型開展。牟向偉等學(xué)者引入量子群成熟度改進(jìn)量子進(jìn)化算法的退出機(jī)制,建立車貨供需匹配模型,提高貨運(yùn)供需匹配效率[1];余海燕等學(xué)者將就近隨機(jī)配對算法和滾動(dòng)時(shí)域完美匹配算法分別用于搶單模式和派單模式的車貨匹配中,以解決客戶等待時(shí)間較長、客戶滿意度不高的問題[2];田然等學(xué)者將車輛、貨物、匹配組合和時(shí)間映射到貝葉斯網(wǎng)絡(luò)節(jié)點(diǎn)中,設(shè)計(jì)了基于改進(jìn)的動(dòng)態(tài)貝葉斯網(wǎng)絡(luò)的車貨匹配算法[3]。李建斌等學(xué)者綜合考慮多方限制因素,建立了服務(wù)總成本最小化的車輛路徑優(yōu)化模型,以實(shí)現(xiàn)司機(jī)和客戶雙方利益最大化[4];王寒飛基于考慮車輛類型的貨物對車輛的偏好矩陣和考慮利潤的車輛對每個(gè)貨物的偏好矩陣,建立了以平臺(tái)收益最大化為目標(biāo)的穩(wěn)定車貨匹配模型[5];蔣長兵等學(xué)者提出了一種具有碳稅約束的網(wǎng)絡(luò)貨運(yùn)訂單分配機(jī)制,并建立了一種具有碳稅約束的訂單分配優(yōu)化模型,以解決道路貨運(yùn)行業(yè)中訂單分配不當(dāng)和缺乏碳排放約束系統(tǒng)的問題[6]。朱江洪等學(xué)者基于不確定語言關(guān)聯(lián)性信息,構(gòu)建了綜合考慮主體公平性和滿意度的車貨雙邊匹配決策模型,以提高匹配過程中車貨雙方主體的滿意度[7];張慶瑩從車貨匹配平臺(tái)的角度出發(fā),充分考慮各方主體利益、貨源緊急程度和運(yùn)力資源有效利用率等要素,在貨源時(shí)間窗約束下建立了運(yùn)力資源選擇模型,以解決運(yùn)力資源組織不平衡的問題[8];張青杰等學(xué)者除了考慮車貨匹配度外,還充分考慮貨物間的匹配度,基于供需信息消除貨物的物理性質(zhì)、化學(xué)性質(zhì)等帶來的沖突,實(shí)現(xiàn)車貨間的高匹配率[9]。
上述數(shù)學(xué)模型雖然對影響因素進(jìn)行了量化分析,對求解條件進(jìn)行了約束,但車貨匹配涉及車主、貨主、平臺(tái)三方主體,上述模型未考慮決策過程的主觀性和模糊性、不能衡量無法用數(shù)值表示的要素、簡單模型無法正確反映真實(shí)情況等問題。故部分學(xué)者采取群決策的方法,從雙邊匹配理論出發(fā)考慮車主和貨主的滿意度進(jìn)行車貨匹配評(píng)價(jià),引入模糊數(shù)量化語言評(píng)價(jià)的主觀性和模糊性。樂琦等學(xué)者以實(shí)現(xiàn)車貨雙方主體最高滿意度為目標(biāo),運(yùn)用線性加權(quán)法和三角模糊數(shù)重心法,構(gòu)建了多目標(biāo)雙邊匹配模型[10]。張笛等學(xué)者在考慮匹配主體的后悔規(guī)避心理行為和匹配意愿后,建立了直覺模糊偏好信息的雙邊匹配模型[11]。但三角模糊數(shù)會(huì)因參數(shù)選擇的不同引起不確定性,也無法處理多維度的模糊性。直覺模糊數(shù)應(yīng)用條件較為苛刻,應(yīng)用范圍較窄,只能應(yīng)用于隸屬度與非隸屬度之和小于1的決策情形,而個(gè)人認(rèn)知、經(jīng)驗(yàn)、對屬性理解程度的不同會(huì)使隸屬度和非隸屬度之和大于1。故本文將采用Pythagorean模糊數(shù),克服三角模糊數(shù)和直覺模糊數(shù)的不足。Pythagorean模糊集的隸屬度和非隸屬度之和大于1;比三角模糊數(shù)、直覺模糊集表達(dá)的模糊現(xiàn)象范圍更廣;描述沖突信息、刻畫并表達(dá)模糊信息的能力更強(qiáng);不僅可以精確地描述專家評(píng)價(jià)偏好,而且可以處理更加復(fù)雜的多屬性問題。自耶格爾(Yager)等提出Pythagorean模糊集以來[12],專家學(xué)者不斷地對Pythagorean模糊集進(jìn)行改進(jìn)和應(yīng)用。祝玉婷等學(xué)者考慮了評(píng)價(jià)的不確定性、不一致性和復(fù)雜性,對Pythagorean模糊集進(jìn)行改進(jìn)并將其用于可持續(xù)實(shí)驗(yàn)室的評(píng)價(jià),實(shí)現(xiàn)了對環(huán)境的保護(hù)[13]。比比哈斯(Bibhas)等學(xué)者利用Pythagorean模糊集處理不確定和不完整的信息,利用Pythagorean梯形模糊數(shù)定義的語言評(píng)價(jià)變量,最終實(shí)現(xiàn)對可持續(xù)供應(yīng)商的標(biāo)準(zhǔn)值進(jìn)行評(píng)價(jià)[14]。努爾薩(Nursah)等學(xué)者引入的分解Pythagorean模糊集,從功能和功能失調(diào)的角度對決策者的想法和看法進(jìn)行處理,對不確定信息進(jìn)行更現(xiàn)實(shí)和詳細(xì)的建模,解決了物聯(lián)網(wǎng)的可持續(xù)供應(yīng)鏈系統(tǒng)策略的選擇問題[15]。
三、車貨匹配理論與方法
(一)車貨匹配準(zhǔn)則
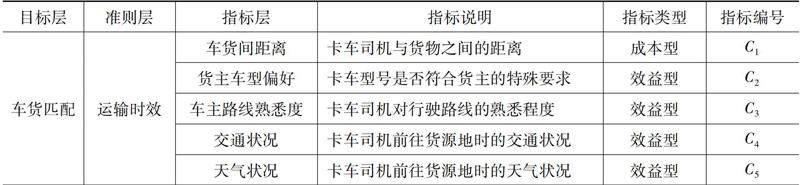
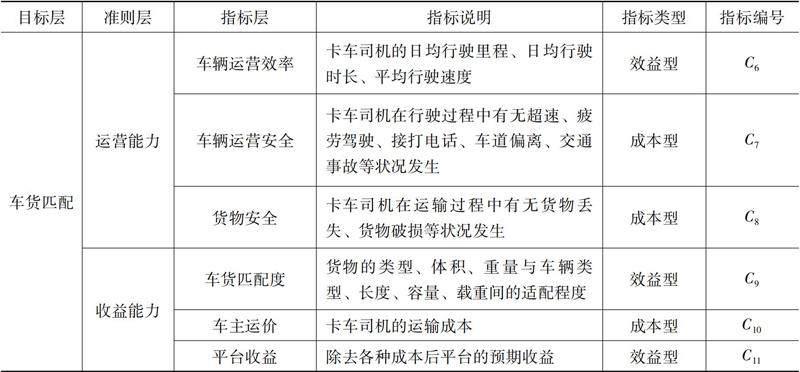
車貨匹配是雙邊匹配的研究領(lǐng)域之一,其核心是尋找一種合適的決策方法來得到最優(yōu)的車貨匹配方案,滿足匹配主體雙方需求的同時(shí)也為平臺(tái)帶來更高的效益。因此評(píng)價(jià)指標(biāo)的選取對于車主、貨主、平臺(tái)來說至關(guān)重要,平臺(tái)只有充分考慮車主和貨主的需求,在努力達(dá)到較高的車貨匹配度的基礎(chǔ)上考慮自身利益,才能達(dá)到有效匹配和三方利益最優(yōu)。為此本文從車主、貨主、平臺(tái)三個(gè)角度選取評(píng)價(jià)指標(biāo),針對行業(yè)運(yùn)價(jià)的價(jià)格戰(zhàn)問題,在穩(wěn)定運(yùn)輸成本(即車主運(yùn)價(jià))和平臺(tái)收益的基礎(chǔ)上,納入車貨匹配度指標(biāo),減少運(yùn)力的浪費(fèi),增強(qiáng)平臺(tái)的收益能力,避免平臺(tái)間的價(jià)格戰(zhàn);針對卡車司機(jī)充值平臺(tái)會(huì)員的不正當(dāng)競爭問題,在保證貨物安全的基礎(chǔ)上,納入車輛運(yùn)營效率、車輛運(yùn)營安全指標(biāo),平臺(tái)將司機(jī)的運(yùn)營能力作為匹配的重要依據(jù)之一,避免卡車司機(jī)間的惡性競爭;針對平臺(tái)算法分單不合理問題,在滿足貨主車型偏好的同時(shí),納入車貨間距離、車主路線熟悉度、交通狀況、天氣狀況指標(biāo),提升運(yùn)輸時(shí)效和訂單的成交率。同時(shí),本文將以上評(píng)價(jià)指標(biāo)分為成本型和效益型兩類(其中成本型指標(biāo)是指決策屬性越劣越好,效益型指標(biāo)是指決策屬性越優(yōu)越好),如表1所示。
表1 車貨匹配評(píng)價(jià)指標(biāo)


(二)Pythagorean模糊集


四、案例與比較分析
(一)FU網(wǎng)絡(luò)貨運(yùn)平臺(tái)簡介
FU是一家網(wǎng)絡(luò)貨運(yùn)平臺(tái),致力于在提高車輛運(yùn)行效率的同時(shí),降低貨主和車主的信息獲取成本、提升貨主和車主的運(yùn)輸服務(wù)體驗(yàn)。自成立以來FU已實(shí)現(xiàn)全國化布局,累計(jì)獲得了來自中銀集團(tuán)投資有限公司、經(jīng)緯中國、普洛斯等投資機(jī)構(gòu)的7輪股權(quán)融資;擁有超150萬名卡車司機(jī),服務(wù)覆蓋國內(nèi)31個(gè)省、直轄市、自治區(qū)(除港澳臺(tái)),337個(gè)城市;已同京東物流、順豐速運(yùn)、加多寶等多家大型企業(yè)達(dá)成業(yè)務(wù)合作,中小企業(yè)客戶也已超1萬家。FU根據(jù)歷史交易價(jià)格、車型、線路、貨物品類、天氣等因素對運(yùn)價(jià)進(jìn)行調(diào)整;根據(jù)貨品分類、交易偏好、線路偏好、車型偏好、履約能力、裝卸貨要求、運(yùn)行時(shí)效等實(shí)現(xiàn)貨源與運(yùn)力之間的精準(zhǔn)匹配。目前FU的貨運(yùn)準(zhǔn)時(shí)率高達(dá)95.2%,車輛空駛率由行業(yè)平均值45%降至6.6%,并100%實(shí)現(xiàn)了運(yùn)單的線上化和數(shù)字化。
(二)車貨信息
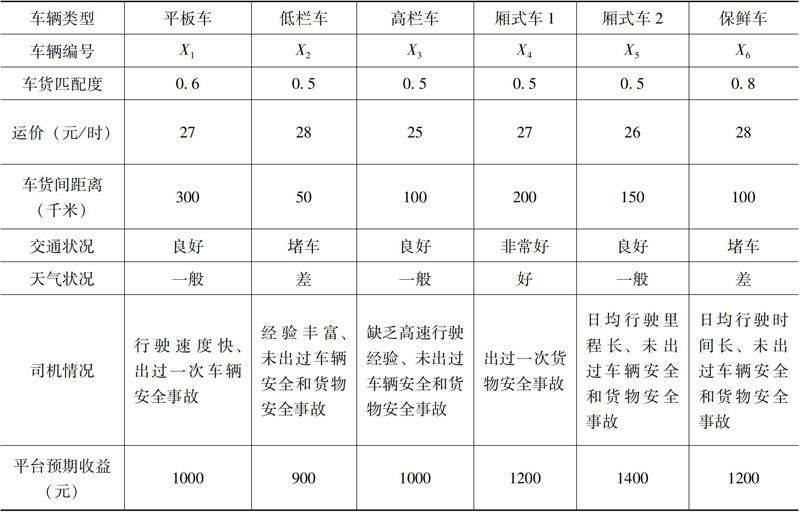
FU在某一時(shí)段接到一個(gè)運(yùn)輸新鮮水果和蔬菜且比較緊急的跨省訂單,出于時(shí)間的考慮貨主希望全程高速送達(dá)貨物。在貨主要求的時(shí)間內(nèi)該平臺(tái)有6輛車可以接受此任務(wù),6輛車的信息如表2所示。
表2 車輛信息
(三)數(shù)據(jù)計(jì)算
1.?構(gòu)造決策矩陣
針對車貨匹配決策問題,F(xiàn)U組建了一支專業(yè)隊(duì)伍,通過統(tǒng)計(jì)與調(diào)查,邀請3名行業(yè)專家對上述的6種車輛根據(jù)表1的11個(gè)指標(biāo)進(jìn)行評(píng)估,3名專家的評(píng)價(jià)語言變量如表3所示,評(píng)價(jià)結(jié)果如表4所示。
表3 專家評(píng)價(jià)語言變量與對應(yīng)Pythagorean模糊數(shù)

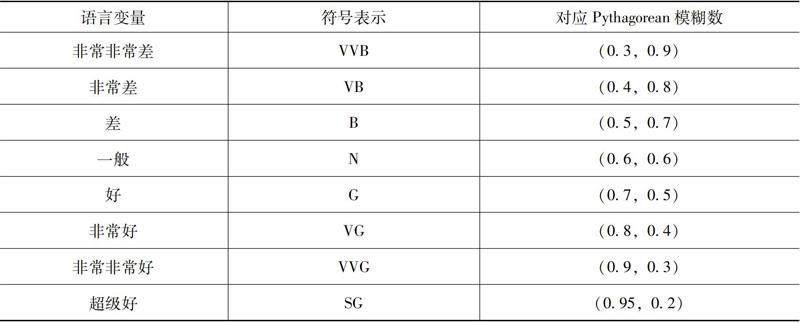
表4 專家評(píng)價(jià)結(jié)果
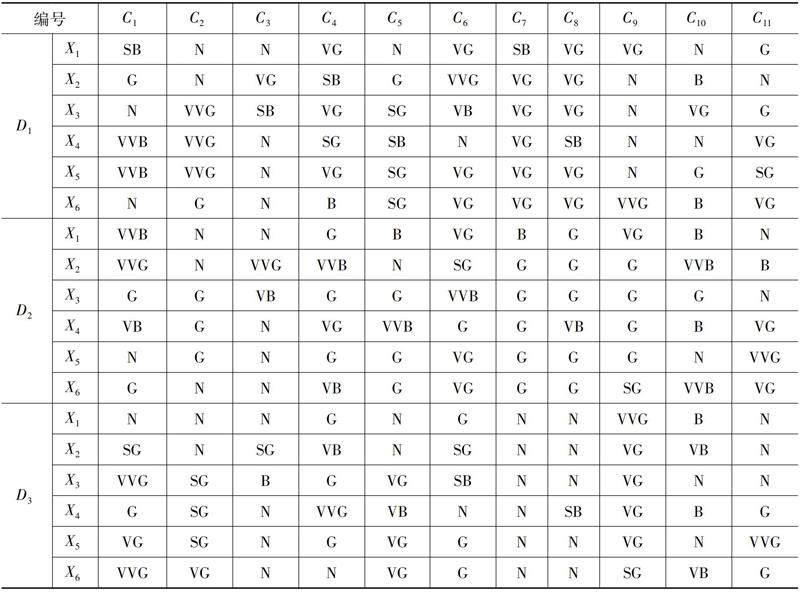
參照表3將表4的語言變量型評(píng)價(jià)信息轉(zhuǎn)化為Pythagorean模糊數(shù)型評(píng)價(jià)信息,并進(jìn)行標(biāo)準(zhǔn)化后得到?jīng)Q策矩陣Ri(i=1,2,3),如表5至表7所示。
表5 專家D1給出的決策矩陣R1
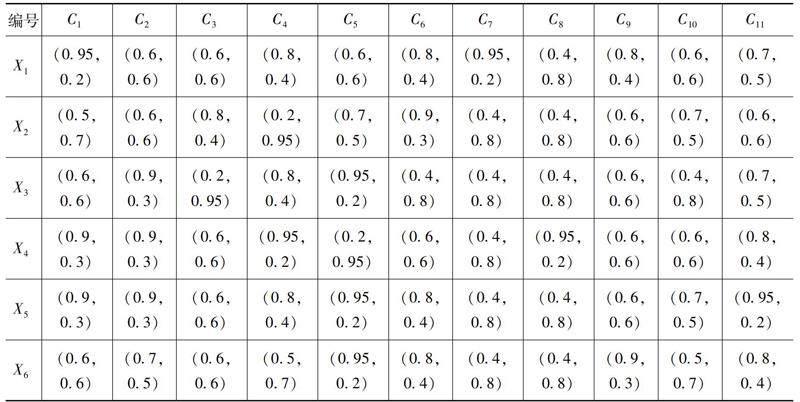
表6 專家D2給出的決策矩陣R2
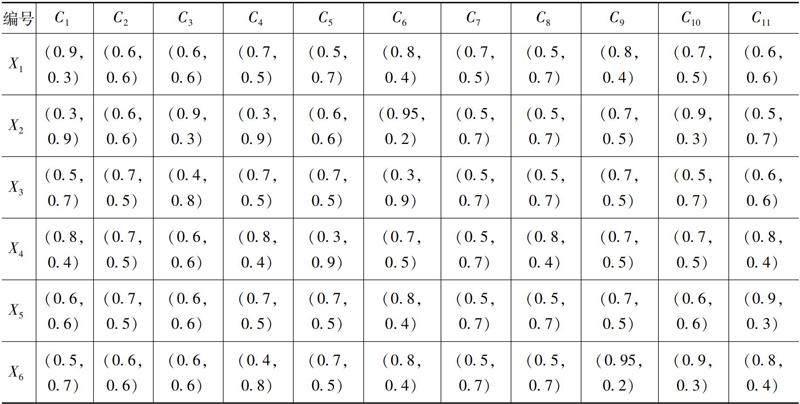
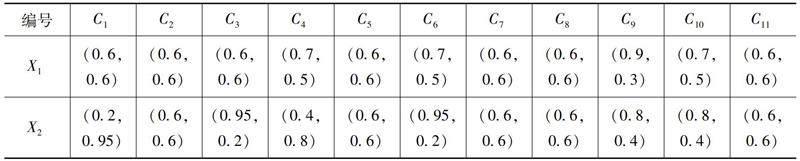
表7 專家D3給出的決策矩陣R3
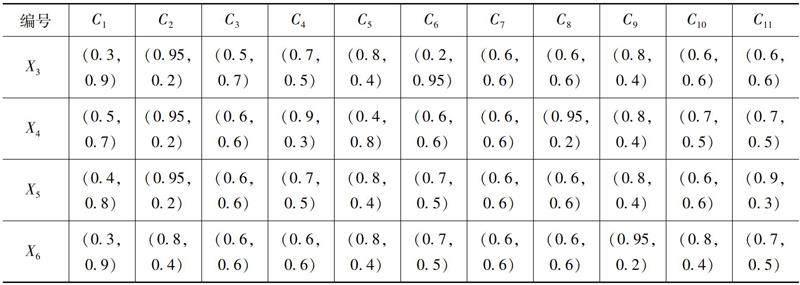
2.?計(jì)算指標(biāo)權(quán)重

根據(jù)式(6)計(jì)算出綜合評(píng)價(jià)矩陣R,如表8所示。
表8 綜合評(píng)價(jià)矩陣R

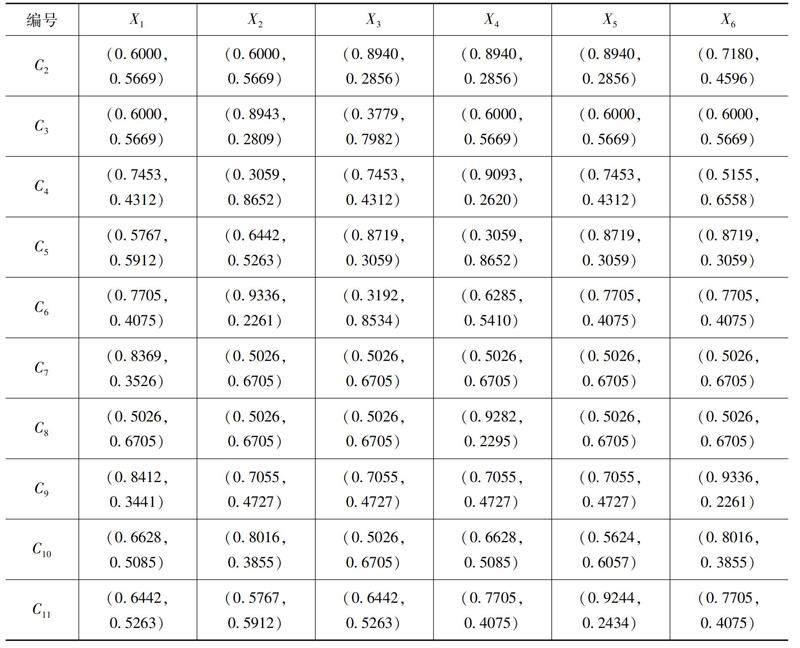
5.?計(jì)算備選方案順序
根據(jù)式(7)計(jì)算出邊界近似域矩陣Gk如下。
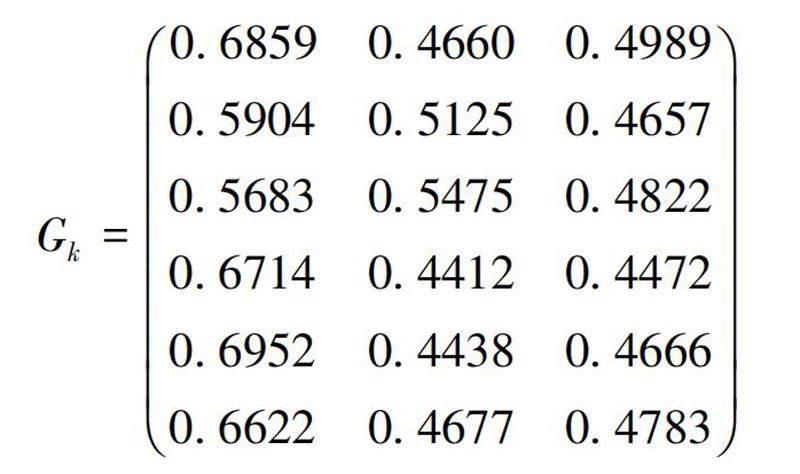
根據(jù)式(1)和式(8)計(jì)算出每個(gè)指標(biāo)到邊界近似域的距離Qkj,如表9所示。
表9 每個(gè)指標(biāo)到邊界近似域的距離Qkj

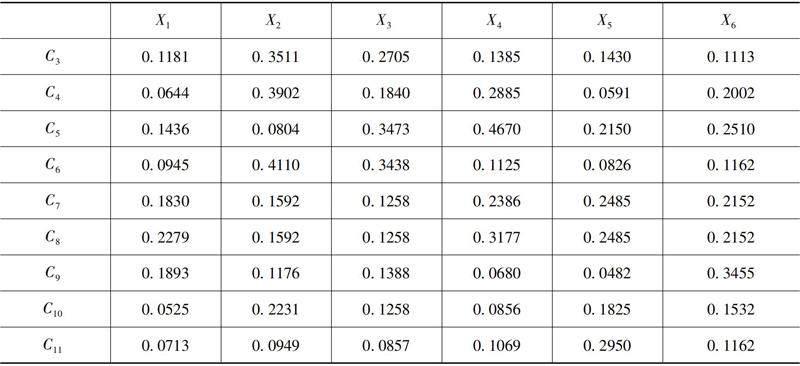
根據(jù)式(9)計(jì)算出每一個(gè)備選方案到邊界近似域的距離Dk為:D1= 1.5051,D2= 2.3822,D3= 2.2666, D4= 2.2154, D5= 1.8197,D6= 2.0174。
因?yàn)镈1
為了驗(yàn)證本文提出的方法的合理性和準(zhǔn)確性,從模糊數(shù)、屬性權(quán)重、算子、排序方法四方面進(jìn)行方法比較。在進(jìn)行比較時(shí),遵循除比較部分外,其余部分的方法與本文保持一致的原則。在查閱文獻(xiàn)后,選擇以下文獻(xiàn)進(jìn)行比較分析,通過比較結(jié)果增強(qiáng)本文方法的說服力。阿塔納索夫(Atanassov)率先提出的直覺模糊集[16],至今還有許多學(xué)者在運(yùn)用。徐選華等學(xué)者將直覺模糊數(shù)用于大群體應(yīng)急決策中,通過構(gòu)建大群體應(yīng)急決策共識(shí)模型提高群體共識(shí)水平[17];李鵬宇等學(xué)者將直覺模糊數(shù)用于最優(yōu)直播帶貨窗口的選擇中,通過改進(jìn)算子和賦權(quán)方法提高商家決策效率[18];孟凡永等學(xué)者基于前景理論將直覺模糊用于無廢城市建設(shè),提高動(dòng)態(tài)多屬性群決策的效率[19]。李娜等學(xué)者提出了用于計(jì)算屬性權(quán)重的Pythagorean模糊熵,構(gòu)建了規(guī)避后悔行為與失望行為的決策方法,規(guī)避了決策過程中的風(fēng)險(xiǎn)[20]。杜玉琴在k=1時(shí),將Pythagorean模糊哈馬赫爾(Hamacher)加權(quán)平均算子(PFHWA)轉(zhuǎn)化為Pythagorean模糊加權(quán)平均算子(PFWA),并驗(yàn)證了該方法的可行性和實(shí)用性[21]。袁汝華等學(xué)者將Pythagorean模糊數(shù)和TOPSIS法(逼近理想解排序法)相結(jié)合對長三角25座城市水資源承載力進(jìn)行綜合評(píng)價(jià)[22]。
為了減少誤差,在比較過程中用表10的評(píng)價(jià)語言集代替表3的評(píng)價(jià)語言集,實(shí)現(xiàn)從Pythagorean模糊數(shù)到直覺模糊數(shù)的轉(zhuǎn)換,且πA(x)=1-μA(x)-vA(x)。基于相關(guān)決策數(shù)據(jù),對本文的方法與四種不同方法進(jìn)行比較,備選方案排序結(jié)果如表11所示,備選方案的排序結(jié)果比較如圖1所示。
表10 專家評(píng)價(jià)語言變量與對應(yīng)直覺模糊數(shù)

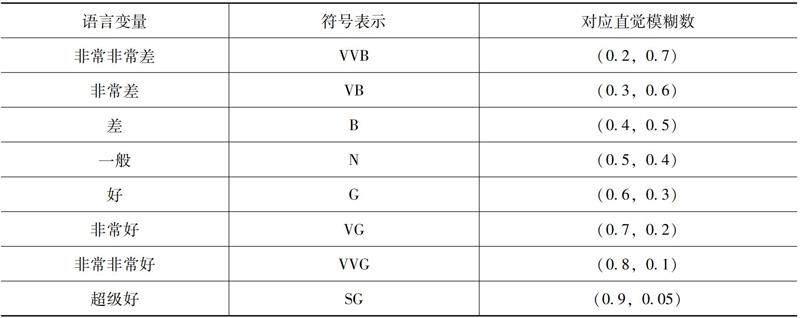
表11 不同方法下備選方案排序結(jié)果

本文的方法與三位學(xué)者提出的方法對最優(yōu)備選方案的選擇是一致的,與兩位學(xué)者提出的方法在備選方案排序結(jié)果上一致的,這印證了本文的方法的準(zhǔn)確性和合理性。本文方法對備選方案的排序結(jié)果與直覺模糊環(huán)境下的排序結(jié)果有微小的差異,與TOPSIS排序方法下的排序結(jié)果有較大差異。在不同的模糊環(huán)境下,雖然最優(yōu)備選方案的選擇是一樣的,但是本文的Pythagorean模糊數(shù)比直覺模糊數(shù)具有更強(qiáng)的描述能力和更廣的適用范圍;在不同的排序方法下,備選方案排序結(jié)果出現(xiàn)較大差異的原因可能是袁汝華教授等在運(yùn)用TOPSIS法進(jìn)行排序時(shí)再次考慮了指標(biāo)權(quán)重。不同方法下備選方案排序結(jié)果比較如圖1所示,進(jìn)一步體現(xiàn)了這種差異。
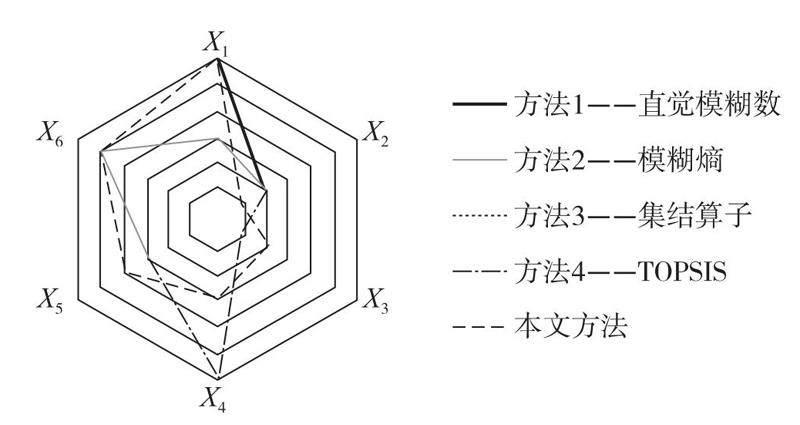
圖1 不同方法下備選方案排序結(jié)果比較
五、研究結(jié)論
針對網(wǎng)絡(luò)貨運(yùn)平臺(tái)車貨匹配過程中存在平臺(tái)間的價(jià)格戰(zhàn)、卡車司機(jī)間的搶單、平臺(tái)推薦匹配方案不合理等問題,以及國內(nèi)外主流研究方法的不足,本文對網(wǎng)絡(luò)貨運(yùn)背景下的車貨匹配問題進(jìn)行了研究。首先,在Pythagorean模糊環(huán)境下,充分考慮車主、貨主、平臺(tái)三方利益的同時(shí),建立新的車貨匹配準(zhǔn)則。其次,在車貨匹配過程中使用多屬性群決策車貨匹配方法,具體而言,采用Pythagorean模糊數(shù)確保評(píng)價(jià)信息的準(zhǔn)確性;采用反正切Pythagorean模糊熵計(jì)算指標(biāo)權(quán)重和專家權(quán)重,使指標(biāo)權(quán)重和專家權(quán)重更加客觀;采用Pythagorean模糊愛因斯坦加權(quán)平均算子把專家權(quán)重考慮在內(nèi),使綜合評(píng)價(jià)結(jié)果更加合理;采用MABAC方法進(jìn)行擇優(yōu)排序時(shí)把猶豫度納入考慮,使決策方法變得更加可靠。再次,通過FU網(wǎng)絡(luò)貨運(yùn)平臺(tái)的案例,驗(yàn)證了本文方法的可操作性與可行性。最后,從模糊數(shù)、指標(biāo)權(quán)重、算子、排序方法四方面與其他方法進(jìn)行比較,發(fā)現(xiàn)本文方法與大部分方法在備選方案的選擇及所有備選方案的排序結(jié)果基本是一致的,證明了本文方法的合理性和準(zhǔn)確性。
參考文獻(xiàn):
[1]牟向偉, 陳燕, 高書娟, 等.?基于改進(jìn)量子進(jìn)化算法的車貨供需匹配方法研究[J]. 中國管理科學(xué),2016,24(12):166-176.
[2]余海燕, 逯楠, 李小甫.?同城貨運(yùn)眾包平臺(tái)的車貨匹配模式對比研究[J]. 運(yùn)籌與管理,2022,31(11):206-212.
[3]TIAN R, WANG C, MA Z Y, et al.?Research on vehicle-cargo matching algorithm based on improved dynamic Bayesian network [J]. Computers and industrial engineering, 2022,168: 108039.
[4]李建斌, 周泰, 徐禮平, 等.?貨運(yùn)O2O平臺(tái)有時(shí)間窗同城零擔(dān)集貨匹配優(yōu)化決策[J]. 系統(tǒng)工程理論與實(shí)踐,2020,40(4):978-988.
[5]WANG H F, HUANG M, KUANG H B.?One-to-one stable vehicle cargo matching in the fourth party logistics [J]. Chinese control and decision conference,2021, 4221-4226.
[6]JIANG C B, XU J M, LI S F, et al.?The order allocation problem and the algorithm of network freight platform under the constraint of carbon tax policy [J]. International Journal of environmental research and public health, 2022, 19: 1-27.
[7]朱江洪, 王睿, 李延來.?基于不確定語言關(guān)聯(lián)性信息的車貨雙邊匹配決策方法[J]. 系統(tǒng)科學(xué)學(xué)報(bào),2018,26(1):86-91.
[8]ZHANG Q Y.?Vehicle-cargo matching optimization model for vehicle capacity scheduling platform [J].International conference on advances in management science and engineering,2020, 260-267.
[9]張青杰, 竇永香, 陳姝.?公路貨運(yùn)供需信息的組合匹配模型[J]. 統(tǒng)計(jì)與決策,2018,34(14):72-75.
[10]樂琦, 朱加貴.?基于三角直覺模糊數(shù)信息的雙邊匹配決策[J]. 運(yùn)籌與管理,2021,30(1):57-62.
[11]張笛, 戴紅軍, 劉曉瑞.?考慮后悔規(guī)避與匹配意愿的直覺模糊雙邊匹配方法[J]. 運(yùn)籌與管理,2020,29(10):132-139.
[12]YAGER R R, ABBASOV A M.?Pythagorean membership grades, complex numbers, and decision making [J]. International journal of intelligent systems, 2013, 28 (5): 436-452.
[13]祝玉婷, 韓瑩, 袁安富.?基于改進(jìn)的Pythagorean模糊語言集的可持續(xù)實(shí)驗(yàn)室評(píng)價(jià)方法[J]. 運(yùn)籌與管理,2019,28(11):149-155.
[14]BIBHAS C G, MAHATAB U M, PRANAB B.?Pythagorean fuzzy dematel method for supplier selection in sustainable supply chain management [J]. Expert systems with applications, 2022, (193): 116396.
[15]NURSAH A, CENGIZ K.?CODAS extension using novel decomposed pythagorean fuzzy sets: strategy selection for IOT based sustainable supply chain system [J]. Expert systems with applications, 2023, (237): 12153.
[16]ATANASSOV K.?Intuitionistic fuzzy sets [J]. Fuzzy sets and systems, 1986, 20(1): 87-96.
[17]徐選華, 肖婷, 陳曉紅.?社會(huì)網(wǎng)絡(luò)環(huán)境下基于群智知識(shí)融合的大群體應(yīng)急決策共識(shí)模型[J]. 中國管理學(xué),2021,1-14.
[18]李鵬宇, 吳沖, 張之云.?基于直覺模糊語言集的直播帶貨窗口選擇方法[J]. 運(yùn)籌與管理,2023,32(6):119-125.
[19]孟凡永, 蔣蕾.?交互動(dòng)態(tài)直覺模糊前景理論VIKOR法及在無廢城市建設(shè)中應(yīng)用[J]. 運(yùn)籌與管理,2023,32(4):47-52.
[20]李娜,高雷阜,王磊.基于Pythagorean模糊熵的風(fēng)險(xiǎn)型決策方法——考慮后悔與失望規(guī)避[J].運(yùn)籌與管理,2020,29(6):130-138.
[21]杜玉琴.?Pythagorean模糊Hamacher算子及其應(yīng)用分析[J]. 運(yùn)籌與管理,2021,30(7):218-222.
[22]袁汝華, 王霄漢.?基于Pythagoras-TOPSIS法的長三角水資源承載力綜合評(píng)價(jià)分析[J]. 科技管理研究,2020,40(15):71-79.
Research on Vehicle-cargo Matching of Network Freight Platform
Based on MABAC Method in Pythagorean Fuzzy Environment
LIU Ling1, WU Rui-dong1, MA Nan2, XIA Lu1
(1.School of Logistics and Management Engineering, Yunnan University of Finance and Economics,
Kunming, Yunnan 650221;
2.Dehong Prefecture Company, Yunnan Tobacco Company,Mangshi, Yunnan 678400)
Abstract:
In consideratun of the problems of price war among platforms, order grabbing among truck drivers and unreasonable platform recommendation matching scheme in the process of vehicle and cargo matching on network freight platform, the MABAC (Multi-Attribute Border Approximation Area Comparison)decision-making method is adopted to match vehicles and cargo under Pythagorean fuzzy environment, and the special requirements of shippers are considared.?Firstly, the evaluation index system of vehicle and cargo matching was established under the premise of considering the interests of truck drivers, shippers and platforms.?Secondly, Pythagorean fuzzy number was used to represent expert evaluation language, and arctangent entropy on Pythagorean fuzzy sets was used to calculate index weight and expert weight.?Finally, the alternatives were sorted according to MABAC method.
Keywords: vehicle and cargo matching; Pythagorean fuzzy; arctangent entropy on Pythagorean fuzzy sets; MABAC
基金項(xiàng)目:2018年國家自然科學(xué)基金地區(qū)科學(xué)基金項(xiàng)目“基于時(shí)間成本優(yōu)化的面向訂單制造企業(yè)生產(chǎn)與運(yùn)輸協(xié)同調(diào)度問題模型與算法研究”(71862034);2023年國家自然科學(xué)基金面上基金項(xiàng)目“云服務(wù)驅(qū)動(dòng)的供應(yīng)鏈平臺(tái)治理機(jī)制形成及價(jià)值創(chuàng)造機(jī)理研究”(72372143);2023年云南省煙草公司德宏州煙草公司科技計(jì)劃項(xiàng)目“綠色低碳卷煙分揀裝箱及配送策略應(yīng)用研究”(DHYCKJ202302)

