極限思維助力物理習題教學創新策略分析

張巖

【摘要】本文從核心素養的角度出發，深入探討物理習題教學中極限思維的應用及其對教學質量提升的影響.通過運用極限思維，可有效突破傳統物理習題教學模式的局限性，使學生在面對復雜問題時能夠超越既定的解題框架，洞察問題本質，并創造性地尋找解決方案.通過實例分析，進一步驗證極限思維在增強學生創新思維、提高解題效率與準確性方面的積極作用，并在此基礎上提出一系列具有針對性的教學創新策略.旨在幫助學生更好地掌握物理習題的解題技巧，提升學生的物理學科素養.

【關鍵詞】極限思維；高中物理；習題教學

《關于全面深化課程改革落實立德樹人根本任務的意見》中明確提出，“核心素養是黨教育方針的具體體現，是連接宏觀教育理念、培養目標與具體教育教學實踐的關鍵橋梁”.因此，培養學生的核心素養已被視為重要的教育目標之一.在物理教育中，習題教學是培養綜合素養和解決問題能力的關鍵環節.然而，傳統的物理習題教學往往過分注重計算和記憶，而忽視了學生的思維能力和創新精神的培養.所以，在核心素養的視角下，對物理習題教學的創新策略進行研究和實踐，對于提升物理教育的質量和效果具有重要意義.

1 基于極限思維，尋找解題突破口

極限思維的運用，實質上是激發學生的創新思維，引導學生在遇到復雜問題時，勇于擺脫既定思維框架的束縛，努力挖掘問題背后更深層次的基本原理和最大潛在可能性.在解題過程中，極限思維要求學生將問題置于極端條件下進行深思，從而激發創新思維，找到解決方案.傳統思維方式雖然鼓勵學生拓寬問題的視野，從多角度審視問題，但經常忽視在問題推至極端狀態下可能存在的突破口.而極限思維則倡導學生設想極端情境，例如“如果某一變量趨于無窮大，結果會如何？”或“如果某一條件完全不存在，情況又將怎樣？”通過此類極端假設，可以挑戰并重新定義問題的邊界，進而實現解題策略的突破.

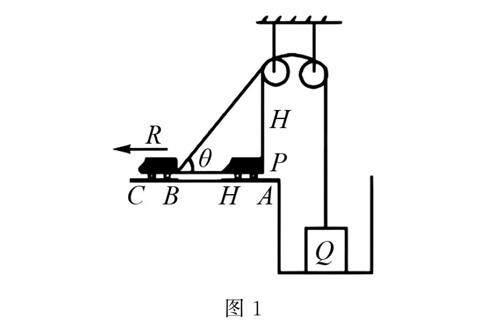
例1 現有一輛小車按照圖1所示的連接方式，想要通過設置的定滑輪來拉升落入到水井當中的一個質量為m的物體.小車的尾部與物體上方分別通過繩子的兩端P和Q連接，形成圖1所示的布局.假定滑輪位置固定，繩子長度不變，忽略滑輪和繩子間的摩擦以及滑輪繩子的重量和尺寸.起始時，小車停放于點A，同時左右繩子均處于拉緊狀態.左側繩子長度設為H.小車向左水平方向加速運動以提升物體，并最終移動至點C.小車從A至B的距離同樣為H.當小車通過B點時，測得其速度為vB.試求小車自A點行駛到B點時繩端所形成拉力對物體所做的功.

分析

高中學生在分析物理問題時常會考慮用動能定理來解決問題，特別是在需要計算繩索對Q端的拉力所做功的場景下.這類問題的關鍵在于確定物體在特定位置（如B點）的速度大小vt.然而，學生們在實際操作過程中可能會遇到像vt=vtcosθ這樣的錯誤推導.對于問題的正確分析，可以從圖1中剖析繩索拉伸速度v隨角度θ變化的關系.學生們可以被引導以B點為起點進行外推，這涉及兩個理想極限狀態的考慮：一是當θ為90°時，繩速是0；二是當θ為0°時，繩索速度和小車速度恒定并相等.當從點A進到無窮遠處時，繩索的遞增規律會呈現如下這一基本特征：v=vcos90°=0.因此，驗證小車在A點、B點以及無限遠位置處速度是否符合此基本規律，將有助于學生解決題中難點，進而快速得出正確答案.實際解題時，將物體提升過程作為研究對象，運用動能定理可以有效得出結論.

WF=mg（2－1）H=12mu2tVt=VBcos45°，

通過求解，得：WF=14mv2B+（2－1）mgH.

小結

極限思維在解決物理問題中展現了其獨特的價值，尤其是在面對動能定理難以解決復雜場景時.例如，在處理涉及繩子拉伸速度隨角度變化的問題時，使用傳統的解題思路可能會陷入困境.然而，通過引入極限思維，可以設定兩個理想狀態：一是當角度趨近于90°時，二是當角度趨近于0°時.在這兩個極限狀態下，學生能夠洞察繩索速度的基本規律，即當角度為90°時，繩索速度為0；而當角度為0°時，繩索速度等于小車的速度.這種極限分析的方法不僅幫助學生突破了解題的難點，還引導他們快速找到了正確答案.因此，通過極限思維，學生可以在復雜問題中尋找突破口，從而達到更深層次原理的理解和問題解決方案的創新.

2 基于極限思維，提升解題速度

在高中物理教學與問題解決過程中，頻繁涉及將特定的物理量局限于特定的域內.在這類情境下，極限思維法則顯得尤為關鍵，其允許解題者通過設定物理變量到它們的極限（或臨界）情況來進行問題的解答.具體地，可以假設這些變量達到它們的邊界狀態，并以此狀態為基準來邏輯推導整個問題，從而得出更加嚴密與合理的結論.

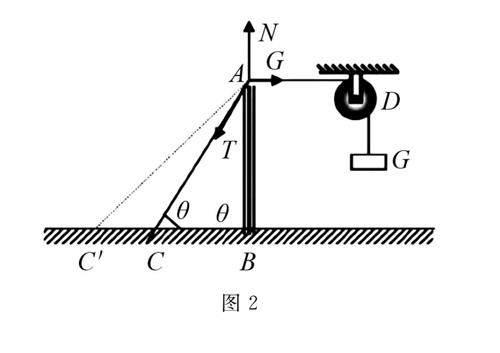
例2 圖2中整個裝置處于平衡的狀態，如果將細繩AC換成一個更長的AC′，而桿AB依然保持豎直．AC換成AC′以后，該裝置依然可以保持平衡，那么AC′繩子所受的張力T與AB桿所受的壓力N較之前有什么樣的改變？

分析

在分析這類問題時，許多學生會遵循傳統的解題路徑，即先假設AC與水平線之間的角度，然后根據力的合成與分解原理構建方程進行求解.雖然這種方法邏輯上沒有問題，但其操作過程復雜且易出錯.為了簡化解題過程并減少出現錯誤的可能性，教師可以引導學生采用極限思維來巧解這類難題.具體來說，可以設想AC與水平方向的夾角逐漸趨近于0°，此時水平支持力N逐漸消失，只剩下拉力T等于重力G.反之，當夾角增加至90°時，支持力N將達到最大值，此時拉力T大小等于支持力N.根據題目設定，當AC變為AC′時，其與水平方向的夾角減小，由此可以推斷出這種變化將導致拉力T和支持力N同比例減小.通過比較這兩種情況，能夠有效地推斷出力的變化趨勢，從而顯著簡化解題步驟.

小結

在物理解題中，引入極限思維可以提升解題效率和解題速度.該方法通過考慮物理量在它們極端狀態下的行為，來邏輯推導整個問題的解.以圖2中的平衡問題為例，傳統的解法通過構建方程求解，而用極限思維則考慮：當AC與水平線夾角趨近0°時，支持力N消失，拉力T等于重力G；夾角為90°時，N最大，T等于N.當AC繩變長為AC′時，夾角減小，推斷出拉力T和支持力N均減小.這種方法簡化了解題步驟，易于理解和運用.

3 基于極限思維，檢查結果

在處理物理學問題時，高中學生除需解決具體問題外，更應對解題結果進行詳盡的復核，以確保答案的準確性.在某些情況下，學生可能會發現采用傳統的解題策略尤為棘手.此時，教師們可引導學生運用極限思維作為一種驗證解題正確性的有效手段.

例3 將一個物體放在做勻減速運動的升降機中，其加速度a=1.2g，問整個運動中物體對于升降機底板的壓力是多少？

分析

在解決此題目時，許多學生會依據牛頓第二定律進行運算，得出ma=mg－N，從而推導出N=mg－ma=0.2mg.為了驗證這一結果的準確性，教師可以運用極限思維進行進一步分析.假設在升降機上升過程中，加速度達到臨界值a1，且a1=g，此時物體將進入失重狀態，對底板的壓力將降為0.然而，根據題目中給出的信息，物體的a=1.2g，顯然a1＜a.因此，可以斷定學生在解題過程中存在錯誤.實際上，在這種情況下，物體處于完全失重狀態，對底板的壓力應為０.

例4 已知一條輸電線路電阻為1.0Ω，輸送的電功率為100 kW.若分兩種情況對該線路進行電能輸送：一種情況下使用400伏特的電壓，另一種情況下使用10000伏特的高壓電.請分別計算在這兩種電壓條件下輸電線路的發熱損失的功率是多少？

分析

經過深入分析，學生們針對電功率的計算問題，提出了以下觀點.按照電功率計算公式 P=U2R，他們在計算線路發熱損失功率時得出了以下結論：在低壓送電情況下，損失功率P1=40021W=1.6×105W；而高壓輸電時，損失功率P2=1000021=108W.

在學生解決問題后，教師應引導學生運用極限思維來進行檢查，就會發現這種解題思路是錯誤的，假設輸電電壓趨向于無限大時，輸送功率在一定程度上增長，理論上輸電電流將逐漸趨于零.反之，若輸電電壓接近于零，為了維持一定的輸出功率，所需的輸電電流將不可避免地趨向無限大.根據焦耳定律（電流熱效應），在高壓輸電系統中，降低輸電線路的發熱量是降低功率損耗的關鍵.通過引導學生使用極限概念來綜合審視這些情況，可以強化學生對問題本質的理解，并提高他們解題的精確性，這是一種在高中物理教學中提升學生解題質量的有效方法.

4 結語

核心素養視角下的物理習題教學創新策略強調了運用極限思維來提升學生解題能力與獨立思考能力.這不僅有利于學生更深入地理解物理原理，還有助于培養他們在面對各類復雜問題時的創新能力和邏輯推理能力.通過實例分析，本文闡釋了極限思維在物理教學中的應用價值，以及它在促進學生核心素養發展方面所起到的關鍵作用.教師在設計物理習題時應結合學生的思維特點和問題解決的實際需要，引導學生運用極限思維進行探索和實踐，以達到創新教學的目的.

參考文獻：

［1］呂曉莉.核心素養視角下高中物理新教材習題特點淺析［J］.現代教學，2023（07）：53-54.

［2］汪小龍.核心素養視角下的習題復習課設計策略——以人教版“質量與密度”為例［J］.中學物理教學參考，2022，51（15）：38-40.

［3］張躍文，司福華.核心素養下高三物理復習習題課教學——例談“闖關問題法”習題教學［J］.數理天地（高中版），2022（22）：95-97.

［4］陳志慧.基于學科核心素養的高中物理習題教學設計研究［J］.數理化解題研究，2022（27）：74-76.

［5］鄺玉蘭，莫黎斌.高中物理習題教學與創新實驗結合的課堂模式探討［J］.廣西物理，2022，43（02）：237-241.