框架預應力錨桿支護結構地震永久位移計算

劉東漢

摘 要：地震永久位移是評定結構抗震性能和安全性能的關鍵因素，尤其是對框架預應力錨桿支護結構這種復雜的柔性支護結構來說更加關鍵，其數值取決于結構的材料特性、形式及地震作用的強度等因素。因此，研究支護結構在地震作用下的永久位移對提高支護結構的抗震能力具有重要作用。文章針對框架預應力錨桿支護結構地震永久位移的計算方法展開研究，探究了該結構在地震作用下的變形規律和抗震能力，提出了關于永久位移可行性計算方法。文章主要運用擬靜力法、極限分析上限法等理論計算方法，利用極限分析上限法推導得出了框架預應力錨桿支護結構地震屈服加速度，并根據該參數計算了結構的地震永久位移。通過MATLAB編程軟件理論計算公式進行計算，并與數值模擬分析結果進行對比，驗證了公式的有效性與正確性，可為支護設計提供一定的依據。

關鍵詞：框架預應力錨桿；支護結構；極限分析上限法；地震永久位移；有限元模擬

中圖分類號：TU432 文獻標志碼：A DOI：10.3969/j.issn.1672-6375.2024.5.009

0 引言

支護結構的變形特性對于支護結構的設計和施工至關重要。通過研究框架預應力錨桿支護結構的變形規律，可以為結構設計提供基礎數據，使結構能夠滿足安全穩定的要求。

朱彥鵬等[1]考慮了結構與土體的相互作用，依據施工過程，將眶鋸預應力錨桿設計工作分為開挖和工作2個階段，同時提出一種可以控制側向位移的設計方法，能夠確定施加預應力的大小，根據該方法對實際工程進行設計，得出結論：確定合理的錨桿預應力大小是不可或缺的，這對框架預應力錨桿的設計至關重要。周勇和朱彥鵬[2]認為頂部位移是重要的變形控制指標，根據梯形土壓力模型，通過力法計算支護結構的頂部靜力位移，并對施工荷載、第一排錨桿到坡頂的距離、錨桿水平間距以及豎向間距等因素對頂部位移的影響進行分析。周勇和朱彥鵬[3]考慮基坑開挖的影響，將錨桿自由段視為彈簧，將開挖階段的支護結構視為底端鉸接，基于這種假設將坡面水平的計算簡化，同時以一實際工程為例進行計算，得出了較為符合的結果，并依據幾何模型，進行了室內模型試驗，實測結果與理論計算結果在總體趨勢上較好地吻合。

當前，針對地震作用下框架預應力錨桿支護的邊坡永久位移計算研究還較少，尚需深入探索。目前的研究大多是基于振動臺的室內試驗，對于地震作用框架預應力錨桿支護邊坡永久位移計算方法的研究還略顯不足。因此，地震作用下框架預應力錨桿支護邊坡永久位移的計算方法仍然需要進一步探索。

文章針對框架預應力錨桿支護邊坡進行了研究，主要包括以下幾個方面：（1）總結框架預應力錨桿支護邊坡的基本特征和變形機理；（2）基于擬靜力法和極限分析上限法，計算地震作用下邊坡的外力做功與內能耗散，從而得出地震屈服加速度，最后通過計算得出了地震作用下框架預應力錨桿支護邊坡的永久位移；（3）基于某工程實例，將計算結果與模擬數值進行對比，驗證計算方法的可靠性和正確性，為邊坡加固工程設計提供了良好的借鑒。

1 框架預應力錨桿支護結構基本概述

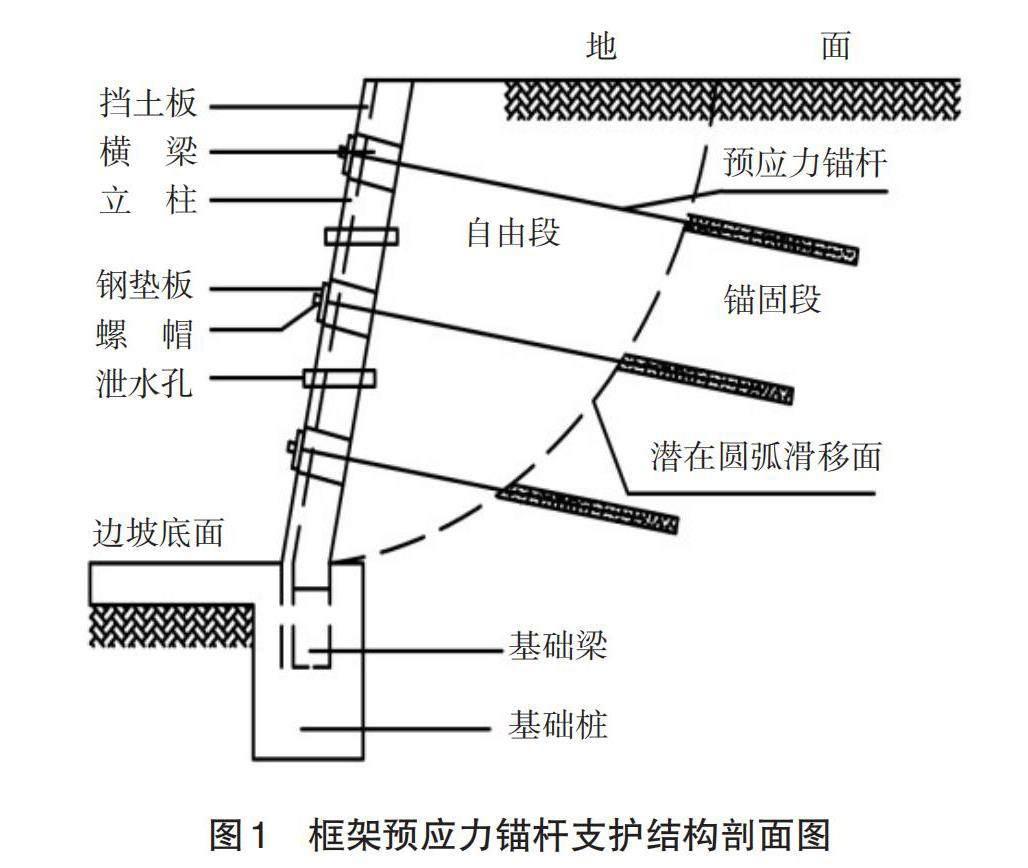
框架預應力錨桿結構作為一種新型的邊坡擋土結構，旨在提高邊坡土體力學性能[4]。該結構由擋土板、框架、錨桿及墻后土體組成，利用它們的協同作用來實現支擋作用。相較于傳統支擋結構，該結構具有更多優勢，其剖面圖如圖1所示。

在設計框架預應力錨桿支護邊坡時，需要考慮多個因素，包括挖掘場地的類型、邊坡支護結構類型、支護結構類型，以及施工條件等[5]。支護結構可采用高強度鋼材或混凝土材料制成。這些設計措施的目的是提高邊坡支護結構的穩定性和安全性，以確保其能夠有效地抵御挖掘過程中的土壓力，并為工程建設提供可靠的支撐保障。

2 極限分析上限法

20世紀50年代，Drucker等提出了與屈服條件有關的流動法則，基于速度場與靜力場的結合，建立了極值理論并證明了極限分析上、下限定理。該定理因其簡便、適用性強，深受廣大學者們的喜愛。極限分析法最大的特點和優點是對研究對象的幾何形狀沒有要求，無論是怎樣的不規則模型，模型上的荷載如何復雜，運用極限分析定理都可以求得一個與實際狀況較為相符的計算結果。除此之外，該方法在實際工程應用中也較為簡單，可將工程中的破壞模式以幾何圖形的形式表達。經過諸多學者對極限分析法的改進、研究及實際工程中的應用，認為該方法比較可靠，可以運用于實際工程[6]。

在極限分析理論中，通常會忽略材料的應力-應變圖中的應變軟化過程（圖2），但在實際工程中，絕大部分土體的應力-應變圖在到達最大值后，會隨著應變的增加而進入軟化階段，最終出現殘余應力的表現。因此，極限分析定理中所假設的理想剛塑性材料是指應力達到屈服后，隨著應變的不斷增加，應力不發生變化。雖然理想剛塑體材料是一種理想狀態，但是在巖土問題中，該假設所得到的結果比其他假設的結果更加合理。

材料進入塑性階段后，其應力-應變關系不再是一一對應，而材料的屈服準則則是判斷其由彈性階段進入塑性階段的依據。經過試驗研究得出不同應力路徑下材料的應力-應變關系，將屈服點連接形成空間曲面，即材料的彈塑性分界面。常見的屈服準則有Mohr-Coulomb、Von Mises、Tresca等，巖土工程中常用Mohr-Coulomb屈服準則。當材料發生塑性流動時，其屈服函數可以用一個表達式來描述：

在Mohr-Coulomb屈服準則中，塑性流動在土體的任意處都可發生，此時，應該滿足以下條件：τ=c+σtanφ （2）

土體的剪切應力值與正應力σ及土體的黏聚力c呈線性關系，式中c、φ為常數，φ為土體內摩擦角。

將式（2）改寫為主應力的形式：

確定塑性變形的應變增量方向是流動法則在塑性增量理論中的重要內容，而與應力增量方向不同是材料發生塑性變形的一般情況。因此，在塑性增量理論中，流動法則的研究非常關鍵。

流動法則是指材料在一定的應力狀態下發生塑性應變時，材料應力的大小和方向的一般規律和規定，流動法則的確定是建立在材料的本構關系和塑性行為規律的基礎上。材料的本構關系是指在一定的應力狀態下，應變之間的關系，有線性關系和非線性關系兩種。

1928年，Mises提出了彈性勢的概念，Mises認為，塑性流動狀態也有與彈性勢類似的函數，就是塑性勢。其函數表達式為：

材料在屈服后進入塑性流動狀態，應力不變，而應變則會無限增大。在塑性流動狀態中，材料的應變可以間接地由塑性勢函數表達，通過塑性應變增量的大小和方向來確定。此時，塑性勢函數可以用來表示塑性應變增量的大小函數：

式中：dλ為非負的塑性乘子。

通過公式（5）可以確定塑性應變增量的方向。若屈服面F與塑性勢能面Q重合，由F=Q所得到的關系稱之為加載條件相關聯的流動法則。相關聯流動法則的函數關系如下可知：

根據土體的本構關系，塑性極限分析上限法可以直接計算出土體極限狀態下的荷載和速度，而忽略了材料應變軟化過程。假設在任意可行的速度場中，應變場率和速度場內外力做功與內能耗散相等，可以確定荷載，其值一定大于或等于實際的極限荷載。這個定理稱為極限分析上限定理，可以使用虛功方程表達：

3 地震荷載作用下邊坡地震永久位移擬靜力計算

3.1 計算假定

在研究預應力錨桿邊坡地震位移時，采用極限分析上限法，將地震荷載的加速度系數均勻分布于墻高，并將其視為慣性力進行考慮。在計算過程中，需要結合相關研究材料和結果，并滿足以下假定：

（1）研究土體符合相關的流動法則；

（2）假設預應力錨桿邊坡的滑移面為對數螺旋線滑移面，并且最危險滑移面通過墻底；

（3）墻后填土均勻，在邊坡破壞時錨桿達到極限值；

（4）滿足平面應變假設。

3.2 計算模型分析

將整個滑動楔體ABC看作繞著旋轉中心O點轉動的旋轉體，旋轉角速度為Ω，邊坡高度為H，h f 為錨桿高度。假設邊坡的土體容重為γ，內摩擦角為φ，土體黏聚力為c，地震水平加速度系數為k h ，豎向地震加速度為k v ，采用塑性力學上限法分析墻土的動力特性，為了計算簡便，將OB、OA的傾角分別假定為θ B 和θ A ，依據圖3的計算模型可以得出對數螺旋滑移面的方程為：

式中： r A 為對數螺旋滑移面上與水平方向夾角為 θ A 時的極徑，即OB的長度為

由此可以得出OB的長度為：

根據邊坡模型的幾何關系可以得出L（AC段長度）和H的表達式為：

式中：β為邊坡傾角。

3.3 重力作用下邊坡外功計算

3.3.1 邊坡OAB部分求解

對OAB部分土體取一微元體進行分析計算，由圖4可得OAB區域土體重力所作的外功率。

由圖4可得到微元體OAB所作功率為：

將dw 1 沿著OAB區域進行積分計算，即可得到OAB土體所做外功率w 1 ：

其中：

將式（13）代入式（12）中可得：

由此可得，式（14）為OAB區域內土體自重所作的功率。

3.3.2 邊坡OAC部分求解

對OAC部分土體進行分析計算，由計算簡圖可得OBC區域土體重力所作的外功，如圖5所示。

同理，即可得到OAC部分土體所作功率為：

由此可得，式（15）為OAC區域內土體自重所作的功率。

3.3.3 邊坡OBC部分求解

對 OBC 部分土體進行分析計算，由圖 6 可得OBC區域土體重力所作的外功率。

同理可得到微元體OBC所作功率為：

至此，已經求得重力所做功的計算式，由疊加法可得土體ABC所作功的大小為：

3.3.4 地震荷載做功

基于地震的復雜性，目前學者們在研究地震時常常運用擬靜力法來研究地震工程問題。文章在分析地震作用時使用擬靜力法考慮地震作用。

將水平和豎直地震作用分別用k h 和k v 來表示。

式中：ξ是k v 相對于k h 的比例系數。

由圖2可知外功率做功除了重力以外還有水平地震荷載和豎向地震荷載。首先考慮豎向地震荷載，由于豎直方向的地震荷載與重力方向一致或相反，則豎向地震荷載的做功可表示為：

其中f 1 、f 2 、f 3 表達式為（13）、（16）、（18）。

對于水平地震荷載的計算可以參照上文計算方法得到：

其中土體OAB在水平地震荷載作用下所做的功 w k h -5 以及f 4 的表達式如下式：

土體 OAC 在水平地震荷載作用下所做的功w k h -5 以及f 5 的表達式如下式：

土體 OBC 在水平地震荷載作用下所做的功w k h -6以及f 6 的表達式如下式：

將式（24）、（25）、（28）代入（22）中，即可求得土體ABC在水平地震荷載作用下做的功。

3.3.5 錨索拉力做功

假設T為預應力錨桿的錨固值，錨桿與水平面的夾角為α，確定邊坡上錨桿位置的角度為θ M ，邊坡錨桿位置距坡底距離為h f ，錨桿與坡面交點為M，錨桿與對數螺旋滑移面的交點為N。M點的直角坐標系下的位置為（x M ，y M ），在極坐標系中對應的角度為θ M ，N點的直角坐標系下的位置為（x N ，y N ），在極坐標系中對應的角度為θ N 。由幾何關系可知：

基于對數螺旋線破壞面，當錨桿的拉力作用在M點時，錨桿拉力T做功的能量方程為：

基于對數螺旋線破壞面，當錨桿的拉力作用在N點時，錨桿拉力T做功的能量方程為：

由已知的研究結果可知式（32）、式（33）的計算方法是一致的，文章在計算錨桿拉力T所作的外功時，選用（32）進行計算。

3.4 地震作用下邊坡內能耗散計算

假設邊坡內部的變形一致，即塑性破壞時不產生能量損耗。邊坡土體沿著對數螺旋線面破壞產生的內能耗散是由土體黏聚力所產生的能量。在計算時對數螺旋形上取一微元體，其微分長度dl為：

因此，在整個對數螺旋滑移面上土體黏聚力c所產生的能量耗散率w c 的表達式為：

將 r（θ）=r A e（θ-θ A ）tanφ和 v（θ）=rΩ 由此可得，土體黏聚力所作內功為：

3.5 框架預應力錨桿支護結構地震屈服加速度系數

根據極限分析法，當機構處于臨界滑動狀態時，其外力做功與內能耗散相等時，支護結構處于極限平衡狀態，根據極限分析可得：

W g +W kh +W kv =W r +W t （37）

當處于極限平衡狀態時，定義水平地震系數k h為結構地震屈服加速度k s ，此時可得出支護結構破壞的不安全上限值，支護結構所對應的地震加速度為支護結構的地震屈服加速度k s ，其表達式為：

將式（22）、（24）、（25）、（31）、（36）、代入上式（38）中可得框架預應力錨桿支護結構地震屈服加速度系數：

式中：地震屈服加速系數為k s 。

框架預應力錨桿支護結構在不同的滑移面上有不同的解，為了邊坡的安全，應求得最小屈服加速度解，從而得到最危險滑移面，公式（39）中有θ A 、θ B 2個未知參數，將求解屈服加速度問題變為求解（39）的最小值問題，則有：

為了求得框架預應力錨桿支護結構邊坡處于臨界狀態時對應的地震的屈服加速度系數k s ，（40）方程應滿足如下約束條件：

因此，根據式（39）、（40）、（41）聯立后即可確定θ A 、θ B ，代入（39）中即可確定最小地震屈服加速度系數k s-min ，即在下一節中計算永久位移時框架預應力錨桿支護結構邊坡的地震屈服加速度系數。

3.6 框架預應力錨桿支護結構地震永久位移計算

在Newmark理論[7]中，假定滑塊的位移是被認為是永久位移，將地震時的瞬時地震加速度設為k（t），當k（t）＜k s 時，邊坡不會產生位移；當k（t）=k s 時，邊坡處于極限狀態；當k（t）＞k s 時，邊坡開始移動。以圖7為例，假設地震波形為正弦波，當k（t）增大時，邊坡開始加速，產生位移累計，直至地震加速度最大值；當k（t）逐漸減小時，邊坡開始減速，直到k（t）=k c ，此時，邊坡速度為0，位移為0。

根據前文分析，可以得知地震時某一時刻的邊坡加速度：

對式（42）進行關于t的二次積分，即可得出地震作用下框架預應力錨桿支護結構邊坡永久位移的公式：

通過（43）可得，邊坡的永久位移與地震加速度k（t）、地震屈服加速度k s 有關。因此，在計算地震永久位移時，僅需要確定地震屈服加速度以及地震波即可求得地震作用下框架預應力錨桿支護結構邊坡永久位移。

4 算例驗證

4.1 工程概況

地震水平加速度為 0.3 g，豎向地震及速度取0.1 g。在進行 PLAXIS 3D 進行數值模擬時，選用EI-Centro波對邊坡進行地震作用下的數值模擬，其地震波圖如圖8所示。

4.2 理論計算結果

根據文章的計算方法，基于上一節中的設計參數，得出了邊坡永久位移的結果，將該結果與PLAX?IS 3D 模擬得出的位移結果進行對比分析，運用MATLAB軟件所求得的k s =0.136，所求的永久位移和模擬所得的永久位移見表1。得出以下結論：文章計算方法所得到的邊坡地震永久位移值和PLAXIS 3D模擬所得的永久位移值相差不大，有限元軟件所得的永久位移偏大，因此文章的計算方法偏向于保守。

如圖9、圖10、表1所示，在靜力和地震作用下，采用有限元軟件進行數值模擬計算得到的邊坡位移峰值變化曲線大致相似。中下部結構的位移值較大，而頂部位移值和底部位移值略小于中部位移值。當考慮地震作用時，整體上邊坡位移值增加。然而，由于框架預應力錨桿支護結構中的各體系之間相互協同作用分擔了地震過程中邊坡內的剪力，因此邊坡位移峰值變化的趨勢并沒有太大變化。

5 結論

文章針對框架預應力錨桿支護結構邊坡的位移展開研究，主要運用擬靜力法和極限分析上限法對地震作用下的邊坡位移進行研究，并且通過工程實例對所得的計算方法進行了驗證，得出以下幾點結論：

（1）運用擬靜力法和極限分析上限法對邊坡位移進行計算，首先確定了框架預應力錨桿支護邊坡的計算模型，隨后依據計算模型計算了外力做功和內能耗散情況，求得邊坡地震屈服加速度，最后得出地震作用下邊坡永久位移的計算公式。

（2）通過MATLAB編程軟件對理論計算公式進行計算，并與數值模擬分析結果進行對比驗證，結果表示，該計算方法所得結果相較于有限元模擬值偏大，驗證了公式的有效性與正確性，可為支護設計提供一定的依據。

（3）數值模擬分析表明，框架預應力錨桿支護結構在靜力和地震2種狀態下都能夠控制邊坡的位移，對一定程度上抑制邊坡產生的位移起到了重要的作用。然而，在地震作用下，框架預應力錨桿支護結構的控制作用并不足以完全抵擋邊坡的位移變形。

參考文獻：

[1]朱彥鵬，鄭善義，閻茹，等. 黃土邊坡框架預應力錨桿支擋結構的設計研究[J]. 巖土工程學報，2006（S1）：1582-1585.

[2]周勇，朱彥鵬. 框架預應力錨桿邊坡支護結構頂部靜力位移求解及其所受影響因素分析[J]. 蘭州理工大學學報，2008（2）：113-117.

[3]周勇，朱彥鵬. 框架預應力錨桿柔性支護結構坡面水平位移的理論分析與模型試驗研究[J]. 巖石力學與工程學報，2010，29（S2）：3820-3829.

[4]韓愛民，李建國，肖軍華，等.預應力錨桿框架梁的支護力學行為研究[J]. 巖土力學，2010，31（9）：2894-2900.

[5]王長榮. 黃土地區框架預應力錨桿支護結構研究綜述[J].中國建材科技，2010，19（6）：76-80.

[6]陳祖煜. 土力學經典問題的極限分析上、下限解[J]. 巖土工程學報，2002（1）：1-11.

[7]Newmark N M. Effect of Earthquake on dams and em?bankment[J]. Geotechnique，1965，15（2）：139-160.

Calculation of Permanent Seismic Displacement of Frame Prestressed Bolt Support Structure

LIU Donghan

（Gansu Wuhuan Highway Engineering.，Ltd，Lanzhou Gansu 730050，China）

Abstract： ： The seismic permanent displacement is a key factor to evaluate the seismic performance and safety performance of the structure， especially for the complex flexible support structure such as the frame prestressed bolt support structure， and its value depends on the material properties of the structure， the form and the strength of the seismic action. Therefore， studying the permanent displacement of the support structure under the action of earth?quake has an important influence on improving the seismic capability of the support structure. This paper studies the calculation method of the seismic permanent displacement of the prestressed anchor structure of the frame， ex?plores the deformation rule and seismic capability of the structure under the action of earthquake， and puts forward the feasibility calculation method of the permanent displacement. This paper mainly uses the pseudo-static method，limit analysis upper limit method and other theoretical calculation methods to derive the seismic yield acceleration of the frame prestressed bolt support structure， and calculates the seismic permanent displacement of the structure according to the parameter. The theoretical formula is calculated by MATLAB programming software， and the re?sults are compared with the numerical simulation analysis to verify the effectiveness and correctness of the formula，which can provide a certain basis for the support design.

Key words： ： frame prestressed bolt; supporting structure; upper limit analysis method; seismic permanent dis?placement; finite element simulation