一種改進(jìn)的帶有動(dòng)量的隨機(jī)梯度下降優(yōu)化算法

黃建勇 周躍進(jìn)

【摘?? 要】?? 帶有動(dòng)量的隨機(jī)梯度下降（SGDM）優(yōu)化算法是目前卷積神經(jīng)網(wǎng)絡(luò)（CNNs）訓(xùn)練中最常用的算法之一。然而，隨著神經(jīng)網(wǎng)絡(luò)模型的復(fù)雜化，利用SGDM算法去訓(xùn)練神經(jīng)網(wǎng)絡(luò)模型所需時(shí)間越來(lái)越長(zhǎng)，因此，改進(jìn)SGDM算法的收斂性能是十分必要的。在SGDM算法的基礎(chǔ)上，提出了一種新算法SGDMNorm。新算法利用歷史迭代的梯度范數(shù)對(duì)梯度進(jìn)行校正，在一定程度上提高了SGDM算法的收斂速度。從收斂性的角度對(duì)該算法進(jìn)行分析，證明了SGDMNorm算法具有[O（T）]悔界。通過(guò)數(shù)值模擬實(shí)驗(yàn)和CIFAR-10圖片分類應(yīng)用，表明SGDMNorm算法收斂速度比SGDM算法更快。

【關(guān)鍵詞】?? 梯度下降算法；神經(jīng)網(wǎng)絡(luò)；梯度范數(shù)；分類

An Improved Stochastic Gradient Descent

Optimization Algorithm with Momentum

Huang Jianyong，Zhou Yuejin*

（Anhui University of Science and Technology， Huainan 232001， China）

【Abstract】??? Stochastic gradient descent optimization algorithm with momentum （SGDM） is currently one of the most commonly used optimization algorithms for training convolutional neural networks （CNNs）. However， as neural network models become more complex， the time which needs to train them by using the SGDM algorithm also increases. Therefore， it is very necessary to improve the convergence performance of SGDM algorithm. In this paper， we propose a new algorithm called SGDMNorm based on the SGDM algorithm. The new algorithm corrects gradients by using the gradient norm of historical iterations， which improves the convergence speed of the SGDM algorithm. Then， we analyze the algorithm from the perspective of convergence and prove that the SGDMNorm algorithm has a regret bound of [O（T）]. Finally， the numerical simulations and CIFAR-10 image classification applications demonstrate that the SGDMNorm algorithm converges faster than the SGDM algorithm.

【Key words】???? gradient descent algorithm; neural networks; gradient norm; classification

〔中圖分類號(hào)〕?? TP183?????????????????????????????? 〔文獻(xiàn)標(biāo)識(shí)碼〕? A? ???????????? 〔文章編號(hào)〕 1674 - 3229（2024）02- 0036 - 09

[收稿日期]?? 2024-01-08

[基金項(xiàng)目]?? 深部煤礦采動(dòng)響應(yīng)與災(zāi)害防控國(guó)家重點(diǎn)實(shí)驗(yàn)室基金資助項(xiàng)目（SKLMRDPC22KF03）

[作者簡(jiǎn)介]?? 黃建勇（1999- ），男，安徽理工大學(xué)數(shù)學(xué)與大數(shù)據(jù)學(xué)院碩士研究生，研究方向：統(tǒng)計(jì)機(jī)器學(xué)習(xí)。

[通訊作者]?? 周躍進(jìn)（1977- ），男，博士，安徽理工大學(xué)數(shù)學(xué)與大數(shù)據(jù)學(xué)院教授，研究方向：統(tǒng)計(jì)機(jī)器學(xué)習(xí)、因果推斷。

0???? 引言

近年來(lái)，卷積神經(jīng)網(wǎng)絡(luò)（Convolutional Neural Networks，CNNs）已經(jīng)成為解決計(jì)算機(jī)視覺(jué)問(wèn)題的主要參數(shù)模型［1-3］。然而，隨著數(shù)據(jù)集的增大和神經(jīng)網(wǎng)絡(luò)層數(shù)的增加，模型的訓(xùn)練愈發(fā)困難。所以研究一個(gè)收斂性能較好的神經(jīng)網(wǎng)絡(luò)模型優(yōu)化算法尤其重要。CNNs模型通常使用基于小批量樣本批處理的隨機(jī)梯度下降（Stochastic Gradient Descent，SGD）優(yōu)化算法進(jìn)行訓(xùn)練。利用SGD算法訓(xùn)練神經(jīng)網(wǎng)絡(luò)模型具有操作簡(jiǎn)單、占用計(jì)算機(jī)內(nèi)存小等優(yōu)點(diǎn)。但是，SGD算法也有缺點(diǎn)，其參數(shù)更新僅受當(dāng)前隨機(jī)抽取的小批量樣本的平均梯度影響［4］。若其中某些樣本特性差異較大，參數(shù)更新方向可能會(huì)不一致，導(dǎo)致在實(shí)際應(yīng)用中SGD優(yōu)化算法收斂速度慢。

為了改進(jìn)上述SGD算法，很多基于SGD的優(yōu)化算法先后被提出。根據(jù)是否使用自適應(yīng)學(xué)習(xí)率，可以將這些改進(jìn)的優(yōu)化算法分為兩類。第一類是非自適應(yīng)學(xué)習(xí)率優(yōu)化算法，即所有參數(shù)的更新使用同一個(gè)學(xué)習(xí)率。其中，SGDM（SGD with Momentum）優(yōu)化算法利用每個(gè)小批量樣本平均梯度的指數(shù)滑動(dòng)平均來(lái)更新參數(shù)，有效改進(jìn)了SGD優(yōu)化算法收斂速度慢、在局部最小值和鞍點(diǎn)處不更新的問(wèn)題［5］。此外，袁煒和胡飛在SGDM算法的基礎(chǔ)上，提出了RSGDM（Rectified SGDM）優(yōu)化算法，該算法利用差分估計(jì)項(xiàng)來(lái)修正SGDM算法中一階動(dòng)量的偏差和滯后性［6］。第二類是自適應(yīng)學(xué)習(xí)率優(yōu)化算法，即不同參數(shù)使用不同的學(xué)習(xí)率。例如Adam（Adaptive Moment Estimation）優(yōu)化算法結(jié)合了SGDM和RMSProp（Root Mean Square Propogation）的思想，利用一階動(dòng)量來(lái)更新參數(shù)、二階動(dòng)量來(lái)控制學(xué)習(xí)率［7］。由于Adam算法較其他算法而言，收斂速度更快，目前已被廣泛用于不同的神經(jīng)網(wǎng)絡(luò)模型，來(lái)解決不同的計(jì)算機(jī)視覺(jué)問(wèn)題。但是，在實(shí)際應(yīng)用時(shí)該算法大多只能收斂到局部最優(yōu)值點(diǎn)。為了解決該問(wèn)題，Radam（Rectified Adam）優(yōu)化算法根據(jù)方差分散度，動(dòng)態(tài)地打開或關(guān)閉自適應(yīng)學(xué)習(xí)率，在一定程度上緩解了Adam優(yōu)化算法收斂到局部最優(yōu)解的問(wèn)題［8］。

目前，很多神經(jīng)網(wǎng)絡(luò)模型使用第二類自適應(yīng)學(xué)習(xí)率優(yōu)化算法進(jìn)行訓(xùn)練。雖然這類算法在訓(xùn)練集上的收斂速度較快，但是在測(cè)試集上準(zhǔn)確率較差，泛化能力不如SGDM［9-10］。SGDM算法較這些自適應(yīng)優(yōu)化算法而言，最大的缺陷是在訓(xùn)練集上收斂速度較慢。因此，本文在SGDM算法的基礎(chǔ)上，利用歷史迭代的梯度范數(shù)對(duì)當(dāng)前梯度進(jìn)行校正。經(jīng)過(guò)校正，可以有效提高SGDM算法在訓(xùn)練集上的收斂速度。

1???? SGDMNorm算法

在基于小批量樣本處理的SGDM算法中，首先隨機(jī)抽取一批樣本并計(jì)算其平均梯度，即：

[gt=1Bb=1B? θtf（xb，θt）]，????? （1）

其中[x1，x2，...，xB]表示在迭代訓(xùn)練中抽取的小批量樣本；[B]表示抽取的小批量樣本數(shù)； [θt]表示第[t]次迭代訓(xùn)練時(shí)的模型參數(shù)；[?]? 表示在[θt]處的梯度；[gt]表示第[t]次迭代訓(xùn)練時(shí)小批量樣本的平均梯度。

然后，利用平均梯度的指數(shù)滑動(dòng)平均計(jì)算動(dòng)量，即：

[mt=βtmt-1+（1-βt）gt]?????????????? ?? ??????????（2）

其中[mt]是第[t]次迭代訓(xùn)練時(shí)的動(dòng)量，其初始值[m0=0]；[βt∈[0，1）]是指數(shù)衰減率（一般設(shè)為0.9）。

最后，對(duì)參數(shù)進(jìn)行更新，即：

[θt+1=θt-αtmt] （3）

其中[αt]表示第[t]次更新參數(shù)時(shí)所用步長(zhǎng)，也稱為學(xué)習(xí)率。

本文所提的SGDMNorm算法在SGDM算法的基礎(chǔ)上增加了一個(gè)梯度校正項(xiàng)，具體如下所示。首先，計(jì)算[gt]的[l2]范數(shù)，即：

[gt，norm=i=1kg2t，i]?? （4）

其中[gt，norm]表示[gt]的[l2]范數(shù)；[gt，i]表示[gt]的第[i]個(gè)元素；[k]表示向量[gt]中的元素個(gè)數(shù)。

然后，利用歷史梯度范數(shù)對(duì)當(dāng)前梯度進(jìn)行校正，即：

[et=γet-1+（1-γ）gt，norm]???????????????????? ? （5）

[st=（etgt，norm+ε）ηtgt，if et>gt，normgt???????????????????? ，otherwise]? ????? ?（6）

其中[et]表示第[t]次迭代訓(xùn)練時(shí)的歷史梯度范數(shù)，其初始值[e0=0]；[st]表示校正后的梯度； [ηt∈1，2]是參數(shù)，隨迭代訓(xùn)練次數(shù)衰減，默認(rèn)取[ηt=（1+1t）]；[γ∈0，1]是參數(shù)，根據(jù)經(jīng)驗(yàn)，[γ]取值為0.95時(shí)效果比較好；[ε]是一個(gè)任意小的正數(shù)，使得[gt，norm+ε≠0]。

以某一函數(shù)為例，該函數(shù)圖像如圖1所示，可以看出在A和C點(diǎn)附近梯度及其[l2]范數(shù)都比較大；在B和D點(diǎn)附近梯度及其[l2]范數(shù)都比較小。因此，根據(jù)本文所提出的梯度校正方法，B和D點(diǎn)附近參數(shù)將會(huì)使用更大的梯度進(jìn)行更新，從而更快收斂到最小值點(diǎn)。

SGDMNorm算法具體實(shí)現(xiàn)步驟如下：

步驟1?? 選擇超參數(shù)：[αt=0.01]（學(xué)習(xí)率），[βt=0.9]，[γ=0.95]，[ηt=（1+1t）]，[ε=10-16]。

步驟2?? 模型初始化：[m0←0]，[e0←0]，[t←0]，[θ0]。

步驟3?? 判斷是否滿足終止條件，不滿足條件重復(fù)執(zhí)行步驟4-10，滿足則輸出[θt+1]。

步驟4?? 更新迭代次數(shù)：[t←t+1]。

步驟5?? 計(jì)算平均梯度：[gt=1Bb=1B?? f（xb，θt）]。

步驟6?? 計(jì)算當(dāng)前梯度范數(shù)：[gt，norm=i=1kg2t，i]。

步驟7?? 更新歷史梯度范數(shù)：[et=γet-1+（1-γ）gt，norm。]

步驟8?? 判斷是否進(jìn)行梯度校正：

[st=（etgt，norm+ε）ηtgt，if et>gt，normgt??????????? ?????????，otherwise]。

步驟9?? 更新動(dòng)量：[mt=βtmt-1+（1-βt）st]。

步驟10?? 更新參數(shù)：[θt+1=θt-αtmt]。

2???? SGDMNorm算法收斂性分析

利用Zinkevich提出的在線學(xué)習(xí)框架分析SGDMNorm算法的收斂性［11］。假設(shè)任意未知的凸損失函數(shù)序列[f1（θ），f2（θ），...，fT（θ）]，目的是預(yù)測(cè)每次迭代（第[t]步）的參數(shù)[θt]，[t=1，2，...，T]，并計(jì)算在該點(diǎn)處的函數(shù)[ft（θt）]。對(duì)于此類未知的凸損失函數(shù)序列，算法可基于悔界進(jìn)行分析計(jì)算。從解空間[χ]中計(jì)算一個(gè)在線猜測(cè)損失函數(shù)[ft（θt）]和一個(gè)期望損失函數(shù)[ft（θ*）]，其中

[θ*=argminθ∈χt=1Tft（θ）]

并計(jì)算二者之間的誤差，悔界的定義為誤差的總和，其表達(dá)式如下所示

[R（T）=t=1T（ft（θt）-ft（θ*））]

在這種情況下，可以證明SGDMNorm算法的悔界為[O（T）]。

定理1?? 假設(shè)函數(shù)[ft]的梯度有界且由SGDMNorm算法生成的任意點(diǎn)[θt]之間的距離有界，即對(duì)[?θ∈Rd]，有[?ft（θ）2≤G]， [?ft（θ）∞≤G∞]；且對(duì)[?m，n∈1，2，...，T]，有[θm-θn2≤D2]，[θm-θn∞≤D∞]。令[αt=αt]，[βt=βt]，則有[R（T）≤D2∞2（1-β1）i=1d1αT+KG∞D(zhuǎn)∞1-β1][i=1dt=1Tβt+]

[K2G2∞2（1-β1）i=1dt=1Tαt]。

證明：由文獻(xiàn)［7］中引理10.2有

[ft（θt）-ft（θ*）≤（gTt，θt-θ*）=i=1dgt，i（θt，i-θ*i）]，

其中[gt，i]是[θ]的第[i]個(gè)元素在第[t]次迭代訓(xùn)練時(shí)的梯度。

根據(jù)算法1的更新規(guī)則有

[θt+1=θt-αtmt=θt-αt[βtmt-1+（1-βt）st）] 。]

根據(jù)梯度校正規(guī)則，可以得到

[et=γet-1+（1-γ）gt，norm?? =γ[γet-2+（1-γ）gt-1，norm]+（1-γ）gt，norm?? =j=1t（1-γ）γt-jgj，norm 。]

根據(jù)梯度有界假設(shè)，經(jīng)過(guò)放縮后得到[et≤（1-γt）G≤G]。

令[lt=（etgt，norm+ε）ηt，if et>gt，norm1???????????????????? ，otherwise]。因?yàn)閇gt，norm≤G]，[1≤ηt≤2]，均是有界量，所以[lt]有界。假設(shè)上界為[K]，由此可得[1≤lt≤K]。

將參數(shù)向量[θt+1]第[i]個(gè)元素與[θ*]的第[i]個(gè)元素做差，并平方可得

[（θt+1，i-θ*i）2=（θt，i-θ*i）2-2αt[βtmt-1，i+（1-βt）st，i]（θt，i-θ*i）][+α2tm2t，i]，

其中[mt，i]是[mt]的第[i]個(gè)元素在第[t]次迭代訓(xùn)練時(shí)的動(dòng)量。

因?yàn)閇st，i=ltgt，i]，所以上式可以表示成

[（θt+1，i-θ*i）2=（θt，i-θ*i）2-2αt[βtmt-1，i+（1-βt）ltgt，i]（θt，i-θ*i）][+α2tm2t，i]，

將上式整理后，得到[gt，i（θt，i-θ*i）=]

[（θt，i-θ*i）2-（θt+1，i-θ*i）22αt（1-βt）lt+βtmt-1，i（θt，i-θ*i）（1-βt）lt+][αtm2t，i2（1-βt）lt]。

對(duì)[ft（θt）-ft（θ*）]在[i∈1，...，d]的上界在[t=1，2，...，T]的累加求和，得出悔界滿足

[R（T）≤i=1dt=1T（θt，i-θ*i）2-（θt+1，i-θ*i）22αt（1-βt）lt+] [i=1dt=1Tβtmt-1，i（θt，i-θ*i）（1-βt）lt][+i=1dt=1Tαtm2t，i2（1-βt）lt]????? （7）

接下來(lái)依次對(duì)上式右邊三個(gè)單項(xiàng)式分別進(jìn)行放縮。

1）首先對(duì)（7）式中的第一個(gè)單項(xiàng)式放縮，因?yàn)閇lt≥1]，[β1>βT]所以有

[i=1dt=1T（θt，i-θ*i）2-（θt+1，i-θ*i）22αt（1-βt）lt≤i=1dt=1T（θt，i-θ*i）2-（θt+1，i-θ*i）22αt（1-βt）≤i=1dt=1T（θt，i-θ*i）2-（θt+1，i-θ*i）22αt（1-β1）， ]

接著使用錯(cuò)位相減進(jìn)行放縮，得到

[i=1dt=1T（θt，i-θ*i）2-（θt+1，i-θ*i）22αt（1-β1）=i=1dt=1T（θt，i-θ*i）22αt（1-β1）-t=1T（θt+1，i-θ*i）22αt（1-β1）]

[=i=1d[（θ1，i-θ*i）22α1（1-β1）+t=1T-1（（θt+1，i-θ*i）22αt+1（1-β1）-（θt+1，i-θ*i）22αt（1-β1））-（θT+1，i-θ*i）22αT（1-β1）]≤i=1d[D2∞2α1（1-β1）+D2∞1-β1t=1T-1（12αt+1-12αt）]=D2∞i=1d12αT（1-β1）=D2∞2（1-β1）i=1d1αT 。]

在對(duì)第二和第三個(gè)單項(xiàng)式放縮前，首先對(duì)[mt，i]進(jìn)行放縮，根據(jù)[mt，i]的更新方式可以得到

[mt，i=βtmt-1，i+（1-βt）st，i=βt[βt-1mt-2，i+（1-βt-1）st-1，i]+（1-βt）st，i=k=1t（1-βk）sk，ij=k+1tβj ]，

根據(jù)[lt≤K]和梯度有界假設(shè)，顯然[sk，i≤KG∞]，所以可得

[mt，i≤k=1t（1-βk）KG∞j=k+1tβj=KG∞（1-k=1tβk）≤KG∞]。

2）然后對(duì)（7）式中第二個(gè)單項(xiàng)式放縮，根據(jù)[lt≥1]和[β1>βT]可得

[i=1dt=1Tβtmt-1，i（θt，i-θ*i）（1-βt）lt≤i=1dt=1Tβtmt-1，i（θt，i-θ*i）1-βt≤i=1dt=1Tβtmt-1，i（θt，i-θ*i）1-β1≤KG∞D(zhuǎn)∞1-β1i=1dt=1Tβt。 ]

3）最后對(duì)（7）式中第三個(gè)單項(xiàng)式放縮，根據(jù)[lt≥1]和[β1>βT]可得

[i=1dt=1Tαtm2t，i2（1-βt）lt≤i=1dt=1Tαtm2t，i2（1-βt）≤i=1dt=1Tαtm2t，i2（1-β1）=K2G2∞2（1-β1）i=1dt=1Tαt ， ]

最終經(jīng)過(guò)整理后得到

[R（T）≤D2∞2（1-β1）i=1d1αT+KG∞D(zhuǎn)∞1-β1i=1dt=1Tβt+K2G2∞2（1-β1）i=1dt=1Tαt]。

推論1?? 假設(shè)函數(shù)[ft]的梯度有界且由SGDMNorm算法生成的任意點(diǎn)[θt]之間的距離有界，即對(duì)[?θ∈Rd]，有[?ft（θ）2≤G]，[?ft（θ）∞≤G∞]；且對(duì)[?m，n∈1，2，...，T]，有[θm-θn2≤D2]，[θm-θn∞≤D∞]。若假設(shè)成立，則SGDMNorm算法對(duì)[?T≥1]有[R（T）T=O（1T）]，因此，[limT→∞R（T）T=0]。

3???? 仿真實(shí)驗(yàn)

下面通過(guò)仿真實(shí)驗(yàn)來(lái)驗(yàn)證SGDNorm算法的收斂性能。首先基于python語(yǔ)言sklearn庫(kù)中的make_classification函數(shù)生成一個(gè)分類數(shù)據(jù)集，類別數(shù)是10個(gè)。數(shù)據(jù)集共有40 000個(gè)數(shù)據(jù)，每個(gè)數(shù)據(jù)均有32個(gè)特征。make_classification函數(shù)中具體參數(shù)設(shè)置如表1所示，表中未出現(xiàn)參數(shù)均使用默認(rèn)參數(shù)。

基于pytorch深度學(xué)習(xí)框架，搭建如表2所示的5層全連接神經(jīng)網(wǎng)絡(luò)模型，將SGDM算法與SGDMNorm算法在該模型上進(jìn)行實(shí)驗(yàn)對(duì)比。其中激活函數(shù)均使用Relu，學(xué)習(xí)率設(shè)為0.001，批樣本量設(shè)為256，其余參數(shù)使用前文默認(rèn)參數(shù)，迭代訓(xùn)練1580次。每迭代訓(xùn)練一次就計(jì)算一次損失函數(shù)值，并在訓(xùn)練集上計(jì)算一次準(zhǔn)確率。最后繪制出訓(xùn)練損失和準(zhǔn)確率曲線，如圖2所示。

圖2（a）是訓(xùn)練損失曲線，橫軸表示迭代次數(shù)，縱軸表示損失函數(shù)值。可以看出兩種優(yōu)化算法的損失曲線幾乎重合，都有較大波動(dòng)性。圖2（b）是訓(xùn)練準(zhǔn)確率曲線，橫軸表示迭代次數(shù)，縱軸表示訓(xùn)練準(zhǔn)確率。可以看出在迭代400次后，SGDMNorm算法的訓(xùn)練準(zhǔn)確率開始高于SGDM算法，直到訓(xùn)練結(jié)束，而且很明顯SGDMNorm算法的訓(xùn)練準(zhǔn)確率比SGDM算法更穩(wěn)定，波動(dòng)程度較小。所以，SGDMNorm算法收斂速度比SGDM算法快。

4???? 實(shí)例應(yīng)用

為了進(jìn)一步探究SGDMNorm優(yōu)化算法在實(shí)際應(yīng)用中的有效性，以及學(xué)習(xí)率和小批量樣本數(shù)的大小對(duì)該算法的影響，通過(guò)CIFAR-10圖片分類應(yīng)用比較SGDMNorm算法與SGDM算法的性能。

4.1?? 數(shù)據(jù)集介紹

本文實(shí)驗(yàn)所使用的數(shù)據(jù)集是CIFAR-10數(shù)據(jù)集。該數(shù)據(jù)集共有10個(gè)不同類別的6萬(wàn)張RGB彩色圖像（圖片尺寸為32×32×3），其中有飛機(jī)、輪船、貓、狗和鳥類等。每個(gè)類別各有6000張RGB圖像，每個(gè)類別中取出5000張作為訓(xùn)練集（共50 000張），余下1000張作為測(cè)試集（共10 000張）。

4.2?? 模型設(shè)計(jì)

VGG16卷積神經(jīng)網(wǎng)絡(luò)模型共包括13個(gè)卷積層、5個(gè)池化層以及3個(gè)全連接層。整個(gè)網(wǎng)絡(luò)均采用寬高尺寸為3×3的小卷積核來(lái)提取特征，激活函數(shù)均使用Relu［12］。本文在VGG16卷積神經(jīng)網(wǎng)絡(luò)模型的基礎(chǔ)上，使用pytorch框架，基于CIFAR-10數(shù)據(jù)集搭建了以下兩種不同的模型。

模型1是輕量化模型，采用了5個(gè)卷積層、5個(gè)池化層以及3個(gè)全連接層。整個(gè)網(wǎng)絡(luò)全部使用寬高尺寸為3×3的小卷積核來(lái)提取特征，激活函數(shù)均使用Relu。模型如圖3所示。

模型2則是一個(gè)較為復(fù)雜的模型，卷積層和池化層均和標(biāo)準(zhǔn)VGG16模型一樣，即13個(gè)卷積層和5個(gè)池化層，全連接層則只有一層，激活函數(shù)均使用Relu。模型如圖4所示。

4.3?? 實(shí)驗(yàn)結(jié)果與結(jié)論

為了探究不同學(xué)習(xí)率和小批量樣本數(shù)對(duì)SGDMNorm算法的影響，以及該算法在不同神經(jīng)網(wǎng)絡(luò)模型中的適用性，設(shè)置以下兩組對(duì)比實(shí)驗(yàn)。

（1）實(shí)驗(yàn)1（探究不同小批量樣本數(shù)對(duì)SGDMNorm算法的影響）：將小批量樣本數(shù)分別設(shè)為64、128和256，學(xué)習(xí)率均設(shè)為0.001，指數(shù)衰減率均設(shè)為0.9，其他參數(shù)均使用前文所提默認(rèn)值，分別迭代訓(xùn)練780次，使用模型1進(jìn)行實(shí)驗(yàn)。

（2）實(shí)驗(yàn)2（探究不同學(xué)習(xí)率對(duì)SGDMNorm算法的影響）：將學(xué)習(xí)率分別設(shè)為0.001、0.005和0.01，小批量樣本數(shù)均設(shè)為256，指數(shù)衰減率均設(shè)為0.9，其他參數(shù)均使用前文所提默認(rèn)值，分別迭代訓(xùn)練980次，使用模型2進(jìn)行實(shí)驗(yàn)。

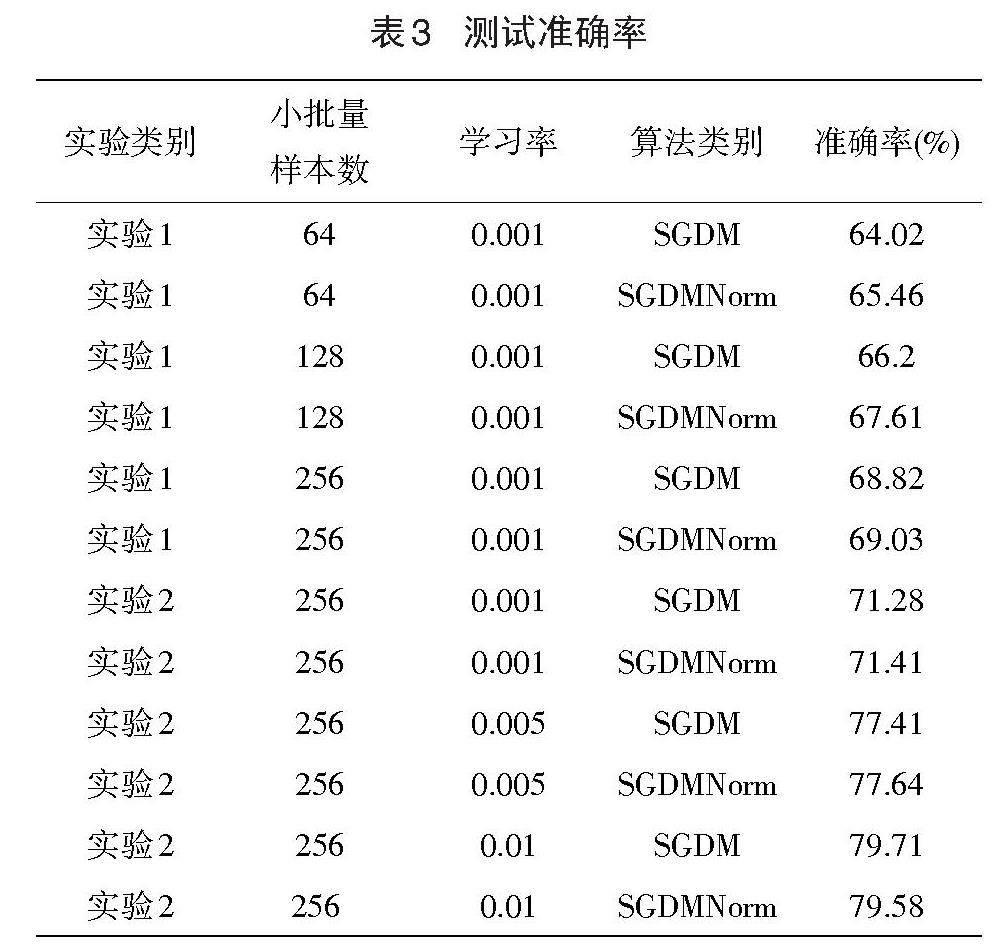
通過(guò)以上兩組實(shí)驗(yàn)的設(shè)計(jì)，對(duì)SGDMNorm算法和SGDM算法進(jìn)行實(shí)驗(yàn)對(duì)比。每迭代訓(xùn)練一次就計(jì)算一次損失函數(shù)值，并在訓(xùn)練集上計(jì)算一次準(zhǔn)確率，繪制出訓(xùn)練損失和準(zhǔn)確率曲線，如圖5-8所示。訓(xùn)練結(jié)束后，在測(cè)試集進(jìn)行上測(cè)試，測(cè)試準(zhǔn)確率在表3中給出。

圖5給出了不同小批量樣本數(shù)的訓(xùn)練損失曲線，a、b、c三個(gè)子圖分別對(duì)應(yīng)小批量樣本數(shù)為64、128和256時(shí)的訓(xùn)練數(shù)據(jù)，橫軸均表示迭代次數(shù)，縱軸均表示損失函數(shù)值。從a、b、c三圖可以看出兩種算法的損失函數(shù)值收斂速度大體相同。但是，很明顯SGDMNorm算法的損失函數(shù)值的波動(dòng)性更小、更穩(wěn)定。

圖6給出了不同小批量樣本數(shù)的訓(xùn)練準(zhǔn)確率曲線，a、b、c三個(gè)子圖分別對(duì)應(yīng)小批量樣本數(shù)為64、128和256時(shí)的訓(xùn)練數(shù)據(jù)，橫軸均表示迭代次數(shù)，縱軸均表示訓(xùn)練準(zhǔn)確率。對(duì)于a圖，可以看出在迭代50次后，SGDMNorm算法的訓(xùn)練準(zhǔn)確率開始高于SGDM算法，直到訓(xùn)練結(jié)束。對(duì)于b和c圖，可以看出在整個(gè)迭代訓(xùn)練過(guò)程中，兩種算法的收斂速度差不多，但是，SGDMNorm算法的訓(xùn)練準(zhǔn)確率大多時(shí)候略優(yōu)于SGDM算法。總的來(lái)說(shuō)，在不同小批量樣本數(shù)下，都是SGDMNorm算法準(zhǔn)確率更高、收斂速度更快且穩(wěn)定性更好。此外，可以看出較SGDM算法而言，SGDMNorm算法可以有效避免樣本數(shù)過(guò)小而導(dǎo)致的模型訓(xùn)練過(guò)程中的不穩(wěn)定。

圖7給出了不同學(xué)習(xí)率的訓(xùn)練損失曲線，a、b、c三個(gè)子圖分別對(duì)應(yīng)學(xué)習(xí)率為0.001、0.005和0.01時(shí)的訓(xùn)練數(shù)據(jù)，橫軸均表示迭代次數(shù)，縱軸均表示損失函數(shù)值。從a和b圖可以看出，對(duì)于較小的學(xué)習(xí)率，兩種算法的訓(xùn)練損失函數(shù)值收斂速度大體相同，兩種算法的損失曲線幾乎重合。從c圖可以看出，對(duì)于較大的學(xué)習(xí)率，SGDMNorm算法損失函數(shù)值收斂速度略快于SGDM算法，且波動(dòng)性較小。

圖8給出了不同學(xué)習(xí)率的訓(xùn)練準(zhǔn)確率曲線，a、b、c三個(gè)子圖分別對(duì)應(yīng)學(xué)習(xí)率為0.001、0.005和0.01時(shí)的訓(xùn)練數(shù)據(jù)，橫軸均表示迭代次數(shù)，縱軸均表示訓(xùn)練準(zhǔn)確率。對(duì)于a圖，可以看出兩種算法的訓(xùn)練準(zhǔn)確率曲線在整個(gè)迭代訓(xùn)練過(guò)程幾乎重合。對(duì)于b圖，可以看出在迭代200次前，SGDMNorm算法的訓(xùn)練準(zhǔn)確率和SGDM算法相差不大；在迭代200次后，SGDMNorm算法的訓(xùn)練準(zhǔn)確率略高于SGDM算法；在迭代900次后，兩種算法收斂速度幾乎相同。對(duì)于c圖，可以看出在迭代50次后，SGDMNorm算法訓(xùn)練準(zhǔn)確率開始高于SGDM算法，直到訓(xùn)練結(jié)束，而且很明顯SGDMNorm算法的穩(wěn)定性更好，準(zhǔn)確率曲線波動(dòng)性更小。總的來(lái)說(shuō)，可以看出在學(xué)習(xí)率較大的情況下，兩種算法的差距較為明顯，SGDMNorm算法的優(yōu)化性能比SGDM算法的優(yōu)化性能更好，在訓(xùn)練過(guò)程中的波動(dòng)性更小。在學(xué)習(xí)率較小的情況下，兩種算法差距較小，優(yōu)化性能幾乎相同。

表3給出了兩種優(yōu)化算法在CIFAR-10測(cè)試集上的測(cè)試準(zhǔn)確率。通過(guò)實(shí)驗(yàn)1可以看出在同一學(xué)習(xí)率、不同小批量樣本數(shù)的條件下，都是SGDMNorm算法測(cè)試準(zhǔn)確率更高。在小批量樣本數(shù)為64的情況下，兩種算法的測(cè)試準(zhǔn)確率差距最大，SGDMNorm算法測(cè)試準(zhǔn)確率比SGDM算法提高了1.44個(gè)百分點(diǎn)。通過(guò)實(shí)驗(yàn)2可以看出在不同學(xué)習(xí)率、相同小批量樣本數(shù)的條件下，兩種算法測(cè)試準(zhǔn)確率差距不大。當(dāng)學(xué)習(xí)率較小時(shí)，SGDMNorm算法測(cè)試準(zhǔn)確率略高于SGDM算法。當(dāng)學(xué)習(xí)率較大時(shí)，SGDMNorm算法可能有過(guò)擬合的風(fēng)險(xiǎn)，導(dǎo)致其測(cè)試準(zhǔn)確率稍低于SGDM算法。

5???? 結(jié)語(yǔ)

近年來(lái)，面對(duì)越來(lái)越多且越來(lái)越復(fù)雜的數(shù)據(jù)，深度神經(jīng)網(wǎng)絡(luò)模型因其良好的數(shù)據(jù)處理能力引起學(xué)界的廣泛關(guān)注。但是，隨著數(shù)據(jù)集的增大、神經(jīng)網(wǎng)絡(luò)模型層數(shù)的增加以及模型的不斷復(fù)雜化，高效快速地訓(xùn)練一個(gè)高精度的模型變得愈發(fā)困難。因此一個(gè)好的優(yōu)化算法對(duì)模型的訓(xùn)練有著至關(guān)重要的作用。首先，本文在SGDM算法的基礎(chǔ)上，利用歷史迭代的梯度范數(shù)對(duì)梯度進(jìn)行校正，提出了SGDMNorm算法。其次，證明了SGDMNorm優(yōu)化算法具有[O（T）]悔界。再次，在CIFAR-10數(shù)據(jù)集上進(jìn)行圖像分類實(shí)驗(yàn)，實(shí)驗(yàn)結(jié)果進(jìn)一步表明SGDMNorm算法具有更好的收斂性能。在未來(lái)，也可將這種基于歷史梯度范數(shù)對(duì)梯度進(jìn)行校正的思想應(yīng)用到一些自適應(yīng)梯度下降優(yōu)化算法中。

［參考文獻(xiàn)］

［1］ Lecun Y，Bengio Y，Hinton G. Deep learning ［J］. Nature，2015，521（7553）：436-444.

［2］ Jaffeux L，Schwarzenb?ck A，Coutris P，et al. Ice crystal images from optical array probes： classification with convolutional neural networks［J］. Atmospheric Measurement Techniques，2022，15（17）：5141-5157.

［3］Ren S，He K，Girshick R，et al. Faster r-cnn： towards real-time object detection with region proposal networks［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence，2017，39（6）：1137-1149.

［4］ Bottou L. Large-scale machine learning with stochastic gradient descent［A］.?Peter M. The Nineteenth International Conference on Computational Statistics［C］. Amsterdam：Elsevier Press，2010：177-186.

［5］ Qian N. On the momentum term in gradient descent learning algorithms［J］. Neural Networks the Official Journal of the International Neural Network Society，1999，12（1）：145-151.

［6］ 袁煒，胡飛.基于差分修正的SGDM算法［J］.計(jì)算機(jī)系統(tǒng)應(yīng)用，2021，30（7）：220-224.

［7］ Kingma D P，Ba J. Adam： a method for stochastic optimization［A］. Bengio Y. The third International Conference on Learning Representations［C］. London：Academic Press，2015：1142-1156.

［8］ Liu L，Jiang H，He P，et al. On the variance of the adaptive learning rate and beyond［A］. Lecun Y. The Eighth International Conference for Learing Repre sentations［C］. London：Academic Press，2020：1358-1371.

［9］ 姜志俠，宋佳帥，劉宇寧.一種改進(jìn)的自適應(yīng)動(dòng)量梯度下降算法［J］.華中科技大學(xué)學(xué)報(bào)（自然科學(xué)版），2023，51（5）：137-143.

［10］??? Dubey S R，Chakraborty S，Roy S K，et al. Diffgrad： an optimization method for convolutional neural networks［J］. IEEE Transactions on Neural Networks and Learning Systems，2019，19（31）：4500-4511.

［11］??? Zinkevich M. Online convex programming and generalized infinitesimal gradient ascent［A］. Tom F. The Twentieth International Conference on Machine Learning［C］. Menlo Park：Association for the Advancement of Artificial Intelligence Press，2003：928-936.

［12］??? Simonyan K，Zisserman A. Very deep convolutional networks for large-scale image recognition［A］. Bengio Y. The Third International Conference on Learning Representations［C］. London：Academic Press，2015：637-649.