數形結合：可視化演繹“數與運算”的一致性

作者簡介：單廣紅，江蘇省淮安市浦東實驗小學特級教師，正高級教師。

課題項目：本文系江蘇省教育科學“十四五”規劃2021年度課題“基于‘童化’視域的小學數學鑲嵌式學習研究”的階段性研究成果。課題編號：D/2021/02/324。

摘要：“數與運算”的一致性主要包括數概念的一致性、運算意義的一致性、算理算法的一致性。在課堂教學中落實“數與運算”的一致性，需要教師在一定的學習時段靈活、統籌安排。在第二學段學習完整數除法單元內容后，教師可以設計“整數四則運算再認識”一課的教學，引導學生理解整數四則運算在算理和算法上的一致性。

關鍵詞：數形結合；數與運算；一致性；算理；算法

《義務教育數學課程標準（2022年版）》（以下通稱“新課標”）指出：“數的運算教學應注重對整數、小數和分數四則運算的統籌，讓學生進一步感悟運算的一致性。”“數與代數”領域包括“數與運算”和“數量關系”兩大學習主題。“數與運算”是一個較為龐大的話題體系，包括三個方面：數概念的一致性、運算意義的一致性、算理算法的一致性。整數、小數、分數等數概念及其運算學習內容零散分布在各學段，跨度較大，需要教師靈活統整教學內容，讓學生打通“數概念”與“數運算”內部之間的“隔斷”，自主遷移經驗。在第二學段學習完整數除法單元后，教師可以設計“整數四則運算zu4JickG1GQkUYjrLCevJ1T7dJ9ZaaxuT8q+AJixBJc=再認識”一課的教學，引導學生理解整數四則運算在算理和算法上的一致性。

一、感受加減法相同計數單位的簡單線性增減

加法是將不同兩部分或幾部分合并在一起的運算。減法、乘法、除法都是由加法衍生而來的。整數加法是四則運算的基礎，需要學生理解透徹其算理和算法，然后類比遷移到其他運算中。

（一）整數計數：建構計數直觀模型的十進制原理

數是對數量的抽象，認數的目的是解決計算問題。計數本身就是加法運算，如238是由2個百、3個十和8個一組成的，其實就是200 + 30 + 8 = 238，相鄰計數單位之間因存在“十進制”的特殊關系而產生了特定的“位值”。

<E：＼2023田田＼7-20＼遼寧教育·教研版202407＼LJ24-13-1.psd>

計數：2個百、3個十和8個一合起來是238。

計算：200 + 30 + 8 = 238。

為了數數方便，由“一個一個地數”到“一群一群地數”，整數計數便成為關于計數單位的加法運算。因此，對數概念的學習基礎直接影響到數運算的算法算理理解。整數的計數單位有個、十、百、千、萬等，每個計數單位都對應著一個數學模型。常用的數學模型有小棒、小正方體、小方塊、計數器等，在小學階段呈現的最大的可視化計數單位數學模型是由小正方體拼成的“萬”，更大的單位則需要依據基本的計數單位去抽象推理。為了方便溝通“數與運算”的一致性，本文均選用平面方塊圖作為圖例。

（二）整數加法：掌握啟蒙計算圖式的可視化表達

小學階段的學生對算理理解的表象水平一般用三種圖式表示：實物圖式、半抽象圖式和符號圖式。在教學中，教師要給足時間讓學生對算理進行可視化表達，使其能準確進行互譯解讀。例如，在“整數四則運算再認識”的課始，教師可以喚醒學生的加法算理。

師：請用你喜歡的方式表示“371 + 54”的計算過程。

生：我用估算，371 ≈ 380，54 ≈ 50，它們的和大約是四百。

生：我是用口算計算的，1 + 4 = 5，70 + 50 = 120，300 + 120 + 5 = （300 + 100） + 20 + 5 = 425。

生：我是通過貼方塊圖來計算的。

<E：＼2023田田＼7-20＼遼寧教育·教研版202407＼LJ24-13-12.psd>[4][2][5]

生：我畫了數位圖。

<E：＼2023田田＼7-20＼遼寧教育·教研版202407＼LJ24-13-13.psd>

生：我是用豎式計算的，[ 3 7 1+ 1 5 4 4 2 5]。

師：仔細觀察，你有什么發現？

生：相同計數單位上的數相加。

生：哪一位滿“十”，就要向前一位進“1”。

生：通過方塊圖和數位圖可以清楚地看出，十位滿十向百位進“1”的過程。

師：整數加法是把相同計數單位上的數相加。這個過程可以寫成371 + 54 = 3（百） + 7（十） + 1（一） + 5（十） + 4（一） = 3（百） + （7 + 5）（十） + （1 + 4）（一） = 3（百） + 1（百） + 2（十） + 5（一） = 425。

加法算理是最基礎的算理，是四則運算以及其他所有運算的啟蒙，對加法算理的理解在學生的整個運算中起著至關重要的作用。很多教師在教學中對計數比較重視，突出講解，但在計算中卻弱化了對計數單位的關注。在教學“數概念”與“數運算”兩個內容時，很多教師存在“脫節”現象，多數計算教學會停留在運算技能上，采用豎式，按計算法則一位一位地相加，最后導致一部分學生只能快速計算出結果，卻不清楚算理。因此，在階段整理復習時，教師可以進行梳理，引導學生發現多位數加法和計數道理一樣，仍然先計算分別有多少個計數單位，再通過“十進制”的計數原理得出結果。這既是對學習經驗的激活，又是對前期存在的短板進行彌補。

（三）整數減法：關注逆向思維邏輯的進階式生長

減法是加法的逆運算，教師可以引導學生把研究整數加法的方法結構遷移運用到整數減法算理學習中。數學學習不僅要把每一類的學習方法研究透，還要把各種方法之間的關聯之處提煉出來。

師：計算“371 - 54”，用多種方式表示思考過程。

生：我用了四種方法（見下頁圖）。

師：觀察這幾種方法，你又有什么發現？

生：只有相同數位計數單位相同，才可以相減。

生：不夠減時要從前一位退“1”，然后在本位加10后再減。

師：和加法相比，它們有什么共同點？

生：也是只有相同的計數單位才能計算。

師：計算過程可以寫成371 - 54 = 3（百） + 7（十） + 1（一） - 5（十） - 4（一） = 3（百） + （6 - 5）（十） + （11 - 4）（一） = 3（百） + 1（十） + 7（一） = 317。

教師引導學生用可視化的方法表達加、減法的算理：相同的計數單位相加減。抽象的計數單位如實物一樣有“形”可依，學生在計算過程中只有在腦中抽象出每個計數單位對應的數學模型，才能克服“數”與“運算”的割裂現象，有效實現“數”與“運算”的一致性。在多種圖式的表達中，教師要引導學生特別重視方塊圖的掌握與應用。通過方塊圖，學生能從視覺“形”上感受到“單位相同”，不同計數單位有大小之分，是“一類”的才能相加，同時也是后續小數與分數算理研究的關鍵數學模型，便于演繹整數、小數、分數之間算f01d5d342a0d93baad4a55100fe93418理和算法的一致性。數位圖類似于計數器，但優于計數器，計數器每位受10顆珠的限制，數位圖可以任意畫○的個數，借助方塊圖，溝通數位圖和豎式之間的聯系，最后形成規范的豎式，進行抽象的數學符號表達。

二、探究乘法計算與乘積計數單位的二維變化規律

乘法是加法的簡便運算。整數乘法的算理，在教材中一般是通過實物情境進行研究的，用數學模型來解釋的例子較少。因為教材中沒有樣例，所以教師教學時操作起來很困難，容易忽略對乘法算理的探究，直接教給學生計算步驟。如果要體現與整數加、減法算理的一致性，教師不妨也引導學生借助方塊圖表達算理思路，感受其比數位圖有明顯的優勢。

（一）多位數乘法算理分享與圖譜模型構建

教師要引導學生在計算中對照實物與圖形，歸納出具有代表性的乘法數學模型。下面以“三位數乘兩位數”為例來闡述。

師：請大家計算“12 × 128”，并用自己喜歡的方式表達思考過程。

生：我用口算128×10 = 1280，128 × 2 = 256，1280 + 256 = 1536。

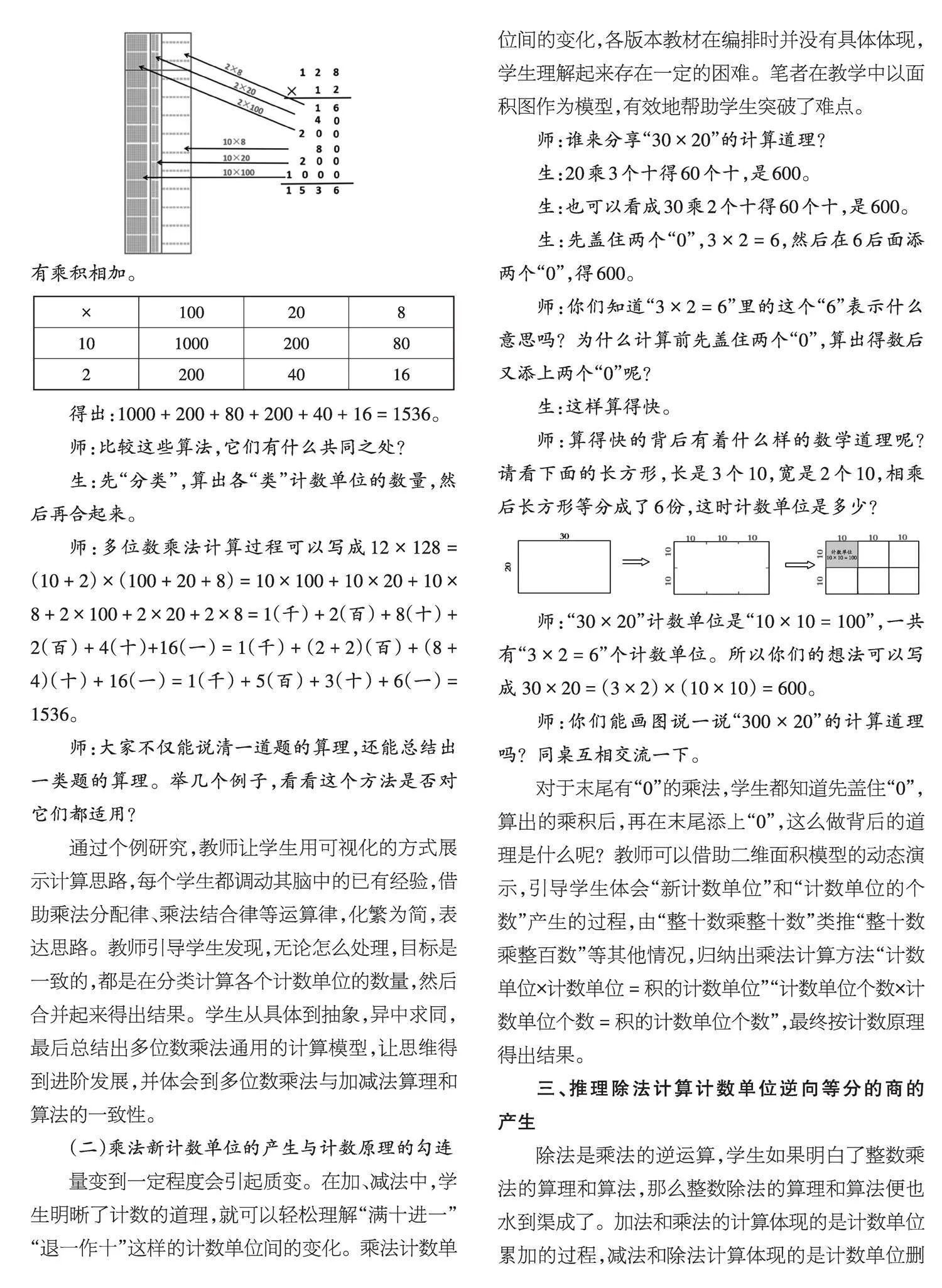
生：個位“8”乘12得96個一；十位“2”乘12得24個十；百位“1”乘12得12個百；最后三積相加得1536。

<E：＼2023田田＼7-20＼遼寧教育·教研版202407＼LJ24-13-18.psd>

生：我是用三位數乘兩位數，這樣更簡便。個位“2”乘128得256個一；十位“1”乘128得128個十；然后兩積相加結果也是1536。

<E：＼2023田田＼7-20＼遼寧教育·教研版202407＼LJ24-13-19.psd>

生：把這兩個分步過程疊放在一起，可以看出每一步的計算過程。

<E：＼2023田田＼7-20＼遼寧教育·教研版202407＼LJ24-13-20.psd>

師：他的方法還可以做成“面圖譜”。

生：還可以用表格表示出任意的兩個多位整數相乘的方法，把兩個乘數分別按計數單位拆分，列成表格，把兩兩相乘的積記錄在相交的格里，最后把所有乘積相加。

[× 100 20 8 10 1000 200 80 2 200 40 16 ]

得出：1000 + 200 + 80 + 200 + 40 + 16 = 1536。

師：比較這些算法，它們有什么共同之處？

生：先“分類”，算出各“類”計數單位的數量，然后再合起來。

師：多位數乘法計算過程可以寫成12 × 128 = （10 + 2） × （100 + 20 + 8） = 10 × 100 + 10 × 20 + 10 × 8 + 2 × 100 + 2 × 20 + 2 × 8 = 1（千） + 2（百） + 8（十） + 2（百） + 4（十）+16（一） = 1（千） + （2 + 2）（百） + （8 + 4）（十） + 16（一） = 1（千） + 5（百） + 3（十） + 6（一） = 1536。

師：大家不僅能說清一道題的算理，還能總結出一類題的算理。舉幾個例子，看看這個方法是否對它們都適用？

通過個例研究，教師讓學生用可視化的方式展示計算思路，每個學生都調動其腦中的已有經驗，借助乘法分配律、乘法結合律等運算律，化繁為簡，表達思路。教師引導學生發現，無論怎么處理，目標是一致的，都是在分類計算各個計數單位的數量，然后合并起來得出結果。學生從具體到抽象，異中求同，最后總結出多位數乘法通用的計算模型，讓思維得到進階發展，并體會到多位數乘法與加減法算理和算法的一致性。

（二）乘法新計數單位的產生與計數原理的勾連

量變到一定程度會引起質變。在加、減法中，學生明晰了計數的道理，就可以輕松理解“滿十進一”“退一作十”這樣的計數單位間的變化。乘法計數單位間的變化，各版本教材在編排時并沒有具體體現，學生理解起來存在一定的困難。筆者在教學中以面積圖作為模型，有效地幫助學生突破了難點。

師：誰來分享“30 × 20”的計算道理？

生：20乘3個十得60個十，是600。

生：也可以看成30乘2個十得60個十，是600。

生：先蓋住兩個“0”，3 × 2 = 6，然后在6后面添兩個“0”，得600。

師：你們知道“3 × 2 = 6”里的這個“6”表示什么意思嗎？為什么計算前先蓋住兩個“0”，算出得數后又添上兩個“0”呢？

生：這樣算得快。

師：算得快的背后有著什么樣的數學道理呢？請看下面的長方形，長是3個10，寬是2個10，相乘后長方形等分成了6份，這時計數單位是多少？

<E：＼2023田田＼7-20＼遼寧教育·教研版202407＼LJ24-13-2.psd>[計數單位

10 × 10 = 100]

師：“30 × 20”計數單位是“10 × 10 = 100”，一共有“3 × 2 = 6”個計數單位。所以你們的想法可以寫成 30 × 20 = （3 × 2） × （10 × 10） = 600。

師：你們能畫圖說一說“300 × 20”的計算道理嗎？同桌互相交流一下。

對于末尾有“0”的乘法，學生都知道先蓋住“0”，算出的乘積后，再在末尾添上“0”，這么做背后的道理是什么呢？教師可以借助二維面積模型的動態演示，引導學生體會“新計數單位”和“計數單位的個數”產生的過程，由“整十數乘整十數”類推“整十數乘整百數”等其他情況，歸納出乘法計算方法“計數單位×計數單位 = 積的計數單位”“計數單位個數×計數單位個數 = 積的計數單位個數”，最終按計數原理得出結果。

三、推理除法計算計數單位逆向等分的商的產生

除法是乘法的逆運算，學生如果明白了整數乘法的算理和算法，那么整數除法的算理和算法便也水到渠成了。加法和乘法的計算體現的是計數單位累加的過程，減法和除法計算體現的是計數單位刪減的過程。

（一）三位數除以一位數算理探究

例如，有437本課外書平均分給3個班，每個班能分到多少本？還多出幾本？

師：誰來說一說你的思考過程？

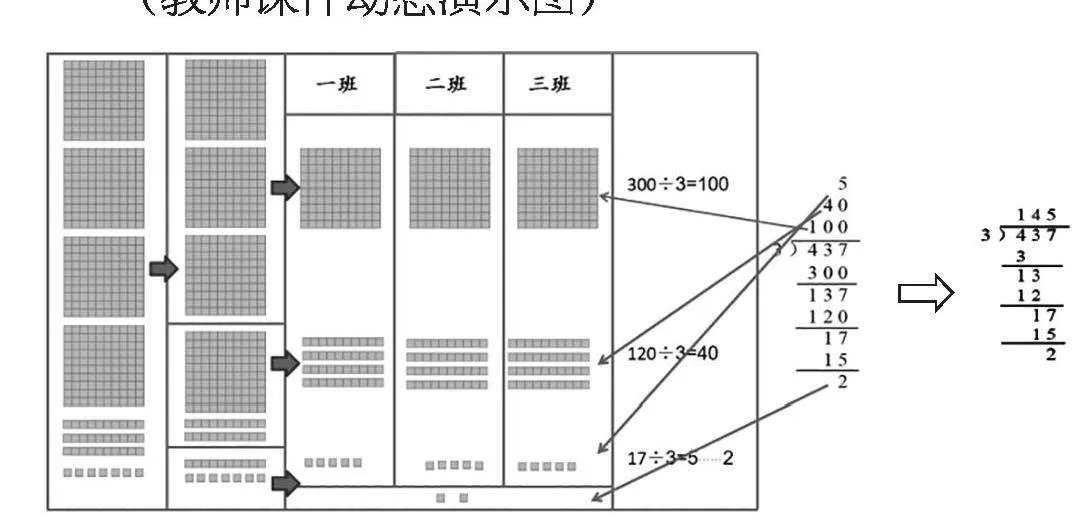
生：我用口算的方法，因為300 ÷ 3 = 100，120 ÷ 3 = 40，15 ÷ 3 = 5，17 - 15 = 2，所以437 ÷ 3 = 145……2。

生：我用分小方塊圖的方法來計算。

（教師課件動態演示圖）

<E：＼2023田田＼7-20＼遼寧教育·教研版202407＼LJ24-13-22.psd><E：＼2023田田＼7-20＼遼寧教育·教研版202407＼LJ24-13-23.psd>

師：這個過程可以用這樣的豎式表示出來。會簡寫這個豎式嗎？請對照圖說說理由。

生：因為3個百除以3得1個百，商1寫在百位上表示的就是1個百，后面2個0可以省略不寫。

生：分哪個計數單位，商就寫在哪一位上面，不會亂。

生：12個十除以3得4個十，十位商4，個位0也可以省略。

師：現在理解為什么“除到哪一位，商就寫在哪一位的上面”了吧。每個數位的數都有相應的“位值”，豎式中每次商與除數的乘積，末尾的“0”都可以省略不寫。

師：除法計算，就是在等分計算單位。請把這個過程用算式表示出來。

生：437 ÷ 3 = 4（百）3（十）7（一） ÷ 3 = 3（百） ÷ 3 + 12（十） ÷ 3 + 17（一） ÷ 3 = 145……2。

（二）除法新計數單位的產生與計數原理的勾連

除法中新計數單位的產生是學生最難理解的一個知識點，教師仍可以引導學生借助面積模型，在乘法的基礎上進行倒推。結合班級的學情，學生若能基于nWCjMWva/X3JGHStfLVnhg==乘法算理完成推理，教師可放手讓其自主探究分享；若有難度，教師可用課件演示，以便把此推理邏輯運用到小數和分數的算理和算法一致性研究中。

師：誰來分享一下“12000 ÷ 30”的思考過程？

生：被除數12000可以看成長方形的面積，除數30可以看成長方形的寬，12000 ÷ 30是求長方形的長。“30”里有3個10，把寬等分成3份，每份長方形面積是4000；4000里有4個千，把它等分成4份，每份小長形的面積是1000；聚焦每個小長方形，寬是10，則長為1000 ÷ 10 = 100，是長的計數單位；長為4個百，即400。

生：剛才這個過程可以用算式表示為12000 ÷ 30 = （12 ÷ 3） × （1000 ÷ 10） = 4 × 100 = 400。

生：我發現“計數單位 ÷ 計數單位 = 商的計數單位”“計數單位個數 ÷ 計數單位個數 = 商的計數單位個數”，然后“新的計數單位 × 計數單位個數 = 商”。

學生在操作均分小方塊時，能不斷強化各種計數單位的數學模型，讓抽象的計數單位和生活中的物品一樣“有形可依”，讓復雜的計算過程“有理可講”。通過推理，學生發現除法的最終計算方法也是在計算各有多少個計數單位，最后再合并。

綜上所述，整數的加、減、乘、除的算法是一致的：計數單位的個數 × 計數單位；算理也是一致的：通過運算律可以推理出算理。加法是四則運算的核心，減法是加法的逆運算，乘法是加法的簡便運算，除法是乘法的逆運算，是減法的簡便運算。學生親歷操作，結合課件的動態演示，“數”“形”結合，成功打通“數概念”與“數運算”之間的“隔斷墻”，深刻體會整數四則運算的一致性。

參考文獻：

［1］于玲.打通“隔斷墻”，落實“數的運算”的一致性［J］.小學數學教師，2023（7～8）.

［2］鞏子坤，史寧中，張丹.義務教育數學課程標準修訂的新視角：數的概念與運算的一致性［J］.課程·教材·教法，2023（7）.

（責任編輯：楊強）