借助開放式題型提高初中生數學解題能力


【摘要】初中數學解題教學中,培養學生解題能力是非常重要的內容.而在培養學生解題能力的過程中,培養學生解題思維能力是非常重要的.開放式題型具有明顯的探索性質,能夠有效激發學生的探索興趣,從而激發學生的思維,實現對學生的解題能力進行更好的培養.本文通過開放式例題對初中解題教學中提升學生解題能力的策略進行說明.
【關鍵詞】初中數學;解題教學;開放題型
開放式題型是相對閉合式題型而言的,開放式題型存在條件不完整或者結論不完整的情況,從而形成條件開放、結論開放或者策略開放的情況.同時,開放式題型解題過程中需要學生充分應用所學的數學知識和數學思想方法進行問題的觀察、對比分析,從而得到結論,更加注重學生分析問題和解決問題的能力,所以通過開放式題型進行解題教學對提升學生解題能力有非常重要的作用.
1 以條件探索型開放式題型提升學生的解題認識
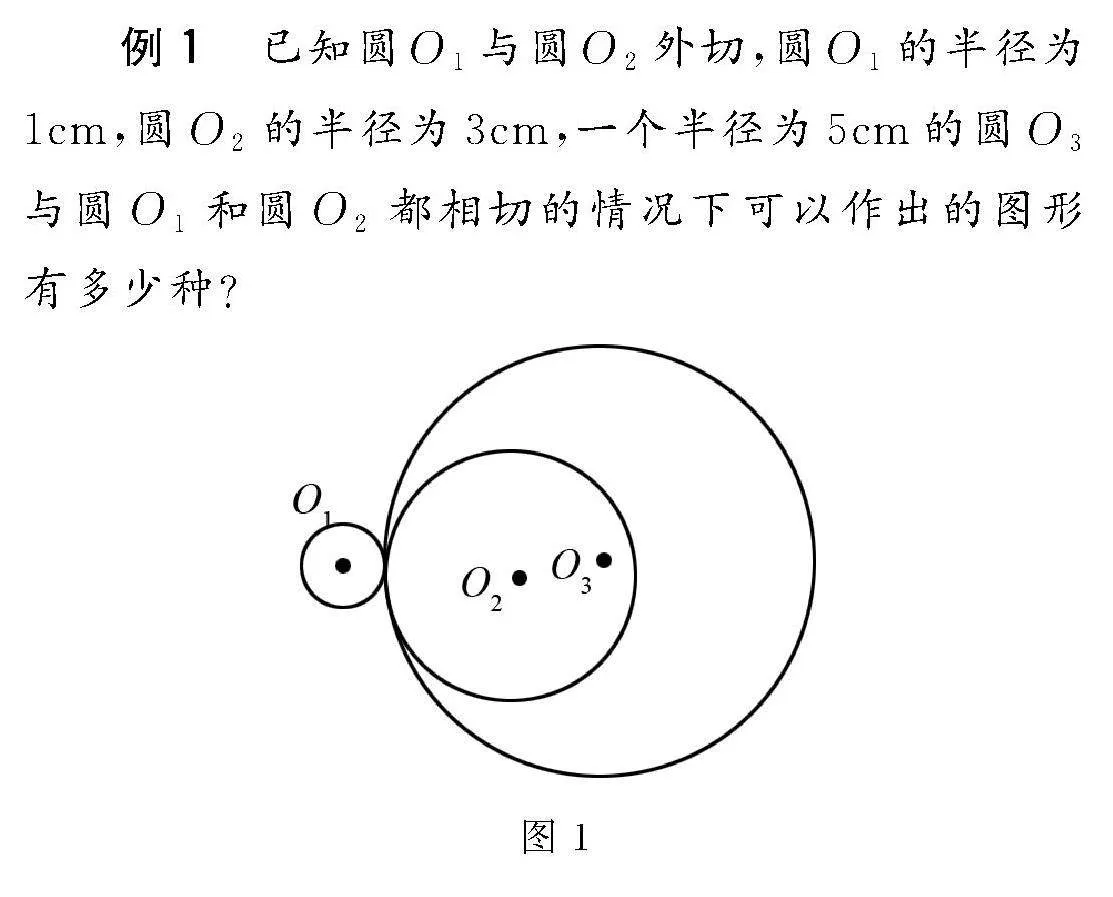
例1 已知圓O1與圓O2外切,圓O1的半徑為1cm,圓O2的半徑為3cm,一個半徑為5cm的圓O3與圓O1和圓O2都相切的情況下可以作出的圖形有多少種?
圖1
分析 本題對圓O3與圓O1和圓O2相切的情況并沒有進行明確,所以在解題過程中就需要對圓O3分別和圓O1、圓O2屬于內切還是外切進行討論.當圓O3與圓O1、圓O2都是內切的情況時,因為圓O1的半徑為1cm,8b9e5348406e216781dc551f3bfd489a圓O2的半徑為3cm,兩個圓的半徑之和小于圓O3的半徑,所以會形成兩種圖形;當圓O3與圓O1、圓O2都是外切的情況下,也會形成兩種外切的圖形;當圓O3與圓O1內切,與圓O2外切,則會形成1種圖形,同理當圓O3與圓O2內切,與圓O1外切也會形成一種圖形,所以通過對上述不同相切方式形成的圖形進行統計,圓O3與圓O1和圓O2都相切的情況有6種.如圖2所示.
圖2
通過條件探索型開放式題型來對學生進行解題教學,可以讓學生更加深刻地理解解題條件在解題中的重要作用,從而讓學生明確初中數學解題就是根據已知條件來進行相關問題求解的過程,讓學生對解題有更加準確的認識,掌握解題的內涵,實現提升學生的解題能力.
2 以結論探索型開放式題型來培養學生解題思維的靈活性
例2 閱讀問題(1)的解答過程,然后進行問題(2)的解答.
(1)已知實數a,b滿足a2=2-2a,b2=2-2b,且a≠b,求ab+ba.
解法1 由a2=2-2a,b2=2-2b,
可得a2+2a-2=0,b2+2b-2=0,且a≠b,
所以可以將a,b作為方程x2+2x-2=0的兩個不相等的實數根,
根據韋達定理可知a+b=-2,ab=-2,
原式ab+ba=a2+b2ab=(a+b)2-2abab=(-2)2+4-2=-4.
解法2 將a2=2-2a,b2=2-2b兩式相減,
可得(a2-b2)+2(a-b)=0,
整理可得:(a-b)(a+b+2)=0.
因為a≠b,
所以a+b+2=0,解得a+b=-2.
將兩式相乘可得a2b2=(2-2a)(2-2b).
整理可得:(ab)2-4ab-12=0,
解得ab=6或ab=-2.
結合a+b=-2可知ab=6不成立,
所以a+b=-2,ab=-2.
原式ab+ba=a2+b2ab=(a+b)2-2abab=(-2)2+4-2=-4.
(2)已知實數p,q滿足p2-2p-5=0,5q2+2q-1=0,求p2+1q2.
分析 通過對(1)的兩種解題過程進行分析可以發現,解法1是通過構建一元二次方程的方式,通過韋達定理來進行問題的解決,相對于解法2更加簡單.同時通過對問題(1)和(2)進行對比發現(1)中的條件在(2)中沒有存在類似的條件,所以解題過程中需要對p≠1q與p=1q兩種情況進行分類討論.同時在解題過程中還需要對5q2+2q-1=0的格式進行調整,轉化為(1q)2-2×1q-5=0.
解 根據題意可知q≠0,
可以將5q2+2q-1=0轉化為(1q)2-2×1q-5=0,
當p≠1q時,可以將p,1q作為方程x2-2x-5=0的兩個不等實數根.
由韋達定理可得p·1q=-5,p+1q=2,
原式p2+1q2=(p+1q)2-2p·1q=22-2×(-5)=14.
當p=1q時,則p,1q為方程x2-2x-5=0的一個根,
所以p=1q=1±6.
原式p2+1q2=2p2=2(1±6)2=14±46.
顯然,這類結論探索型開放式問題中會存在較多的思維方式,不同的思維方式情況下會形成不同的解題思路,從而實現通過不同解題方式來進行問題的解決.教師在解題教學過程中可以通過這類試題來培養學生一題多解的能力,通過拓展學生解題思路的方式來進一步提升學生的解題能力.
3 結語
綜上所述,本文以初中數學中常見的條件探索型和結論探索型開放式題型的例題來對初中數學解題教學中通過開放型試題來提升學生的解題策略進行了說明.在解題教學中,通過條件探索型開放型試題能夠更加有效的提升學生對數學解題的認識,讓學生更好地掌握解題方法,而通過結論探索型開放型試題能夠有效激發學生的思維,從而通過不同方式來進行試題求解,通過兩種方式的有效結合,有效的提升了學生的解題能力.
參考文獻:
[1]鐘鋼.從培養思維能力的角度談初中數學開放題型教學[J].文理導航(中旬),2014(07):24.
[2]徐紀兵.巧妙設計,用開放型題培養思維能力[J].文理導航(中旬),2014(09):17.
[3]曹廣軍.淺析初中數學開放性問題[J].讀與寫(上,下旬),2014(21):210.

